扶壁式挡土墙控制工况探讨

丁 燕，高徐军，葛苗苗,韩文斌

(1.中国电建集团西北勘测设计研究院有限公司,西安 710065；2.西安理工大学 岩土工程研究所,西安 710048)

文章编号：1006—2610(2015)02—0037—07

扶壁式挡土墙控制工况探讨

丁 燕1，高徐军1，葛苗苗2,韩文斌1

(1.中国电建集团西北勘测设计研究院有限公司,西安 710065；2.西安理工大学 岩土工程研究所,西安 710048)

以汉江白河县城防洪工程扶壁式挡土墙不同的填土高度为研究对象，采用理正岩土计算软件和ANSYS三维有限元分析软件，计算扶壁式挡土墙在各工况下的安全系数和应力变化，并引入水位降幅比，分析了水位骤降工况下扶壁式挡土墙的稳定性和受力状态，综合稳定性和受力状态2个因素对挡土墙的影响，判断扶壁式挡土墙的控制工况。计算结果表明，扶壁式挡土墙的控制工况与其墙后填土高度有关，当墙后填土高度和挡土墙高度相同时，其控制工况为水位骤降工况；挡土墙顶部出现悬臂段，挡土墙的稳定性较好，墙前高水位条件下，墙体拉应力急剧增大，挡土墙的控制工况为校核洪水位工况。可以此确定水工挡土墙工程控制工况。

扶壁式挡土墙；水位骤降；安全系数；控制工况；拉应力

0 前 言

扶壁式挡土墙是一种钢筋混凝土薄壁式挡土结构，其主要特点是构造简单、施工方便，墙身断面较小，自身质量轻，可以较好地发挥材料的强度性能，能适应承载力较低的地基且整体稳定性好，因此除了被应用于公路边坡和大型边坡治理外，更被广泛应用于水利工程中。通常，水工挡土墙的设计不仅要满足规范要求，还必须满足稳定性和受力要求，因此，必须以水工挡土墙在各种工况下的稳定性和受力状态判断其控制工况，根据控制工况的稳定性和受力状态校正设计。SL 379-2007《水工挡土墙设计规范》[1]中已明确挡土墙的设计标准和稳定性计算方法，也有不少文献[2-6]对挡土墙的稳定性和受力进行了分析。由于水工挡土墙荷载计算复杂，尤其是水位骤降工况下最不利水深难以确定，所以针对水工挡土墙控制工况的研究很少，文献[7]认为水位骤降速度越快，堤岸的稳定性降低越大，同一水位骤降速度，水位越低堤岸稳定性越差。文献[8]对挡土墙在水位骤降工况下的不利水深进行了研究，认为汛期水位骤降情况下，挡土墙稳定性不利水深不一定是墙前和墙后初始最大水深的组合，而可能是墙前水位降落过程中的某一过程水深。文献[9-11]对挡土墙或岸坡堤防在水位骤降工况下的稳定性也进行了研究，但目前大多数文献对挡土墙的稳定性和受力都取单一工况进行研究，并且很少综合挡土墙的受力和稳定性来确定挡土墙的控制工况。本文即是针对这一问题，以陕西汉江白河县不同填土高度的扶壁式挡土墙为实例，结合理正设计软件及ANSYS三维有限元仿真软件，计算水工扶壁式挡土墙在不同工况的荷载组合下，挡土墙的稳定安全系数和拉应力大小，结合挡土墙的稳定性和受力情况，综合判断扶壁式挡土墙的控制工况。

1 工程案例分析

1.1 工程概况

图1 工程场址示意图

汉江白河县防洪工程是一个城市防洪为主，兼顾市政景观及G316过境交通的综合工程，堤线全长约3 849 m。防洪工程范围内属低山地貌，区内地形切割强烈，河谷蜿蜒曲折，两岸基岩裸露，山坡陡峻。堤防工程区汉江河流基本顺直，基岩高出河床50～100余m，堤防工程位于汉江和白石河高、低漫滩之上，沿堤线均有地下水分布，属孔隙性潜水类型，一般情况下堤线地下水位埋深在1.0～1.5 m之间(见图1)。经计算，水流平行坡岸时冲刷深度为2.72 m。该工程堤防建筑物级别为4级，由于地势特殊，该工程扶壁式挡土墙最高达28.0 m。

1.2 相关参数及物理力学指标

本文根据水利行业挡土墙规范SL 379-2007《水工挡土墙设计规范》[1]及该工程挡土墙级别将其抗滑稳定安全系数和抗倾覆稳定安全系数的标准值分别取为1.30和1.50；根据SL 191-2008《水工混凝土结构设计规范》[12]，土压力分项系数取1.2，永久荷载对结构有利时，取荷载组合系数为0.95。理正设计软件分析相关参数见表1，ANSYS三维计算物理力学参数见表2。

表1 理正设计软件分析相关参数表

表2 ANSYS三维数值计算力学参数表

1.3 分析断面及三维模型

该工程墙前最高水位为校核洪水位，和挡墙墙高相同，墙后水位高程为填土高程，墙后最大水深即为填土高度，由于墙后填土高度的变化导致部分区段扶壁式挡土墙顶部会出现较大悬臂段，本文选取2个典型剖面进行分析，具体设计尺寸如图2。

三维计算模型在图2分析断面的基础上，选择2个分缝间14.9 m的长度进行建模，对应模型网格见图3、4。考虑到计算工况的复杂性，将挡土墙结构单元和基岩材料都采用实体单元(SOLID45单元)进行模拟，选取Drucker-Prager屈服准则作为收敛准则，计算过程中模型四周法向约束、底部固定约束。

图2 理正分析辅助断面 单位：m

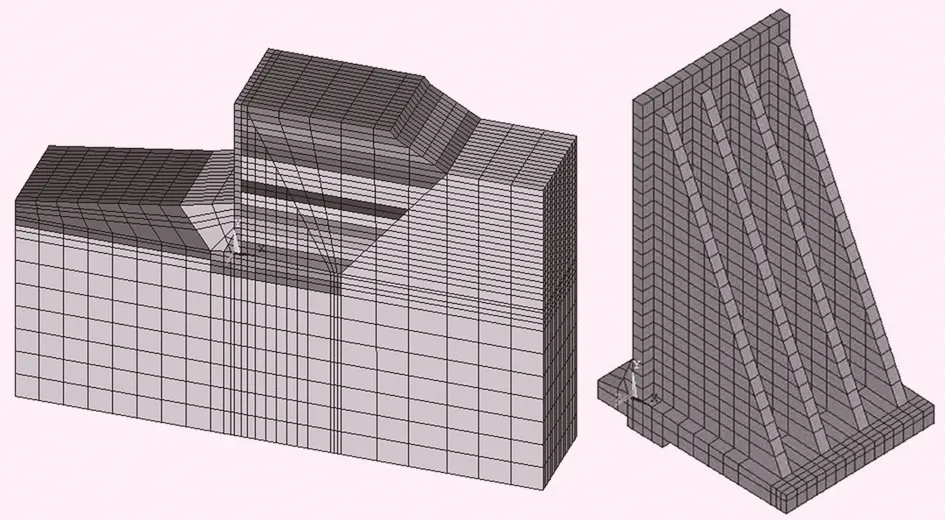
图3 断面1三维计算模型网格图

图4 断面2三维计算模型网格图

2 工况及荷载计算

2.1 荷载工况组合

本文分析了汉江扶壁式挡土墙在施工、完建、正常运行、设计洪水位、校核洪水位及水位骤降工况下的稳定性和受力情况， 各工况下主要的作用荷载包括：挡土墙自重、洪水水压力荷载、水浮力荷载、土压力荷载、汽车荷载、人群荷载。由于工程完建后稳定水位较低，且工程区抗震设防烈度为6度，故不考虑风浪荷载及地震荷载，风荷载及雪荷载等作用较小，也不予以考虑。

根据以上基本组合和特殊组合，将计算工况考虑的荷载总结如下。

(1) 施工期工况：挡土墙结构自重+附加荷载(碾压水平挤出荷载)+主动土压力。

(2) 完建工况：挡土墙结构自重+主动土压力+静水压力+扬压力+公路汽车荷载。

(3) 正常挡水位工况：挡土墙结构自重+主动土压力+水重+静水压力+扬压力+公路汽车、行人荷载。

(4) 设计洪水位工况：挡土墙结构自重+主动土压力+水重+静水压力+扬压力+公路汽车、行人荷载。

(5) 校核洪水位工况：挡土墙结构自重+主动土压力+水重+静水压力+扬压力+公路汽车、行人荷载。

(6) 墙前洪水位骤降工况：挡土墙结构自重+主动土压力+水重+静水压力+扬压力+公路汽车、行人荷载。

根据工程所在地水文地质环境，除施工及墙前洪水位骤降工况外，其他工况下墙前墙后水深如表3所示，其中水深从挡土墙底板算起。

2.2 特殊荷载计算及施工模拟

本文静水压力和扬压力按照DL5077-1997《水工建筑物荷载设计规范》[12]计算，三维计算采用有梯度的均布荷载模拟，如图5所示。根据JTG D30-2004《公路路基设计规范》[13]，将车辆荷载作用在挡土墙背填土上所引起的附加土体侧压力，按公式(1)换算成等代均布土层厚度计算：

(1)

式中：h0为换算土层厚度，m；γ为墙背填土重度，kN/m3；q为车辆荷载附加荷载强度，墙高小于2 m，取20 kN/m2；墙高大于2 m，取10 kN/m2；墙高在2～10 m之间时，附加荷载强度用直线内插法计算。作用于墙顶或墙后填土上的人群荷载强度规定为3 kN/m2。

表3 各工况下研究断面墙前墙后水深表 /m

考虑到实际施工情况，三维计算施工过程模拟步骤为：① 挡土墙地基及边坡开挖→② 施做片石混凝土垫层→③ 分层(2～3 m)浇筑挡土墙及扶壁并回填墙后填土→④ 回填墙内侧填土直至与墙外侧地面等高度时回填墙外侧填土，提供反压和坡脚

防冲刷措施，保证墙踵板及墙面板内外受力均匀→⑤ 分层(2～3 m)浇筑挡土墙及扶壁并填筑墙后土层直至设计高程。主要施工步骤如图6。

图5 静水压力及扬压力计算方法示意图

图6 三维分析主要施工步骤示意图

3 洪水骤降工况下不利水深的确定

3.1 水位降幅比概述

一般说来，墙前水位的降落速度与挡墙所在河段河道形态和河床或行洪通道纵坡陡缓有关，而墙后地下水位的降落速度与挡土墙排水设施(如墙身排水孔，墙背排水管或排水盲沟等)和墙后土层物理特性及排水效果有关，还有可能受到墙前水位顶托的影响，工程运行多年后如果部分排水孔堵塞或反滤材料孔隙淤塞而造成排水效果不良，会减缓墙后地下水位的降速。因而某些工程的墙后水位降落速度比墙前要慢一些，由于墙前洪水位和墙后土层地下水位降落是有关联的，故有必要引入挡土墙墙前墙后水位降幅比n[7]，其定义是：设某一时间段内墙前墙后水位下降高度分别为ΔHq、ΔHh，则n即为前者与后者的比值，即有表达式：

(2)

显然，n的值越大，墙前水位降落速度越快，反之亦然。当n=1时，即表示此段时间内墙前水位和墙后水位差不变；若n>1，则表示此段时间内墙前水位降速较墙后水位降速快。这样，不同的水位降比n就能模拟不同因素影响下墙前墙后的水位降落关系。

3.2 不利水深确定

本文分析了挡土墙在不同n值下，2个研究断面墙前水深从最大值(校核洪水位)降至0的过程中挡土墙的稳定性，得到稳定安全系数和墙前水深关系如图7、8，由图可见：所有水位降比n值曲线的抗滑移稳定安全系数Kc和抗倾覆稳定安全系数Ko随着墙前水深Hq的降低均呈现先减小后增大的趋势，这表明在墙前水位降落过程中，对扶壁式挡土墙稳定性不利的水深是水位降落过程中的某一过程水深；同理，通过ANSYS三维计算不同n值下水位动态变化中挡土墙的拉应力，由图9拉应力和墙前水深关系可得，扶壁式挡土墙受拉不利水深也为水位骤降过程中某一不利水深。不同的是断面2由于挡土墙顶部有6 m的悬臂段，所以在墙前水位很高时，挡土墙在悬臂端根部受到很大拉应力，随着墙前水位降低，断面2的σ1～Hq与断面1相同，呈现先增大后减小的趋势。

通过计算分析，本文进一步证明了文献[8]的结论，在墙前水位骤降过程中，对挡土墙稳定性和受力不利的水深是水位降落过程中的某一过程水深，而不是墙前最大水深和墙后最大水深的组合。

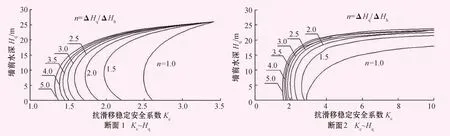
图7 Kc～ Hq关系曲线图

图8 Ko～ Hq关系曲线图

图9 σ1～Hq关系曲线图

一般根据挡土墙墙前河段所处的水文环境，来确定墙前墙后的水位降幅比值n，表4是文献[8]给出的不同水文环境下n的建议值。本工程项目地处陕南山区，洪水位降速较快，墙前墙后水位降幅比n可取1.5～3.0，由于本文挡土墙高达28 m,考虑安全储备，取n=3.0计算断面1和断面2在洪水位骤降工况下的不利水深，计算结果见表5。

表4 不同水文环境下水位降幅比n取值范围表

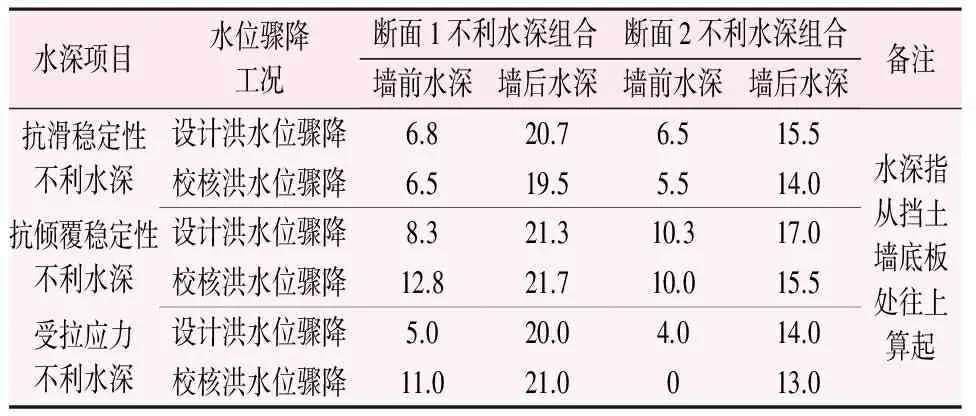
表5 n=3时水位骤降过程中墙前墙后不利水深表 /m

4 计算结果分析

4.1 理正二维稳定性计算结果分析

表6是理正设计软件计算研究对象在各工况下的稳定安全系数，从表6可以看出：

(1) 各工况下挡土墙的稳定安全系数均满足规范要求，由于断面2挡土墙高度较高，墙后填土高度较低，在挡土墙顶部出现6 m高的悬臂段，在洪水位作用下，挡土墙临河一侧受很大的水压力，很难发生滑移或倾覆，因此设计洪水位和校核洪水位下稳定安全系数很大。

(2) 水工扶壁式挡土墙高度越大，稳定性不一定就差，这和墙后填土高度有关，断面2挡墙高度虽然比断面1大，但稳定性较断面1好，这是由于断面2的墙后填土高度较低，洪水来临或者退去时，在相等的水位降落速度下，断面2的墙前墙后水位差较小，其稳定性较好，稳定安全系数较大。

(3) 比较几个工况下挡土墙的稳定安全系数可得，断面1在设计洪水位骤降工况，抗滑移稳定安全系数Kc、抗倾覆稳定系数Ko最小，故断面1的稳定性控制工况为设计洪水位骤降工况，同理，断面2在正常运行时稳定安全系数最小，断面2的稳定性控制工况为正常运行工况。

4.2 扶壁式挡土墙三维受力分析

通过ANSYS计算各工况不同荷载组合下挡土墙的应力大小，结果如表7，从表中可以看出：

(1) 除了校核洪水位工况，其他工况下两断面的拉应力均满足混凝土抗拉强度要求，且断面1整体拉应力较断面2大，这是因为断面1墙后填土高度大，主动土压力较大，导致挡土墙墙踵板所受拉应力较大。

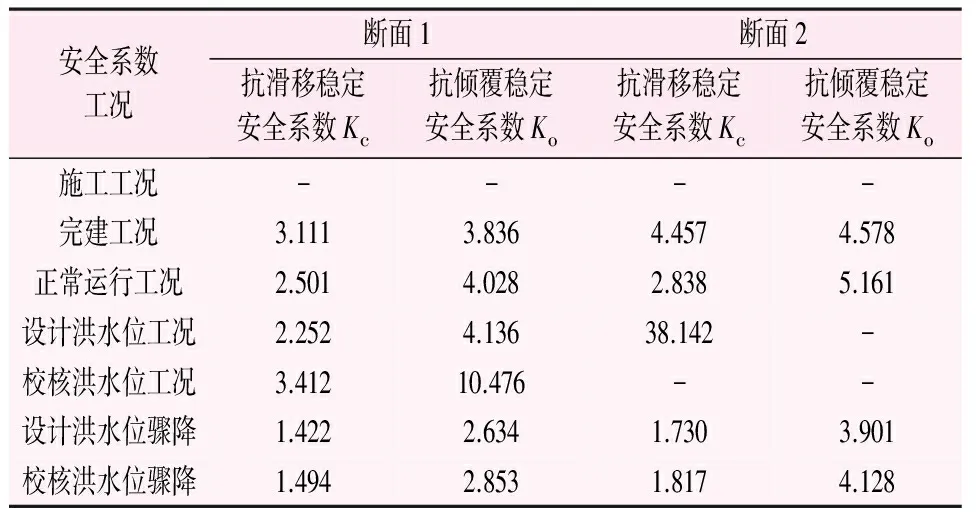
表6 各工况下研究断面稳定安全系数表

(2) 断面1在设计洪水位骤降工况下所受拉应力最大，为0.66 MPa，故断面1的控制工况为设计洪水位骤降工况；断面2在校核洪水位工况下拉应力最大，为2.04 MPa，故断面2的控制工况为校核洪水位工况，且拉应力超过了C40混凝土的设计抗拉强度值1.65 MPa，这是因为断面2挡土墙顶端有6 m的悬臂端，当墙前水位大于墙后填土高度时，在悬臂端根部就会出现较大拉应力，而且水位越高，拉应力越大。

表7 各工况下研究断面拉应力值表

本文所研究的2个断面，由于其填土高度的不同，导致其最大拉应力出现的位置也不一样，断面1填土高度和挡土墙高度相等，墙后主动土压力较大，各工况下最大拉应力均出现在墙踵板端部，在水位骤降工况下，由于墙前墙后水位差增大，扶壁中部也出现较大拉应力，如图10所示。断面2各工况拉应力出现的位置同断面1大致相同，不同的是由于断面2墙顶有6 m的悬臂段，在校核洪水位工况下，最大拉应力出现在悬臂段根部，且拉应力超过了混凝土抗拉强度，具体如图10所示。

图10 三维计算最大拉应力云图

5 控制工况探讨

目前大部分水工挡土墙工程将水位骤降工况作为最危险工况，从本文的分析中可知：水位骤降工况并不一定是控制工况，并且挡土墙的控制工况不能仅仅从稳定性角度分析，挡土墙可能在某一工况下稳定性很好，但是受力远远超过了设计要求，所以应当结合挡土墙的稳定性和受力情况综合分析，来确定挡土墙的控制工况。

从本文的分析可以看出，挡土墙的稳定性和受力与挡土墙的墙后填土高度有关。墙后填土高度和挡土墙高度相同时(如断面1)，其受力在各工况下均比较稳定，拉应力变化范围较小，反而，由于墙后填土高度和挡土墙高度相差不大，其在水位骤降工况下稳定性最差，因此，此种断面形式的水工扶壁式挡土墙，可以通过稳定性评价来确定其控制工况，且通过本文分析可得，其控制工况为水位骤降工况。墙后填土高度低于挡土墙高度时，挡土墙顶部有悬臂端(如断面2)，这种情况下，墙后的主动土压力较小，由于墙前水位相对较高，所以稳定性相对较好，尤其是在设计或校核洪水位时，稳定安全系数很大，且悬臂段越高，安全系数越大，挡土墙越稳定。但这种断面形式下，悬臂段根部会在墙前高水位时出现很大拉应力，甚至超过混凝土的设计抗拉强度，因此当挡土墙顶部有悬臂段时，挡土墙的受力条件成为判断控制工况的依据，挡土墙的控制工况为墙前水位最高的工况，多为校核洪水位。对于在墙前高水位下挡土墙悬臂段根部出现较大拉应力的情况，应当采取相应的构造措施或加大配筋。

6 结 语

通过结合理正设计软件和ANSYS三维有限元仿真软件分析2种不同断面的扶壁式挡土墙，在施工工况、完建工况、正常运行工况、校核洪水位工况、设计洪水位工况以及水位骤降工况下的稳定性和受力情况，得到扶壁式挡土墙以下结论：

(1) 汛期水位骤降情况下，扶壁式挡土墙稳定性不利水深和受力不利水深不一定是墙前和墙后初始最大水深的组合，而可能是墙前水位降落过程中的某一过程水深。

(2) 水位骤降工况并不一定是控制工况，挡土墙可能在某一工况下稳定性很好，但是受力远远超过了设计要求，故扶壁式挡土墙的控制工况应当综合稳定性和受力2个影响因素来确定。

(3) 扶壁式挡土墙的控制工况与其墙后填土高度有关，当墙后填土高度和挡土墙高度相同时，稳定性为其控制工况判断依据，此时控制工况为水位骤降工况；当墙后填土高度低于挡土墙高度，挡土墙顶部出现悬臂段时，挡土墙稳定很好，所受拉应力较大，受力条件决定其控制工况，此时控制工况为校核洪水位工况。

本文所获得的结论及计算方法对水工挡土墙工程控制工况的确定有一定的参考价值。

[1] SL379-2007,水工挡土墙设计规范[S].北京：中国水利水电出版社，2008.

[2] 谢新宇,杨相如,刘开富,等.水位变化对带挡土墙路基稳定性影响[J].地下空间与工程学报, 2009,5(6):1262-1271.

[3] 周雪峰,李江新,魏伟. 套打树根桩的重力式挡土墙设计[J].地下空间与工程学报, 2007,3(8):1426-1429.

[4] 郑颖人,时卫民,孔位学.库水位下降时渗透力及地下水浸润线的计算[J].岩石力学与工程学报，2004，23(18)：3203-3210.

[5] Lane P A, Griffiths D V. Assessment of stability of slopes under drawdown conditions[J].Journal of geotechnical and geoenvironmental engineering, 2000, 126(5): 443-450.

[6] 张文杰, 陈云敏, 凌道盛. 库岸边坡渗流及稳定性分析[J].水利学报，2005，36(12)：1510-1515.

[7] 赵宇坤,刘汉东,李庆安. 洪水浸泡和水位骤降情况下黄河下游堤防堤岸稳定性分析[J].岩土力学，2011，32(5)：1495-1499.

[8] 何善国. 墙前水位骤降挡土墙稳定不利水深取值问题分析研究 [J].红水河，2012,31(2):34-41.

[8] 吴琼,唐辉明,王亮清. 库水位升降联合降雨作用下库岸边坡中的浸润线研究[J].岩土力学，2009，30(10)：3025-3031.

[10] 阙云. 浸水重力式挡土墙稳定性的最不利水位确定[J].福建建设科技，2012,(5):11-14 .

[11] 张敏江,赵乃志,杨军彩.浸水重力式挡土墙的滑移分析[J].沈阳建筑大学学报(自然科学版)，2005,(1):5-7.

[12] SL191-2008,水工混凝土结构设计规范[S].北京：中国水利水电出版社，2009.

[13] DL5077-1997,水工建筑物荷载设计规范 [S].北京：中国电力出版社，1998.

[14] JTG D30-2004,公路路基设计规范 [S].北京：人民交通出版社，2004.

Study on Control Conditions of Counterfort Retaining Wall

DING Yan1, GAO Xu-jun1, GE Miao-miao2, HAN Wen-bin1

(1. POWERCHINA Xibei Engineering Co., Ltd., Xi'an 710065, China;2. Geotechnical Engineering Institute, Xi'an University of Technology, Xi'an 710048, China)

With the different height of the backfilling soil of the counterfort retaining wall in the flood control project in Baihe County downtown as the study subject and by application of Lizheng geotechnical software and ANSYS 3D finite element software, safety factors and stress variation of the counterfort retaining wall at various conditions are calculated. Furthermore, the water level drop range ratio is introduced. stability and action of the counterfort retaining wall in condition of the water level prompt drop are analyzed accordingly. In consideration of impacts on the retaining wall by its general stability as action, the control condition of the counterfort retaining wall is judged. The calculation shows that the control condition of the counterfort retaining wall is related to the soil backfilling height. When the height of soil backfilling behind the retaining wall is the same as the retaining wall height, its control condition is the one of water level prompt drop. When the cantilever at the top of the retaining wall occurs, stability of the retaining wall is better. In condition of high water level before the retaining wall available, the tensile stress of the wall increases rapidly. The control condition of the retaining wall is the check flood level. Based on this, the control condition of the retaining wall can be determined.

counterfort retaining wall; water level prompt drop; safety factor; control condition; tensile stress

2014-12-10

丁燕(1961- )，女，西安市人，教授级高工，主要从事桥梁工程的设计与研究工作.

TU476.4

A

10.3969/j.issn.1006-2610.2015.02.010