滑坡三维破坏概率计算

汤罗圣, 颜廷舟, 邓长青, 岳 敏

(湖北省交通规划设计院, 湖北 武汉 430051)

滑坡三维破坏概率计算

汤罗圣, 颜廷舟, 邓长青, 岳 敏

(湖北省交通规划设计院, 湖北 武汉 430051)

摘要：[目的] 对滑坡的三维破坏概率进行计算和验证，为滑坡稳定性定量评价提供一种新思路。 [方法] 采用FLAC 3D数值模拟软件，运用Rosenblueth方法计算滑坡的三维破坏概率，将其计算结果与二维破坏概率进行对比研究。 [结果] 以三峡库区某滑坡为例，该滑坡在2种计算工况下的三维破坏概率分别为13.57%和21.77%，属低危险性，与滑坡实际情况基本一致，而滑坡二维破坏计算结果属中等危险性。 [结论] Rosenblueth方法计算的滑坡三维破坏概率能较好地评价滑坡的稳定性，其评价结果比二维破坏概率评价结果更为可靠。

关键词：有限元强度折减法; Rosenblueth方法; 三维破坏概率

破坏概率是滑坡稳定性定量评价的主要方法之一，目前关于滑坡破坏概率计算的研究成果较多[1-9]。已有的研究虽然取得了很多成果，但是主要集中在滑坡二维计算方面，从三维角度计算滑坡的破坏概率的研究还很少。为此，本研究运用FLAC 3D数值模拟软件，采取Rosenblueth方法计算滑坡的三维破坏概率，并将计算结果与二维破坏概率进行对比研究，以三峡库区某滑坡为例对三维破坏概率计算结果进行验证。

1Rosenblueth方法简介

对于一般的滑坡稳定性问题，建立状态函数：

Z=g(x1,x2,…,xn)

(1)

式中：x1，x2，…，xn——凝聚力、摩擦系数、孔隙水压力、容重等随机变量，它们大部分都服从正态分布或者对数分布。

Rosenblueth方法常用稳定性系数方程作为状态函数，即：Z=F(x1,x2,…,xn)-1=0。

在随机变量xi(i=1，2，…n)的分布类型未知的情况下，不用考虑它们的变化形态，只在区间(xmin，xmax)上分别对称地选取两个取值点，例如，一般取均值μxi的正负标准差，即

(2)

对于这n个随机变量，就会有2n个取值点，取值点的所有可能的组合有2n个。在这2n个组合情况下，根据极限状态函数计算公式，可以求得2n个极限状态函数Z，即有2n个稳定性系数。

如果n个随机变量相互独立，每个组合出现的概率相同，则Z的均值估计表达式为：

(3)

如果n个随机变量相关，并且每个组合出现的概率不同，则它们的概率值Pj的大小取决于随机变量间的相关系数ρ，即

(4)

式中：ei(i=1，2，…，n)取值为：当xi取xi1时，ei=1；当xi取xi2时，ei=-1，ρ(i-1)i表示随机变量xi-1与xi之间的相关系数。因此，Z的均值估计表达式为：

(5)

根据一阶原点矩和二阶中心矩的估计，可以通过推导得到极限状态函数概率分布的均值与方差。

(1) 一阶原点矩M1。随机变量Z的一阶原点矩，也称为均值μz，其点估计为

(6)

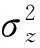
(7)

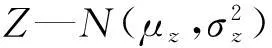
β=(μz-1)/σz

(8)

则滑坡的破坏概率为：Pf=1-φ(β)

(9)

2滑坡实例分析

2.1　滑坡简介

2.1.1滑坡概述该滑坡位于重庆市万州江南新区陈家坝办事处界内，位于长江右岸，滑体区内有一条镇级公路及一条村级公路东西向贯通整个滑体，交通较方便。

2.1.2滑坡的空间形态及物质组成

(1) 滑坡空间形态。滑坡体前缘临江，左右均以冲沟为界，后缘基岩出露，剪出口位于长江岸边。滑坡体平面呈箕形，剖面呈凸形。滑坡体高程分布130~325 m，长1 000 m，宽1 250 m，厚5～35 m，坡度5°~15°，主滑方向354°，总面积1.25×106m2，总体积2.50×107m3。

(2) 滑坡的物质组成及结构特征。滑坡体由第四系崩积、坡积成因的黄褐色粉质黏土夹砂岩碎块石、泥岩角砾组成，结构松散，土体可塑—硬塑状，砂岩碎块石、泥岩角砾含量约5%～60%。滑带主要为灰白色、黄褐色粉质黏土(黏土)夹砂岩碎石、泥岩角砾，可塑，细腻具滑感，吸水后泥化，黏性强。滑床主要为侏罗系中统沙溪庙组(J2s)泥岩、粉砂岩及砂岩组成，地层产状153°∠4°。泥岩为紫红色，泥质结构；粉砂岩为浅黄色，粉粒结构，主要成分为石英、长石，泥质胶结；砂岩为灰白色，中—细粒结构，主要成分为石英、长石，钙质胶结，具斜层理。

(3) 滑坡的水文地质条件。 ① 地表水特征：滑体右侧边界为一小溪，溪水向下直接流入长江，水量随季节变化。滑坡体上分布大量水塘，少量水塘积水可常年不干。 ② 地下水特征：滑坡区地下水为基岩风化裂隙水和第四系松散层孔隙水，主要由大气降水、灌溉水、生活污水的垂向补给和后缘地下水的侧向补给，向长江排泄或以湿地形式在前缘或低洼处出露。基岩风化裂隙水主要赋存于泥岩和砂岩风化带中，第四系松散孔隙水主要赋存于滑坡堆积的含碎块石粉质黏土中，富水性总体上较差。

2.2　滑坡三维破坏概率计算

2.2.1滑坡三维地质模型建立根据该滑坡的物质组成及结构特征可知，将滑坡的物理介质概化为滑体、滑带与滑床基岩三种介质，采用大型通用有限元软件ANSYS 10.0的前处理模块建模，滑坡地表通过点、线、面的生成顺序，建立滑坡的三维地质模型(图1)，并采用四面体单元进行网格剖分。模型共37 806个节点，194 758个单元。

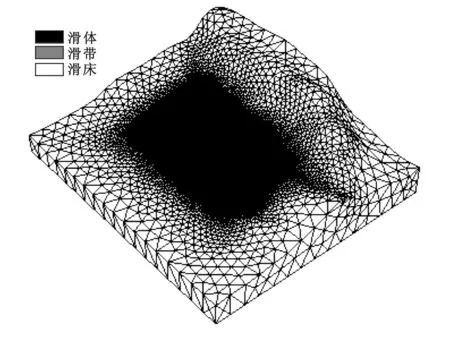
图1　滑坡三维地质模型

2.2.2计算工况选取根据三峡库区运行经验及国内外学者的研究成果，同时参照三峡库区地质灾害防治工作指挥部负责编制的《三峡库区三期地质灾害防治工程地质勘查技术要求(2004年)》，同时根据滑坡的实际变形情况，选取滑坡可能危险工况为滑坡的计算工况，即：工况①：自重+坝前水位从175 m降至145 m；工况②：自重+坝前水位从162 m降至145 m+汛期50年一遇暴雨。

2.2.3滑坡地下水渗流场模拟对于滑坡二维地下水渗流场模拟，采用Geostudio数值模拟软件中的seep/w模块对滑坡计算剖面进行模拟，而对于滑坡三维地下水渗流场模拟，这里采用多个滑坡纵剖面先进行二维模拟，然后将模拟出的多个剖面二维水位线连成面，即得到滑坡近似的三维地下水位面。

2.2.4抗剪强度参数选取根据该滑坡滑体地质勘查报告可知，滑坡滑带土的抗剪强度参数详见表1。根据文献[10]中提供的滑坡抗剪强度取值方法，得到该滑坡的抗剪强度参数概率分布函数详见表2。

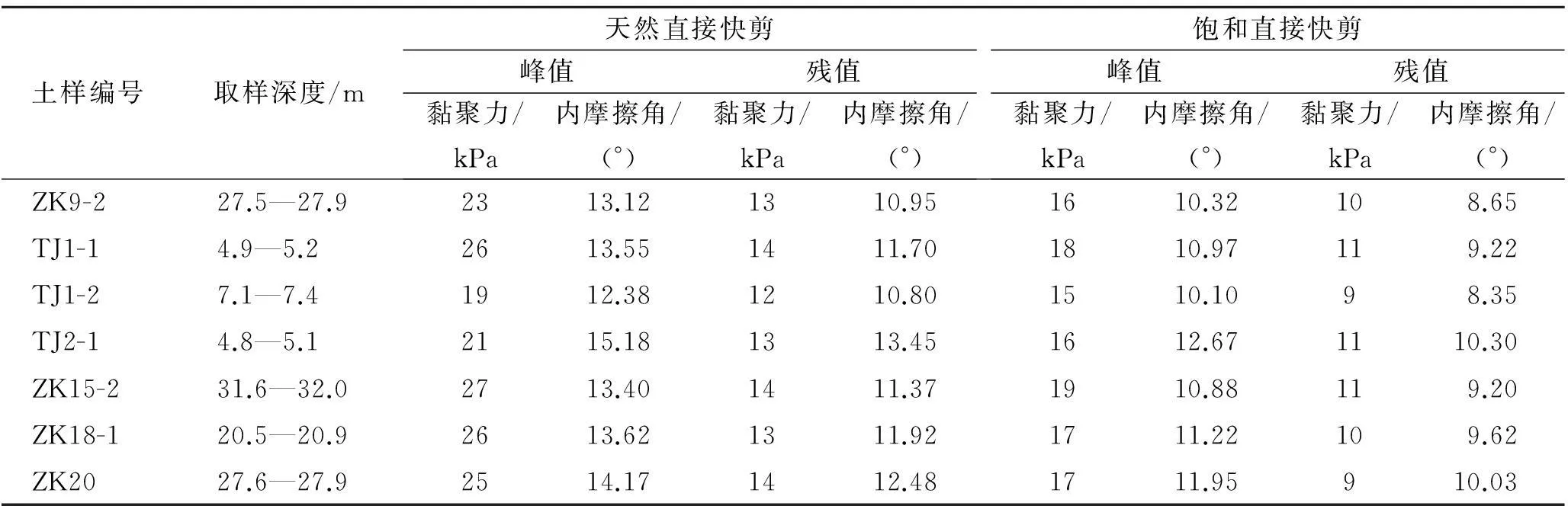
表1　滑坡滑带土抗剪强度参数室内试验值

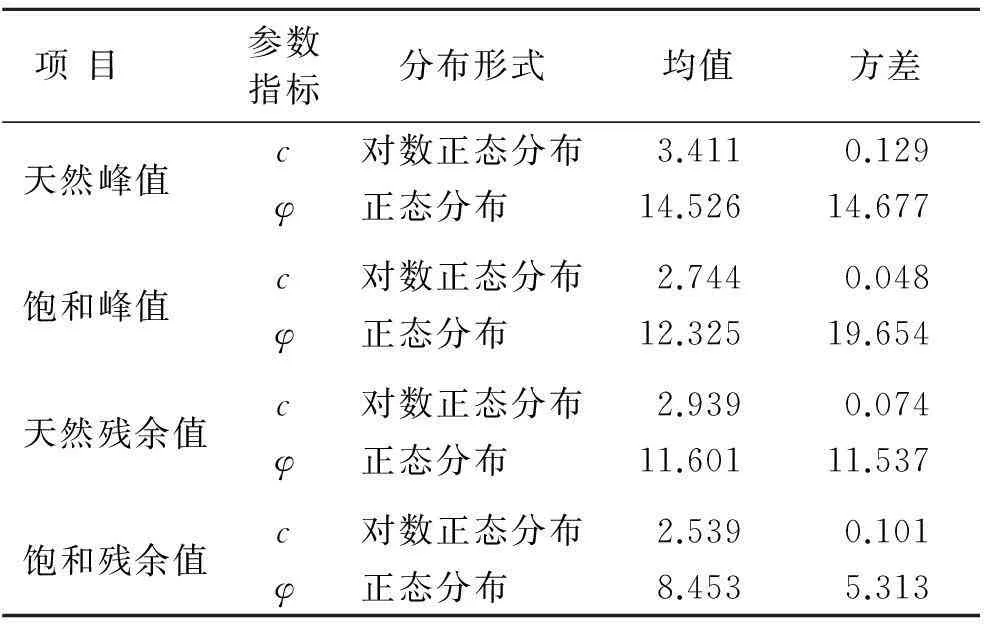
表2　滑坡滑带土抗剪强度参数概率分布函数

2.2.5滑坡破坏概率计算根据表2中的抗剪强度参数，采用前述Rosenblueth方法，运用FLAC 3D数值模拟软件计算滑坡的三维破坏概率，具体计算过程为：

(1) 工况①条件下：自重+坝前水位从175 m降至145 m。

令滑坡的状态函数Z=F(c、φ)，由于考虑的随机变量只有c，φ，故可以得到4个稳定性系数函数值分别为：

Z1=F(μc+σc,μφ+σφ)=1.60

Z2=F(μc+σc,μφ-σφ)=1.11

Z3=F(μc-σc,μφ+σφ)=1.46

Z4=F(μc-σc,μφ-σφ)=0.97

设随机变量c和φ相互独立，即ρc,φ=0，由公式(3)可得Pj=1/4

由公式(5)可得：

由公式(6)得：

=0.064 79

σz=0.255

从而得到该工况条件下滑坡的三维破坏概率为：

Pf=1-φ(β)=1-φ(1.10)

=1-0.8643=13.57%

(2) 工况②条件下：自重+坝前水位从162m降至145m+暴雨。

Z1=F(μc+σc,μφ+σφ)=1.48

Z2=F(μc+σc,μφ-σφ)=1.02

Z3=F(μc-σc,μφ+σφ)=1.33

Z4=F(μc-σc,μφ-σφ)=0.896

根据前述运算过程得到该滑坡在工况②条件下的破坏概率为：

Pf=1-φ(β)=1-φ(0.78)

=1-0.7823=21.77%

根据相关研究成果[9]可知，Rosenblueth方法和Monte—Carlo方法计算结果基本无差别，因此采用Geostudio软件中slope/w模块的Monte—Carlo方法计算滑坡的二维破坏概率，具体结果详见表3。

表3　滑坡破坏概率计算结果

结合表4中滑坡稳定程度分级标准，从表3可以看出，对于工况①和工况②，根据滑坡三维破坏概率的计算结果，滑坡整体为低危险性，而根据滑坡二维破坏概率计算结果，滑坡整体为中等危险性。

表4　滑坡稳定程度分级[11]

2.2.6滑坡稳定性计算结果验证根据重庆市万州环境监站提供的监测数据，绘制了滑坡12个位移监测点的水平方向累积位移—时间曲线(监测点WZ13-06位移太大未在图中描绘)，监测时间为2007年3月至2009年11月，监测周期为1个月1次，具体如图2所示。从图2可以看出，对于滑坡监测剖面Ⅰ-Ⅰ′，Ⅱ-Ⅱ′，Ⅲ-Ⅲ′，滑坡前缘监测点WZ13-03，WZ13-06，WZ13-09的位移都较大，滑坡中部监测点WZ13-02，WZ13-05，WZ13-08的位移相对较小，滑坡后部监测点WZ13-01，WZ13-04，WZ13-07基本变形很小，基本处于稳定状态；而对于滑坡监测剖面Ⅳ-Ⅳ′，WZ13-11，WZ13-12变形很小，且一直处于平稳状态。

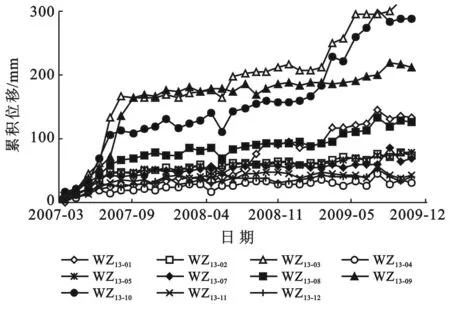
图2　滑坡地表水平方向累积位移-时间曲线

根据滑坡监测分析结果可知，滑坡整体目前较稳定，主要是滑坡前缘局部发生变形，滑坡整体失稳的可能性较小，滑坡整体处于低危险性，所以滑坡三维破坏概率计算结果更可靠。

3结 论

(1) 在计算工况①和计算工况②条件下，滑坡三维破坏概率分别为13.57%和21.77%。

(2) 在计算工况①和计算工况②条件下，滑坡二维破坏概率分别为41.08%和50.93%。

(3) 对于工况①和工况②，滑坡三维破坏概率的计算结果为低危险性，而滑坡二维破坏概率计算结果为中等危险性。

(4) 根据现场调查及专业监测滑坡整体应处于低危险性，所以滑坡三维破坏概率计算结果比二维破坏概率计算结果更可靠。

[参考文献]

[1]马淑芝,贾洪彪,唐辉明,等.稳定性可靠度分析在三峡库区二里半滑坡中的应用[J].地质科技情报,2005,24(S):177-179.

[2]苏永华,赵明华,李青海,等.稳定性系数为隐式函数的边坡可靠度近似计算方法[J].岩土工程学报,2006,28(10):1198-1203.

[3]徐江,杨更社,刘慧.基于蒙特卡洛模拟法的冻土边坡可靠度评价[J].地下空间与工程学报,2007,3(8):1433-1437.

[4]尹小涛,王水林.基于可靠度理论的滑坡稳定性及其影响因素分析[J].岩土力学,2008,29(6):1551-1556.

[5]吴振君,王水林,汤华,等.一种新的边坡稳定性因素敏感性分析方法:可靠度分析方法[J].岩石力学与工程学报,2010,29(10):2050-2055.

[6]彭振斌,李俊,彭文祥.基于Bishop条分法的边坡可靠度应用研究[J].中南大学学报：自然科学版,2010,41(2):668-672.

[7]张璐璐,邓汉忠,张利民.考虑渗流参数相关性的边坡可靠度研究[J].2010,27(1):114-119.

[8]张亚国,张波,李萍,等.基于点估计法的黄土边坡可靠度研究[J].工程地质学报,2011,19(4):615-619.

[9]黄丽娟,刘超,李萍,等.吉县水洞沟滑坡稳定性的可靠度分析[J].工程地质学报,2012,20(S1):544-549.

[10]汤罗圣,殷坤龙,李德营.基于推广Bayes方法参数优化的滑坡稳定性评价[J].地质灾害与环境保护,2010,21(4):33-37.

Failure Probability Calculation of Three-dimensional Landslide TANG Luosheng, YAN Tingzhou, DENG Changqing, YUE Min

(CommunicationsPlanning&DesignInstituteofHubeiProvince,Wuhan,Hubei430074，China)

Abstract：[Objective] Landslide occurrence probability was calculated and verificated using three-dimensional model to provide a new way for quantitative evaluation of landslide stability. [Methods] Rosenblueth method was used to calculate the probability of three-dimensional landslide by FLAC 3D numerical simulation software. Its result was compared with the one calculated by two-dimensional probability model. [Results] Taking a slope in the three gorges reservoir area as an example, we calculated the landslide probability under two kinds of working condition using two and three dimensional models. According to the result form the three dimensional model, the probability were 13.57% and 21.77%, respectively, both belonging to low risk level. These probabilities were thought to be the actual situation. However, the calculated probabilities from two-dimensional model were as high as medium risk level. [Conclusion] Rosenblueth method performed more reliable than two-dimensional probability evaluation models do in evaluating landslide stability.

Keywords:finite element shear strength reduction method; Rosenblueth method; three-dimensional failure probability

文献标识码：B

文章编号：1000-288X(2015)06-0164-04

中图分类号：X43

收稿日期：2014-09-09修回日期：2014-10-12

第一作者：汤罗圣(1984—),男(汉族),湖北省石首市人,博士,工程师，主要从事地质灾害机理及预测预报研究。E-mail:homeandm@163.com。