《线性代数》课程新型教学模式探讨
2015-03-15张映辉
陶 霞, 张映辉
(湖南理工学院 数学学院, 湖南 岳阳 414006)
《线性代数》课程新型教学模式探讨
陶 霞, 张映辉
(湖南理工学院 数学学院, 湖南 岳阳 414006)
主要讨论新型教学模式, 使得师生在《线性代数》课程教学效果上达到双赢. 面对《线性代数》课程教学内容多、课时安排偏少的特点, 提出精简教学内容、运用多媒体和数学软件辅助教学以及结合实际问题研究线性代数的一些应用.
线性代数; 新型教学模式; 教学改革
在传统的教学模式上, 教师以“一支粉笔, 一块黑板”演绎着单调的教学人生. 这种“满堂灌”的教学模式严重缺乏师生之间的交流, 学生的主观能动性远未被调动起来, 从而忽视了学生自主创新能力的培养,远达不到预期的教学效果. 在二十一世纪信息化时代背景下, 这些90后的大学生们从小就接触到电脑和网络, 能够及时了解各种最新信息, 拓宽了视野, 接受新事物的能力强. 针对这些特点, 我们急需寻求适合大学生全面发展的新型教学模式, 激发大学生们的学习热情. 在教学效果上, 不仅能提高教学质量, 而且有利于学生发散性思维和创造性思维的形成.
《线性代数》课程是理、工、经、管等专业必修科目, 是不可缺少的专业基础课程. 科学计算领域中,只存在极少数的线性问题, 能经过简单的数学知识得以解决. 在一些工程实际问题中, 大多数都表现为非线性的形式. 在一定的条件下, 某些非线性问题可转化为线性问题. “线性代数”课程所介绍的方法为解决线性问题提供了一套理论和计算工具, 能广泛应用于各学科中. 随着社会的进步和科技的飞速发展, 解大型线性方程组、求矩阵的特征值与特征向量等问题已经成为工程技术人员经常遇到的问题. 因而, 对于理工科各相关专业的学生来说, 他们必须具备线性代数的基本理论知识, 并熟练掌握其基本方法. 该课程具有学时少、内容抽象、逻辑性强、运算法则多等特点, 教师需站在一定的高度来统筹规划该课程的教学, 做到前后章节在内容上的融会贯通. 因此, 打破传统“满堂灌”的教学模式, 构建新型教学模式十分必要. 本文结合线性代数课程的特点和多年积累的课堂教学经验, 探讨一套新型教学模式在线性代数课程上的应用, 为线性代数的教学改革提供一定的参考.
《线性代数》课程新型教学模式的探讨主要从以下几点展开:
(1) 合理调整课程体系, 优化教学内容
《线性代数》课程内容主要有: 行列式的计算、矩阵的计算、矩阵初等变换、线性方程组, 以及线性相关性、相似矩阵及二次型、线性空间与线性变换等. 前部分内容偏重计算, 学生容易掌握; 后部分内容偏重理论, 学生难以理解. 而且教学任务要求在一个学期内完成, 课时安排偏少. 面对这些特点, 如何在教学过程中把握内容的广度和深度成为值得师生们共同思考的问题. 为了使学生能更好的掌握线性代数课程基本理论和计算方法, 并熟练运用这些知识有效解决一些实际问题, 探讨《线性代数》课程新型教学模式显得尤为重要, 具有理论和实际意义. 且可以为学生进一步学习后续课程奠定重要的数学基础.
例如在讲解“克拉默法则”这部分内容时, 可从求解二元一次方程组出发, 通过消元法得到方程组的解, 启发学生其解可用行列式的形式来表达. 紧接着, 举一个五元一次方程组, 启发学生从行列式这个角度进行求解, 熟悉用克拉默法则来求解多元一次线性方程组过程. 然后举几个系数行列式为零的具有代表性的特例, 比如三元一次方程组中其中一个方程能由另外两个方程表示出来, 启发学生发现克拉默法则所适应的条件. 从另一个角度看, 矩阵的概念及运算、线性变换、线性相关性、线性空间等概念凸显出来, 通过这些特例来理解抽象的理论知识, 将整个教学内容用“解线性方程组”这条线串起来, 在这种新型教学模式下, 学生的求知欲被逐步激发起来, 增强了学习的兴趣. 最后, 和学生一起总结克拉默法则, 加深对这部分内容的理解. 另一方面, 合理地将线性代数与高等数学、解析几何等课程的内容整合起来, 让学生从不同的角度来理解《线性代数》课程, 使学生感受到这些数学问题可以融会贯通, 对将来的工作也非常重要. 这种新型教学模式不仅培养学生自主发现问题、有效解决问题的能力, 而且能培养学生以发散思维来多角度考虑问题, 从而达到培养创新能力的目的.
(2) 改革教学手段, 丰富教学内容, 采用多样化的教学方法, 凸显理论与应用相结合
线性代数课程的特点是理论性、概念性比较强, 涉及到大量的数学理论推导, 若不注意教学方法, 则很容易会让学生觉得枯燥. 在教学过程中, 通过介绍基本概念和计算方法, 结合多媒体课件和一些实际问题进行课堂演示, 突出行列式、矩阵、线性变换等数学概念, 注重理论联系实际, 突出实际应用, 从实例分析中强化理论概念, 加深学生对该课程的认识和理解, 从而牢固掌握其中的基本概念、基本分析方法和运算方法.
传统上, 教师一般采用单一的黑板教学模式, 大部分课堂时间用在计算推导上, 而关于理论和相关的应用的讲解基本没有安排到课堂中来, 造成整个课堂内容重难点不突出, 不利于学生抓住课堂的脉络所在, 更不利于学生抽象思维的形成, 难以达到预期的教学目标.
随着信息化高速发展, 学生能从网络上了解到更加丰富的学习资源, 拓宽了视野, 接受新事物的能力增强. 而运用多媒体进行辅助教学, 能使得课堂讲解更直观、更具吸引力, 能将新旧知识串联起来, 加深学生对新知识点的认识和理解程度, 有效解决和协调线性代数课程内容过多和学时安排过少之间的矛盾.因此, 采用黑板加多媒体的教学模式, 既能保留传统教学法的特点, 也能增加课堂教学容量, 提高教学效率. 为了了解线性代数课程在各领域中发展的最新动态, 扩大学生学习该课程的知识背景, 提高学生应用能力和创新能力的培养, 可充分利用网络资源和相关数学软件(如MATLAB和MATHEMATICA等)辅助进行课堂演示. 这样, 不仅提供了丰富的学习资料, 而且调动了学生的积极性, 能达到良好的教学效果.
“逆矩阵”是线性代数课程的一个重要知识点. 下面尝试用新型探究式教学模式来具体分析这一教学内容.
首先引出逆矩阵这一概念. 在数的乘法中, 如果a是非零常数, 则存在a的逆, 使. 这使得求解一元线性方程ax=b变得非常简单, 即在方程两端左边乘以a-1, 可得1·x=x=a-1b.在矩阵的乘法中, 单位矩阵I起着数1在数量的乘法中的类似作用. 因此问: 对于n阶方阵A, 是否也存在着“逆”, 即是否存在一个n阶方阵B, 使得AB=BA=I?从而引出“逆矩阵”这一概念, 给出其定义. 并通过精心制作的课件展示逆矩阵在实际生活中的一些应用, 例如逆矩阵在密码问题中的应用.
通过信息编码学的知识, 我们可利用可逆矩阵来破解矩阵密码. 比如可将数字和26个英文字母建立一一对应的关系:
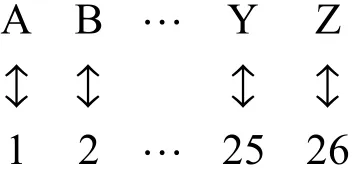
如果要发信号“SEND MONEY”, 通过建立与数字的一一对应关系, 这条信号的编码变成19, 5, 14, 4, 13, 15, 14, 5, 25, 这里5表示字母E. 然而这样的编码非常容易遭到破解. 因此, 我们希望寻求更为可靠的编码方法. 如果对一个信号进行较长的编码, 我们往往会根据某些数字频率出现的高低来判断. 频率最高的数字可能代表某个字母, 比如上面出现频率最高的数字5就代表字母E.
为得到更有效的编码, 我们可利用矩阵乘法来编码. 首先对信号“SEND MONEY”加密, 形成“密文”后传递出去. 这样增加未登录用户破解“密文”的难度, 也使得登录用户能轻轻松松解密. 对于一个元素都为整数的矩阵A, 而且其行列式|A|=±1, 那么由可知,A-1的元素均为整数. 通过矩阵A建立明文加密的方式, 加密后的“密文”就很难破解了. 取

为得到“密钥”矩阵A, 可对单位矩阵I进行有限次的矩阵初等变换, 比如采用将某行的整数倍加到另一行中等形式. 这样可得到元素都为整数的矩阵A. 而且由于|A|=±1可知,A-1的元素都为整数.
通过这个实例, 学生对逆矩阵有了初步的认识, 并带动学习逆矩阵的兴趣. 然后趁热打铁, 启发式的提出问题: 什么样的方阵有逆矩阵?如果存在逆矩阵, 如何去计算该逆矩阵?这样, 学生开始思考计算逆矩阵的一些方法. 下面给出方阵A可逆的充分必要条件为矩阵行列式|A|≠0, 而且, 其中A*为矩阵A的伴随矩阵. 根据此定理, 来计算密码应用中的A-1. 这样学生就能掌握计算逆矩阵的方法.
最后, 打开MATLAB软件, 先把A矩阵输入到命令窗口:
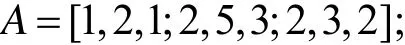
再输入求逆矩阵的命令:inv(A), 此时A-1矩阵就可以得到. 通过现场演示, 学生们能切身感受到数学软件是一种重要的计算工具, 不仅方便, 而且计算快, 结果准确. 同时也激发起学生们学习数学软件的兴趣,为以后解决实际工程问题打下扎实的基础.
采取这种新型的教学模式, 不仅教师能把逆矩阵这一重要知识点讲透彻了, 而且学生能够感受到逆矩阵在实际问题中的广泛应用, 并用数学软件计算逆矩阵. 这样, 教师和学生都是课堂上的“主角”, 教师起到抛砖引玉的作用, 学生进入主动学习的角色, 双方处于一种双赢的状态, 达到了理想的教学效果.
[1] 楼螂嬛, 马晓锐. 对线性代数探究式教学的探讨[J]. 价值工程, 2011, 30 (26)
[2] 陈凤娟. 线性代数的教学研究[J]. 高师理科学刊, 2012, 32 (1)
[3] 李小新, 桂旺生. 《线性代数》课程教学改革的实践与思考[J]. 池州学院学报, 2008, 2 (5)
[4] 阮万清, 张鸿艳, 顾 娟. 线性代数课程教学模式探讨[J]. 教学模式创新, 2013, 15
[5] 高淑萍, 孙 群, 杨 威, 等. 线性代数课程MATLAB实验内容的教学与研究[J]. 中国电子教育, 2007, 4
[6] 万正苏, 孙明保, 陶 霞. 浅谈线性代数中一些基本概念的教学[J]. 湖南理工学院学报(自然科学版), 2013, 26 (2)
Research on the New Teaching Model for the Course Linear Algebra
TAO Xia, ZHANG Ying-hui
(College of Mathematics, Hunan Institute of Science and Technology, Yueyang 414006, China)
This paper mainly discusses the new teaching model in order to get the win-win situation in the teaching effect of the course “linear algebra”. Actually the courseLinear Algebrahas the properties of large amount of content and small class time arranged, this paper proposes reducing the teaching content, using multimedia and mathematical software to assist teaching courses, and studying some applications of linear algebra combined with practical problems.
Linear Algebra; new teaching model; teaching reform
G642
A
1672-5298(2015)02-0088-03
2015-02-25
湖南理工学院教改项目(2013C06); 湖南理工学院教改项目(2013B09); 湖南省教育科学“十二五”规划课题(XJK015QGD007)
陶 霞(1982 − ), 女, 湖南湘阴人, 博士, 湖南理工学院数学学院讲师. 主要研究方向: 微分方程数值解
