一个单变量积分公式在重积分上的移植及其应用
2015-03-15张志红孙明保
张 婷, 张志红, 孙明保
(湖南理工学院 数学学院, 湖南 岳阳 414006)
一个单变量积分公式在重积分上的移植及其应用
张 婷, 张志红, 孙明保
(湖南理工学院 数学学院, 湖南 岳阳 414006)
将一个单变量积分公式移植到二、三重积分上, 然后再利用这些公式证明积分学中的一系列计算公式.
定积分; 曲线积分; 曲面积分; 重积分
引言
积分学中积分公式丰富多彩, 有些积分公式在积分学中起着支柱作用, 但这些公式的推导过程往往冗繁复杂, 不易理解和掌握, 如文[1~3]只证明了平面曲线的弧长公式以及第一型曲线积分的计算公式,而另外一些积分公式没有给出证明, 如第一型曲面积分的计算公式等. 本文将一个单变量积分公式移植到二、三重积分上, 然后再利用这些公式证明积分学中的一系列计算公式.
1 一个单变量积分公式及其在重积分上的移植
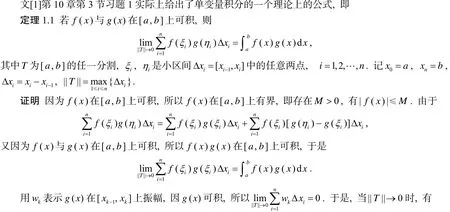

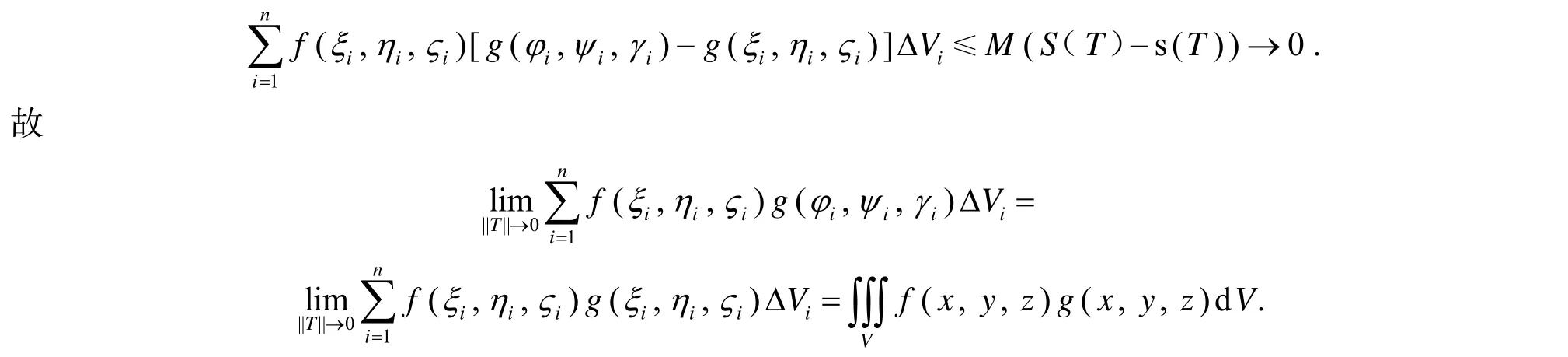
2 若干计算公式的证明
由以上三个定理可以方便地证明曲线弧长计算公式, 旋转体侧面积计算公式, 第一、二型曲线积分公式, 以及第一型曲面积分公式.




[1] 华东师范大学数学系. 数学分析(上、下册)[M]. 第4版. 北京: 高等教育出版社, 2010
[2] 宋国柱, 任福贤. 数学分析教程(下册)[M]. 南京: 南京大学出版社, 2013
[3] 刘玉琏. 数学分析讲义(上册)[M]. 第4版. 北京: 高等教育出版社, 2003
[4] 毛羽辉. 数学分析选论[M]. 第2版. 北京: 科学出版社, 2003
[5] 孔祥庆. 空间曲线的弧长一般求长法[J]. 南方冶金学院学报, 2001(4): 290~292
[6] 陆小庆, 颜 超, 孔 倩. 平面曲线弧长极坐标公式探讨[J]. 高师理科学刊, 2013(3): 9~11
[7] 倪 华, 田立新. 旋转曲面面积的曲线积分表示[J]. 高等数学研究, 2011(2): 33~34
[8] 李艳丽, 王 骋. 旋转曲面面积的计算方法[J]. 纺织高校基础科学学报, 2008(3): 27~30
[9] 费定晖, 周学圣. 吉米多维奇数学分析习题集题解[M]. 第4版. 山东: 山东科学技术出版社, 2012
[10] 裴礼文. 数学分析中的典型问题与方法[M]. 第2版. 北京: 高等教育出版社, 2006
The Transplantation of a Single Variable Integral Formula on Multiple Integral and Its Application
ZHANG Ting, ZHANG Zhi-hong, SUN Ming-bao
(College of Mathematics, Hunan Institute of Science and Technology, Yueyang 414006, China)
A single variable integral formula is transplanted into the double and triple integral and a series of integral formulas are proved by using these formulas.
definite integral; curvilinear integral; surface integral; multiple integral
O172.2
A
1672-5298(2015)02-0021-06
2015-05-07
张 婷(1993− ), 女, 湖南岳阳人, 湖南理工学院数学学院2011级本科生. 主要研究方向: 基础数学
