可压Navier-Stokes-Poisson方程组强解的整体存在性
2015-03-15张美花
张美花
(厦门华天涉外职业技术学院 基础部, 福建 厦门 361102)
可压Navier-Stokes-Poisson方程组强解的整体存在性
张美花
(厦门华天涉外职业技术学院 基础部, 福建 厦门 361102)
主要考察了可压NSP方程组强解的整体存在性. 由于初始数据属于不同的空间, NSP方程组强解的整体存在性也有所不同.
NSP方程组; 强解; 整体存在性
可压NSP方程组描述了半导体中带电荷粒子的运动传输. 一般地, 由于离子的质量比电子的大得多,在运动过程中惯性也要大得多, 为了简便处理, 我们将离子看作不动, 那么此时离子只提供了一个正的常电荷背景. 在这种情况下, 可压NSP方程组取单极的形式, 即只包含描述电子运动规律的方程. 但是将离子视为不动, 终究是一个理想的假设. 另一种情况就是离子和电子在电场力的作用下同时运动, 它们之间也会有相互作用. 这种情况就要比只考虑电子运动复杂得多, 但更符合现实, 称为双极情形. 近些年, 大量的数学工作者研究了单极或双极可压NSP方程组解的适定性, 其中在强解方面都取得了不少成果.
2010年, H. L. Li, A. Matsumura 和G. J. Zhang[7]研究了如下三维可压等熵Navier-Stokes-Poisson方程组的Cauchy问题:




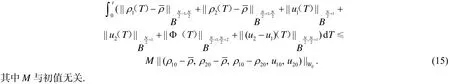
根据大量数学工作者研究了的单极或双极可压NSP方程组解的适定性, 本文主要考察了可压NSP方程组强解的整体存在性. 针对初始数据属于不同的空间, 全面总结了NSP方程组强解的整体存在性的不同,为我们继续研究NSP方程组提供了较为全面的参考资料, 有利于进一步研究和理解可压NSP方程组强解的其他性态.
[1] D. Hoff and K. Zumbrun.Pointwise decay estimates for multidimensional Navier-Stokes diffusion wave[J]. Z. Angew. Math. Phys., 1997(48): 597~614
[2] L. Hsiao, H. L. Li, T. Yang and C. Zou.Compressible non-isentropicbipolar Navier-Stokes-Poisson system inR3[J]. Acta Mathematica Scientia, 2011, 31B(6): 2169~2194
[3] D. L. Li.The Green’s function of the Navier-Stokes equations for gas dynamics inR3[J]. Comm. Math. Phys., 2005(257): 579~619
[4] H. L. Li, T. Yang and C. Zou.Time asymptotic behavior of the bipolar Navier-Stokes-Poisson system[J]. Acta Mathematica Scientia, 2009, 29B(6): 1721~1736
[5] H. L. Li and T. Zhang.Large time behavior of solutions to 3D compressible Navier-Stokes-Poisson system[J]. Science China Mathematics, 2012(55): 159~177
[6] Y. Q. Lin, C. C. Hao and H. L. Li.Global well-posedness of compressible bipolar Navier-Stokes-Poisson equations[J]. Acta Mathematica Sinica, 2012(28): 925~940
[7] A. Matsumura and T. Nishida.The initial value problem for the equation of motion of compressible viscous and heat-conductive fluids[J]. Proc. Japan Acad. Ser. A, 1979(55): 337~342
[8] C. X. Miao.Harmonic Analysis and Its Application in Partial Differential Equations[M]. Science Press, 2006
The Global Existence of the Compressible Navier-Stokes-Poisson Equations
ZHANG Mei-hua
(Department of Public Infrastructure, Xiamen Huatian International Vocation Institute, Xiamen 361102, China)
This paper investigates the NSP equations can be pressed in the global existence of strong solution. Because of the initial data belong to different space, the NSP equations of strong global existence of solution is also different.
Navier-Stokes-Poisson equations; strong solution; global existence
O175.2
A
1672-5298(2015)02-0013-05
2015-04-21
张美花(1977− ) , 女, 江西金溪人, 硕士, 厦门华天涉外职业技术学院基础部讲师. 主要研究方向: 应用数学
