考虑水化度对热学参数影响的早期混凝土温度场分析

崔 溦 吴甲一 宋慧芳

(天津大学水利工程仿真与安全国家重点实验室，天津300072)

混凝土浇筑后受自身水化反应影响，温度会在短时间内急剧增大，体积膨胀变形[1].此时，混凝土处于(超)早期阶段，受弹模变化及温度变化影响，混凝土将会产生较大的残余应力，而该阶段混凝土的抗拉强度较低，易导致温度裂缝的产生，从而对结构安全性产生重要影响.

数值计算方法由于其独特的优越性，已成为研究结构问题的重要手段，材料参数取值的合理与否关系到数值模拟结果的准确性.现阶段，早期混凝土的温度应力研究基本都采用温度场和应力场顺序耦合的方法.因此，准确地求解温度场就成为计算应力场的基础.早期混凝土性态与水化过程密切相关:随着水化放热，混凝土由流态过渡到塑性，进而成熟固化，与此相关的热力学参数，如导热系数和比热容，也必然发生变化.国外研究学者通过大量的试验研究了参数的变化规律及其影响因素[2-3]，研究结果表明早期混凝土的导热系数相对于固化后混凝土的导热系数偏高.而现有的温度场计算方法基本上没有考虑早期混凝土导热系数和比热容随水化过程的变化[4-5]，不能真实地反映早期的温度变化过程，导致温度场与实际情况之间产生较大误差.

本文基于ABAQUS二次开发平台，考虑早期混凝土热学参数随水化度的变化规律，开发了用于温度场计算的UMATHT和FILM子程序.其中，UMATHT子程序用来模拟混凝土水化热过程，实现早期温度场参数随水化度的变化;FILM用来模拟混凝土表面与空气接触的第3类边界条件.在验证了子程序合理性的基础上，通过对试验结果的模拟对比，分析了早期混凝土温度场模拟考虑热学参数变化的重要性.

1 试验

1.1 原材料

试验所用水泥为唐山奥成牌PO42.5R快硬硅酸盐水泥，比重为3.1，细度为350 m2/kg，颗粒平均粒径为19.1 μm;细骨料为海砂，Ⅱ区级配，细度模数2.3，密度2.56 g/cm3;粗骨料为石灰岩碎石颗粒，比重为2.57，最大颗粒粒径20 mm，连续级配.

1.2 温度传感器

温度传感器主要用于测量试件温度变化，本文采用的温度传感器为长沙金码高科技实业有限公司生产的JMT-36C智能温度传感器，其精度为0.1℃，量程为－20～120℃.此外，温度传感器与数据采集仪和电脑相串联，可按设定的时间间隔采集温度数据.

1.3 试验方案

为达到理想的试验效果，试件的形状必须满足以下要求:方便在实验室内操作且易于数值模拟;试件必须能够产生足够的温度梯度用于监测.按照以上要求，试件的尺寸拟定为600 mm×300 mm×600 mm(见图1)，其体积为 0.108 m3.试件外表面包裹一层用以保温的25 mm厚聚苯泡沫板和起固定作用的10 mm厚胶合板.

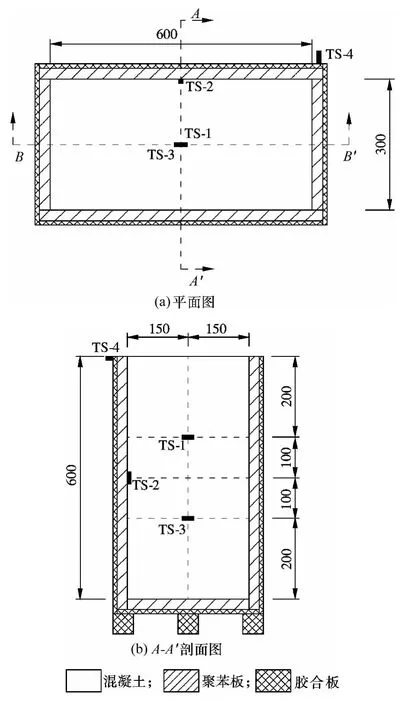
图1 试件尺寸及传感器位置图(单位:mm)

在混凝土浇筑前，先在浇筑模具内表面接缝处涂抹约2 mm厚的硅胶，然后将聚苯泡沫板贴在模具内表面，聚苯板接缝处密封，后期浇筑完成后，试件顶部同样用聚苯板密封，起到保温和防止水分蒸发的作用.然后，将2个振弦传感器和3个温度传感器固定在模具内部，将1个温度传感器布置在模具外表面，具体布置位置详见图1和图2.其中TS-1和TS-3用以验证试件内部的温度变化，TS-2用以验证数值模型的温度边界条件，TS-4用以测量环境温度的变化.此外，在TS-1和TS-3处布置了振弦传感器用来测量应变，本文中不涉及应变的模拟，故下文中忽略应变测量值.

图2 试验装置及传感器概图

完成上述准备工作后，浇筑混凝土试件，混凝土试件配合比如表1所示.首先，将混凝土充分搅拌后通过大漏斗浇筑到模具内部，避免直接浇筑对传感器造成冲击从而导致其位置偏移，同时，使用小型振捣棒振捣混凝土.浇筑完成后立即采集数据，每隔0.5 s采集一次.

表1 混凝土配合比 kg/m3

1.4 试验结果分析

利用温度传感器测量的混凝土试件温度如图3所示.由图可知，受水泥水化反应影响，混凝土温度经历了一个先增加后减小的变化过程.TS-1与TS-3温度变化基本一致，尤其是前20 h，后期TS-1温度逐渐低于TS-3;TS-2前期温度变化规律与TS-1和TS-3基本一致，但数值上有一定差别.TS-4测得的室内环境温度变化较小，基本处于23℃(±0.5℃)，其中测得的混凝土温度峰值TS-1为60.95 ℃(6 h);TS-2为58.75 ℃(6.5 h);TS-3 为61.75 ℃(5.5 h).从图中可以看出，TS-3 测点的温度增长较快并且温升最高，出现这种现象主要是因为TS-3布置于混凝土试件中部，其环境相对更接近于绝热状态;而TS-1测得的温度变化规律与TS-3大致相同，后期温度降低速度略大于TS-3的温度降低速度，降低速度的不同是因为TS-1相较于TS-3更接近顶部，散热效果更好.从图中同样可看出，混凝土刚浇筑完成就开始了水化温升阶段，一直持续到6 h;其后开始降温阶段，鉴于试验是用以验证适用于早期混凝土温度场的变化规律，因此数据仅记录到188 h.

图3 温度传感器测量值

2 数值模拟参数

水泥水化热是影响混凝土温度场的重要因素，但传统方法在模拟过程中仅考虑了龄期对水化热的影响而忽略了温度的影响[4]，即假设各单元在相同的时间段内释放的热量是相同的，这与结构内部水化快、升温高、放热快的事实不符.同时，在参数选择方面传统方法也有待商榷.因此，本文计算时采用考虑水化度影响的温度场计算模型，并考虑热学参数随水化度的变化过程，以实现对早期混凝土温度场更加准确的模拟.

2.1 等效龄期成熟度

成熟度的核心思想是同种混凝土的不同部位不论它们的温度和时间怎么组合，只要两者具有相同的成熟度值，则它们的强度完全相同[5].

基于混凝土温度历程计算成熟度的方程[6]如下:

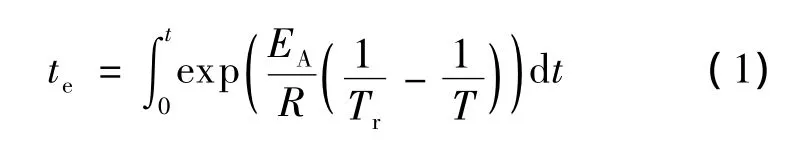
式中，te为混凝土的等效龄期;EA为反应活化能，J/mol;R为理想气体常数，8.314 J/(mol·K);Tr为参考温度(通常取20℃，即293 K);T为节点的实际绝对温度.对于混凝土材料，当绝对温度T≥293 K时，EA=335 kJ/mol;当T＜293 K时，EA=(335+147 × (293 － T))kJ/mol[7].本文在计算时选用EA/R为恒定值2 700 K.

2.2 水化度

水化度概念是基于Arrhenius反应速率公式和材料活化能提出的，被定义为水化反应中已经消耗的水泥量相对于水泥总量的比值，其值介于0(开始时刻)和1之间.混凝土水化度受混凝土材料组成、水灰比等的影响.对同种混凝土不同部位，不论其时间和温度如何组合，只要具有相同的水化度值，其物理性能也相同，这与成熟度的本质相吻合.基于上述思想，国外研究学者将等效时间和水化度联系起来，根据试验提出了一些关系式，常用的主要包括复合指数型、双曲线型以及指数型，其表达式分别如下[8]:

式中，α(te)为基于等效龄期的水化度;m，n，λ1，C，a，b为常数，可根据试验结果拟合，也可通过类似工程取值.

从以上关系模型可看出，早期混凝土等效龄期成熟度和水化度存在一定的对应关系.通过水化度将混凝土等效龄期成熟度与混凝土热力学性态联系起来，可以更加准确地表达混凝土温度、时间对材料热力学特性的影响.

2.3 早期混凝土热学参数

混凝土的热学性能参数主要包括导温系数a(m2/h)、导热系数k(kJ/(m·h·℃))、比热容c(kJ/(kg·℃))和密度ρ(kg/m3).混凝土的热学性能与骨料、容重及含水状态有关[9].不同混凝土由于材料、配合比等不同导致参数有一定差别，对混凝土温度场分布也有不同程度的影响.根据导温系数的定义，有

混凝土的热学性能一般由针对性的试验测定，且只需测定4个参数中的3个，另一个可由式(6)计算得到.

1)导温系数是反映混凝土热量扩散的一项综合指标，亦称热扩散系数.导温系数愈大，愈有利于热量的扩散，其表达式见式(6)，混凝土的导温系数取值一般介于0.003～0.005 m2/h之间.

2)在早期混凝土温度场求解过程中，导热系数的正确选择关系到温度场模拟的精确程度.影响混凝土导热系数的因素主要是配合比、骨料类型以及混凝土含水状态[10].国外研究学者通过试验研究表明，硬化过程中的混凝土其导热系数要比硬化后的值大21% ～30%，试验表明内部混凝土的导热系数要大于表面部位的导热系数[11].早期混凝土导热系数的变化过程可通过线性公式表达[12].Schindler[13]建立了早期混凝土导热系数与混凝土水化度之间的关系:

式中，k(α)为导热系数;ku为混凝土硬化后最终的导热系数;α为水化度值.

3)比热容是表示物质热性质的物理量.试验研究表明，温度和水分对混凝土比热容的影响很大，硬化过程中比热容与水化度成线性反比变化规律.Van Breugel[14]通过研究给出了早期混凝土比热容的变化公式:

式中，Wc，Wa，Ww分别为每立方米混凝土中水泥、骨料和水的质量，kg;cc，ca，cw分别为水泥、骨料和水的比热容值;ccef为混凝土水泥的假定比热容值;Tc为当前温度，℃.

4)混凝土密度是指单位体积混凝土的质量，它随骨料的密度、级配混凝土的配合比以及干湿程度等因素变化而变化.

3 基于水化度的温度场二次开发

3.1 基于水化度的热传导方程

早期混凝土水化反应与自身的温度、龄期有关，其热学参数也随水化反应程度而不断变化，因此早期混凝土水化反应热传导方程是一个较为复杂的非线性问题.基于水化度建立的热传导方程为

式中，c(te)为比热容;k为基于水化度的导热系数，可由式(7)计算得出;θ为基于水化度的绝热温升;τ为龄期.

在有限元计算中，采用时间步累计叠加的形式计算相应的等效龄期值，即

3.2 温度场开发

对于早期混凝土温度场的模拟需要使用UMATHT和 FILM两个用户子程序.其中，UMATHT子程序用来模拟混凝土的水化放热过程，FILM子程序用来模拟混凝土与空气接触的第3类边界条件(包括表面拆模或温度骤降等过程).

UAMTHT子程序编写的核心语句就是定义增量步结束时的混凝土单位质量的内能U和热流矢量FLUX.用户可通过函数式来定义变化的比热容和导热系数，通过温升方程模拟混凝土绝热温升过程，用户也可通过等效的方法来模拟冷却水管的作用.

FILM子程序编写的核心语句就是定义混凝土表面与外界的热交换系数H(1)，以及定义大气温度随时间的变化过程的方程SINK.用户可通过判断SNAME的名称对不同的外表面定义不同的随时间变化的热交换系数，例如模拟混凝土结构拆模或因其他原因引起结构的外表面热交换系数的变化时，可通过判断不同的SNAME名称来定义热交换系数的变化.用户也可通过定义SINK模拟寒潮引起的温度骤降等气候条件.

4 数值模拟分析

4.1 有限元计算

对1.3节中描述的试件采用3D有限元的方法进行数值模拟，如图4所示.计算时间为自浇筑完成后的188 h(假设一次浇筑完成)，混凝土材料参数见表2.

图4 有限元模型

对本次试验，混凝土绝热温升方程如下所示[15]:

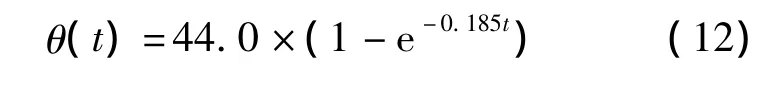
在温度场模拟过程中，由于混凝土试件顶部、底部及侧面具有保温板及模板，因此这些部位可按照第3类边界条件来计算.等效表面散热系数βs计算公式如下[1]:

式中，β为保温板在空气中的散热系数;hi为保温板厚度;λi为保温板的导热系数.

根据式(13)，试件顶部热交换系数取为28.8 kJ/(m2·h·℃)，其他边界热交换系数取为15.12 kJ/(m2·h·℃)，顶部热交换系数取值较高的原因是试验中顶部密封仅使用了聚苯板，而四周与底部除聚苯板外还有胶合板，故计算得出的顶部热交换系数较大.

按以下2种工况分别计算模拟试验中温度的变化过程.

工况1 混凝土绝热温升采用传统的指数型公式，见式(7).混凝土导热系数及比热容取值见表2，其中导热系数和比热容在计算过程中均不发生变化.

工况2 引入等效龄期概念，采用基于水化度的温度场模型，同时考虑变化的比热容和导热系数.导热系数由式(7)计算确定，其中水化度公式为α(te)=1－exp(－0.185te)，ku见表2.比热容由混凝土配合比、式(10)和式(11)共同计算确定，其中参数取值分别为Wc=400 kg，Wa=1 565 kg，Ww=200 kg;cc=1.14 kJ/(kg·℃)，ca=0.678 kJ/(kg·℃)，cw=4.187 kJ/(kg·℃).从图3 可看出，试件所处的室内环境温度围绕23℃上下波动，其波动幅值不超过0.5℃，因此计算过程中外界温度取为定值23℃.

4.2 温度场结果及分析

为了验证数值模拟的准确性，将数值模拟试件上监测点处的温度变化与试验结果对比，如图5所示.

图5 各测点数值模拟结果与试验结果对比

图5给出了TS-1，TS-2及TS-3三个监测点的不同工况下温度对比曲线.从图中可看出，工况1和工况2的温度变化规律与实测温度变化规律基本一致，但是两者的温度峰值及达到温度峰值的时间有较大差别.其中 TS-1实测的温度峰值为60.95℃(6 h)，工况1拟合的温度峰值为55.40℃(11.5 h)，峰值差值为5.55℃，而工况2拟合的温度峰值为 61.13 ℃(6.5 h)，峰值差值为 0.18℃;TS-2实测的温度峰值为58.75℃(6.5 h)，工况1拟合的温度峰值为54.06℃(12 h)，峰值差值为4.69℃，而工况2拟合的温度峰值为59.63℃(7 h)，峰值差值为0.88℃;TS-3实测的温度峰值为61.75℃(5.5 h)，工况1拟合的温度峰值为55.80℃(11 h)，峰值差值为5.95 ℃，而工况2拟合的温度峰值为61.89℃(6 h)，峰值差值为0.15℃.后期各测点的温度随着龄期的增长，2种工况差异逐渐减小.

从温度峰值来看，2种工况下拟合的温度与实测值最大温差分别为5.95和0.88℃.工况1相对于工况2，最大温差增加了5.07℃.从达到温度峰值的时间上看，工况1达到温度峰值的时间比实测值要晚5.5 h左右，而工况2达到温度峰值的时间与实测值达到峰值时间相差不大.由此可知，工况1对温度场的模拟存在温度峰值偏低、温升速度偏慢的问题，其峰值温度低于实测峰值温度4.6℃以上，其达到峰值温度的时间要慢5 h以上，从防裂和温控角度看这样做是不合理的;在温度峰值上工况2的模拟结果略高于试验结果，但其误差仅为1.5%，达到温度峰值的时间误差控制在0.5 h之内，这对于整体温度场影响不大.因此对于早期温度场的精确模拟有必要考虑导热系数和比热容的变化过程，否则会导致对温度场的模拟存在温度峰值偏低、温升速度偏慢的问题，从而引起温度应力计算出现较大误差，导致采取不安全的抗裂和温控措施.

5 结语

早期混凝土温度场受环境温度、自身性能等多方面因素影响，因此对早期混凝土温度的模拟是一个复杂的非线性问题.本文通过采用不同的温度场模型对试验结果进行数值模拟，结果表明:考虑早期混凝土导热系数和比热容随水化度的变化过程，数值模拟结果与实测值基本一致，在量值上最大误差控制在1.5%以内，在时间上误差控制在0.5 h以内;当不考虑导热系数和比热容随水化过程的变化时，数值模拟与实测值存在较大误差，尤其是峰值温度及时间，峰值温度误差都在4.6℃以上，达到峰值温度的时间均相差5 h以上.由此可知，在对早期混凝土的温度场分析时有必要考虑早期混凝土导热系数和比热容随水化度的变化，不考虑这2个参数的变化会导致对温度场的模拟存在温度峰值偏低、温升速度偏慢的问题，从而导致不合理温控和抗拉的设计.

References)

[1] 朱伯芳.大体积混凝土的温度应力与温度控制[M].北京:中国水利水电出版社，1999:154-155.

[2] Demirboĝa R，Gül R.The effects of expanded perlite aggregate，silica fume and fly ash on the thermal conductivity of lightweight concrete[J].Cement and Concrete Research，2003，33(5):723-727.

[3] Uysal H，Demirboĝa R，Şahin R，et al.The effects of different cement dosages，slumps，and pumice aggregate ratios on the thermal conductivity and density of concrete[J].Cement and Concrete Research，2004，34(5):845-848.

[4] 苏敏.工程混凝土早期温度应力分析及二次开发的研究[D].哈尔滨:哈尔滨工业大学深圳研究生院，2010.

[5] Saul A G A.Principles underlying the steam curing of concrete at atmospheric pressure[J].Magazine of Concrete Research，1951，2(6):127-140.

[6] Azenha M，Faria R，Ferreira D.Identification of earlyage concrete temperatures and strains:monitoring and numerical simulation[J].Cement and Concrete Composites，2009，31(6):369-378.

[7] Lee Y，Kim J K.Numerical analysis of the early age behavior of concrete structures with a hydration based microplane model[J]. Computersand Structures，2009，87(17):1085-1101.

[8] 李骁春，吴胜兴.基于水化度概念的早期混凝土热分析[J].科学技术与工程，2008，8(2):441-445.Li Xiaochun，Wu Shengxing.Early-age concrete temperature analysis based on degree of hydration[J].Science Technology and Engineering，2008，8(2):441-445.(in Chinese)

[9] 陈长华.考虑钢筋作用的水工结构施工期温度场与温度应力分析[D].南京:河海大学土木工程学院，2006.

[10] Kim K H，Jeon S E，Kim J K，et al.An experimental study on thermal conductivity of concrete[J].Cement and Concrete Research，2003，33(3):363-371.

[11] Jeong J-H，Kim N.A thermal conductivity model for hydrating concrete pavements[J].Journal of the Korea Concrete Institute，2004，16(1):125-129.

[12] De Schutter G.Finite element simulation of thermal cracking in massive hardening concrete elements using degree of hydration based material laws[J].Computers and Structures，2002，80(27):2035-2042.

[13] Schindler A K.Concrete hydration，temperature development，and setting at early-ages[D].Austin，Texas，USA:University of Texas at Austin，2002.

[14] Van Breugel K.Simulation of hydration and formation of structure in hardening cement based materials[D].Delft，Netherlands:Delft University Press，1997.

[15] 崔溦，陈王，王宁.早期混凝土热学参数优化及温度场精确模拟[J].四川大学学报:工程科学版，2014，26(3):161-167.Cui Wei，Chen Wang，Wang Ning.Early concrete thermal parameters optimization and accurate thermal field simulation[J].Journal of Sichuan University:Engineering Science Edition，2014，26(3):161-167.(in Chinese)