容器壁厚度对光栅衍射法测量液体折射率的影响

张　静，满小溪

(东北师范大学 物理学院，吉林 长春 130024)

容器壁厚度对光栅衍射法测量液体折射率的影响

张静，满小溪

(东北师范大学 物理学院，吉林 长春 130024)

摘要：利用光栅衍射法测量了NaCl溶液的折射率，并分析了容器壁厚度引起的附加光程对折射率的影响. 采用折射率修正公式运用一级衍射得到的溶液的折射率更可靠.

关键词：折射率；光栅衍射；容器厚度

1引言

液体的物理性质主要包括液体的力学、光学、热学、磁学的性质[1]. 在液体的光学性质中，折射率是重要参量. 测量折射率的方法有很多，其中有基于迈克耳孙干涉仪测量液体折射率[2-3],基于等厚干涉原理测量液体折射率[4-5],利用CCD测量液体折射率等[6-8]. 本文通过光栅衍射法测量液体的折射率，并对玻璃容器自身厚度对折射率的影响进行了修正.

2实验的基本原理

2.1　光栅衍射法的实验

实验器材：光源采用波长为632.8 nm的氦氖激光器，样品池为长方形的玻璃容器，容器壁的厚度为2 mm，衍射光栅空间频率为300 mm-1，还有刻度尺、细线、铁架台等.

实验过程：

1)调节激光器的准直，可以借助平面镜对激光器的准直进行调节. 激光器发出的光打在平面镜上，缓慢地交替调节激光器的6个小螺丝，使通过平面镜反射回来的光束与激光器发出的光束重合，则此时激光器相对于玻璃容器准直.

2)激光器波长的校准. 首先通过光栅光谱仪对激光器的波长进行了校准. 由于汞灯谱线较窄，所以我们使用汞灯的绿色线进行定标，波长为632.8 nm.

3)向玻璃容器中注入溶液，将光栅置于溶液内，玻璃板后部的外侧贴1张半透明的纸，方便测量条纹.

4)开启光源，读取中心衍射斑，以及一级、二级和三级衍射斑的最亮光点的位置.

2.2　实验中容器壁所导致的误差分析

一般情况下，认为玻璃板很薄，所以在分析中会忽略玻璃板的厚度. 而实际上玻璃板的厚度对结果有一定的影响，因为玻璃板的折射率与液体的折射率不同. 在靠近激光器的玻璃槽的一侧垂直入射，因为光线不发生偏折，也不会引起光程的变化，可以不用考虑玻璃板厚度影响，但在光栅的后表面，激光照射到光栅上会让激光光束分成若干个光束，对经过光栅沿中心垂直出射的一束光不会有影响. 但是其他的光束因为不是垂直出射，射在玻璃板上就会发生折射，那么传播到玻璃槽后，原来沿着某方向偏折过来的光束就会有一定距离的平移发生，传播方向不变，但在接收屏上的位置会变化[9].

依据图1可以进行定性分析. 如果在处理数据过程中，不考虑有一定厚度的玻璃板造成的光束同方向平移，从屏上读到的点反向向衍射光栅做连线(图中虚线)，光的折射角度将偏小. 如此的数据处理，也即测量得到的液体折射率将偏小.

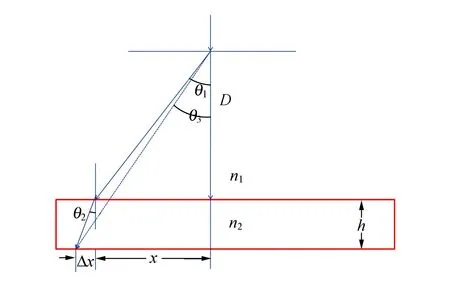
图1　容器壁对液体折射率测量造成误差的示意图

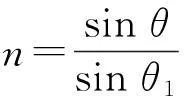
3误差的处理过程

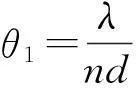
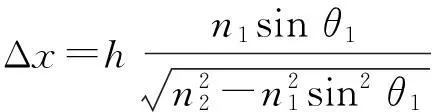
(1)

同理，

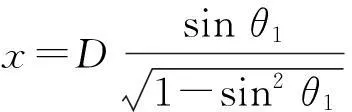
(2)

(3)

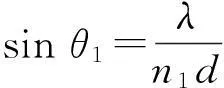
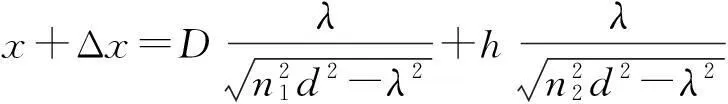
(4)

可以得到

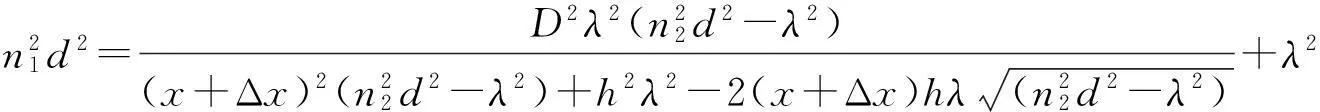
(5)

所以折射率为

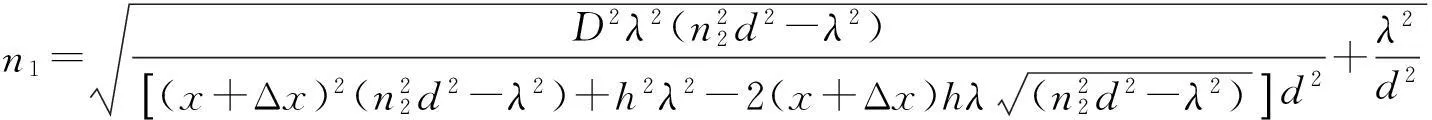
(6)

在实验中具体使用了2种质量分数的NaCl溶液(0.05，0.10). 根据测量数据分析由于玻璃板的引入对折射率的测量结果影响如表1所示.

表1质量分数为0.05和0.10的NaCl溶液(一级衍射条纹)的折射率

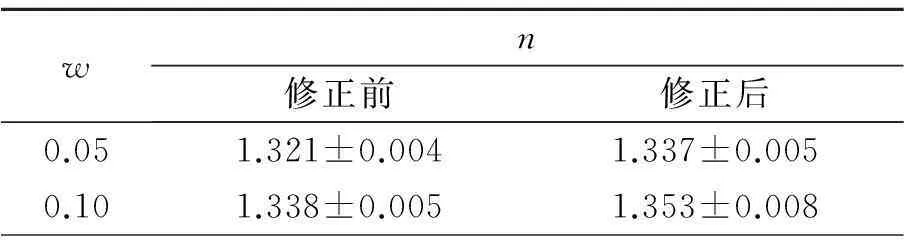
wn修正前修正后0.051.321±0.0041.337±0.0050.101.338±0.0051.353±0.008

表中“修正前”指的是没有考虑样品池玻璃厚度时，运用一级衍射得到的溶液的折射率. “修正后”为考虑玻璃厚度带来的附加性光程，对溶液的折射率进行的修正. 可以看出玻璃厚度的影响是不可忽略的.

上述实验分析中，所得到的折射率以及相应的不确定度结果都是基于一级衍射，而事实上高级衍射对折射率的测量值有一定的影响. 对NaCl的这2种质量分数的溶液进行了相应的测量和分析，得到高级衍射对折射率的分析结果有一定的修正，修正之后的的结果略微变大.

4结束语

光栅衍射法是大学物理实验中常见的测量物体折射率的方法，考虑实验的可操作性，就一定有容器的存在，进而带来了对光程的影响，造成测量值偏小. 本文对容器壁厚度带来的附加光程对折射率的测量值进行了修正，证实修正的数值更加可靠. 另外实验是基于室温条件下进行的，温度会对折射率测量有一定的影响[10].

参考文献：

[1]Sylvester-Hvid K O, Mikkelsen K V, Nymand T M, et al. Refractive index of liquid water in different solvent models [J]. J. Phys. Chem. A, 2005,109(5):905-914.

[2]柯金瑞. 利用迈克尔孙干涉仪测定液体折射率[J]. 物理实验，2000,20(2):10-11.

[3]王小怀，李卓凡，陈怀. 迈克耳孙干涉仪应用功能的扩展[J]. 物理实验，2012,32(3)：22-24.

[4]史彭，凌亚文，华中文. 摄像型等厚干涉实验仪器的研究[J]. 大学物理，2003,22(9)：27-28.

[5]郭军. 基于等厚干涉原理的液体折射率测定装置[J]. 大学物理，2010,29(4)：46-48.

[6]辛督强，朱民，解延雷，等. 测量液体折射率的几种方法[J]. 大学物理，2007,26(1):34-37.

[7]李雅倩，付献斌，周坤. CCD分段测量的光学位移测量系统[J]. 光学 精密工程, 2011,19(9):2036-2042.

[8]Lin Chern-sheng, Huang Jui-tsung, Wei Tzu-chi, et al. High speed and high accuracy inspection of in-tray laser IC marking using line scan CCD with a new caliburation model [J]. Optics & Laser Technology, 2011,43(1)：218-225.

[9]丁建华. 光栅实验的误差分析[J]. 苏州大学学报：工科版，2007,27(6)：64-65.

[10]Mohsen-Nia M, Modarress H, Rasa H. Measurement and modeling of density, kinematic viscosity, and refractive index for poly (ethylene glycol) aqueous solution at different temperatures [J]. J. Chem. Eng. Data, 2005,50(5):1662-1666.

[责任编辑：任德香]

Influence of container thickness on the refractive index of solution in the method of grating diffraction

ZHANG Jing, MAN Xiao-xi

(School of Physics, Northeast Normal University, Changchun 130024, China)

Abstract:The refractive index of NaCl solution was measured by using the method of grating diffraction. The influence of the additional optical path brought about by the thickness of the wall of the container on the refractive index was analyzed. It was shown that the refractive index of the solution given by the amended formulae was more reliable on the basis of the first order diffraction.

Key words:refractive index; grating diffraction; thickness of the container

中图分类号：O436.1

文献标识码：A

文章编号：1005-4642(2015)04-0034-03

作者简介：张静(1990-)，女，辽宁朝阳人，东北师范大学物理学院硕士研究生，研究方向为光学检测.

收稿日期：2014-12-01；修改日期：2015-02-28