基于RPROP神经网络的多模盲均衡算法研究*

吕大千 何 俊 李柔刚

(电子工程学院 合肥 230037)



基于RPROP神经网络的多模盲均衡算法研究*

吕大千 何 俊 李柔刚

(电子工程学院 合肥 230037)

针对传统盲均衡算法运算量大、收敛速度慢的问题,结合RPROP神经网络算法运算量小、速度快的优点,提出了一种基于RPROP神经网络的多模盲均衡算法。运用Matlab软件,以16QAM、16PSK信号为输入源,对该算法均衡效果进行仿真研究,仿真结果表明该算法在有效减少码间串扰的同时,缩短了收敛时间,达到了预期效果。

盲均衡; 多模算法; RPROP; 神经网络

Class Number TP183

1 引言

盲均衡技术是一种不借助训练序列,仅仅利用接收信号均衡信道特性的自适应均衡技术,主要用于消除码间干扰,在数字通信等领域有着广泛应用。多模算法(Multi-modulus Algorithm,MMA)是J. Yang等提出的一种盲均衡算法[1],该算法均衡效果好,算法收敛速度慢。文献[2～6]利用神经网络的方法对盲均衡算法进行改进,取得了一定效果,但无法克服收敛较慢的缺点。RPROP(resilient back-propagation)神经网络对传统神经网络算法的代价函数以及权值更新方式进行了改进,运算量小并且具备更快的收敛速度。本文在此基础上提出了一种基于RPROP神经网络的多模盲均衡算法。

2 多模算法(MMA)

多模算法(MMA)是在常模算法(CMA)[7]基础上提出的盲均衡算法,该算法的特点是尽量使输出信号聚集在星座图矩形区域的顶点上,由于算法充分利用了相位信息,有效减小了输出信号的相位偏转现象。其算法原理如图1所示。

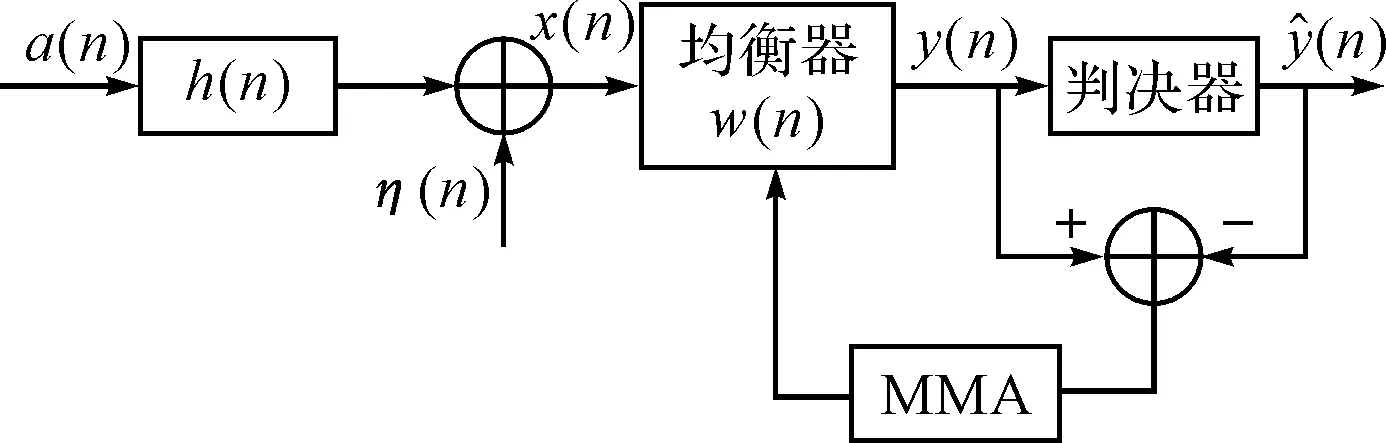
图1 多模算法示意图

γR=E{|aR(n)|2P}/E{|aR(n)|P}

γI=E{|aI(n)|2P}/E{|aI(n)|P}

其中,a(n)=aR(n)+jaI(n),表示经过调制后的输入信号。

由于常模算法用同一模值对信号进行处理,剩余误差较大。为避免单一模值对多模信号处理造成的较大误差,J. Yang提出了一个新的代价函数:

式中,下标R表示信号的实部;下标I表示信号的虚部。

在此代价函数基础上得到的误差函数为

根据最速下降法,推导得到修正常模算法抽头系数更新的迭代公式:

W(n+1)=W(n)+μ·eMMA(n)·X*(n)

式中,μ为步长因子,*表示共轭运算,通常P=2。

3 RPROP神经网络

RPROP神经网络是1993年德国学者Martin Riedmiller和Heinrich Braun提出的一种改进BP神经网络[8]。传统BP神经网络的权值更新易受偏导数大小影响,收敛速度较慢,并且容易陷入局部极小值。RPROP神经网络提出了新的权值更新方法,权值的更新由偏导数∂E(t)/∂wij的符号决定,避免了传统BP神经网络的上述问题,收敛速度更快。

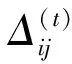
式中,t表示训练次数,η+为更新值增大倍数、η-为更新值缩小倍数,取值范围0<η-<1<η+。为了便于计算,减少可变参数的数量,η-、η+一般被设置为固定值,通常η+=1.2,η-=0.5。Δij的初始值一般为0.1,也可根据实际调整。

由此可得修正后的权值更新公式为

4 基于RPROP神经网络的改进多模盲均衡算法

Cybenco[10]证明了一个具有隐层的神经元结构能以任意精度逼近连续函数。从算法上看,RPROP神经网络算法简便,运算量小,实际应用性较强,适用于均衡器的训练。因此均衡算法改进思路为:先输入少量信号,采用RPROP神经网络对均衡器的权值进行训练,然后转入多模算法。

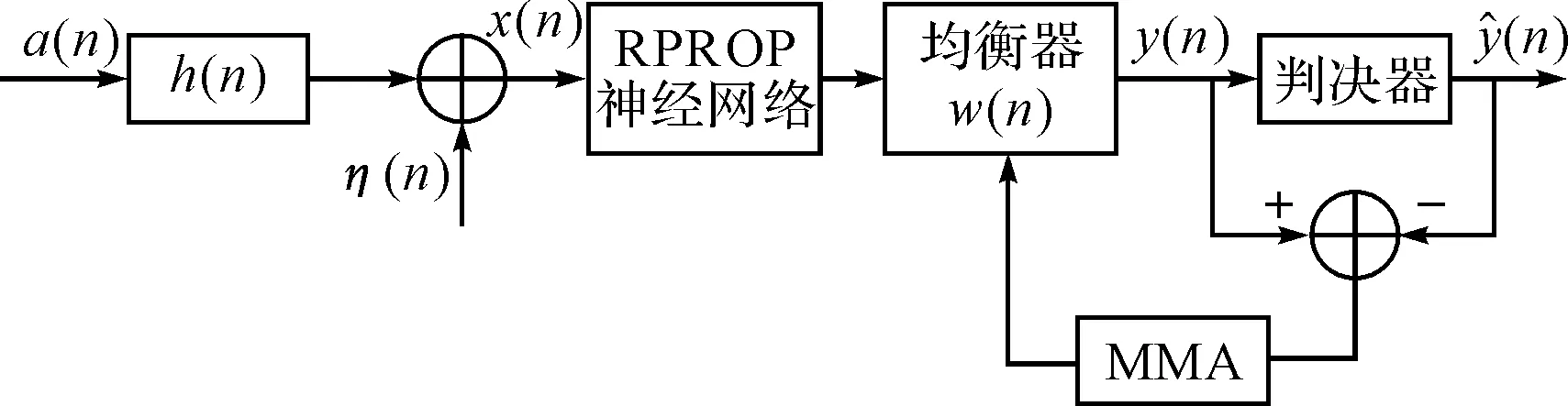
图2 基于RPROP神经网络的多模算法示意图

当n≤15时,以J(n)为代价函数,运用RPROP神经网络对均衡器权值进行训练。

当n>15时,转入多模算法,代价函数仍然为

利用训练好的权值进行信号处理,同时继续更新均衡器的权值:

W(n+1)=W(n)+μ·eMMA(n)·X*(n)

5 仿真验证与性能分析

为了检验改进算法的性能,分别对多模算法、基于RPROP神经网络的多模算法进行仿真验证,仿真条件为:发射信号分别采用16PSK、16QAM调制,均衡器抽头数为12,数据长度为12000,信噪比为25dB,信道噪声为加性高斯白噪声。信道传递函数为:h=[0.005 0.009 -0.024 0.854 -0.218 0.049 -0.016],步长μ=0.002。MMA算法初始化时,采用中心置1法。神经网络学习率lr=0.05,迭代次数epochs=300,误差目标值goal=10-3。隐含层、输出层的传递函数分别为tansig、purelin,学习函数为trainrp。仿真结果如图3、图4所示。

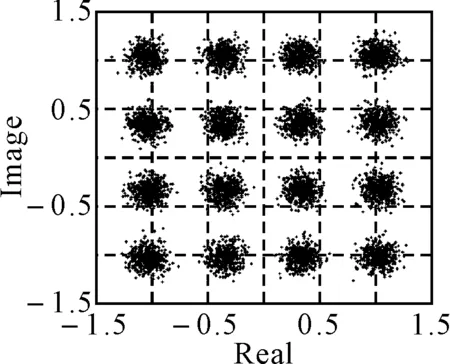
从图3、图4可以看出,改进后算法的均衡效果明显得到改善,码间干扰明显减小,在一定的门限电平下,原始编码信号可以得到较好的恢复。

图5 MMA均衡16QAM信号的均方误差

图6 RPROP-MMA均衡16QAM信号的均方误差

图7 MMA均衡16PSK信号的均方误差

从图5～图8可看出,较传统多模算法,改进后的多模算法稳态误差减小,收敛速度加快。另外,从图6与图8的对比中可以看出改进后的多模算法在处理16QAM信号时,均衡效果更好,这主要是因为多模算法的代价函数是以星座图中信号距离矩形区域顶点的距离最小为检测标准,与QAM信号在星座图中呈矩形格状的分布方式比较一致,因而均衡处理速度更快。

图8 RPROP-MMA均衡16PSK信号的均方误差

6 结语

本文首先介绍了多模算法与RPROP神经网络及其优缺点,并在此基础上提出一种基于RPROP神经网络的多模盲均衡算法。仿真结果表明,改进后的多模算法性能更好,稳态误差较之前也有所减小。此外,RPROP神经网络由于算法简单且计算量小,便于工业应用。改进后的多模算法在运算量较大的信号均衡处理中,有着较强的实用价值。

[1] J. Yang, J. J. Werner, G. A. Dumont. The multimodulus blind equalization algorithm[C]//13th International Conference on DSP,1997,7(1):127-130.

[2] N. Benvenuto, M. mar. esi, F. Piazza, et al. nonlinear satellite radio links equalized using blind neural networks[C]//Proc.IEEE ICASSP,1991,50:1521-1524.

[3] G. Kechriotis, E. Zervas, E. S. Manolakos. Using recurrent neural network for adaptive communication channel equalization[C]//IEEE trans on. Neural Network,1994,5(2):267-278.

[4] 梁启联,周正,刘泽民.基于递归神经网络的盲均衡算法的改进[J].北京邮电大学学报,1997,20(4):6-11.

[5] 肖瑛,李振兴,董玉华.动态目标函数下的神经网络盲均衡仿真研究[J].系统仿真学报,2009,21(14):4331-4334.

[6] 刘莉.基于神经网络盲均衡优化算法的研究[D].南京:南京邮电大学硕士论文,2012.

[7] Godard D N. Self-recovering equalization and carrier tracking in two-dimensional data communication systems[J]. IEEE Trans on Communications,1980,28:1867-1875.

[8] Riedmiller M, Braun H. A direct adaptive method for faster back-propagation learning The RPROP algorithm[C]//IEEE International Conference on Neural Networks,1993,9:586-591.

[9] 张治国.RPROP算法在测井岩性识别中的应用[J].吉林大学学报( 地球科学版),2005,35(3):389-393.

[10] Cybeaco G. Approximations by superposition of a sigmodal function[J]. Math Contr Syst Signals,1989,2:303-314.

Research on Multi-modulus Blind Equalization Algorithm Based on RPROP Neural Network

LV Daqian HE Jun LI Rougang

(Electronic Engineering Institute, Hefei 230037)

Aiming at the problem of traditional blind equalization algrithm’s high computation and slow convergence,considering the advantages of resilient back-propagation(RPROP) Neural Network’s low computation and quick convergence, a kind of Multi-modulus Blind Equalization algorithm based on RPROP neural network is proposed. By using Matlab, considering 16QAM and 16PSK signals as input source, the equalization’s effects are studied. The result of simulation indicates that this algorithm can efficiently eliminate the intersymbol interference and reduce time of convergence. And it meets the expectations.

blind equalization, multi-modulus algorithm, Resilient Back-propagation, neural network

2015年6月3日,

2015年7月27日

吕大千,男,硕士研究生,研究方向:数字通信。

TP183

10.3969/j.issn.1672-9730.2015.12.012