多阶段数量折扣订货模型优化与遗传算法求解*

孙方东 李宗吉

(1.91183部队 青岛 266102)(2.海军工程大学兵器工程系 武汉 430033)



多阶段数量折扣订货模型优化与遗传算法求解*

孙方东1李宗吉2

(1.91183部队 青岛 266102)(2.海军工程大学兵器工程系 武汉 430033)

针对现有订货批量模型在描述库存成本上的缺陷,对其进行了修正。应用遗传算法对修正后的模型进行了求解,结合动态规划最优性原理,着重优化了遗传算法编码方案的设计,确保编码方案的完备性。经实例验证,该求解方法可有效解决多阶段数量折扣问题,克服了动态规划和S-M法的局限性。

遗传算法; 数量折扣; 订货策略

Class Number TP18

1 引言

供应商为刺激消费需求,减少产品积压,加速资金流转,通常会提供数量折扣,即购买商品的数量不同,商品单价也不同,一般情况下购买数量越多,单价越低。在这种情况下,从买方的角度,就需确定其经济合理的订货策略使其成本降低。这是一类典型的动态批量问题,其求解的基本思路是建立描述具体问题的线性或非线性规划模型,并运用一定的算法求解。现有的规划模型[5～8]结构均比较相似,但存在对目标函数中库存成本表达不完善的缺陷。

求解算法中比较常用的是Sliver&Meal启发式算法(S-M)、拉格朗日松弛解法、动态规划法(DOQ)和启发式算法[2]。文献[3～4]虽指出S-M法有可能收敛到局部最优,并提出了各自的解决方案,但并未从根本上解决此问题。DOQ模型基于对最优解结构属性的证明,大大缩小了可行解的空间范围,是求解动态批量问题的最核心和基础的方法,但DOQ模型对目标函数和约束条件及问题背景均有一定要求[2]。且随着多级多项目多资源问题的引入,动态规划作为精确求解方法很难在短时间内取得满意解。

本文首先修正了现有模型中库存成本的表达式,使其更符合实际情况,进而应用遗传算法对模型进行了求解。基于该类问题最优解的性质[8],结合动态规划最优性原理,着重优化了遗传算法编码方案的的设计,确保编码方案可遍历各可行解,进而收敛到全局最优。结合文献[4,7]中的两个案例,进行了实例计算,计算结果表明,本文提出的优化算法有更好的效果。

2 模型建立

订货批量问题属于多周期规划问题,将规划期分成不同的时间周期,基于不同周期的需求,综合权衡购买成本、订货准备成本和库存成本。优化目标为在恰当的时间购买恰当数量的产品,使相关总成本最小。设周期性检查库存,只在期初订货,其订货量为xi,提前期固定,不允许缺货。计划时段为n个周期,计划期开始时和结束时库存都为零。成本包括购买成本、订货成本和库存成本。已有文献[5～8]在建立该问题的模型时,目标函数多采用如下所示的形式:

(1)

式(1)中及下文将用到的各符号代表的物理意义如表1所示。

表1 各符号物理意义

目标函数中第一项为购买成本,第二项为库存管理成本,第三项为订货成本。考察式(1)中的库存管理成本,该表示方法规定了库存管理成本仅由期末剩余的库存所决定,而没有考虑逐步消耗的备件同样会带来管理成本,这显然是不合理的。考虑一个极端情形,设第i时间段开始时的订货在期末恰好用完,该时间段库存Ii=0,则库存管理成本为零,显然不符合实际。因此用hi·Ii计算库存管理成本是不合适的。

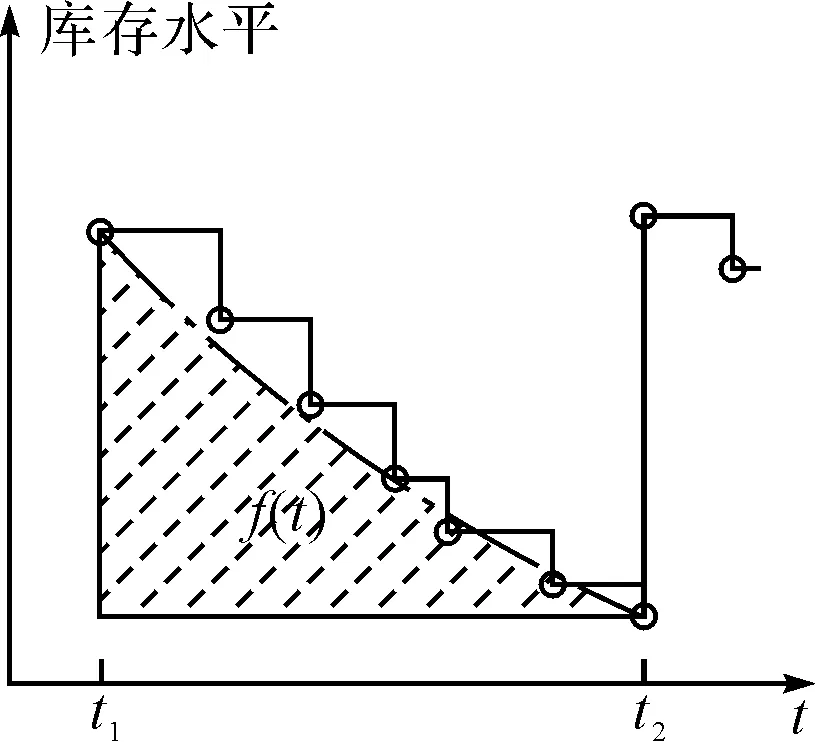
图1 物资消耗过程

考察物资消耗过程如图1所示。

(2)

考虑一种较特殊的情形,备件消耗速度不变,这在短周期内是可以接受的。设第i时间段内需求为di,则由需求引起的平均库存为di/2,加上未消耗完的库存即为该时间段的总体平均库存水平,库存成本为hi·(Ii+di/2),本文即在该种情形下建立模型。

（1）无双重支付的情形。假设A有1枚比特币，要将其转给B。A首先构造一笔交易Tx1：使用私钥签署该笔交易，并将交易单Tx1广播出去。其他实体收到信息后，通过UTXO索引计算A是否有能力支付1枚比特币，如果有能力支付，则认为此次交易是合法。最后，A的钱包地址减少1枚比特币，B的钱包地址增加1枚比特币。

重新建立模型如下:

Ii=Ii-1+xi-di

∑xi=∑di

(3)

订货序列x={xi,i=1,2,…,n}即为决策变量。

3 算法设计

1) 最优解的性质

2) 应用遗传算法求解的思路

遗传算法的操作对象是与决策变量相对应的编码,问题的关键在于选取合适的操作变量,构造合理的编码方案,使得编码方案具有完备性和非冗余性,即遗传算法空间中的染色体能对应所有问题空间中的候选解,并尽可能缩小寻优空间。文献[6]提出将每期的订货量作为操作变量,采用实值编码方案。该方案物理意义明确,但问题实质上是只有第一期和最后一期为再生点的特殊情况。同时产生随机个体的方法会产生大量无意义的冗余方案,造成了计算资源的浪费。文献[7]将Y(xi)作为操作变量,采用二进制编码。不存在折扣时,Y(xi)与订货量存在一一对应的关系,可以方便的进行转化,不失为一种具备完备性和非冗余性的好方法。本文中的第一个案例,即采取该方案得到了理想的结果。但存在折扣时,决策变量订货量有可能是折扣点,也有可能是实际需求量,与Y(xi)没有一一对应关系,因此该编码方案不能解决存在折扣的问题。其提出的案例虽然带有折扣,但实际按照无折扣进行近似优化,得到的结果不一定是最优。本文在实例计算中对其中的一个案例进行重新优化,得到了更为理想的结果。

本文的编码方案如下:

设有两个相邻的再生点Zj、Zk,构造算法如下:

Step 1:i=1:length(j+1:k)

if length(j+1:k)=1,则j+1期订货量为实际需求量;

if length(j+1:k)>1,进入step 2;

Step 2:按照带折扣问题可行解的性质,对每一阶段产生一个可行解矩阵,代表该阶段所有的子策略。可行解矩阵每一行为一个可行解,其中第一行可行解的最后一次订货小于最小的折扣点,则第l行可行解的最后一次订货是第一行可行解最后l次订货量之和。以某一阶段中有三个订货点为例,可能的可行解矩阵结构如下所示:

其中x1、x2、x3是三个订货量不为零的订货点,订货点的订货量须满足最优解性质。此时问题的关键为如何实现第一行解的构造,本文中第一行可行解的产生程序框图如图2所示。

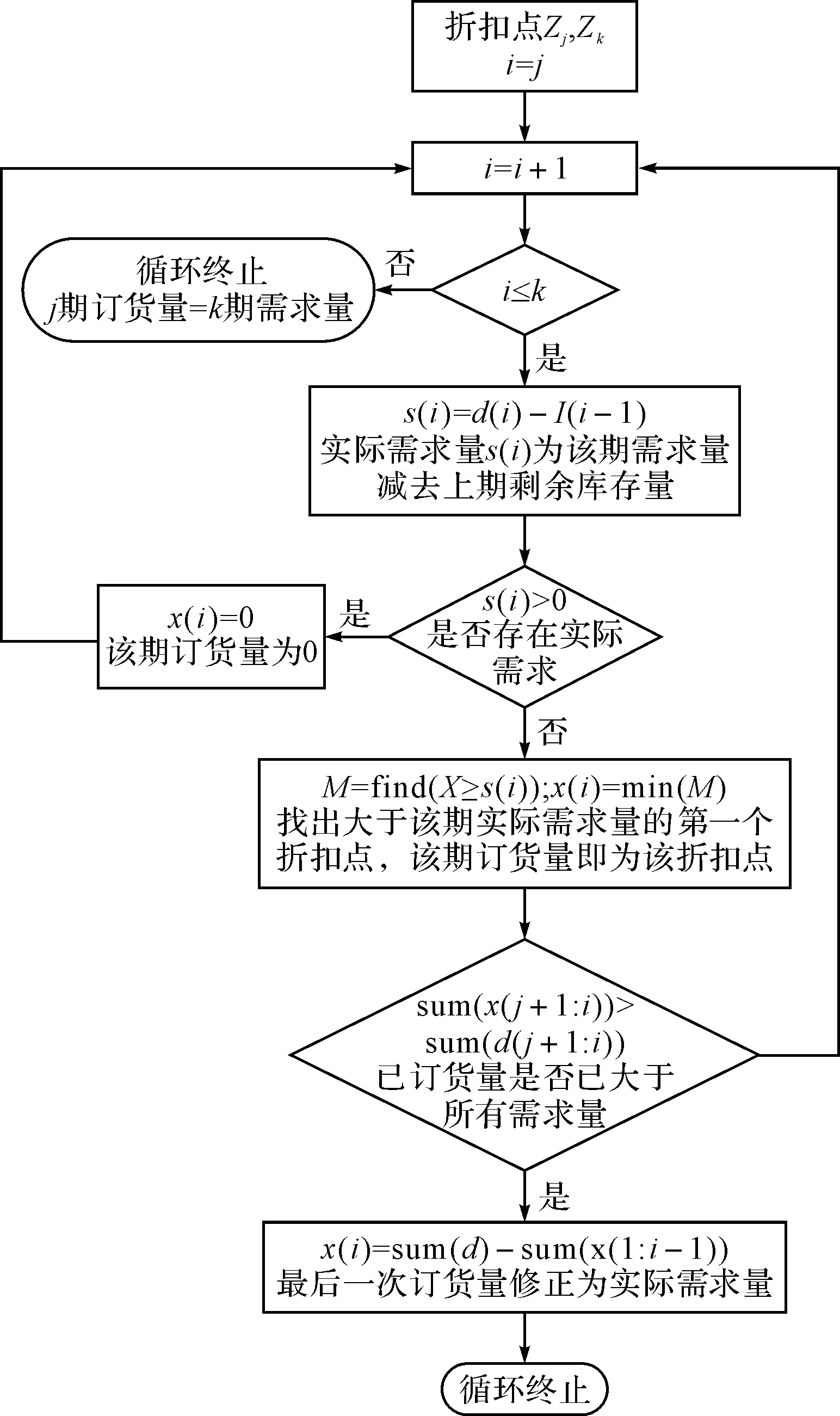
图2 第一行解产生程序框图

4 实例计算

例1首先考察无折扣时的优化策略,取文献[4]中应用S-M法优化订货策略的案例,简便起见,仅取其数据,并去掉量纲。其需求数据如表3所示,其中订货费用为1200,储存费用为50。

表3 物资需求数据

分别应用动态规划和遗传算法进行优化,计算结果如表4所示。

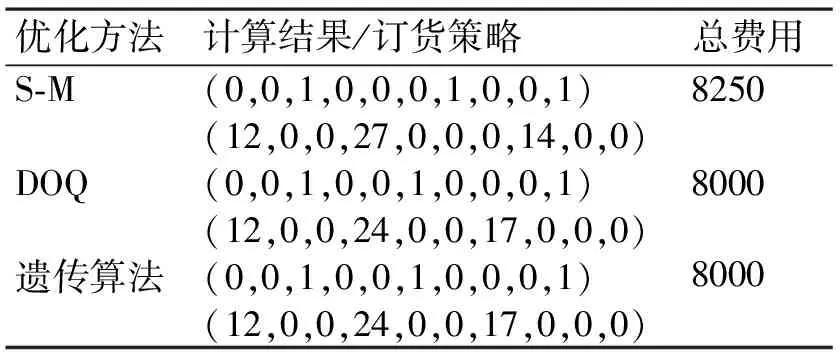
表4 订货策略优化结果

DOQ及遗传算法优化策略的到货点在周期1、4、7,订货数量分别为12、24、17,得到总成本费用为8000。S-M法得到的优化策略到货点分别为1、4、8,订货数量分别为12、27、14总成本费用为8250。说明本文提出的方法不仅是有效的,而且优于S-M法,能收敛到全局最优。

由于带折扣问题涉及多个变化的参数,状态空间庞大,难以采用动态规划法验证本文提出的方法是否收敛到全局最优,故本节选取文献[7]中案例,对同一案例进行优化,进而比较两者结果。

例2取文献[7]中的案例,同样取其数据,去掉量纲。其中产品1的需求为[50,45,35,60],折扣点为[100,300],单价分别为[12,10,8],订货成本分别为[10,11,12,10],储存成本为[0.5,0.4,0.6,0.5]。文献[7]中的方法一与本文提出的方法二计算结果对比如表5所示。

表5 计算结果对比

可以看到,本文提出的方法得到的总费用较少。进一步分析结果,本文的计算结果导致一次性大量订货,观察储存成本与单价,发现产品1的储存成本仅占单价的5%,一次性大量订货是可以接受的,若考虑其他资源的约束,如资金、库存容量等限制,则要另外建立模型加以分析,就本案例,本文提出的解决方法是较优的。

5 结语

本文首先对带折扣批量订货问题模型进行了修正,使其更符合实际情况。进而基于该类问题最优解的性质,应用遗传算法对该问题进行了求解,结合动态规划最优性原理,着重优化了编码方案的设计,确保算法可收敛到全局最优。同时遗传算法作为启发式算法,在求解大型问题时比动态规划法有更好的寻优速度。此外,遗传算法构造简单,可方便地进行拓展以解决更复杂的问题。计算结果也验证了本文提出的方法的有效性,可对工程实践给予指导。

[1] 徐健腾,张庆普.多供应商的动态批量问题研究[J].哈尔滨工程大学学报,2010,31(4):451-456.

[2] 王海英,等.基于动态规划方法的动态批量问题研究[J].科技进步与对策,2009,26(4):162-165.

[3] 金锡万.多阶段需求不均衡时的一种库存控制模型-兼评Silver&Meal启发式算法I[J].物流技术,1995(6):15-18.

[4] 唐纳德·沃尔特斯著.李习文,李斌译.库存控制与管理[M].北京:机械工业出版社,2005:82-86.

[5] 唐立新,杨自厚,王梦光,等.CIMS中带多资源的CLSP问题的遗传启发式算法[J].系统工程理论与实践,1997(4):39-44.

[6] 王建忠,杜纲.基于遗传算法的数量折扣订货模型求解[J].河北工业大学学报,2006,35(2):81-85.

[7] 田俊峰,杨梅.数量折扣条件下的动态订货批量优化[J].西南交通大学学报,2004,39(5):595-599.

[8] 徐健腾,张庆普.多供应商的动态批量问题研究[J].哈尔滨工程大学学报,2010,31(4):451-457.

[9] Shittu, E. (2003). Applying genetic algorithms to the deterministic time-varying fixed quantity lot sizing problem[D]. Masters Thesis. Cairo, Egypt: The American University in Cairo.

[10] Lotfi Gaafar. Applying genetic algorithms to dynamic lot sizing with batch ordering[J]. Computers & Industrial Engineering,2006(51):433-444.

Optimization for Multi-period Ordering Model with Quantity Discount and Solving Based on GA

SUN Fangdong1LI Zongji2

(1. No. 91183 Troops of PLA, Qingdao 266102) (2. Naval Research Institute of New Weaponry Technology & Application, Naval University of Engineering, Wuhan 430033)

The model describing the ordering problem with quantity discount is modified to be true of the reality. And a method was proposed based on Genetic Algorithms, especially the coding method is optimized to get the best result. Using certain numerical examples, the method is proved to be effecter than S-M and DOQ.

GA, quantity discount, order tactics

2015年6月11日,

2015年7月26日

孙方东,男,助理工程师,研究方向:水中兵器动力推进技术。

TP18

10.3969/j.issn.1672-9730.2015.12.031