一种水下体目标回波信号的高精度频率估计方法*

刘演龙 石钊铭

(海装重庆局 重庆 401100)



一种水下体目标回波信号的高精度频率估计方法*

刘演龙 石钊铭

(海装重庆局 重庆 401100)

针对鱼雷声引信工作区域内目标回波的体目标效应对回波信号的多普勒频率估计精度的影响,提出了一种幅度比值-分段相位差联合频率估计方法(简称RP方法)。该方法将传统的Rife算法和分段相位差算法相结合,通过对所估计的信号频率进行预处理,在不同的频段采用不同的估计算法,使算法的整体性能显著提高,充分保留了两种算法的优点,同时又克服了各自的缺陷,实现了对目标回波信号多普勒频率的高精度估计。仿真结果表明,该方法估计精度高且稳定性较好,能够较好地满足鱼雷在声引信工作区域内提取目标回波多普勒频率信息,实现精确炸点预测,具有一定的工程应用价值。

水下体目标; 频率估计; Rife算法; 分段相位差算法

Class Number TJ630.2

1 引言

鱼雷攻潜过程中,由于声引信的工作区域内目标回波呈现出明显的体目标效应,鱼雷主动声引信脉冲的回波信号含有丰富的多普勒信息。通过分析该回波的多普勒信息,鱼雷就可以获得目标的相对速度和相对距离等特征信息,有效确定引信炸点位置,提高命中概率。

由于鱼雷速度高,主动声引信回波信号含有多频率成分,为了准确估计出多普勒频率,国内外有许多专家提出了一些高精度频率估计方法。例如,多重信号分类算法(MUSIC)、子空间旋转不变技术(ESPRIT)等现代谱分析方法。这些方法虽然分辨率高,但运算量大,不利于实时处理[1～6]。而传统的FFT直接谱估计方法虽简便、计算量小,实时性好,但估计精度依赖于采样数据长度N,且存在能量泄露和栅栏效应,导致该方法误差较大。为了提高FFT算法的精度,齐国清[7]提出了一种插值FFT算法,该算法对幅频图主瓣内最大的2条谱线进行插值,以提高基于FFT的频率估计精度,但当信号频率位于量化频率附近时,会因为差值方向错误导致频率估计误差增大。此外,齐国清[8]还提出利用信号的初相位信息提高FFT的频率估计精度,但当最大谱线对应的频率相对误差比较大时,容易产生相位模糊,从而增大频率估计误差。

针对应用背景,本文结合Rife算法和分段相位差算法的思想,提出了一种幅度比值-分段相位差联合频率估计方法(Rife-Segmented Phase Difference Method,RP),实现了对水下体目标回波信号多普勒频率的高精度估计。

2 目标回波信号模型

目标回波信号是声自导鱼雷对目标进行检测、参数估计和识别的基础。在高频情况下,任何一个水下体目标的回波信号都是由若干个子回波信号叠加而成,而每个子回波信号都可以看作是由某个散射点发出的,该散射点在工程应用上称为亮点[9]。

理论分析和实验结果证明,目标回波信号有三个重要属性:亮点起伏、时间展宽、空间方位分布。因此,一个完整的目标回波信号模型由幅度因子、时延、和相位跳变三个参数决定[10～12]。从而对于单个亮点,其传递函数可表示为

H0(r,θ,ψ,ω)=A0(r,θ,ψ,ω)ejωτ0ejφ0

(1)

式中,A0(r,θ,ψ,ω)为该亮点回波信号的幅度,其值由鱼雷到该亮点的距离r、方位角θ、俯仰角ψ、ω为回波的中心频率与入射声波的中心频率之间的多普勒频移四个参量确定;τ0为该亮点的时延,由等效散射中心相对于某参考点的声程决定;φ0为回波形成后的相位跳变。

因此,一个N亮点目标的传递函数为

(2)

若鱼雷发射单频矩形脉冲信号为

s(t)=a(t)e-j2πf0t

(3)

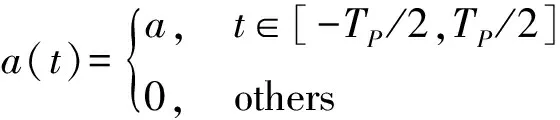
假设鱼雷发现某水下目标,由于该目标的散射波以ejkr/r的规律扩展[4],k为波数;同时,鱼雷已定身在该目标大致深度上,即俯仰角φ可近似为0。因此,该回波信号为

(4)

式中,ωd为目标和鱼雷相对运动产生的多普勒频移量;由于鱼雷在运动过程中已经对自身进行了多普勒补偿,因此只需考虑目标产生的多普勒频移,即

ωd=2ωcνcosθ/c

(5)

式中,ν为目标航速;c为水中声速。

将式(5)代入式(4),得到目标回波信号的时域表达式:

(6)

3 回波信号频率估计方法

在水声信号处理工程应用中,固定水域、固定时间段的水声环境,其传播特性,如声速传播曲线、声速分布和信号的多普勒频移等,可认为是恒定的。因此,结合式(6),可以得到鱼雷在发现目标后,自导接收机接收的信号模型为

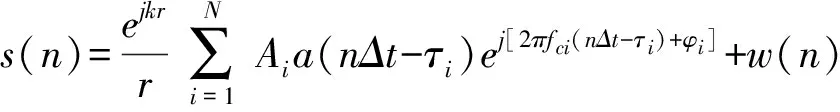
n=1,2,…,M-1

(7)

fci=f0(1+2νcosθi/c)

(8)

式中,fci为接收各亮点回波信号的频率;M为采样点数;Δt=T/M为[0,T]时间内的采样间隔;w(n)为高斯白噪声序列。

在实际应用中,为简化模型,把目标视为典型三亮点模型[11],则式(7)可化为

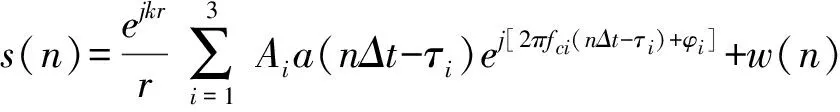
n=1,2,…,M-1

(9)

对于式(9)中任一频率成分fci的接收信号x(n),令x(n)的M点FFT为X(k),由于FFT频谱具有对称性,只考虑离散频谱的正频率成分,则

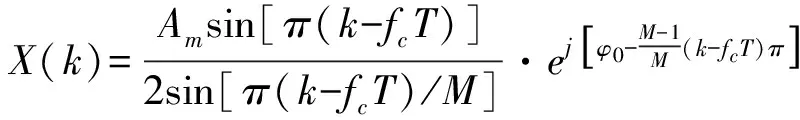
k=0,1,2,…,M/2-1

(10)

式中,Am为接收信号x(n)的幅度;φ0为接收信号x(n)的相位;fc为fci的频率值。

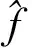
(11)

(12)

式中,k1为FFT最大谱线位置的索引号;|X(k1)|为X(k)的最大谱线幅值;|X(k1+α)|为X(k)的次大谱线幅值。当|X(k1+1)|≥|X(k1-1)|时,α=1;当|X(k1+1)|≤|X(k1-1)|时,α=-1。Δf1为N点FFT的频率分辨率,即Δf1=1/T。

分段相位差频率估计算法

由式(10)可知,X(k)的幅值最大处的相位可近似表示为

φm=φ0-(m-fcT)=φ0+πδ1

(13)

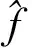
(14)

(15)

式中,k2=[fcT/2]为信号FFT幅度最大值处对应的离散频率索引号;δ2为相位差频率估计算法中的相对频率偏差。Δf2为N/2点FFT的频率分辨率,即Δf2=2/T。

根据两种算法的优缺点,本文将两种算法结合,通过与直接FFT的频率估计值进行比较,并根据不同的比较结果确定在不同的频段采用不同的估计算法,该方法既充分保留了两种算法的优点,又克服了各自的缺陷,使算法整体性能提高。

RP方法思路如下:

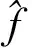
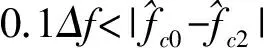
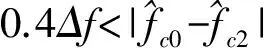
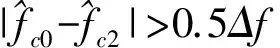
4 仿真实例

如图1所示,假设鱼雷捕获目标时与目标水平距离为L0=30m,鱼雷速度为vt=25m/s,目标速度为vs=6m/s,海水声速为1500m/s,载频fc为300kHz,采样频率fs为1.2MHz,样本点数为1024,进行1000次蒙特卡罗仿真,得到信噪比为3dB条件下,RP算法得到的频率估计平均值,如图2所示。

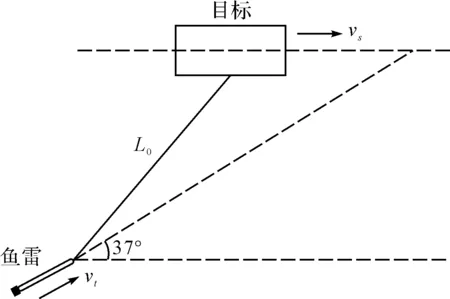
图1 鱼雷攻击目标示意图

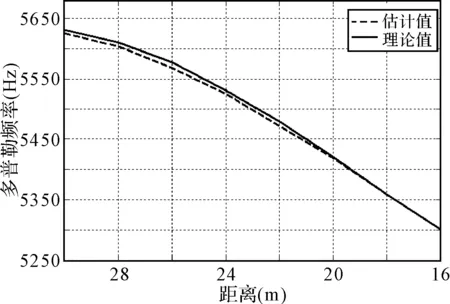
图2 多普勒频率随距离变化曲线

由图2可得,鱼雷向目标靠近时,RP方法的估计的多普勒频率平均值接近于理论值,从而证明该算法的正确性和有效性。

5 精度分析

根据参数估计理论,在给定数据长度和信噪比前提下,高斯白噪声背景下信号参数的任一无偏估计方差不会小于某一确定值,即CramerRao下限(简称CRLB)[13]。因此,CRLB可作为衡量频率估计算法精度的标准。对于复正弦波信号,有

(16)

根据文献[7],Rife算法的频率估计均方误差为

(17)

式中,erfc()为补误差函数。

根据文献[8],分段相位差估计算法的频率估计均方误差为

(18)

在SNR分别为-6、0、6dB时,分别采用Rife算法、分段相位差估计算法和RP算法对实例中信号进行频率估计,令ft=fc+δΔf,δ在[-0.5,0.5]取值均匀分成11个量化频率点,对每个频率点作1000次模特卡罗仿真,得到各算法的均方根误差曲线如图3所示。

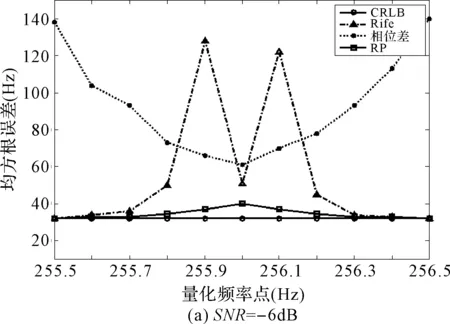
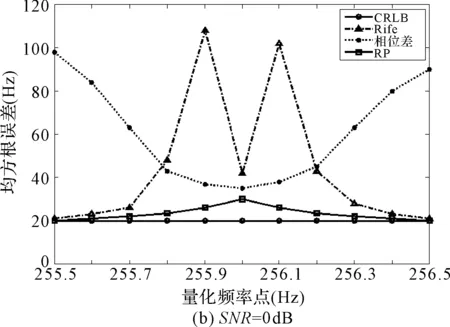
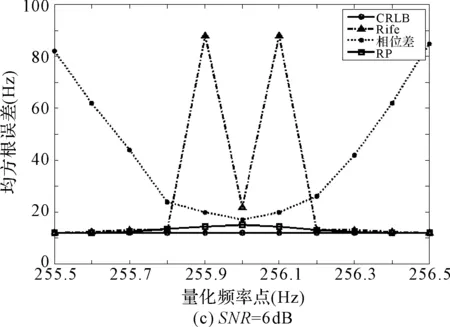
图3 Rife算法、分段相位差频率估计算法和RP算法在SNR=-6dB、0dB、6dB时的均方根误差曲线

由图3知,当|δ|较小时,Rife算法的估计误差较大;当|δ|较大(接近0.5)时,由于相位模糊问题,分段相位差算法的估计误差较大;在-6dB、0dB、6dB三种不同的信噪比条件下,RP方法在整个量化频率区间内的估计误差较小,且信噪比越大,估计误差越接近于CRLB。因此,RP方法的估计精度明显高于Rife算法和分段相位差算法。

在信噪比为-5dB到5dB的范围内,取N=1024,fc=300kHz,fc=300kHz,fs=1.2MHz,在每隔1dB的信噪比条件下,对三种算法进行1000次蒙特尔卡罗仿真,得到频率估计均方根误差曲线如图4所示。

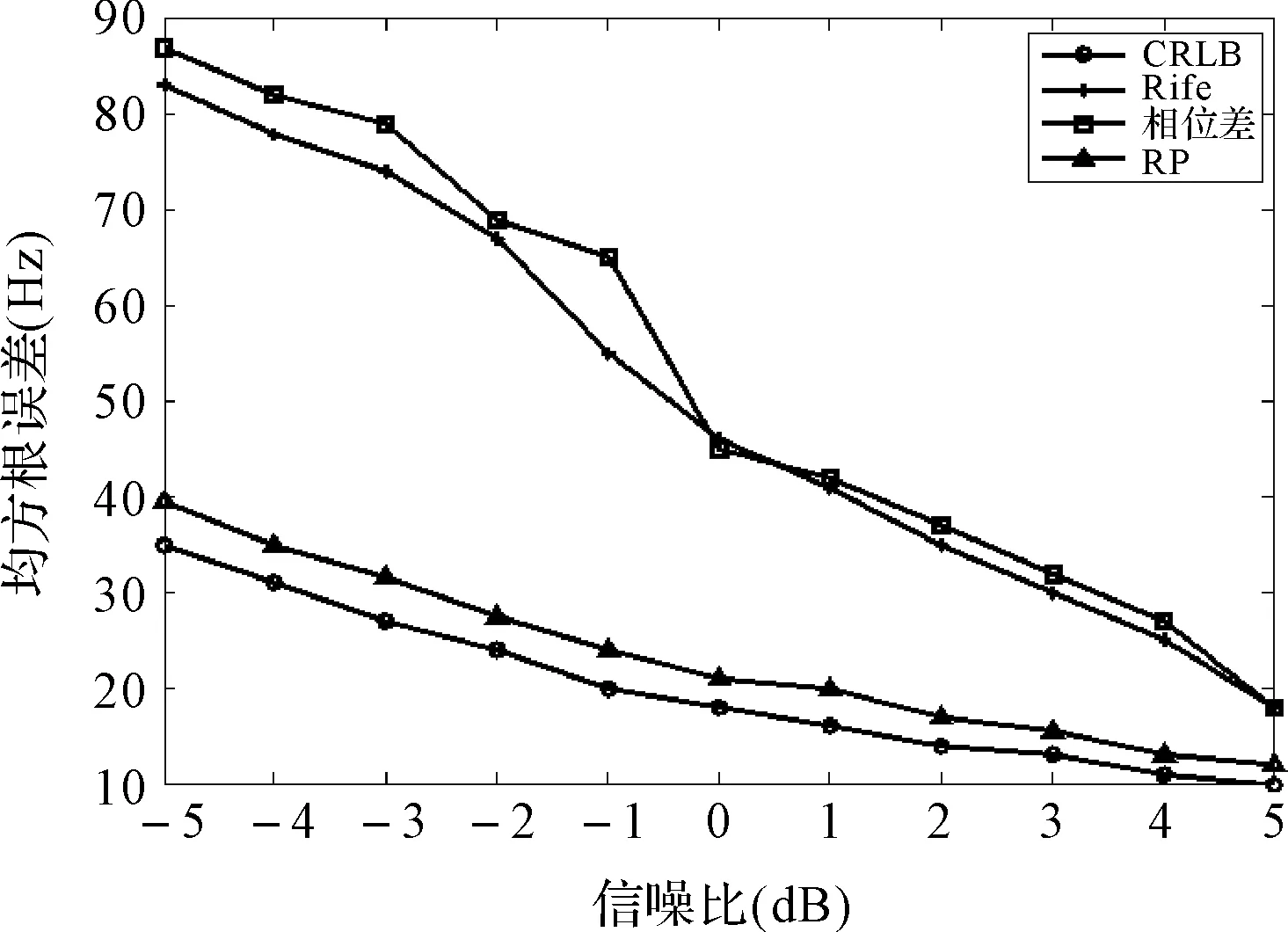
图4 均方根误差与信噪比的关系曲线

由上图可知,RP方法在较宽的信噪比条件下均能保持较低的均方误差,能够较好地满足鱼雷在声引信工作区域内提取目标回波多普勒频率,并准确估计目标距离,实现精确炸点预测,最大程度毁伤目标。

6 结语

针对鱼雷在声引信工作区域内体目标效应对回波信号的多普勒频率估计精度的影响,提出了RP方法,实现高精度提取目标回波多普勒频率信息。该方法将传统的Rife算法和分段相位差算法相结合,通过引入频率预处理,在不同的频段采用不同的估计算法,使算法的整体性能显著提高,充分保留两种算法的优点,同时又克服了各自的缺陷,实现了对目标回波信号多普勒频率的高精度估计。仿真结果表明,该方法估计精度高且稳定性较好,具有一定的工程应用价值。

[1] 刘银恩.高精度平频率估计算法研究[D].南京:南京理工大学,2007.

[2] Saman S. Abeysekera. Effcient Frequeney Estimation Using the Pulse-Pair Method at Various Lags[J]. IEEE Transactions on Communications,2006,54(9):16-26.

[3] Rife D C, Vincent G A. Use of the discrete Fourier transform in the measurement of frequencies and levels of tones[J]. Bell SysTech J,1970,49(2):197-228.

[4] Jane V K, Collins W L, Davis D C. High-accuracy analog measurements via interpolated FFT[J]. IEEE Trans. IM,1979,28(2):112-116.

[5] Quinn B G. Estimating frequency by interpolation using Fourier coefficients[J]. IEEE Trans-SP,1994,42(5):1264-1268.

[6] Quinn B G. Estimating frequency, Amplitude and Phase from the DET of a Tine Series[J]. IEEE Trans-SP,1997,45(3):814-817.

[7] 齐国清,贾欣乐.插值FFT估计正弦信号频率的精度分析[J].电子学报,2004,32(4):625-629.

[8] 齐国清.利用FFT相位差校正信号频率和初相估计的误差分析[J].数据采集与处理,2003,18(1):7-11.

[9] 汤渭霖.声纳目标回波的亮点模型[J].声学学报,1994,19(2):92-100.

[10] 何心怡,蒋兴舟,林建域.基于亮点模型的潜艇回波仿真[J].鱼雷技术,2001,9(3):15-18.

[11] 王明洲,黄晓文,郝重阳.基于声学亮点特征的水下目标回波模型[J].系统仿真学报,2003,15(1):21-25.

[12] 董忠臣,李亚安,陈晓.一种基于亮点模型的潜艇回波仿真方法[J].计算机仿真,2013,30(6):38-41.

[13] 齐国清.几种基于FFT的频率估计方法精度分析[J].振动工程学报,2006,19(1):86-92.

A High Precision Frequency Estimation Method for Echo Signal of Underwater Body Target

LIU Yanlong SHI Zhaoming

(Chongqing Bureau of the Navy Equipment, Chongqing 401100)

Aiming at that body target effect of target echo has an impact on the estimated Doppler frequency precision of echo signal in work area of torpedo acoustic-fuze, the Rife-Segmented Phase Difference Method is proposed. The high estimation precision of echo signal’s Doppler frequency is achieved by the method through combining the traditional Rife algorithm and the Segmented Phase Difference algorithm. It significantly improves the overall performance of the algorithm, fully retains the advantages of the two algorithms and overcomes the respective defects by the estimated signal frequency is preprocessed and different estimation algorithms are used in different frequency. Simulation result shows it can well extract Doppler frequency information of target echo in work area of the torpedo acoustic-fuze to achieve precise prediction of burst spot with high estimation precision and good stability, which has certain engineering application value.

underwater target, frequency estimation, Rife algorithm, segmented phase difference algorithm

2015年4月7日,

2015年5月26日

刘演龙,男,硕士,高级工程师,研究方向:水下信号与信息处理。石钊铭,男,硕士,工程师,研究方向:水下信号与信息处理。

TJ630.2

10.3969/j.issn.1672-9730.2015.10.039