声矢量阵双四元数模型及波束域DOA估计算法*
2015-03-15何光进游修东
何光进 游修东
(1.海军驻昆明地区军事代表办事处 昆明 650051)(2.91388部队 湛江 524022)
声矢量阵双四元数模型及波束域DOA估计算法*
何光进1游修东2
(1.海军驻昆明地区军事代表办事处 昆明 650051)(2.91388部队 湛江 524022)
针对传统的矢量水听器阵数据处理方法将水听器的输出用一复值的长矢量来表示,没有充分利用矢量水听器各振速通道的正交关系,提出了用双四元数对矢量水听器的输出数据建模,既保留了矢量水听器各通道间的正交性,又增强了对相关噪声的抑制能力。在此基础上,推导了波束域的双四元数方位估计算法,减少了算法的运算量,提高了算法在低信噪比下的分辨能力。通过仿真实验证明了算法的有效性。
水声; 声矢量阵; 双四元数; DOA; 波束域; MUSIC
Class Number TB566
1 引言
矢量水听器可以同时测量声场空间一点处的声压和质点振速的三个正交分量,且具有与频率无关的偶极子指向性,在对舰船辐射低频线谱检测与定位方面具有标量水听器无法比拟的优势[1]。利用矢量水听器对目标进行方位估计受到了广泛关注并产生了许多算法[2~7]。这些算法有以下的共同点:将单个矢量水听器的单快拍输出表示为一个列向量,将矢量水听器阵的输出沿阵列孔径方向排成一个更长的列向量。该方法的(本文称长矢量方法)实质是将单个矢量水听器看作为一个非空间共点阵列,各振速分量之间的正交性关系被舍弃,当单矢量水听器各通道的噪声相关时算法的性能急剧下降[8~11]。
2 声矢量阵双四元数模型
将单个矢量水听器的输出表示成
qc=p+ivx+jvy+kvz
(1)
其中,p、vx、vy、vz分别为矢量水听器的声压和三个振速通道的输出,且均为复数(虚部用I表示),i,j,k表示双四元数的三个虚部,且满足:i2=j2=k2=ijk=-1,ij=-ji=k,jk=-kj=i,ki=-ik=j。
式(1)中,将三路振速通道的输出放置于双四元数的三个虚部位置上,保留了笛卡尔坐标系中振速数据的正交特性。另外,上式通过一个双四元数完整地表达了单个矢量的输出,比传统的长矢量表达方式更加紧凑,在方位求解过程能够较大地节约内存空间和运算复杂度。
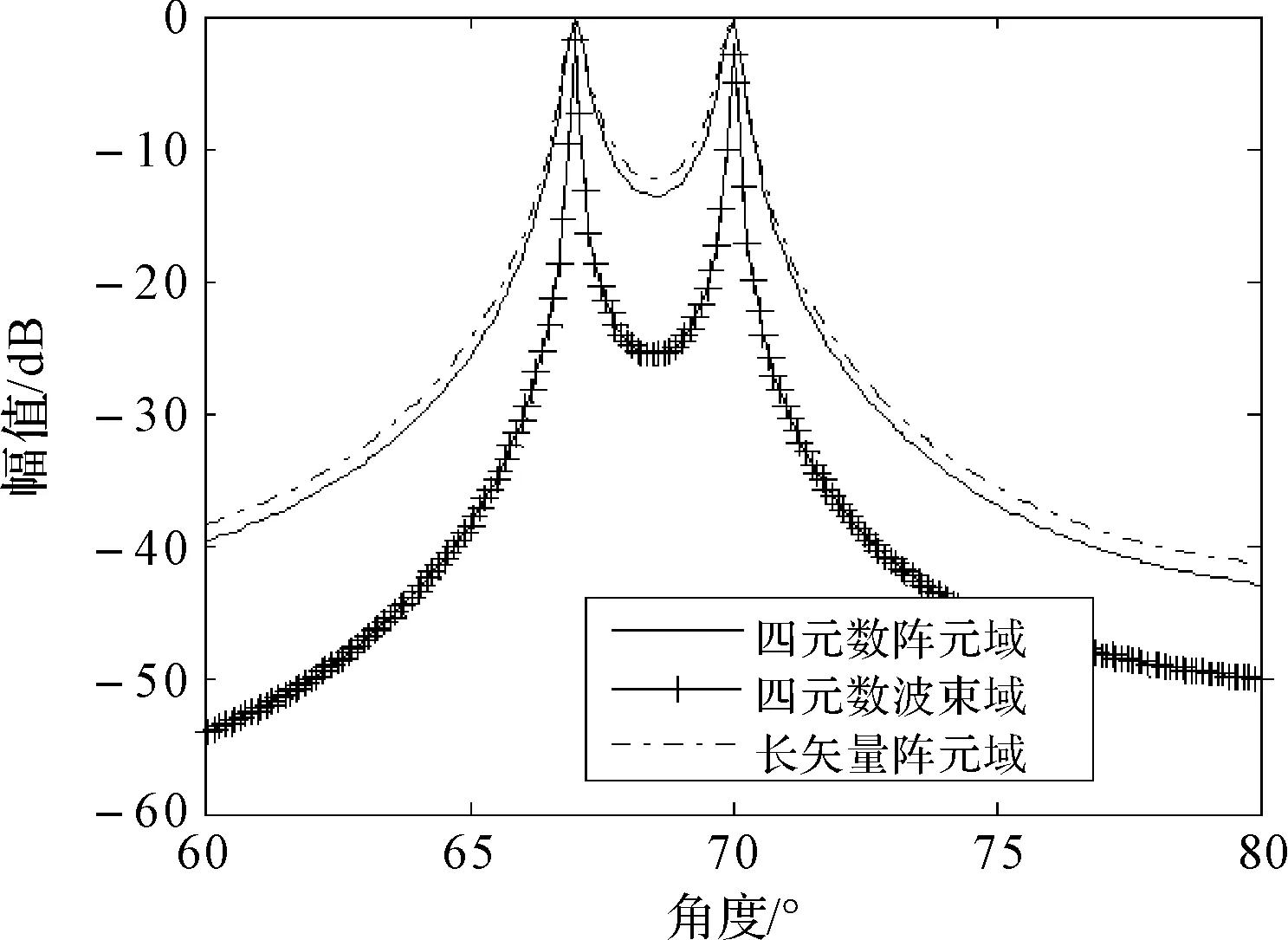
假设有M个配置相同的三维矢量水听器组成一均匀线阵,阵元间距为d。平面内有L个远场非相关窄带声源sl,l=1,2,…,L(L 结合液体介质中振速与声压的关系,矢量阵对第l个声源的响应可表示为 Zl= a(θl,φl)(1+icosθlcosφl+jsinθlcosφl+ksinφl)sl +nl (2) 其中a(θl,φl)=[1,e-j2πflτ1,…,e-j2πflτM-1]T为声矢量阵中声压子阵对声源sl的导向矢量,τl=dcosθlsinφl/c,c为声速。nl为满足高斯分布的噪声向量,其每个元素也为双四元数。 1)对预制光缆传输衰耗要求较高的工程应用,建议采用分支器型预制光缆;对施工效率及标准设计要求较高的工程应用,建议采用连接器型预制光缆。 则整个阵列对所有声源的响应为 (3) 其中,b(θl,φl)=a(θl,φl)(1+icosθlcosφl+jsinθlcosφl+ksinφl)为声矢量阵的双四元数导向矢量,n为噪声向量。 将上式写成矩阵的形式: Z=BS+n (4) 其中:B=[b(θ1,φ1),b(θ2,φ2),…,b(θL,φL)]为声矢量阵的导向矢量。 3.1 阵元域双四元数MUSIC算法 MUSIC算法利用观测数据协方差矩阵的噪声子空间和导向矢量的正交关系估计目标方位。首先计算式(4)的协方差矩阵: R=E{ZZH} (5) 其中“E{·}”表示取数据期望,“H”表示双四元数的共轭转置。需要说明的是,双四元数的共轭有多种不同的定义,本文指的是全共轭,即对双四元数的每一个四元数虚部(i,j,k)和复数虚部(I)均取共轭。 此时R为双四元数矩阵,在双四元数域内对其行奇异值分解,可得到噪声子空间,假设为Un(仍为双四元数)。根据MUSIC算法原理,得到如下的方位估计公式: (6) 与复数域的MUSIC算法相同,通过上式对θ和φ进行谱峰搜索,可得到目标的方位估计。 3.2 波束域双四元数MUSIC算法 波束域方位估计算法分为两步: 1) 通过多波束形成器将阵元域的观测数据转换到波束域; 2) 在波束域内运用方位估计算法进行DOA估计。 (7) 令变换矩阵为:w=TH,则w为D×M的双四元数变换矩阵。则矢量阵的输出可表示为 ZB=wZ=wBS+nB (8) 求式(8)的互协方差阵,得到噪声子空间UB,则波束域双四元数方位估计公式为 (9) 式(9)中所有的参数均为双四元数,在预成波束空间进行谱峰搜索,即可得到对目标方位的估计。 4.1 计算量分析 波束域算法的好处是可以减少计算量和提高算法的多目标分辨力。本节简要分析阵元域和波束域算法在计算量上的差别。对于阵元域算法,根据式(5),其协方差阵的维数为M×M,其特性分解的运算量为O(M3)。根据式(8)计算波束算法的协方差阵,其大小是D×D的矩阵,其特性分解的运算量为O(D3),由于D 4.2 仿真分析 1) 单目标估计精度 假设有一窄带声源以70°入射至12元声矢量线阵,用双四元数的阵元域、波束域和长矢量阵元域MUSIC算法对目标进行DOA估计方位估计结果如图1所示。从图中可以看出,在非目标方向上,双四元数波束域方法有更强的噪声抑制能力。 2) 双目标分辨能力 假设有两窄带非相干声源以方位角[67°,70°]入射至上述的声矢量阵。用本文提出的双四元数方法对两声源进行DOA估计,得到的方位谱如图2所示,仿真条件为:信噪比-10dB,快拍数为1000,背景噪声为高斯白噪声,各通道的相关系数为0.5。从图中可以看出,双四元数波束域方法有最好的目标分辨能力。 图2 双目标时的方位估计结果 根据双四元数的结构特点,将单个矢量水听器的输出数据用一双四元数表示,同时保留了各振速通道的正交性和数据的相位信息,与传统的长矢量模型相比具有明显的优越性。针对阵元域算法的缺点,将基于双四元数模型的声矢量阵MUSIC方位估计算法推广到了波束域,通过在波束域内对数据进行预处理,减少算法的运算复杂度并提高多目标分辨能力。分析仿真比较了波束域和阵元域MUSIC算法的运算量和方位估计能力,证明了双四元数模型在相关噪声背景下的优越性和波束域算法良好的分辨能力。 [1] 孙贵青,杨德森,时胜国.基于矢量水听器的声压和质点振速的空间相关系数[J].声学学报,2003,28(6):509-513. [2] 姚直象,胡金华,姚东明.基于多重信号分类法的一种声矢量阵方位估计算法[J].声学学报,2008,33(4):305-309. [3] B A Cray, A H Nuttall. Directivity factors for linear arrays of velocity sensors[J]. J Acoust. Soc. Am.,2001,110(1):324-331. [4] 张揽月,杨德森.矢量阵的非空间ESPRIT算法[J].哈尔滨工程大学学报,2009,30(4):406-410. [5] D Levin, S Gannot. Direction-of-arrival estimation using acoustic vector sensors in the presence of noise[C]//ICASSP,2011:105-108. [6] 梁国龙,张锴,付进,等.单矢量水听器的高分辨方位估计应用研究[J].兵工学报,2011,32(8):986-990. [7] 陈川,陈韶华,李琪.基于自适应Notch滤波器的矢量阵多目标分辨研究[J].兵工学报,2011,32(9):1131-1135. [8] M Hawkes, A Nehorai. Acoustic Vector-Sensor Correlations in Ambient Noise[J]. IEEE Journal of Oceanic Engineering,2001,26(3):337-347. [9] A Abdi, H Guo. A correlation model for vector sensor arrays in underwater communication systems[J]. OCEANS,2008:1-12. [10] 鄢锦,罗显志,侯朝焕.海洋环境噪声场中声压和质点振速的空间相干[J].声学学报,2006,31(4):310-315. [11] 邹吉武,孙大军,吕云飞,等.海洋矢量噪声场试验研究[J].哈尔滨工程大学学报,2011,32(1):16-20. Biquaternion Model of Vector Hydrophone Array and DOA Estimation in Beam Space HE Guangjin1YOU Xiudong2 (1. Navy Representative Office in Kunming, Kunming 650051)(2. No. 91388 Troops of PLA, Zhanjiang 524022) In the traditional vector data processing methods, the output of vector hydrophone array is expressed as a complex column vector, which cannot hold the orthogonality of the inside structure. Here, biquaternion algebra is employed to model the output of a vector hydrophone, which holds the orthogonality of the inside structure and is robust to coherent noises. What’s more, in order to cut down the computational complexity and improve resolution power, biquaternion based DOA algorithm of beam space is introduced. Simulations and comparisons are given at the end, which verify the efficiency of the algorithm. acoustic, vector hydrophone array, biquaternion, DOA, beam space, MUSIC 2015年4月7日, 2015年5月26日 何光进,男,博士研究生,工程师,研究方向:水下检测与识别、武器装备质量监督。游修东,男,硕士研究生,工程师,研究方向:水下目标特性,装备考核与试验方法。 TB566 10.3969/j.issn.1672-9730.2015.10.038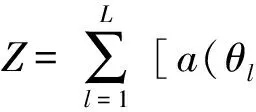
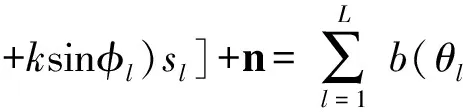
3 MUSIC方位估计算法
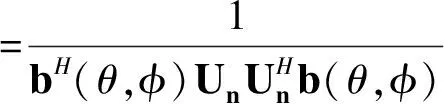
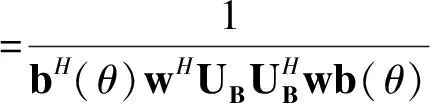
4 仿真分析
5 结语
