基于改进K-Means算法的雷电脉冲分类研究*

彭 丹 张曙霞

(海军工程大学电子工程学院 武汉 430033)



基于改进K-Means算法的雷电脉冲分类研究*

彭 丹 张曙霞

(海军工程大学电子工程学院 武汉 430033)

K-均值聚类算法因具有实现简单、快速有效、适合处理大数据集等优点而被广泛应用。但是由于初始聚类中心是随机选择的,K-均值聚类的结果对初始中心值具有很大的依赖性。另一方面,聚类的类数K也对聚类结果具有重要影响,一般情况下K是未知的,需要相关的专业知识对K进行预测,如果不能事先确定合适的K值,聚类的结果也会很不理想。本文提出一种改进的K-均值算法,避开了初始中心点的随机选择,只需计算数据集合中相距最远的两个点将其设为初始中心,同时不需要预先猜测聚类的数目,大大减小了用户的使用难度,聚类效果也显著提高。论文将改进的K-均值算法应用到自然雷电脉冲的分类中,并与传统K-均值算法的分类结果进行了比较。

K-均值聚类; 初始聚类中心; 聚类数目; 自然雷电脉冲

Class Number TP301.6

1 引言

甚低频通信是指利用频率为3kHz～30kHz的无线电波进行远距离信号传输的一种通信方式[1]。由于甚低频电波较高频电波而言在海水中的衰减较弱、能深入岩层,且具有传播较稳定、损耗较小的特点,因而甚低频通信具有重要的军事应用价值,甚低频对潜通信已成为海军远程指挥通信的主要手段之一。

甚低频通信的关键技术就在于甚低频接收机的设计。甚低频信道噪声主要成份是脉冲型大气噪声即雷电噪声,目前甚低频接收机性能测试都是在高斯噪声环境下进行,其性能指标只反映接收机在高斯噪声中的检测能力。由于甚低频信道的特殊性,接收机在真实环境中的性能指标与上述测量值相差很大,即接收机抗雷电干扰的能力无法评估。甚低频信道噪声模拟器产生以混合非高斯噪声模型为基础的大气噪声,可通过参数设定模拟不同气象环境和不同地域的实时噪声,构建接近真实的参数化甚低频信道测量环境,以有效地评估接收机在真实环境中的信号检测能力。另一方面,通过构建雷电噪声发生器,可以进一步研究改进接收机性能的抗雷电算法,可以大幅度地提高接收机的检测性能,减少漏报错报的概率。

构建雷电噪声发生器的一个重要环节就是对自然雷电脉冲的聚类研究。将收集到的自然雷电脉冲按特征进行分类,得到具有代表性的几类雷电脉冲的平均波形,将平均波形的值作为系数输入到成形滤波器。常用的聚类方法有基于划分、基于层次、基于密度、基于网格的聚类方法,基于划分的K均值聚类算法具有其他算法所不具有的高效性,并且实现简单,应用广泛。

2 K-均值算法及其研究现状

2.1 K-均值算法的基本思想

K-均值聚类算法由J. B. Mac Queen于1967年提出,用来处理数据聚类的问题,由于该算法实现简单,快速高效,适于处理大数据集,因此在科学研究和工业领域中都得到了广泛应用[2]。该算法解决的是将数据集合中的数据对象划分为K个类簇的问题。其基本思想是在数据集合中随机选取K个数据对象作为K个类簇的初始中心,计算各数据对象到各初始中心的距离,按距离最近原则,各数据对象被分到距离最近的那个中心所在的类簇中,形成初始的K个类簇;然后分别计算各类簇中数据对象的平均值作为各类簇新的中心,若新的中心与上一次的中心相比没有发生变化,则说明各数据对象已全部分配到自己所在的类簇中,聚类完成,否则继续重复上述过程,直到聚类中心不再发生变化。

K-均值聚类算法是一种典型的基于距离的聚类算法,采用距离作为相似性的评价指标,即认为两个对象的距离越近,其相似度就越大。该算法认为簇是由距离靠近的对象组成的,因此把得到紧凑且独立的簇作为最终目标。一般采用聚类误差平方和函数作为聚类准则函数,聚类误差平方和函数的定义为:

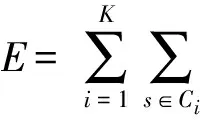
其中,K表示类簇的个数,s表示数据对象,Ci表示第i个类簇,mi为Ci的质心。E值越小,得到的聚类效果越好。

K-均值聚类算法的主要流程如下:

输入:数据对象集合S={s1,s2,…,sn}(每个数据对象具有r维特征),类簇的个数K。

输出:K个类簇Ci(i=1,2,…,K)。

1) 在数据对象集合S中随机选择K个数据对象作为K个初始簇的初始质心;

2) 计算S中各数据对象到Oi的距离

i=1,2,…,k,j=1,2,…,n

若满足

d(sj,Oi)=min(d(sj,Oi),i=1,2,…,k)

则sj∈Ni;

3) 各数据对象分配完成后,计算各类簇数据对象的平均值作为各类簇新的质心Qi(i=1,2,…,k);

4) 计算聚类误差平方和函数

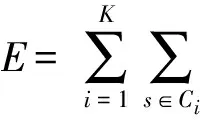
若E值收敛,则聚类完成;否则,返回步骤2)。

2.2 K-均值算法的不足

K-均值聚类算法虽然流程简易,快速有效,但仍然存在一些不足,主要存在以下两个方面的问题:

1) K-均值聚类算法中的类簇个数K需要用户预先给定,若K值选取的不合适,会使聚类结果很不理想。但是在实际应用中,一般很难预先确定K值的大小,需要相关的专业知识才能对K进行一定的预测,而预测的结果也不一定准确,这显然给用户的使用带来了很大的不便。

2) 由于K个初始中心的选择是随机的,K-均值聚类算法对初始中心点的选取具有很大的依赖性,不同的初始值会产生不同的聚类结果,导致聚类结果波动较大。另一方面,K-均值聚类算法作为聚类准则的误差平方和函数为非凸函数,非凸函数往往存在多个局部极小值,而全局极小值只有一个。误差平方和函数总是按着使其减小的方向进行搜索,不同的初始中心会使搜索沿着不同的路径进行,搜索到函数的值不再减小时算法就结束,得到的往往是局部最优,而非全局最优。

2.3 现有的对于K-均值算法的改进

K-均值聚类算法是数据挖掘技术中应用最为广泛的一种聚类算法。现有对K-均值聚类算法的改进主要从上面讨论的两个不足点入手,对于初始中心点的改进如下:

Shehroz等[3]提出了聚类中心初始化算法(CCIA)用来确定初始聚类中心。CCIA通过计算各数据对象属性的平均值和标准差来进行划分,然后将具有正态曲线的数据分到特定的类。实验测试证明,此算法与随机选取初始中心的传统K均值算法相比,聚类结果准确性更高,但其局限在于其中包含大量复杂的统计计算。

M.AlDauod[4]提出的算法是选取一系列具有最大方差的中间值,这些中间值从数据对象的某一维中提取。他们对不同的数据集合进行测试,此算法比其它算法产生更好的聚类结果。但是由于用到了中间值,此算法容易受离群点影响。

Kohei Arai等[5]利用分层算法来决定初始聚类中心的选取,聚类效果比K-均值算法有所提高。此算法适用于处理具有多维属性值的大数据集。此算法错分的概率比使用CCIA算法要高。

Mohammed El Agha等[6]利用ElAgha初始化算法,此算法根据数据的整体形状来确定初始聚类中心,能处理属性维度大的数据。

对于确定K值的改进如下:

Yiu-Ming Cheung[7]提出了一种新的聚类算法—步进式自动竞争—处罚K均值算法(STAR),该算法是传统K-均值算法的一种归纳,但又克服了以上讨论的传统算法的两个主要局限。此算法分两步完成,首先为每个类簇分配至少一个中心,然后按一个具有竞争—处罚机制的规则来进行调整。该算法的不足就在于复杂的计算。

V. Leela等[8]在K-均值算法的基础上提出了Y-均值算法。它首先对数据集执行K-均值算法,然后对类簇依次进行分离,删除,合并操作。此算法的缺陷在于需要先依赖K-均值算法进行聚类。

Mohamed Abubaker等[9]提出的一种新方法能同时解决初始中心点和K值的问题。此算法是基于最近邻法的原则,有两种版本,第一种需要同时输入最近邻数据对象的数目Kn和聚类数目K,数据点的分类列表将不断更新直到K到达指定的值,然后算法终止;另一种版本只需要输入最近邻数据对象的数目Kn,将同时得到聚类数目和分类列表。此算法的缺点是需要输入最近邻数据对象数目Kn。

B M Shafeeq等[10]提出的算法不需要事先确定K值而是在算法执行的过程中找到最佳K值。此算法的缺点是在处理大数据集时比传统K-均值算法花费更多的计算时间,同时用户在第一次执行时需要将K值设为2。

3 改进的K-均值算法

本文提出的改进算法不需要用户输入聚类数目K,此算法中,首先在数据集中选取相距最远的两个点作为初始聚类中心,数据集被分为两类,因为初始中心是相距最远的两点,所以这两类所包含的数据对象具有最大的不相似度。具体步骤如下:

输入:具有n个数据对象的数据集,数据对象具有m维属性A1,A2,…,Am

输出:n个数据对象被合理分配的适当个类簇

1) 计算每个数据对象所有属性值的和,为寻找数据集中相距最远的两个数据点做准备;

2) 选取属性值和最大和最小的两个数据点作为两个初始聚类中心;

3) 创建初始的两个类簇,通过计算各数据点到各初始聚类中心的距离将数据分配到距离最近的中心所在的类簇中;

4) 在两个初始类簇中寻找数据点到初始中心的最小距离,设其为d(d不等于0);

5) 分别计算步骤3)中两个初始类簇的数据平均值,将其分别设为两个类的新质心;

6) 计算各数据对象到新质心的距离,按以下准则找到离群点:若数据对象到质心的距离小于d,则此数据对象不是离群点;

7) 按6)中的准则找到离群点后,将离群点从两个类中删掉,形成两个新的类,重新计算两个类的平均值,得到新的质心;

8) 再分别计算7)中删掉的离群点到新的质心的距离,若满足6)中的准则,则将此离群点归入相应的类中,将剩余的离群点归为一类B,设B={Y1,Y2,…,YP};

9) (1)计算数据集B的平均值作为质心;

(2)按6)中的准则找到B中的离群点;

(3)如果离群点个数等于P,选取其中一个离群点作为一个新类C,计算其余离群点到C的距离,若距离小于d,则归入C中,形成新的类D,其余的依然为离群点;

(4)计算D的平均值得到新的质心,计算每个离群点到D的质心的距离,若符合6)中准则的则将其归入D中;

(5)此时B中剩余的离群点为B={Z1,Z2,…,Zq};

10) 重复9)中的步骤,直到B为空集。

4 实验测试与分析

为了测试算法的有效性,我们在Matlab中先随机地生成五个数据中心,然后围绕这五个数据中心生成随机的五组数据,五组数据组成一个大的数据集,如图1所示,然后分别用传统K-均值算法和改进后的K均值算法对其进行分类,分类结果分别如图2和图3所示。

图中的星号代表生成的五个数据中心,圆圈代表聚类后的五个质心,对比图2和图3可以明显地看出改进后的K-均值算法比传统K均值算法聚类效果好,而且改进K-均值算法不需要用户手动输入聚类数目K,减小了用户的使用难度。

图1 Matlab生成的数据集

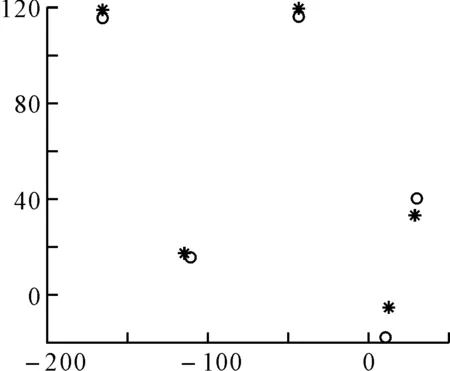
图2 传统K-均值算法的聚类结果

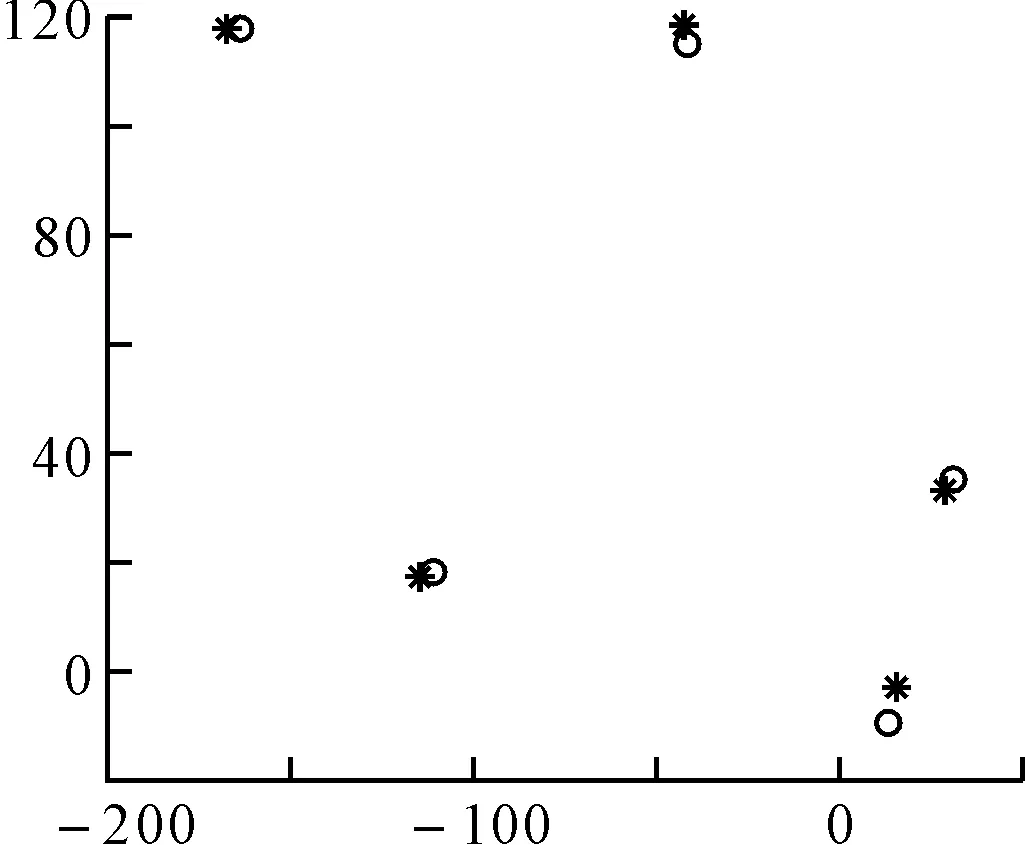
图3 改进K-均值算法的聚类结果

为了实现对自然雷电波形的分类并进一步验证改进K-均值聚类算法的准确性,分别用传统K-均值算法和改进后的K均值算法对自然雷电波形进行分类。由于自然雷电脉冲的幅值差别较大,若直接采用原始雷电脉冲进行分类,峰值大的雷电个体将占有极大的权重,在聚类过程中,这些雷电会很自然的聚在一起,而忽略了波形的相似程度,所以我们将原始雷电脉冲进行归一化后再进行聚类。我们总共采集到153个雷电脉冲,每个雷电脉冲大约持续800个样点,通过观察可以发现最具代表性的雷电冲击集中在第250到500个样点之间,所以提取出每个波形的第250～第500个样点作为实验数据,如图4所示,相当于用于聚类的数据集合中共有153个数据对象,每个数据对象的维数为251。

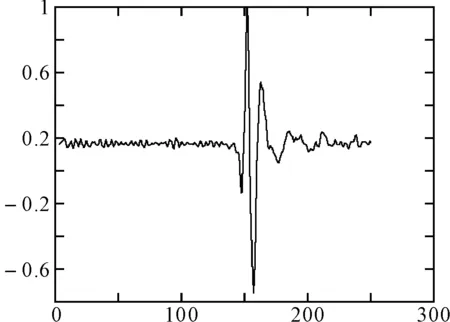
图4 归一化后的雷电脉冲

使用传统K-均值算法和改进后的K均值算法进行聚类后的结果分别如图5和图6所示。

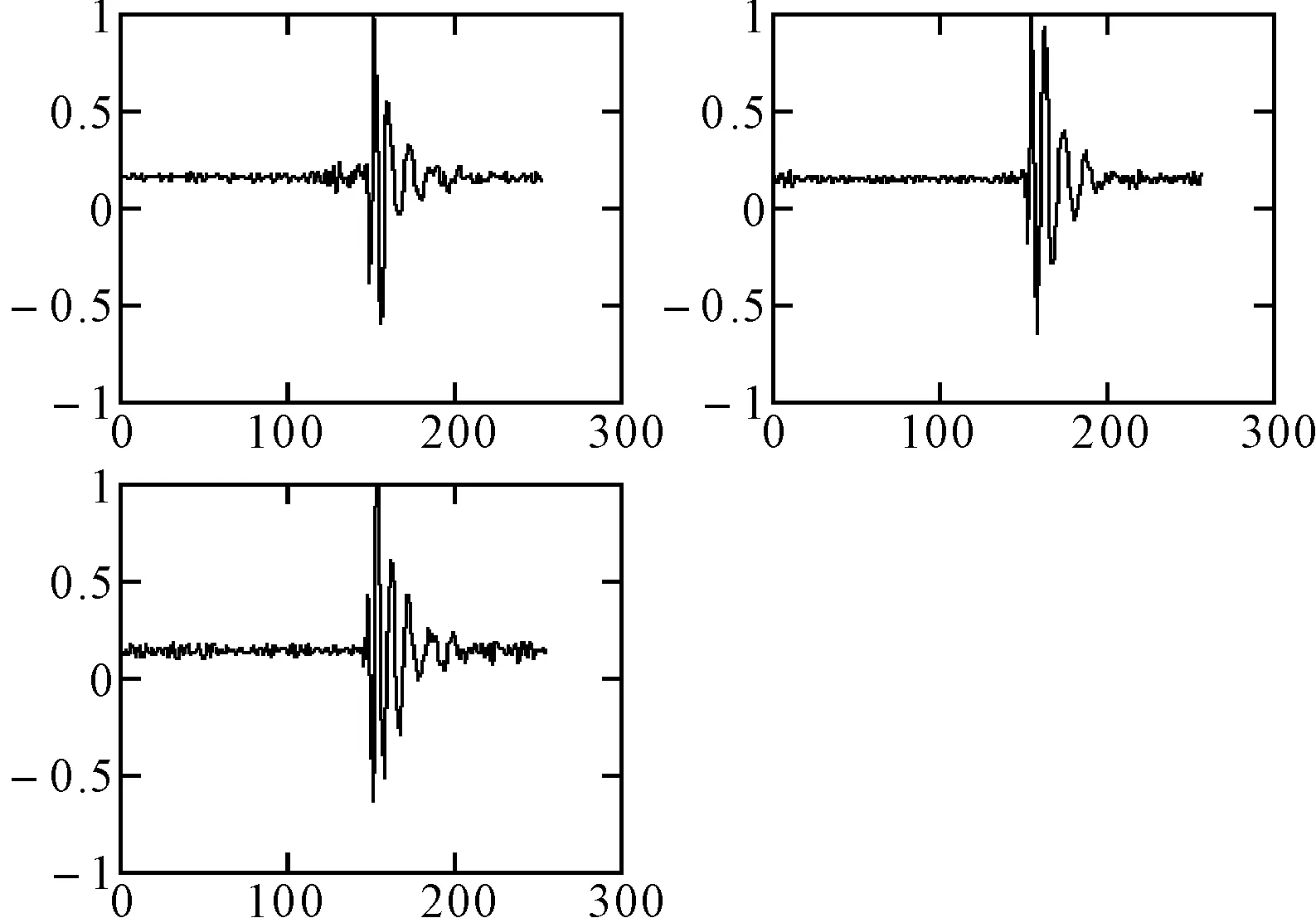
图5 传统K-均值算法的雷电脉冲聚类结果

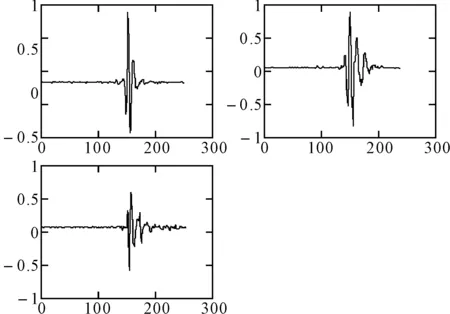
图6 改进K-均值算法的雷电脉冲聚类结果

每组的三个波形为聚类后每个类簇的平均波形,对比图5和图6可以看出,使用改进K-均值算法所得到的三个类簇差异性更大,聚类的本质就是要使相近的数据对象分到同一个类簇,而不同类簇中的数据对象保持高的差异度,所以改进后的K-均值算法得到的聚类结果更为合理。

5 结语

传统K-均值聚类算法易受初始中心点选择的影响而且需要手动输入聚类的个数K,给用户带来极大的不便,同时,若初始中心和K值选择不当,聚类效果会很差。本文提出的改进K-均值聚类算法避开了初始中心点的随机选择,只需计算数据集合中相距最远的两个点将其设为初始中心,同时也避开了K值的设定,聚类效果较传统K-均值聚类算法更为理想。本算法的局限在于只适合处理数值型数据,所以还需要继续研究,使其能对多种类型的数据进行聚类。

[1] 梁高权.甚低频波和超低频波的辐射与传播[M].武汉:海军工程大学出版社,2002:3-5.

[2] 王慧,申石磊.基于改进的K均值聚类彩色图像分割方法[J].电脑知识与技术,2010,6(4):962-964.

[3] Shehroz, Ahmad. Cluster center initiation algorithm for K-means clustering[J]. Pattern Recognition Letters 25,2004,2(1):1293-1302.

[4] M. AlDauod. A New Algorithm for Cluster Initialization[J]. World Academy of Science, Engineering and Technology,2007,4(1):102-107.

[5] Kohei Arai, Ali Ridho Barakha. Hierarchical K-means: An algorithm for centroids initialization for K-means[J]. Reports of the Faculty of Science and Engineering,2007,36(1):25-31.

[6] Mohammed El Agha, Wesam M. Ashour. Efficient and Fast Initializtion Algorithm for K-means Clustering[J]. I. J. Intelligent Systems and Applications,2012,4(1):21-31.

[7] Yiu-Ming Cheung. k*-Means: A new generalized kmeans clustering algorithm[J]. Pattern Recognition Letters 24,2003,3(2):2883-2893.

[8] V. Leela, K. Sakthipriya, R. Manikandan. A comparative analysisbetween k-mean and y-means Algorithms in Fisher’s Iris data sets[J]. International Journal of Engineering and Technology,2013,5(1):245-249.

[9] Mohamed Abubaker, Wesam Ashour. Efficient Data Clustering Algorithms: Improvements over K-means[J]. International Journal of Intelligent Systems and Applications,2013,5(3):37-49.

[10] B M AhamedShafeeq, K S Hareesha. DynamicClustering of Data with Modified K-Means Algorithm[J]. International Conference on Information and Computer Networks(ICICN 2012),2012,27:221-225.

Classification of Lightning Pulses Based on Improved K-Means Clustering Algorithm

PENG Dan ZHANG Shuxia

(College of Electronic Engineering, Naval University of Engineering, Wuhan 430033)

K-means has gained popularity because of its simplicity and rapid speed of classifying massive data rapidly and efficiently. However, the output of K-Means clustering algorithm highly depends upon the selection of initial cluster centers because the initial cluster centers are chosen randomly. The other limitation ofthe algorithm is to input the required number of clusters. This requires some sort of intuitive knowledge about appropriate value ofKwhich is sometimes difficult to predict as it requires domainknowledge. If the value ofKis not appropriate, the output of K-Means clustering algorithm will be bad. In this paper, we have proposed an algorithm based on the K-Means, but it avoids randomly choosing of the initial cluster centers, only setting the farthest two points in the data set as theinitial cluster centers. On the other hand, it does not require the number of clustersKas input. It greatly reduces the user’s difficulty and increases the quality of the result. This paper applys the improved K-means clustering algorithm to the classification of natural lightning pulses and makes a comparison with traditional K-means clustering algorithm.

K-means clustering, initial cluster centers, number of clusters, natural lightning pulses

2015年4月4日,

2015年5月27日

彭丹,女,硕士研究生,研究方向:通信理论与技术、甚低频信道探测技术。张曙霞,女,副教授,研究方向:通信技术。

TP301.6

10.3969/j.issn.1672-9730.2015.10.012