矩形管道内表面缺陷不规则面积检测模型研究与实现*

谢春思 李军玲 隋先辉

(1.海军大连舰艇学院导弹系 大连 116018)(2.大连大学信息工程学院 大连 116622)



矩形管道内表面缺陷不规则面积检测模型研究与实现*

谢春思1李军玲2隋先辉1

(1.海军大连舰艇学院导弹系 大连 116018)(2.大连大学信息工程学院 大连 116622)

针对光学镜头在检测小口径矩形管道内表面不规则缺损面积时,因探测镜头的空间自由度大,不能人为控制镜头探测拍摄时摄像镜头的位置和倾斜角度的难题,提出了一种矩形管道内表面不规则图像面积的图形梯形估算模型,通过实现应用表明,运用该估算模型进行不规则图形面积计算时,检测精度高,处理速度快,具有较好的工程应用价值。

矩形管道; 缺陷面积; 不规则; 估算模型

Class Number U455

1 引言

在图像检测对象中的图像处理、图像分析和图像理解可采用14个小类图像技术来分类[1],图像分析的最终目的就是根据检测手段与目标,通过合适的方法对原始图像中所表现的内容以最小存储空间、最快速度、易于计算的方法完成图像分析工作[2～3]。对于传统的不规则图像数据处理方法是以一定的分辩率获取检测对象的图像,在大背景小目标不规则成像机器视觉中文献[4]提出通过预注视机制减少图像处理的数据量,以达到提高检测精度与速度的目的;文献[5～6]提出采用可快速识别缺陷边缘的标记分水岭算法与多重分形频谱检测木材表面与内部缺陷的方法来检测;文献[7]提出采用三角形遍历法结合区域增长法来检测井下煤仓煤位不规则光斑图像的面积;文献[8]提出了不规则匹配加速算法。但对于小口径矩形管道内表面缺损不规则面积计算,由于检测获取图像的光学镜头角度、探测距离等无法确定因素的影响,缺损面积检测结果与实际情况相差较大,对于必须较好地提供检测诊断结论的图像分析结果难以达到实际要求。因此为了小口径矩形管道内表面缺损不规则面积的计算要求,提出了一种已应用于某了型雷达波导管检测仪的缺损不规则面积计算的图像处理梯形方法估算模型,得到的矩形管道内表面不规则缺损面积与实际面积高度吻合。

2 矩形管道内部损伤区域检测成像原理

作为雷达波导管是电磁信号传递的唯一途径,内表面的物理属性对信号传递有着极其重大的影响,其内表面具有特殊的高精度要求。由于其矩形口径小,弯曲多,表面光洁,而随着使用时间的增加常常导致内表面因各种原因造成一定程度的缺损而使信号出现不同程度的衰减。但是,常规检测设备根本无法深入其内部完成表面缺损的检测,如何检测其内表面的缺损具体情形而准确判断其工作性能始终是一个非常刺手的技术难题。经过长时间的探索与试验,终于从检测手段上与缺损不规则面积估算模型上得到了突破,较好地解决了小口径管道内表面缺损面积检测技术与计算问题,在实际应用上得到了满意的结果。

通过矩形管道内表面损伤区域面积估算的数学模型,在获取矩形管内损伤区域的图像后,为便于量化分析矩形管道内表面的损伤情况,需要估算损伤区域的面积。检测过程实际上是一个三维物体表面在计算机中的抽象的过程,理想的探测成像几何关系如图1所示。

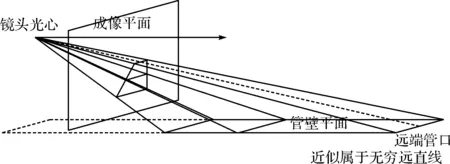
图1 理想的探测成像几何关系

为了能够从捕获的损伤图像中分析估算出损伤区域的面积,从而对整个矩形管段内壁的损伤情况进行评估,首先需要使用三维计算几何理论及相关模型,对摄像镜头进行标定,建立图像坐标与矩形波导管内壁的实物坐标之间的关联数据模型,然后,对图像中的损伤区域进行分析标记,再根据缺损面积估算模型计算出损伤面积。但由于摄像镜头深入波导管内部时,空间自由度很大,不能人为控制探测拍摄时摄像镜头的位置和倾斜角度,而且也不可能使用标准的标定参照物比对。因此,很难直接应用一般的摄像镜头标定模型。考虑到管内壁尺寸已知,又在很多情况下可以拍摄到远端的管口(即拍摄到的相对镜头的位于远处的矩形管口),为简化计算处理,模型中使用了人工设置远端管口辅助标记线(视为标定物)进行参照的方式。

3 损伤区域面积估算的数学模型

3.1 光学摄像镜头的标定

矩形管道内部检测的摄像镜头标定是指建立图像像素位置与场景点位置之间的关系。因为捕获的损伤图像中每个像素都是通过投射投影得到的,它对应于光学中心与场景点形成的一条射线。

在计算机视觉中,标定主要包括内参数和外参数两个部分。矩形管道内部检测标定的内参数:摄像镜头坐标系和理想坐标系之间的关系,给出摄像镜头光学和几何学特征[9]。包括主点、长宽比例因子和镜头畸变等。外参数表示摄像镜头在世界坐标系中的位置和方向,包括旋转和平移等。

在一定的摄像镜头模型下,基于标定物(人工标记的辅助参照线),经过对其进行图像处理,利用一系列数学变换和计算方法,求解得到摄像镜头模型的内部参数和外部参数模型参数如表1所示。

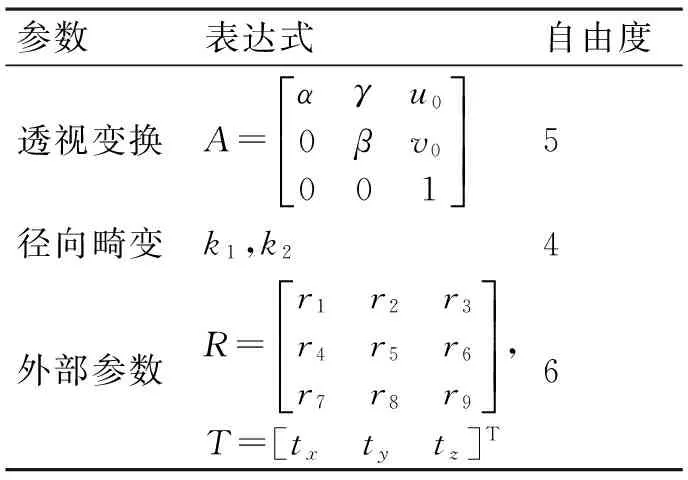
表1 摄像镜头的模型参数

表中,α,β,u0,v0,γ是线性模型的内部参数,其中,α,β分别是u轴和v轴的尺度因子,或者称为有效焦距,即α=f/dx,β=f/dy,这里,dx,dy分别是水平方向和垂直方向的像元间距,u0,v0是光学中心,γ是u轴和v轴的不垂直因子,这里令γ=0,即认为完全垂直。

R,T是外部参数的旋转矩阵和平移矩阵。对于非线性模型的内部参数,除了线性模型的内部参数α,β,u0,v0,γ外,还包括径向畸变参数k1,k2(切向畸变等忽略)。

3.2 光学摄像镜头模型坐标

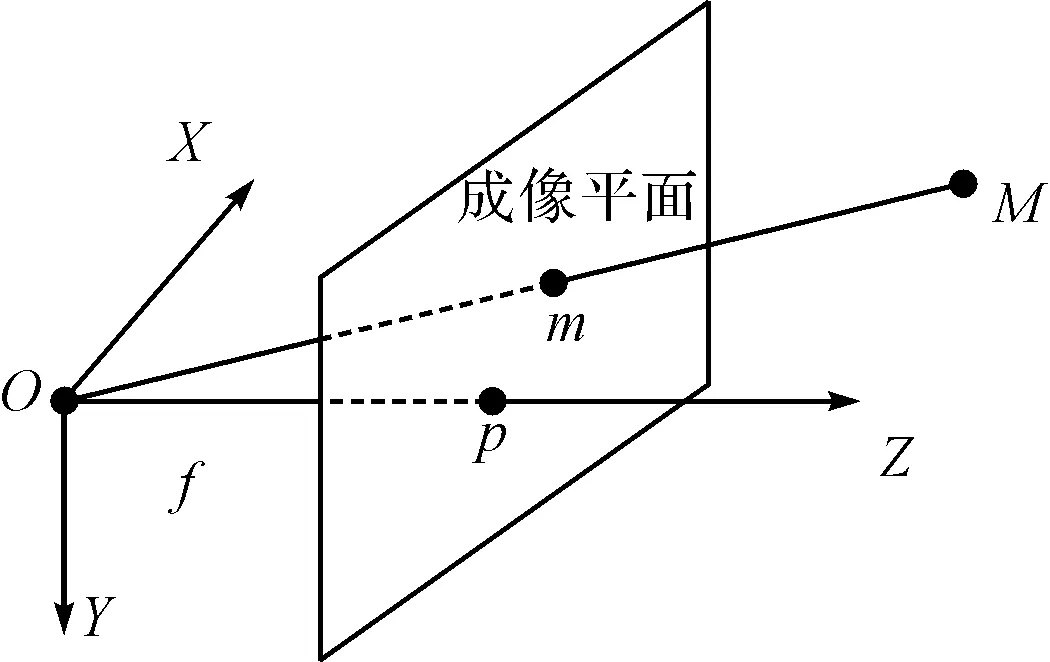
图2 小孔模型示意图

计算机视觉研究中,三维空间中的物体到像平面的投影关系即为成像模型,理想的投影成像模型是光学中的中心投影,也称为针孔(或小孔)模型,在这一模型中,主要由光心(投影中心)、成像面和光轴组成,严格依据小孔成像原理建立如图2所示,认为像点是物点和光心的连线与图像平面的交点。由于进行矩形管道内部检测镜头只有一个摄像镜头,因此,采用了单目摄像镜头模型。

为了定量表示光学成像过程,首先定义四个坐标系,然后建立出图像点与空间位置点的对应几何关系模型。这里,四个坐标系中的坐标轴均根据右手定则安排。

3.2.1 图像像素坐标系

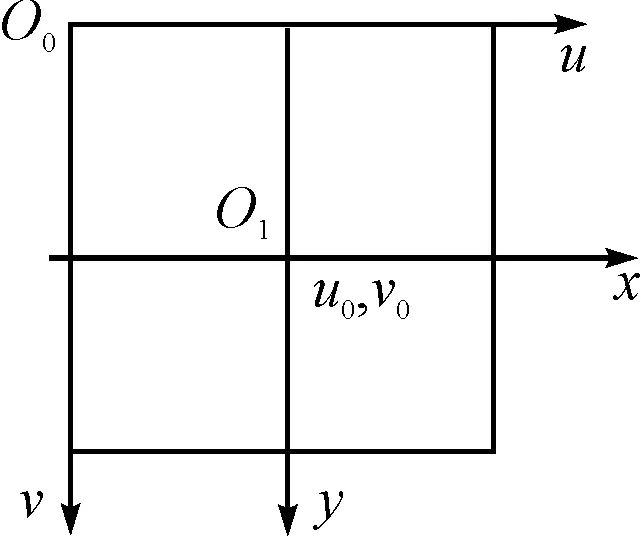
图3 图像像素坐标系和图像物理坐标系

摄像光学镜头采集的图像以标准电视信号的形式输入到计算机,经过数模转换转换为数字图像[10],每幅图像在计算机内可表示为M×N的数组,数组的每一个元素(像素)的值即是图像点的亮度值(或RGB三种颜色的亮度值),如图3所示,在图像上定义直角坐标系O2uv,原点O0在图像平面的左上角,每一像素的坐标(u,v)是以像素为单位的图像坐标系中的坐标,表示像素在数组中的行数和列数。

3.2.2 图像物理坐标系

为了能够用物理单位表示出某像素在图像中的位置,还需要建立以物理单位(如mm)表示的图像物理坐标系,如图3的O1xy,(x,y)以mm为单位表示像素在图像坐标系中的坐标。其中,O1原点称为图像主点,是摄像镜头光轴与图像平面的交点,在像素坐标系中的坐标为(u0,v0),通常位于图像中心处。x轴和y轴分别平行于u轴和v轴。两个坐标系之间的关系为式(1):

(1)

其中,dx和dy分别是x轴和y轴方向上单位像素之间的距离。

用齐次坐标与矩阵形式表示为式(2):

(2)

其中,γ是摄像镜头成像平面坐标轴并不互相正交引起的倾斜因子,这里忽略不计。

3.2.3 光学摄像镜头坐标系

如图4所示光学摄像镜头坐标系Oxcyczc是固定在摄像镜头的直角坐标系,其原点O定义在摄像镜头中心,xc轴和yc轴分别平行于图像物理坐标系的x轴和y轴,zc轴垂直于摄像镜头成像平面,与光轴重合。光心到成像平面的距离OO1为摄像镜头有效焦距f。

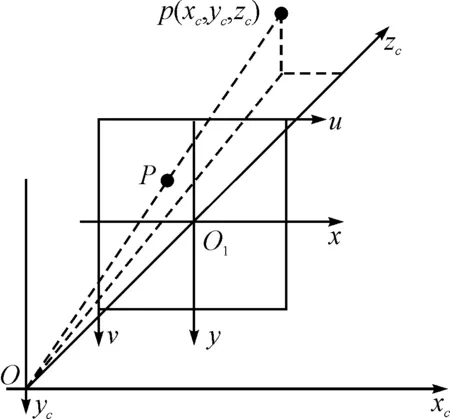
图4 摄像镜头坐标系和图像坐标系之间的关系

在光学摄像镜头坐标系和图像坐标系中,根据三角形相似原理,得到成像模型的代数表示如式(3):

(3)

3.2.4 世界坐标系(即实际物体坐标系)

由于光学摄像镜头与矩形管内壁的相对位置任意,还需要建立一个基准坐标系来确定摄像镜头的位置,以及矩形管内壁成像部分相对于摄像镜头的位置,即假想的世界坐标系Owxwywzw。世界坐标系中的坐标到光学摄像镜头坐标系中的坐标变换通过一个正交旋转矩阵R和一个平移变换矩阵T来表示如式(4):

[xcyczc]T=R[xwywzw]T+T

(4)

旋转矩阵R是光轴相对于世界坐标系坐标轴方向余弦组合,实际只有三个独立的角度变量(欧拉角):绕x轴旋转φ角(偏轴角),绕y轴旋转θ角(俯仰角),绕z轴旋转φ角(侧倾角)。此三个变量加上平移矩阵T的三个变量共六个参数,即为光学摄像镜头外部参数,得旋转矩阵R式(5):

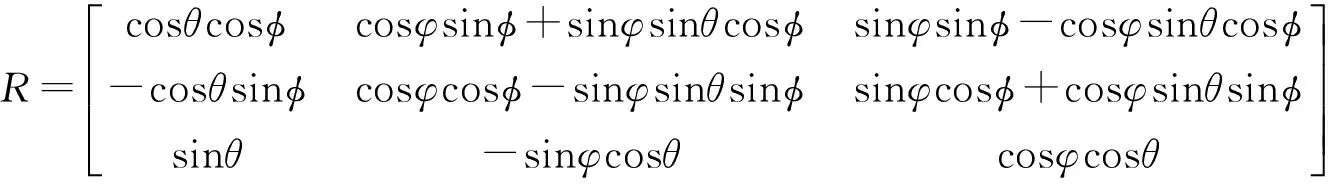
(5)

在此四个坐标系中,前二者为平面坐标系,是已知的,后二者为三维坐标系。若已知物体尺寸并以物体为基准选取世界坐标系,则世界坐标系也是已知的。

如图4所示,设(xw,yw,zw)是世界坐标系中某目标点P的三维坐标,(xc,yc,zc)是该点在摄像镜头坐标系中的三维坐标,在成像平面上的像点p的物理坐标和像素坐标分别为(x,y)和(u,v),则从世界坐标系到图像坐标系的变换过程如下:

1) 理想图像物理坐标系到图像像素坐标系的变换。

由式(2)可得齐次坐标和矩阵表示为式(6):

(6)

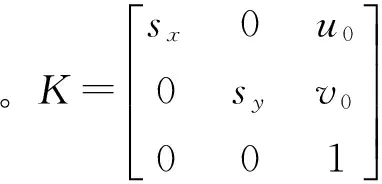
2) 光学摄像镜头坐标系到理想图像物理坐标系的变换。

单目光学模型下的理想透视投影变换后,可得式(7):

(7)

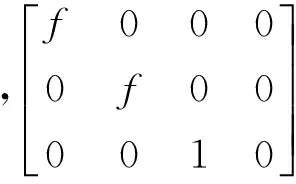
3) 世界坐标系和摄像镜头坐标系的刚性变换。

用齐次坐标和矩阵表示为式(8):

(8)

其中,0T表示(0 0 0)。

这里,世界坐标系与光学摄像镜头坐标系之间的变换由矩阵M2表示,只需要求出矩阵M2即可确定两者之间的转换。

由此,得到世界坐标系中的点P与其投影p的坐标对应关系为式(9):

(9)

其中,α=f·sx,β=f·sy;M1为内部参数矩阵;M2为外部参数矩阵;M为3×4的投影矩阵,表征了图像二维坐标与现实世界三维坐标的基本关系。

4 应用实例

如图5所示是某型雷达矩形管道内表面缺损检测分析结果。能够实现即时的快速检测与分析处理,缺损面积占比检测结果直观,在装备工程检测中得到了较好的检验。

图5 矩形管道内表面缺损检测分析结果界面

5 结语

当矩形管道内表面进行缺损面积检测估算时,采用常规不规则图像面积分析算法获取的估算值因不能确定探测镜头到检测物体表面的距离、摄像角度等必要条件而产生较大误差,实际工程应用价值不高。为了得到较可信的不规则缺损面积检测结果,采用图形梯形估算模型,经过工程应用与检验,矩形管道内表面不规则缺损面积估算精度高,分析处理快速,能够实现实时检测。

[1] 章毓晋.机器视觉和图像技术[J].自动化博览,2009(2):20-25.

[2] 王啟军,胡瑞敏,等.基于边界纹理一致性的帧内模板匹配预测算法[J].计算机工程,2012,38(3):227-229.

[3] 王振杰,盛焕烨.一种基于边缘梯度的图像分割方法[J].计算机应用研究,2004(2):254-257.

[4] 苏真伟,王瑾玮,等.不规则成像机器视觉系统探索[J].四川大学学报(工程科学版),2008,40(6):165-169.

[5] 陈永光,王国柱,等.木材表面缺陷边缘形态检测算法的研究[J].木材加工机械,2003(3):18-22.

[6] 韩书霞,戚大伟.多重分形理论在原木图像处理中的应用[J].东北林业大学学报,2011,39(10):132-133.

[7] 董玉杰,贾西科,等.井下煤仓煤位不规则光斑图像的检测方法研究[J].中国煤炭,2013,39(4):68-70,90.

[8] 钟凡,莫铭臻,等.基于WSSD的不规则图像块快速匹配[J].中国图像图形学报,2010,15(3):495-501.

[9] 李红俊,韩冀皖.数字图像处理技术及其应用[J].计算机测量与控制,2002,10(9):620-622.

[10] 孙杰,袁跃辉,等.数字图像处理自动图像聚焦算法的分析和比较[J].光学学报,2007,27(1):35-39.

Study and Realization of Irregular Defective Area on the Internal Surface of Rectangular Pipeline

XIE Chunsi1LI Junling2SUI Xianhui1

(1. Department of Missile, Dalian Naval Academy, Dalian 116018) (2. Information Technology Academy, Dalian University, Dalian 116622)

When optical scope detects the irregular defective area on the internal surface of small-bore rectangular pipeline, because of the high degree of spatial freedom of the detective scope, the position and angle of inclination of camera cannot be controlled artificially when detection. A trapezoid estimation model for the internal surface of rectangular pipeline irregular figure area is put forward. Through the practical application, it is shown that when applying the estimation calculation model to calculate the irregular figure area, the detective accuracy is high and the processing rate is fast, which has better engineering application value.

rectangular pipeline, defective area, irregular, estimation model

2014年10月20日,

2014年12月3日

国防重点课题(编号:2011ZW417)资助。

谢春思,男,博士,高级工程师,硕士生导师,研究方向:兵器科学与技术、装备维修工程。李军玲,女,硕士,副教授,研究方向:计算机技术应用。隋先辉,男,硕士,副教授,研究方向:导弹武器系统与计算机应用。

U455

10.3969/j.issn1672-9730.2015.04.041