导弹摆式机动与螺旋机动突防反导舰炮分析*
2015-03-15冯元伟
冯元伟 吴 强
(92941部队94分队 葫芦岛 125000)
导弹摆式机动与螺旋机动突防反导舰炮分析*
冯元伟 吴 强
(92941部队94分队 葫芦岛 125000)
为探讨摆式机动与螺旋机动对反导舰炮的突防能力,建立反舰导弹与反导舰炮对抗仿真模型,计算了多组机动周期、机动幅值、舰炮射速组合下,反舰导弹对反导舰炮的突防概率。结果表明,摆式机动与螺旋机动对反舰导弹突防能力均有大幅提升,且螺旋机动比摆式机动突防能力更强。而舰炮射速是决定反导舰炮反导能力的最关键因素。
舰炮; 机动; 仿真; 突防
Class Number TJ391
1 引言
众所周知,反舰导弹作为海面战场的主要进攻性武器,已成为现代海战主力。其作战效能将直接左右海面战场局面。但面对层层设防、不断完善的综合防御体系,其攻击能力仍大打折扣。为提高突防能力,反舰导弹近几年来的发展可谓突飞猛进、异彩纷呈,采用的技术也五花八门,令人刮目相看。但万变不离其宗,其突防策略始终离不开两个基本点:高速突防,机动突防。目前世界上大部分反舰导弹已具备高速巡航能力,且许多反舰导弹已装备有机动突防技术。如俄罗斯的“宝石”系列反舰导弹就规划有蛇形机动弹道,用以规避防空导弹的拦截。美国的鱼叉、意大利的奥托马特等反舰导弹则采用跃升俯冲机动来对付密集阵类近程反导舰炮武器系统[1]。虽然到目前为止,在反舰导弹与反导舰炮的攻防对抗中,除跃升俯冲机动模型外,尚未见到有其它机动方式付诸实施。但是不难想见,如果将蛇形机动、摆式机动和螺旋机动[2~4]等机动方式用于反舰导弹对反导舰炮的突防,肯定会有意想不到的效果。那么,当反舰导弹穿越多重屏障,面对最后一道防线—近程反导舰炮武器系统时,这些机动行为会为其增加几成胜算?为一探究竟,本文参考某亚音速反舰导弹与某反导舰炮武器系统之战术技术参数,建立二者攻防对抗仿真模型,系统研究了各种机动模式下,反舰导弹对反导舰炮的突防能力,得到了一些有价值的数据和结论[5~6]。本文着重分析比较摆式机动与螺旋机动对近程反导舰炮武器系统的突防性能。
2 仿真模型
仿真模型[7~8]包括各种理论值、测量值生成模型,反导舰炮火控解算模型、反导舰炮射击诸元理论值计算模型及脱靶量评估模型等,如图1所示。

图1 仿真计算流程
2.1 反舰导弹航迹模拟
2.1.1 坐标系
坐标系为左手直角坐标系,原点O在舰炮回转中心,X、Y轴在水平面内,X轴指向导弹主运动方向的反方向,Y轴指向X轴右侧,Z轴垂直向上。
2.1.2 摆式机动
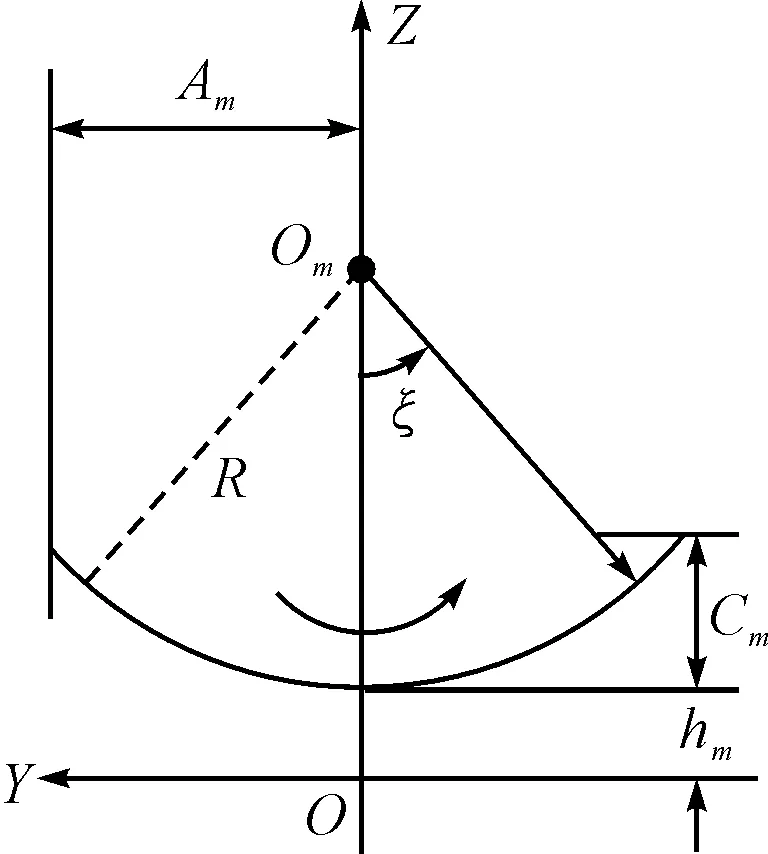
图2 摆式机动原理图
作摆式机动[9]的导弹,沿X轴反方向运动(速度为Vm)的同时,在YOZ面内像钟摆一样绕某点(Om)摆动。图2为其运动规迹于YOZ面内的投影。其中,Om是摆式运动的摆心(等同于钟摆的摆轴),R为摆长(等同于钟摆的摆臂长度),ξ为摆角(即摆心-导弹连线与铅垂线夹角的瞬时值),Am为摆幅(最大摆动幅度),Cm为摆深(导弹在一个机动周期内最大高度与最小高度之差),hm为导弹高度最小值。
由图2可知,导弹质心坐标(x,y,z)为
x=-Vm·t
y=Rsinξ
z=hm+R-Rcosξ
(1)
式中,t为导弹运动时间。摆角ξ与导弹X轴坐标x,x0有关,即
(2)
式中,ξmax是摆角最大值,l是节距,即导弹在一个机动周期内沿X轴飞行的距离,x0为起点坐标。
显然,导弹摆式机动轨迹与摆长R、最大摆角ξmax、节距l等有关,在仿真过程中调整这些参数,即能考察它们对舰炮命中概率的影响。图3是l=2800.0m、R=10.0m、Am=3.0m时,摆式机动轨迹的模拟图。
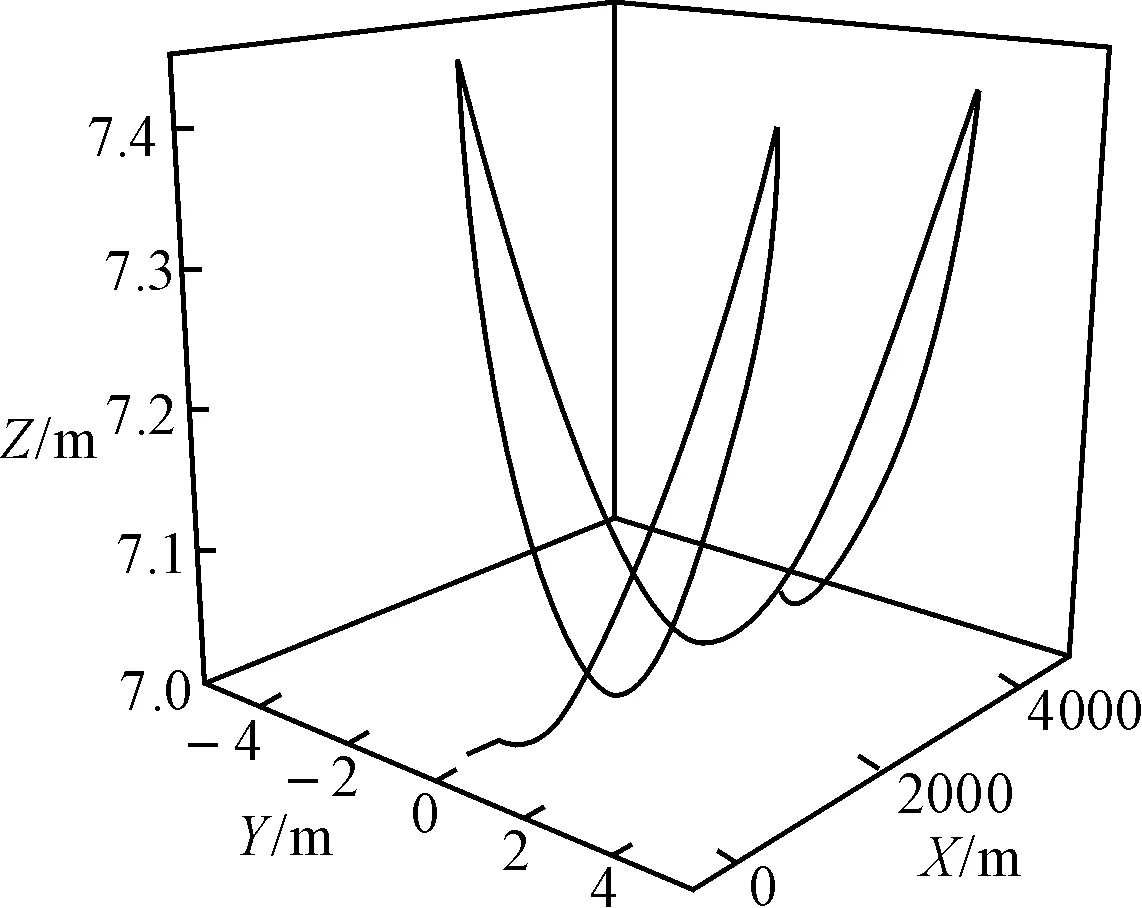
图3 模拟摆式机动航迹
2.1.3 螺旋机动
螺旋机动[9]也称滚筒机动。如图4所示,Xl是螺旋轴心线,导弹沿Xl轴运动(速度为Vm)的同时绕Xl轴作等速率圆周运动。图中l是螺距(导弹在一个机动周期内沿X轴飞行的距离),R是螺旋半径(导弹到直线Xl的距离),hm为螺旋轨迹最低点的高度,机动所需过载以n表示。显然,导弹螺旋机动轨迹与螺距、螺旋半径有关,在仿真过程中调整这些参数,即能考察它们对反舰导弹突防概率的影响。图5为某一螺旋机动轨迹模拟图(l=1400.0m、R=10.0m)。
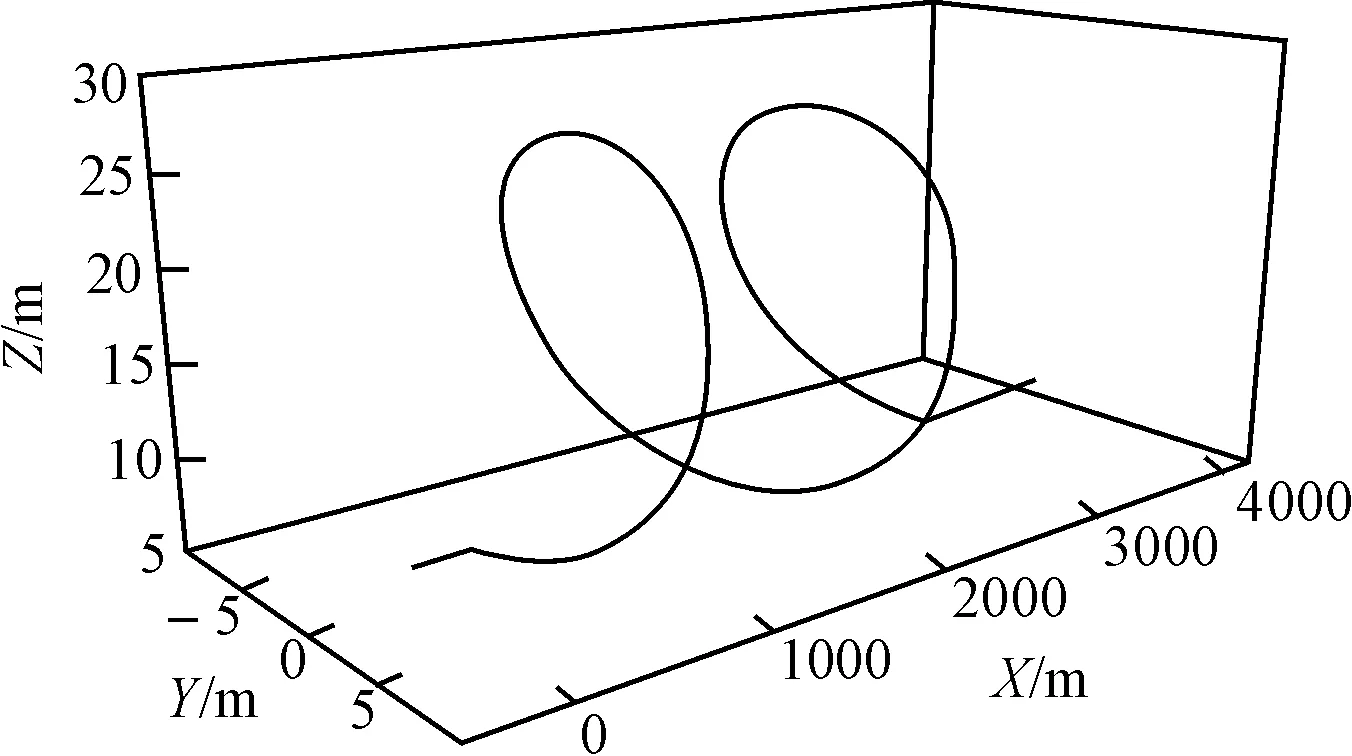
图5 模拟螺旋机动轨迹
2.1.4 导弹坐标探测模型
舰炮武器系统对导弹目标的跟踪探测设备为光电跟踪仪或跟踪雷达,一般情况下,其探测误差为平稳正态随机过程[10]。
2.2 舰艇运动姿态模拟
假设,舰炮所在舰艇理论上作等速直线运动。摇摆量、升沉量等姿态参数是具有一定周期、一定幅值的正弦量[11],且这些参数的测量误差服从正态分布。
2.3 气象参数模拟
弹道气象参数理论值,按均匀分布抽样产生。弹道气象参数包括弹丸初速、药温、气温、空气密度、风速风向等,其测量误差一般服从正态分布。其值在每个航次中抽样设置一次。弹道气象参数在求解舰炮射击诸元预测值(火控解算)与理论值时参与计算。
2.4 反导舰炮火控解算模型
假定舰炮武器系统火控解算采用卡尔曼滤波预测目标运动参数、未来点及射击诸元[12]。
火控解算所用数据,是各测量模型产生的测量值。
2.5 反导舰炮射击诸元理论值
反导舰炮射击诸元的理论值,用拉格朗日插值算法在导弹理论航路上求解[13]。参与计算的导弹坐标、舰艇运动参数(如航速、航向、摇摆、升沉等)、弹道气象参数等是各仿真模块生成的理论值。
2.6 炮弹脱靶量
反导舰炮射击总误差是火控解算误差(以Δγ、Δφ表示)、舰炮随动误差、炮弹散布误差三部分的合成。
考虑到随动误差与散布误差的不相关性,可先综合再抽样。记作γb、φb:
(3)
其中,v1、v2是正态分布随机数[14]。σγ0、σφ0与σγs、σφs分别是炮弹散布与舰炮随动误差在方位、高低两方向的均方差。
则航路上某射击点角脱靶量(F,E)为
方位:F=Δγ+γb
高低:E=Δφ+φb
角脱靶量与该射击点未来点斜距离的乘积,即是该发炮弹相对于导弹几何中心的线脱靶量,在X坐标系(Q平面)[15]内以(X1,X2)表示。
2.7 导弹被命中判断模型
根据反舰导弹几何特征及其与反导舰炮的相对位置、相对姿态等,求得反舰导弹的命中面积及圆形等效命中域半径r[15]。
将线脱靶量(X1,X2)换算为炮弹至导弹几何中心的最小距离rx:
(4)
那么,若rx≤r,反舰导弹被炮弹命中;反之未被命中。
2.8 突防概率
设n为仿真航次数,n1为导弹被命中的航次数,则突防概率P为
(5)
3 计算方法
计算方法步骤如下:
1) 参数赋值初始化。包括反舰导弹的几何参数;弹道气象参数的有效取值范围,舰艇运动特征量(摇摆周期、幅值等),各参数测量误差特征量(均值、均方差等),舰炮随动误差特征量,炮弹散布特征量,舰炮射击区段,以及仿真航次数等。
2) 设定机动方式(摆式机动或螺旋机动)、机动参数、舰炮射速等,循环仿真计算。
3) 每个航次开始前,集中进行一批随机抽样,以产生某些在一个航次中只需设置一次的参数值,如某些运动参数(导弹坐标、舰艇姿态等)的起始值,某些参数的系统误差以及气象参数等。然后开始一个航次的模拟。
4) 每个航次计算过程中,在舰炮的每个射击点,各理论值生成模块模拟产生相应参数(导弹坐标、舰艇运动姿态等)的理论值。这些理论值一方面参与计算射击诸元理论值;一方面经各测量模块模拟产生相应测量值,进一步驱动火控解算模块滤波求取射击诸元,并求该射击点的火控解算误差。
与此同时,舰炮射击误差生成模块模拟该发炮弹射击误差,经脱靶量计算模块计算出脱靶量,最后由命中判别模型判断该航次命中情况并予统计。
5) 算完所有航次,统计突防概率。
6) 调整机动方式、机动参数,或加倍舰炮射速,计算相应条件下的突防概率。
如此循环反复,直至计算完所有预设条件下的突防概率。
4 计算结果
4.1 摆式机动
1) 令摆深Cm=0.1m保持不变,节距l分别取350m、700m、1400m、2800m,计算突防概率随摆幅Am的变化情况,计算结果以图线表示(图6)。

图6 突防概率与摆式机动之摆幅之间的关系曲线
2) 令摆幅Am=3m保持不变,节距l分别取350m、700m、1400m、2800m,计算突防概率随摆深Cm的变化情况(结果见图7)。
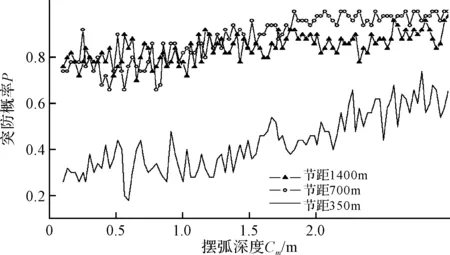
图7 突防概率与摆式机动之摆深之间的关系曲线
3) 令摆深Cm=0.1m,节距l=700m,将舰炮射速设为原来的2倍,计算突防概率随摆幅Am的变化情况,计算结果也在图6中表示。
4) 计算了摆式机动过载(如图8所示)。

图8 导弹摆式机动所需过载
4.2 螺旋机动
1) 计算了螺距l=700m、1400m、2800m时,突防概率随螺旋半径R的变化情况(如图9所示)。
2) 令螺距l=1400m,舰炮射速加倍,其它条件不变,计算突防概率随螺旋半径R的变化情况(结果一并示于图9)。
3) 计算了螺距l=700m时螺旋机动过载(见图9)。

图9 突防概率与螺旋机动之螺旋半径之间的关系曲线
5 结语
1) 无论摆式机动还是螺旋机动,均能大幅提升反舰导弹对反导舰炮的突防概率。机动周期(节距或螺距)越小,机动幅度(摆幅或螺旋半径)越大,突防概率越高。如图9所示,反舰导弹作螺距700m、螺旋半径2m的螺旋机动时,其对反导舰炮的突防概率可达90%以上。但无机动时的突防概率只有20%左右。
2) 由图5、图9可见,机动幅度较小时,随着机动幅度的增大,螺旋机动突防概率增加迅速,而摆式机动突防概率增加缓慢。因此,螺旋机动比摆式机动突防效果更好,所需过载更小,且机动幅度也小。这在机动周期较小时尤为明显。如节距和螺距同为700m时,欲达到80%的突防概率,螺旋机动所需过载不到1.2g,机动幅度(螺旋半径)也在2m以内(参加图9),而摆式机动所需过载却大于2g,机动幅度在3m左右(参加图6、图8)。进而也容易推知,以螺旋机动突防时,由于导弹机动幅度比舰艇轮廓小得多,所以,即使导弹在接近舰艇时始终保持机动,也不易丢失或错过舰艇。
3) 由图7可见,在摆式机动中,突防概率对摆弧深度很不敏感。而蛇形机动就是摆弧深度为0时的摆式机动,不难想象,摆式机动与蛇形机动的突防效果应该不相上下。
4) 可以看出,反舰导弹突防概率在很大程度上受制于舰炮射速。如导弹作螺距1400m、螺旋半径6m的螺旋机动时,舰炮射速提高1倍可使反舰导弹的突防概率降低1倍以上(参见图9)。因此舰炮射速是决定反导舰炮反导能力的最关键因素。
[1] 宋立,李勇,马良.反舰导弹对近程反导舰炮的机动突防模型分析[J].舰船电子工程,2009,29(9):122-124.
[2] 顾文锦,赵红超.超声速反舰导弹末端非平面机动研究[J].飞行力学,2003,21(3):36-40.
[3] 盖玉华,顾文锦,赵红超,等.反舰导弹的主要突防技术及其效能[J].海军航空工程学院学报,2008,23(2):168-170.
[4] 顾文锦,王凤莲.反舰导弹末端螺旋机动的控制研究[J].战术导弹控制技术,2003(2):2-7.
[5] 冯元伟,徐国亮,刘奎永.目标摆式机动对反导舰炮射击精度的影响[J].指挥控制与仿真,2010,32(2):101-103.
[6] 冯元伟,金振中,郜彪.导弹蛇形机动与摆式机动突防反导舰炮仿真[J].现代防御技术,2010,38(4):22-25.
[7] 邱志明.舰炮武器系统分析[M].北京:兵器工业出版社,1999:113-129.
[8] 程健庆.仿真建模技术在新型舰炮武器系统试验中的应用[J].计算机仿真,2002,19(1):54-58.
[9] 张翼飞,邓方林,顾文锦.反舰导弹末端机动弹道设计及弹道仿真[J].计算机仿真,2005,22(2):19-22.
[10] 杨文安,韩成标.基于白噪声的跟踪雷达量测误差建模与仿真[J].吉林大学学报,2005,23(6):621-627.
[11] 孙东彦,潘红华,徐明.某型舰炮火控系统建模与仿真[J].火力与指挥控制,2006,31(12):37-40.
[12] 王基组.舰炮火控系统原理[M].北京:海潮出版社,1999:83-193.
[13] 郑树敏,冯元伟,霍文志,等.GJB254A-2000舰炮武器系统设计定型试验规程[S].北京:国家军用标准,2000:39-42.
[14] 朱元昌.火控系统的数字仿真[M].北京:国防工业出版社,1992:39-48.
[15] 李小元,吴宇琼,周卫平,等.GJB 592.6-89,舰炮武器系统射击效力评定确定目标命中面积的方法[S].北京:国家军用标准,1988:1-5.
Analysis of Penetration of Cycloid Maneuver and Spiral Maneuver Missile Against Anti-missle Naval Gun
FENG Yuanwei WU Qiang
(Unit 94, No. 92941 Troops of PLA, Huludao 125000)
In order to discuss the penetration ability of cycloid maneuver and spiral maneuver against anti-missle naval gun, the combat engagement models of missile and gun were established,and the penetration probability in different conditions of two maneuver forms were computed respectively. The results show the penetration ability of anti-ship missile can be significantly increased by cycloid maneuver and spiral maneuver. Compared with the cycloid maneuver, spiral maneuver penetration ability is better. While the effective way to improve the anti-missile capability of the short range anti-missle naval gun weapon system is to increase its firing rate.
naval gun, maneuver, simulation, penetration
2014年10月3日,
2014年11月27日
冯元伟,男,高级工程师,研究方向:舰炮武器系统试验。吴强,男,工程师,研究方向:舰炮武器系统试验。
TJ391
10.3969/j.issn1672-9730.2015.04.031
