河工模型人工加糙的方法研究

宋为威 仲召伟 施晓欢

(扬州大学水利与能源动力工程学院，江苏扬州 225009)

河工模型人工加糙的方法研究

宋为威 仲召伟 施晓欢

(扬州大学水利与能源动力工程学院，江苏扬州 225009)

目前较多的河工模型试验都面临模型表面糙率较小的问题。本文介绍了在河工模型中提高表面糙率的方法，并对人工加糙糙率的计算方法进行了总结归纳，对满足阻力相似及提高模型的相似度具有重要意义。

河工模型;糙率;方法研究

在变态模型中，模型和原型之间需要满足阻力相似［1］。根据变态模型的阻力相似原则，一般需要人工增加糙率。目前，河工模型增加糙率的方法主要有:底面点块加糙;使用片状物(竹片、金属片等)立于河床上;底面条带加糙;金属丝网加糙［2］。在河工模型试验中常用的加糙方法是底面点块或竖向条杆;在浑水试验或者动床试验中常使用金属丝网加糙;在单纯研究水面线问题时，需要考虑流速分布和底面输沙的问题，常使用底面条带的加糙方法;在变态潮汐河工模型中，为模拟河道中涨落潮糙率的差异使用三角块梅花形加糙［3］。

1 人工糙率体的糙率系数和阻力系数的关系

模型河床上突出块体的迎水面积为a，小块体占河底面的面积为F，块体的体积为V，根据阻力可加性原理，在面积为F的河床上总切力是块体的阻力、块体的表面摩擦力和河床摩擦力之和，即

式中 Δ——块体在河床突出的高度;

Cd——块体的阻力系数;

h——水深;

if——床面摩擦比降;——块体表面摩擦比降;

γ——水体的重度;

ρ——水体密度;

is——水面比降，即单位水体对河床的总切力。进一步简化，可得

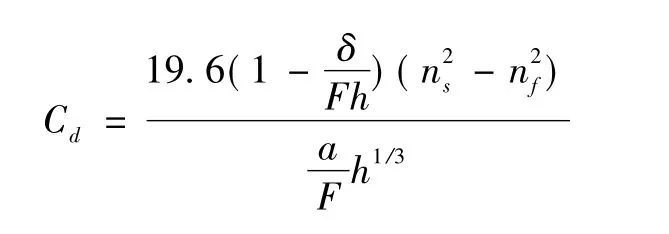
式中nf、ns——河床表面及加糙体后总的曼宁系数;

2 人工糙率的计算

不同形状块体在相同水流条件下对水的绕流试验所测得的阻力系数称为形状系数。据罗肇森河床阻力可加性原理［3］，得出人工加糙的河床糙率公式为

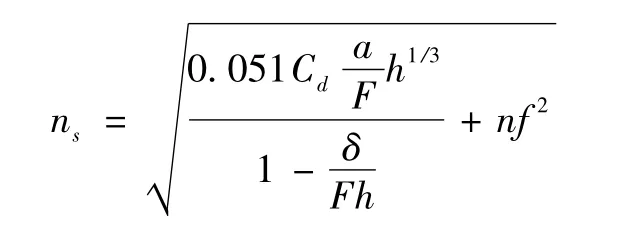
常见几种块体形状系数Cs见下表。

常见块体形状系数表

块体布置系数Cl按以下公式计算。

圆块或圆柱体

式中l——块体纵向距离;

d——块体直径;

b——块体的宽度。

竖向条杆加糙

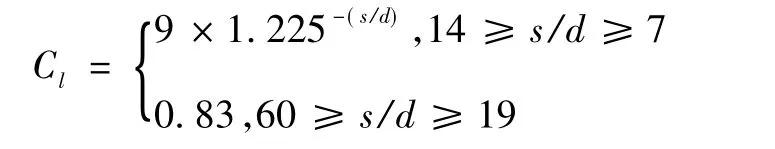
式中s——块体布置的斜距;

d——圆柱直径。

水深系数为

式中 Δ——河床突起的高度;

当河床间距排列时，取Δ=d;当颗粒密排时，取Δ=d/2;当颗粒稀疏排列时，取。

竖向条杆加糙

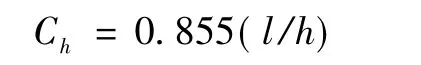
式中l——竖向条杆纵向的距离。

在计算梅花形加糙体糙率时，应考虑水深的计算基面，通常是扣除加糙体后被回流掩蔽水体折算厚度，计算水深的基面将会抬高。水深计算基面抬高，加糙随水深变化不大，适用于河道主槽加糙;水深计算基面直接取在床面，糙率随水深的增加而减小，适用于河道滩地及行洪区加糙。

不同水深计算基面糙率计算方法如下。

基面抬高情况

有效水深

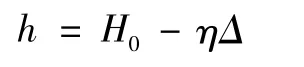
式中 λ——阻力系数;

Δ——十字板高度;b——十字板宽度;

L——相邻十字板距离;

H——以河底为计算基面的水深;

η——修正系数。

基面取河床面

具体计算时，根据模型比尺计算糙率nm及水深hm，再选择不同计算基面，计算模型的阻力系数λm。根据阻力系数及谢才公式

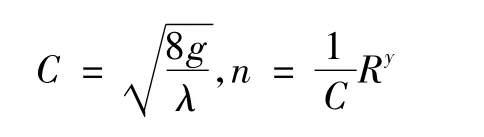
式中C——谢才系数;

R——水力半径;

在加糙体数量相同情况下，梅花形加糙的糙率值最大。底面点块加糙时，梅花形布置l/d数值比矩形布置得要大，且Cl随着l/d增大而增大。竖向条杆加糙时，梅花形的斜距与直径之比s/d的数值比矩形布置的大，且Cl随着s/d增大而减小。底面点块加糙的纵横距离比值l/p在0.83～1.11时布置，即以正方形或者接近正方形布置为限［3］。

3 新型人工加糙体研究

朱代臣等［2］对Y形加糙体水力阻力进行了研究，在河工模型水深变化范围较大，且糙体的体型较小时，具有一定相对尺度(h/Δ＞4，Δ是糙体的高度)。水深基准面的计算方法同样有两种:直接使用床面作为计算基准面和几何平均法。

在阻力平方区引用曼宁公式来计算糙率:

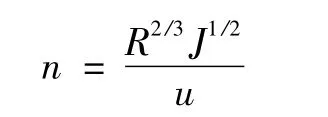
式中n——糙率系数;

J——水力坡度;R——水力半径;

u——断面平均流速。

考虑非宽浅明渠的水槽边壁对底板的糙率影响，使用郝登公式［4］计算Y型糙体的糙率:

式中nm——槽底糙率;

n1——槽壁糙率系数;n2——综合糙率;B——水槽宽;X——湿周;

h——有效深。

阻力系数使用糙率和阻力系数关系式计算，即f=

试验表明Y形加糙体的可调范围较大，为0.015～0.04。糙率为0.015上下时间距以20cm为宜;糙率为0.020上下时间距以15cm为宜;糙率大于0.028时间距以5cm为宜。相同淹没深度，Y形加糙体的水流阻力随间距加大而减小，且幅度渐小，最后稳定。在阻力平方区最小雷诺数低于3000;进入阻力平方区阻力随淹没深度的加大而减小，幅度逐渐变小，最后稳定。

为解决定床潮汐河工模型的加糙问题，陈志昌等［5］提出等腰三角形橡皮加糙的办法，三角橡皮块正反粘贴方向不同，其模型加糙的糙率也不同。徐华等［6］在类似块体计算公式或经验公式基础上，推导出三角块加糙体糙率公式及计算方法。

正向粘贴时，河床的总切力为块体绕流阻力、河床表面摩擦力及块体表面摩擦力的和，即

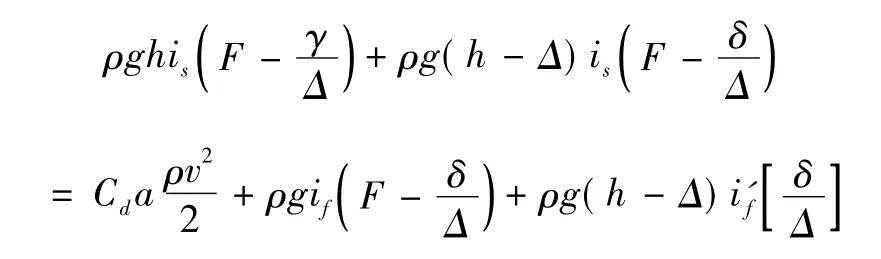
近似认为i'f=if，is和if的流速值相等，可得

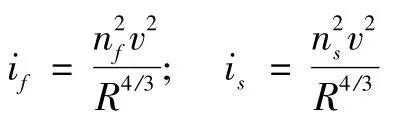
正向粘贴阻力系数Cd的表达公式通过徐华［1］等理论与使用归纳为

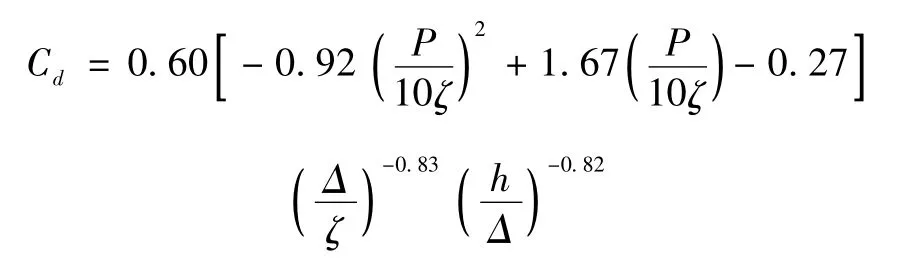
反向粘阻力系数的表达式与正向粘贴较为相似，同样通过文献［1］可得

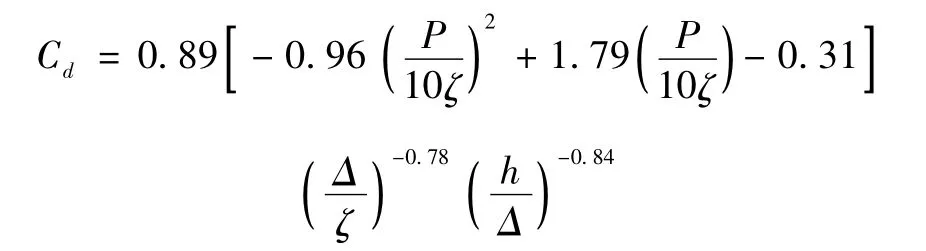
在确定了三角块的厚度、水深及布置方式后，根据上述正反向粘贴阻力系数代入下式可计算三角块正反向梅花形粘贴糙率:

试验表明:三角块正反向梅花形粘贴在宽水槽中通过均匀流的试验研究，运用谢才公式计算两种加糙方式的糙率。据阻力开加性推导糙率计算公式，实测与偏差在10%之内［6］。

张瑾［7］在进行淮河入江水道(上段)金湖段的植被对河道水力特性影响研究时，通过对有芦苇的河道进行阻力分析，推导出如下糙率公式:

植被没有被淹没情况下综合糙率公式为

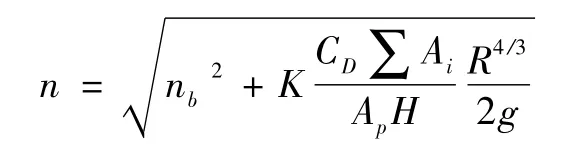
植被被淹没情况下综合糙率公式为

试验表明:在无芦苇情况、苇草现状及全苇草情况下，糙率随流量的加大而加大;在同一流量情况下，糙率随苇草的增大而增大，即苇草密度增大导致糙率的增大。

4 结语

河工模型人工增加糙率从传统的底面点块、片状物、底面条带及金属丝网发展到新型人工加糙体的研究，在这一过程中反复论证了传统方法的优越性，并使糙率计算公式得到完善和验证。传统的糙率计算方法将会继续催生更多的新型人工加糙体，并且一直是新型人工加糙研究的源头。

［1］徐华.潮汐河工模型三角块梅花形加糙试验研究及其应用［D］.南京:南京水利科学研究院河港研究所，2006:15-23.

［2］朱代臣.长江防洪实体模型阻力特性研究［D］.武汉:长江科学院，2008:10-13.

［3］罗肇森，孙梅秀.河工模型中几种人工糙率的计算［J］.水利水运科学研究，1981(2):70-82.

［4］左东启.模型试验的理论与方法［M］.北京:水利电力出版社，1984.

［5］陈志昌，黄仁元，胡志峰.长江口潮汐模型设计和验证［J］.水运工程，1992(10):60-66.

［6］徐华.潮汐河工模型三角块梅花形加糙试验研究及其应用［J］.水利水运工程学报，2007(4):54-61.

［7］张瑾.植被对河道水力特性影响的研究［D］.扬州:扬州大学，2011:86-87.

［8］钱宁，万兆蕙.泥沙运动力学［M］.北京:科学出版社，1983.

Study of Artificial Roughening Method of Movable-bed Model

SONG Weiwei，ZHONG Zhaowei，SHI Xiaohuan
(Yangzhou University Water Resources and Energy Power Engineering College，Yangzhou225009，China)

More movable-bed model tests suffer from problem of low model surface roughness currently.In the paper，method of improving surface roughness in movable-bed model is introduced.Calculation method of manually increasing roughness is summarized and concluded.It has important significance on meeting resistance similarity and improving similarity of model.

movable-bed model;roughness;method stndy

TV83

:A

:2096-0131(2015)01-0069-04