基于数学模型研究三亚市区绿地生态破坏后盖度恢复

王湘君,陈 文,杜 宇,黎 明,符家磊,王胜楠

(琼州学院 a.热带生态与环境保护学院;b.两栖爬行动物研究省级重点实验室; c.食品学院; d.热带生物与农学院;e.数学系, 海南 三亚 572022)



基于数学模型研究三亚市区绿地生态破坏后盖度恢复

王湘君a,b,陈 文c,杜 宇b,d,黎 明d,符家磊e,王胜楠a

(琼州学院 a.热带生态与环境保护学院;b.两栖爬行动物研究省级重点实验室; c.食品学院; d.热带生物与农学院;e.数学系, 海南 三亚 572022)

用生态数学模型方法研究三亚市区绿地生态破坏后物种在自然状态下盖度恢复的程度、速度和难度.在某高校A的四块区域选择12个天然草地样方,人为破坏样方内的全部表层植被,并使其自然恢复.结果表明:15周以后,实验区域的物种盖度基本恢复到破坏前水平;Logistic拟合曲线作为植物盖度恢复的生态数学模型,拟合度均为0.999左右.

绿地生态;自然恢复;盖度;数学模型

0 引言

生态学在自然科学中是一门年轻的学科,也是最有活力的学科之一[1].城市绿地生态系统,复合生态系统中的子系统,具有生产能力和自我调节能力[2].数学模型常用于生态系统的研究过程中,可以通过综合分析环境信息,定量刻划生态系统功能(如完整性、稳定性、灵敏度、多样性等)[3].本研究选取海南岛南部城市三亚,某所高校内四块天然绿地,建立盖度恢复数学模型.

1 材料与方法

实验时间与地点:2014年10月1日至2015年1月31日,在某高校A移动与电信营业厅、体育馆足球场、学生宿舍公寓楼、行政大楼旁边的天然草地,每个区域随机选取3块1m2作实验标准样方,每周测量一次参数变化.

实验方法:测出各样方的盖度等指数后,将样方内全部草本植物和矮灌木地面茎叶和浅层地下根铲除,再使其自然恢复.盖度测量采取拍照后,用CAD软件辅助计算.

2 结果与分析

12个标准样方破坏前的植物盖度信息统计如下表1样方破坏前,盖度较高的植物有牛筋草、牵牛花、鸭跖草等.

表1 样方破坏前的原初盖度及植物种类

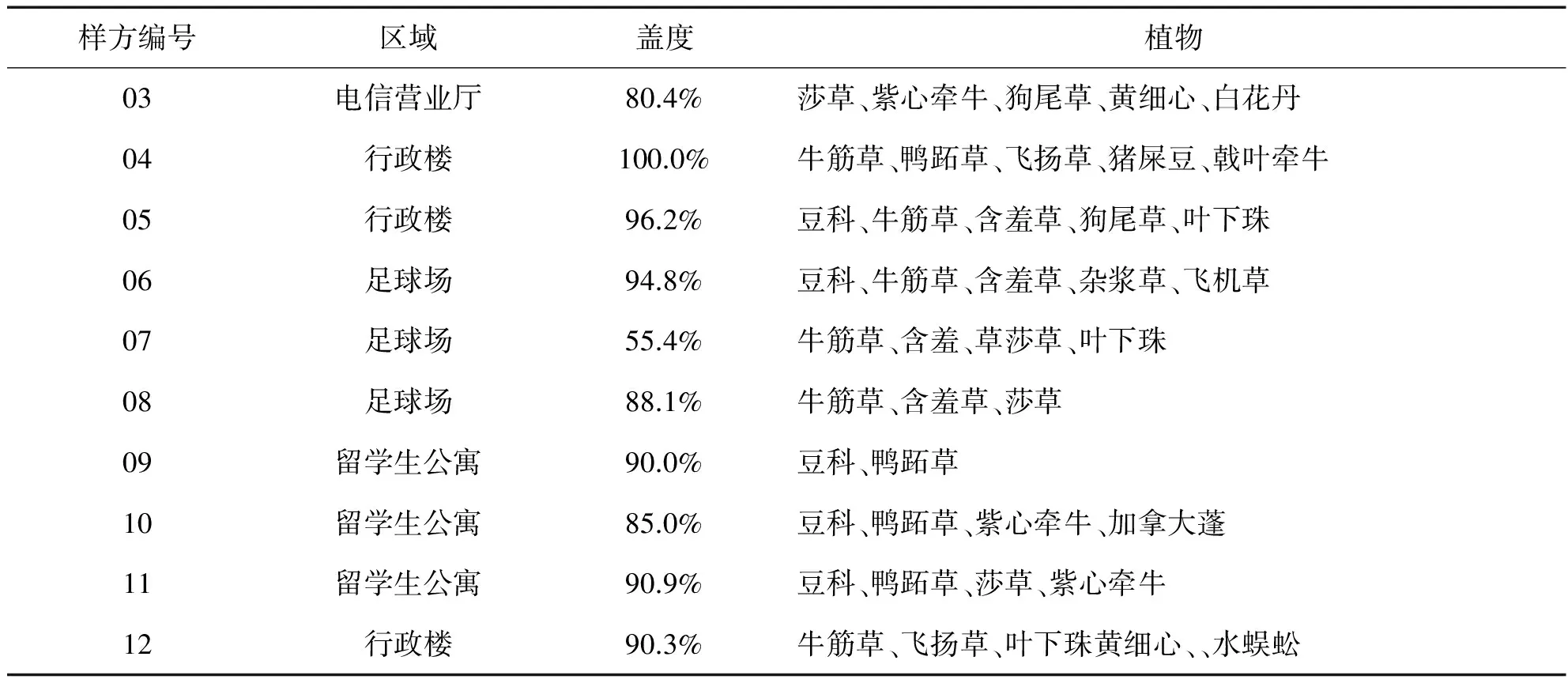
续表1

4个区域,12个标准样方破坏后,连续16周记录盖度恢复信息,统计如表2.

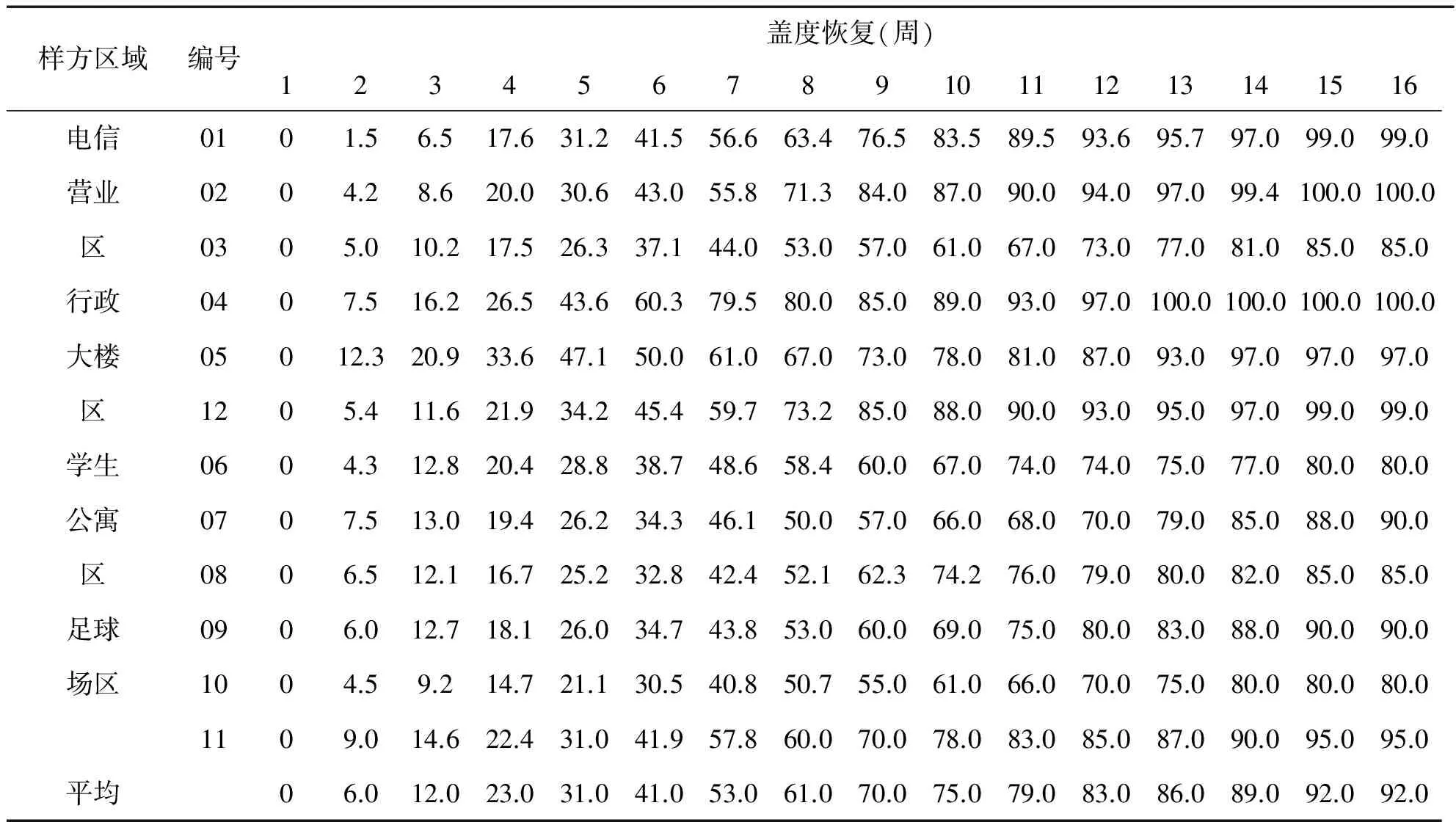
表2 实验样方盖度恢复(%)

盖度按照所选的四个区域来分析,以恢复周数为X轴,取每个区域内的三个样方每周盖度的平均数为Y轴,绘制散点图,添加拟合曲线.

2.1电信营业厅区样方恢复

运用Origin7.5软件,采用线性拟合、指数拟合、对数拟合、多项式拟合、乘幂拟合、Logistic曲线拟合等方法,建立数学模型,见表3.

表3 电信营业厅区样方盖度恢复拟合数学模型

续表3

图1 电信营业厅区盖度恢复的Logistic拟合曲线

由表3可知,Logistic曲线的拟合度超过0.999,故选择此作为拟合曲线.由图1得知,电信营业厅绿地的盖度在4-8周期间恢复速率较快;第6周为拐点周,对应盖度为40.5%,此时的恢复度为42.3%;9周以后恢复速率减慢,15周以后基本饱和.而此区域的初始平均盖度为91.7%,盖度恢复到破坏前的104.6%.

2.2 行政大楼区样方恢复

同理,运用Origin7.5软件,采用线性拟合、Logistic曲线等方法进行拟合,建立6种数学模型,见表4.

表4 行政大楼区样方盖度恢复拟合数学模型

图2 行政大楼区盖度恢复的Logistic拟合曲线

由表4可知,Logistic曲线的拟合度最接近0.999,故选择此作为拟合曲线.由图2可知, 行政大楼区草坪盖度在5-7周期间恢复速率较快;其拐点周为第6周,对应盖度为51.9%,此时的恢复度为54.7%;9周以后恢复速率减慢,14周以后基本饱和.而此区域的初始平均盖度为95.3%,盖度恢复到破坏前的103.7%.

2.3 学生公寓区样方恢复

同理,运用Origin7.5软件,建立6种数学模型,见表5.

表5 学生公寓区样方盖度恢复拟合数学模型

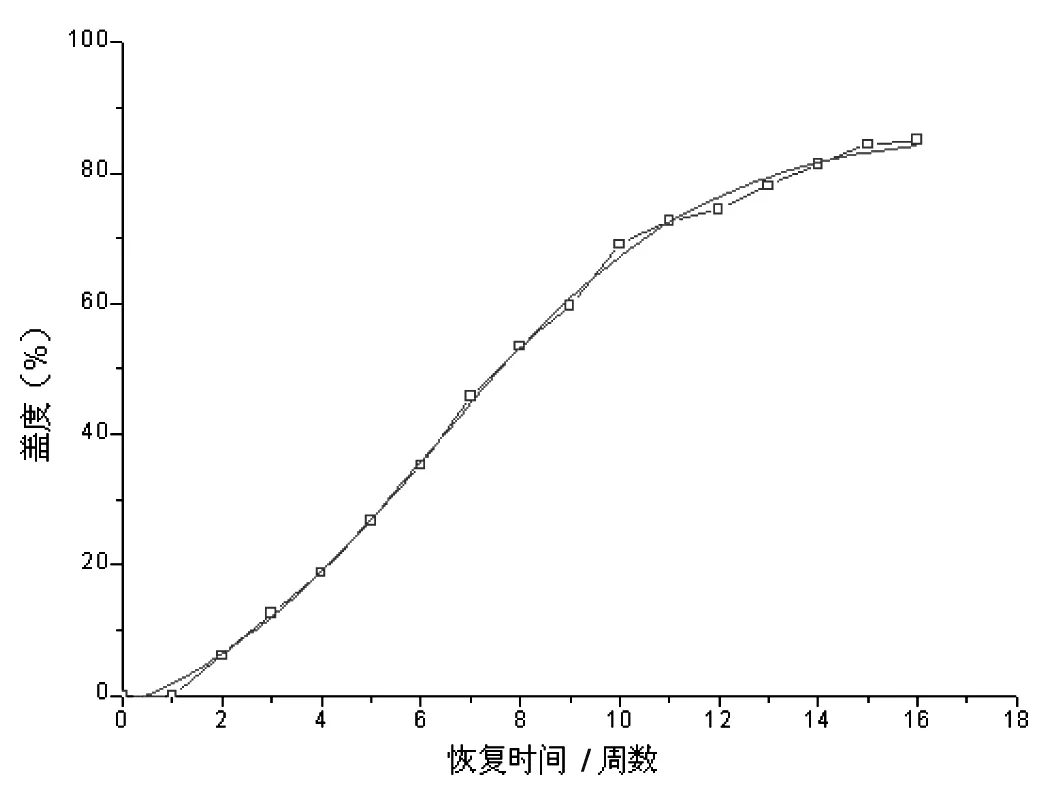
图3 学生公寓区盖度恢复的Logistic拟合曲线

由表5可知,Logistic曲线的拟合度最接近0.999,故选择此作为拟合曲线.由图3可知,学生公寓区草坪盖度在4-8周期间恢复速率较快;其拐点周为第6周,对应盖度为36.8%,此时的恢复度为42.3%;9周以后恢复速率减慢,15周以后基本饱和.而此区域的初始平均盖度为88. 7%,盖度恢复到破坏前的101.4%.

2.4 足球场区样方恢复

同理,运用Origin软件,建立数学模型,见表6.

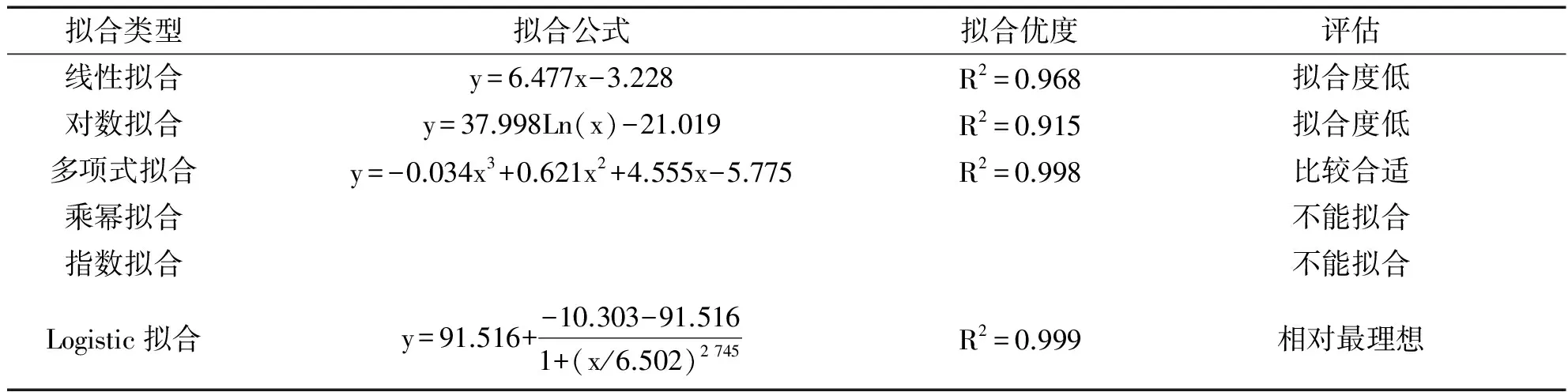
表6 足球场区样方恢复拟合数学模型

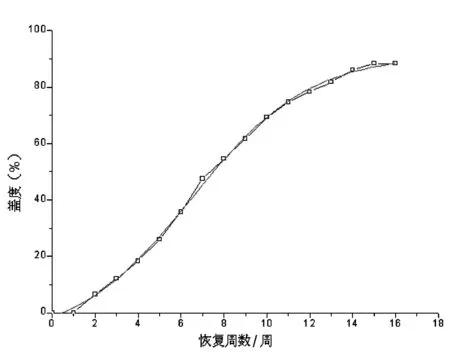
图4 足球场区盖度恢复的Logistic拟合曲线

由表6可知,Logistic曲线的拟合度高于0.999,因此作为数模拟合曲线.由图4可知,足球场区草坪盖度在4-7周期间恢复速率较快;其拐点周为第6周,对应盖度为37.2%,此时的恢复度为40.7%;10周以后恢复速率减慢,15周以后基本饱和.而此区域的初始平均盖度为79.3%,盖度恢复到破坏前的115.4 %.

3讨论

通过建立某高校A四块区域天然草坪盖度恢复的数模可以得出:对于乘幂拟合和指数拟合,都不适合;线性拟合和对数拟合的拟合度不算高,仅0.990;三项式拟合的拟合度较高,约0.995;Logistic曲线拟合的拟合度最高,约0.999.

四个区域的盖度恢复过程非常相似,快速恢复期都在5-7周,Logistic曲线拐点都在第6周,此时对应的盖度为40%左右,恢复度为40-50%,平均45.0%.10周以后,恢复速度明显减慢,此时对应的盖度为75%左右,恢复度为78-90%,平均84.0%.15周以后基本饱和,此时对应的盖度为92%左右,恢复度为101-106%,平均106.3%.

结合此前进行的丰度恢复分析可以看出[4],丰度的快速恢复期主要在2-5周,拐点在第3周,而盖度恢复的拐点在第6周;大约7周后,丰度恢复趋于平稳,而盖度恢复须15周.丰度恢复明显快于盖度恢复,符合岛屿物种侵入理论[5].盖度略高于被破坏前,符合中度干扰理论[5].

4 结论

三亚某高校A的绿地样方植被破坏后,植被未经人为再次干扰,自然状态下,15周以后盖度基本恢复到破坏前水平.经过16周,移动与电信营业厅、行政大楼、学生公寓宿舍区、体育馆足球场旁的草坪恢复盖度值分别为90.1%、86.1%、81.3%、78.5%,分别恢复到破坏前的104.6%、103.7%、101.4%、115.4%;其盖度恢复情况采用Logistic拟合曲线的拟合度分别为0.999、0.998、0.999、0.999,拟合优度都高度接近1,故Logistic曲线作为盖度恢复的相对生态数学模型,与丰度恢复模型曲线类型相同[4].

[1]Pielou E C. 数学生态学[M].卢译愚，译.北京:科学出版社,1988:2-35.

[2]李鹄鸣,王菊凤.生态对策影响种群增长的数学模型研究[J].生物教学学报,1994,9(4):207-213.

[3]刘利民,吴素文.生态学中的数学模型[J].沈阳农业大学学报,2000,31(3):295-299.

[4]王湘君,陈文,杜宇,等.三亚市区绿地生态破坏后丰度恢复的数学模型研究[J].琼州学院学报,2015,22(2): 90-94.

[5]牛翠娟,娄安如,孙儒泳,李庆芬.基础生态学[M].北京:高等教育出版社,2002:109-118.

[6]徐天华,马丽蓉,帅维成.一类含扩散时滞的生态模型的周期解存在与稳定性[J].广西民族大学学报(自然科学版),2009,16(3):51-53.

[7]王平建.城市绿地生态建设理论与实证研究[D].上海:复旦大学,2005:8-9.

Research of Coverage Restoration on Green Space in Sanya City Based on Mathematical Model

WANG Xiang-juna,b, CHEN Wenc, DU Yub.d, LI Mingd, FU Jia-leie, WANG Sheng-nana

(a. School of Tropic Eco-Environment Protection,b. Provincial Key Laboratory of Amphibious and Reptile Research, c. School of Food Science and Technology,d. School of Tropic Biology and Agronomy, e. Department of Mathematics,Qiongzhou University,Sanya Hainan,572022, China)

By using ecological mathematical models, the current research studied the coverage, the extent of spontaneous recovery, spontaneous recovery rate and spontaneous recovery difficulty of species after the species were damaged in Sanya city. Firstly, chosen were twelve natural grassland samples, 1 square meters each, in four sections on campus in University A. Then the whole surface vegetation was damaged within all samples and underwent natural restoration. It showed that the abundance restores after 15 weeks. The fitting degree of the logistic curve-ecological mathematics model of plant coverage recovery-is about 0.999.

green space ecology; natural restoration; coverage; mathematical model

2015-02-10

三亚市院地科技合作项目(2014YD31)三亚市区绿地生态破坏后恢复的数学模型研究;动物学海南省普通高等学校省级重点(扶持)学科资助(HNZ201502)动物生存环境研究;琼州学院校级青年教师科研基金项目(QZQN201444)

王湘君(1982-),女,重庆马南人，琼州学院热带生态与环境保护学院副教授,南京师范大学生态学专业2015级博士研究生，研究方向为生态学、动物学.

陈文(1980-),男,重庆马南人，琼州学院食品学院副教授,硕士,研究方向为化学.

X176

A

1008-6722(2015) 05-0086-05

10.13307/j.issn.1008-6722．2015．05．19