邻近交流线路时直流输电线下混合电场的计算

2015-03-14李铁鼎黄欲成秦澔澔

电力建设 2015年4期

李铁鼎，黄欲成，秦澔澔

(1. 中南电力设计院，武汉市 430071；2. 国网电力科学研究院，武汉市 430074)

(1. Central Southern China Electric Power Design Institute, Wuhan 430071, China;2. State Grid Electric Power Research Institute, Wuhan 430074, China)

邻近交流线路时直流输电线下混合电场的计算

李铁鼎1，黄欲成1，秦澔澔2

(1. 中南电力设计院，武汉市 430071；2. 国网电力科学研究院，武汉市 430074)

为了准确计算交直流并行输电线路线下混合电场，针对交流输电线路对直流导线表面电场的影响进行了分析，采用寻优算法优化模拟电荷位置，分析了直流导线表面电场随交流导线电压变化的情况。在考虑交流线路对直流线路空间离子轨迹影响的情况下，基于Deutsch假设计算了直流输电线路线下合成电场的瞬时最大值，提出了一种合理的假设，从而准确地计算了并行输电线路线下混合电场。最后分析了线路邻近间距对线下混合电场的影响。结果表明，交流输电线路对直流导线的起晕以及直流线下空间离子流场有较大影响，在计算时应予以考虑，交直流线路间距对直流线路线下混合电场有很大影响，在设计线路时应予以考虑。

交直流并行输电线路；混合电场；导线表面场强

0 引言

目前，输电系统的输电线路多为高压交流输电线路(high voltage alternating current，HVAC)，而随着高压直流(high voltage direct current，HVDC)输电系统的发展，输电线路走廊资源日趋紧张，为了节约输电走廊资源，HVDC输电与HVAC输电线路平行架设甚至同塔架设的情况可能出现。在输电线路设计、建设和运行过程中，需要考虑线路对电磁环境及周边生态环境的影响，如何在符合国家相关标准的前提下更合理、更经济地设计规划输电线路具有非常重要的现实意义。

在20世纪80年代就开始了交直流线路邻近情况的研究，但总体来说，对混合电场的计算方法仍不成熟。文献[1]采用基于Deutsch假设法计算了交直流混合离子流场，但并未对并行线下的混合电场进行讨论，只是进行了简单的叠加。文献[2]分析了交直流混合离子流场与直流离子流场中电荷运动轨迹的差异。文献[3]提出邻近交流线路的直流线路电晕损耗的计算方法，该方法假设交流线路只影响了直流线路的起晕场强，而未考虑其对空间离子流的影响情况。文献[4]基于Deutsch假设法对并行线路下的混合离子流场进行了计算，但并未考虑混合离子流场的时变特征。文献[5]提出了有限元-体积法计算混合电场，但是由于该方法的局限性，其未能完全反映交流导线电压变化对空间离子流的影响。文献[6]通过上流有限元法结合向后欧拉法，提出了同塔交直流混合电场的时域计算方法。但该方法未考虑直流标称电场分量受交流电场及离子流场的影响情况，仅取直流合成电场的瞬时值，未对直流电场的变化情况进行详细分析。文献[7]通过实验获得并行线路电晕电流特性，以此计算导线表面电荷密度随交流电压的变化规律。但由于缩小比例试验无法完全模拟实际情况，且电晕电流特性变化规律可能因环境的影响而发生变化，因此该方法实际应用效果有待商榷。

由于交流导线电压变化导致的直流导线起晕程度呈周期性变化，因此本文假设在1个周期内导线表面场强大于起晕场强时导线起晕且表面场强保持在起晕场强，当导线表面场强小于起晕场强时导线不维持起晕状态。

考虑到子导线间的相互作用，本文对每个子导线用1组模拟电荷精确模拟，且模拟电荷值随着交流导线表面电压不断变化，准确计算子导线表面在1个周期内的表面电场，基于Deutsch假设，分析交流导线对空间离子移动轨迹的影响，即对空间电力线轨迹的影响。通过合理假设，认为空间离子流场处于相对稳定状态，而直流标称电场随交流导线电压呈周期性变化，从而将稳定的空间离子流场与变化的直流标称场和交流工频场进行叠加，得到并行线路下的混合电场。最后利用该方法分析交直流并行时不同线路间距对地面混合电场的影响。

1 模拟电荷法计算导线表面电场

1.1 优化模拟电荷

考虑交流线路对直流线路的影响，在交流和直流子导线内均设置模拟电荷，将其放在同一个系统中进行计算。由于在模拟电荷法中模拟电荷的设置会对计算结果产生直接的影响，而模拟电荷数目及位置的设置有很大的主观因素，所以本文采用位置寻优算法对模拟电荷的位置进行优化，目标函数为

(1)

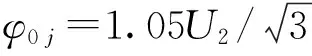
导线内部模拟电荷的设置如图1所示，其中r为子导线半径，a为导线内模拟电荷至导线表面的距离。设b=a/r，在1个周期内(0.02 s)每一时刻均对b以0.2为步长进行遍历，求得目标函数f的最优解及b值，以b±0.2为范围，以0.01为步长，求得目标函数f的最优解，直至目标函数满足工程计算的要求，即可达到对模拟电荷位置进行优化，求得最优位置的目的。

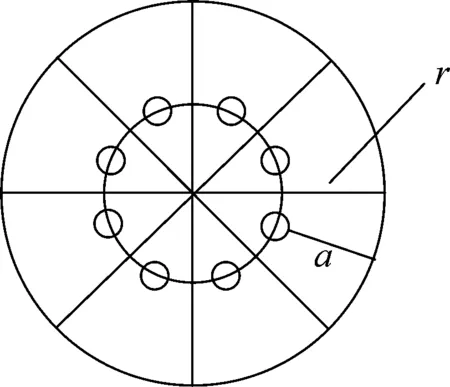
图1 导线内部模拟电荷的设置

2.2 计算导线表面电场

由于受到交流线路影响，直流线路子导线表面电场会随着交流线路进行周期性变化，利用皮克公式[6]估算导线的起晕场强，采用优化模拟电荷法计算1个周期内各时刻直流线路子导线各位置处的表面场强，确定子导线各位置在1个周期内的起晕时间。

2.3 基本方程和假设

考虑空间电荷的存在，根据电磁场基本理论可以得到描述直流线路离子流场的控制方程为[8-10]

(2)

(3)

(4)

式中：Es为空间合成电场；ρ为空间电荷密度；J为空间离子流密度；K为离子迁移率；ε0为空气介电常数。

在不影响计算结果可信度的情况下，为使计算简便，进行如下假设：

(1)Deutsch假设，即空间电荷只影响电场的幅值而不改变其方向。

(2)离子的迁移率是与电场无关的常数且正负离子的迁移率相等。

(3)不考虑离子的扩散，带电离子只受电场力的作用沿着电场线方向运动。

(4)忽略导线表面电晕层的厚度。

(5)交流线路影响空间电荷的移动，但不影响合成电场的幅值。

(6)在导线起晕期间内，其表面场强维持在起晕场强。

基于以上假设(1)，有

(5)

式中：E为标称电场；A为关于空间位置的标量函数。

在极导线表面的A值记为Ae，则

(6)

式中：Emax为子导线电荷发射点处最大表面场强；E0eq为子导线表面起晕场强，由皮克公式得到，粗糙系数取0.5。

记U为极导线的对地电压，则极导线起晕电压：

(7)

2.4 电力线的计算

合成电场的计算需要通过沿电力线利用割线法进行迭代，直至求出满足要求的结果。本文在文献[7]的基础上，改进了电力线的求解方法。在计算经过空间某点P(x,y)的电力线轨迹时，由于受到交流线路的影响，直流导线起晕具有间歇性，以直流导线表面场强最大时离子发射开始,计时间t=0，计算出离子到达P点的时间tp,以及此时刻P点在x，y方向的场强分量Ex,Ey，其中Ex，Ey分别包含了x，y方向的直流分量和交流分量。以时间步长Δt和空间离子迁移率K求步长L，则经过点P(x,y)的电力线上离点P(x,y)距离为L的点P1(x1,y1)的坐标为

(8)

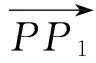
2.5 合成电场的计算

根据式(8)可得到电力线上每一点处x，y方向上的直流分量，即此处的标称电场值，则相邻2点的标称电位差即为

(9)

式中：Ezxi，Ezyi分别为第i个点上在x，y方向的直流分量。

由文献[11-14]可知

(10)

(11)

(12)

(13)

式中：ρm为沿电力线的加权平均电荷密度；φ1为该电力线上任一点处的电位。计算过程中的沿电力线积分问题均采用梯形公式。任意给定一个ρe的值，由公式(11)和(12)计算得到ρm，若该ρm与式(13)的值相等，则给定的ρe即为ρe的真实值，否则对ρe进行更新，迭代求解。

2.6 混合电场的计算

由于直流合成电场由标称场和空间离子流场叠加而成，因此本文将并行输电线下的混合电场分为3个部分：交流电场、直流标称场、空间离子流场[15-20]。由于直流导线受交流导线的影响，导致直流标称场也随时间成周期性变化，但是对于空间离子流场，本文假设其在直流导线起晕一定时间后达到一个相对稳定状态，在地面所产生的电场可以认为是一个恒定的电场。因此可以认为瞬时的混合电场由瞬时的交流电场及标称场与恒定的离子流场叠加产生。

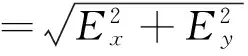
图2 计算流程图

3 算法验证

根据上述方法，使用Matlab软件编制了交直流并行输电线路线下混合电场的计算程序。以文献[14]中的实例进行验证，交流线路电压等级为500 kV，单回三角排列，导线型号采用4×LGJ-400/35，分裂间距为450 mm，直流线路电压为±800 kV，双极单回水平排列，导线采用6×LGJ-720/50型号，分裂间距为450 mm；交直流线路中心距离为40 m。具体线路结构尺寸如图3所示。

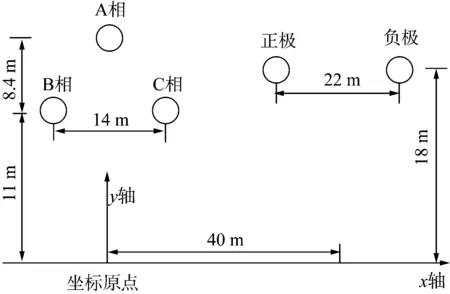
图3 交直流并行线路结构

直流线路导线表面测点如图4所示，r2为子导线半径，取直流线路正极2号分裂子导线作为对象，对其表面一周逆时针取点，以此分析距离交流线路最近的子导线表面电场随时间变化的情况，对2号子导线α=0°,45°, 90°,135°,180°,210°,240°等7个位置编号(基于子导线上下两面基本对称，场强值差别很小，以此选择不同的位置进行分析)，采用模拟电荷法计算其电场强度，具体如图5所示。

图4 直流线路子导线表面测点

从图5中可以看出，直流线路正极2号子导线0°,45°,90°位置处表面场强在1个周期内基本小于起晕场强，几乎不起晕，135°,180°,210°,240°位置处其表面场强会因为交流线路影响而不断变化。在A相电压相位角为200°左右时子导线表面场强达到最大值，此时刻的起晕程度最大。首先，本文从A相电压电位角为200°时开始，计算空间电荷从子导线表面起晕位置处出发的电力线轨迹，从而得到瞬时直流合成电场最大值，将其与瞬时的交流电场最大值进行叠加，获得瞬时的混合电场最大值，如图6所示。

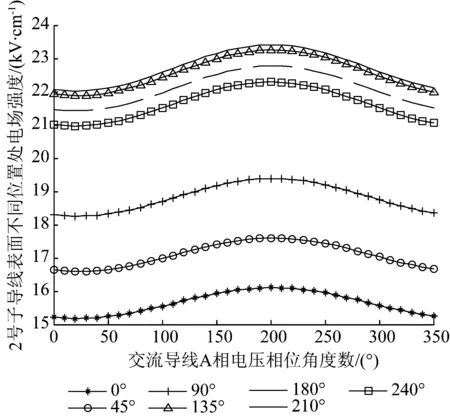
图5 2号子导线不同位置处表面电场随交流变化情况

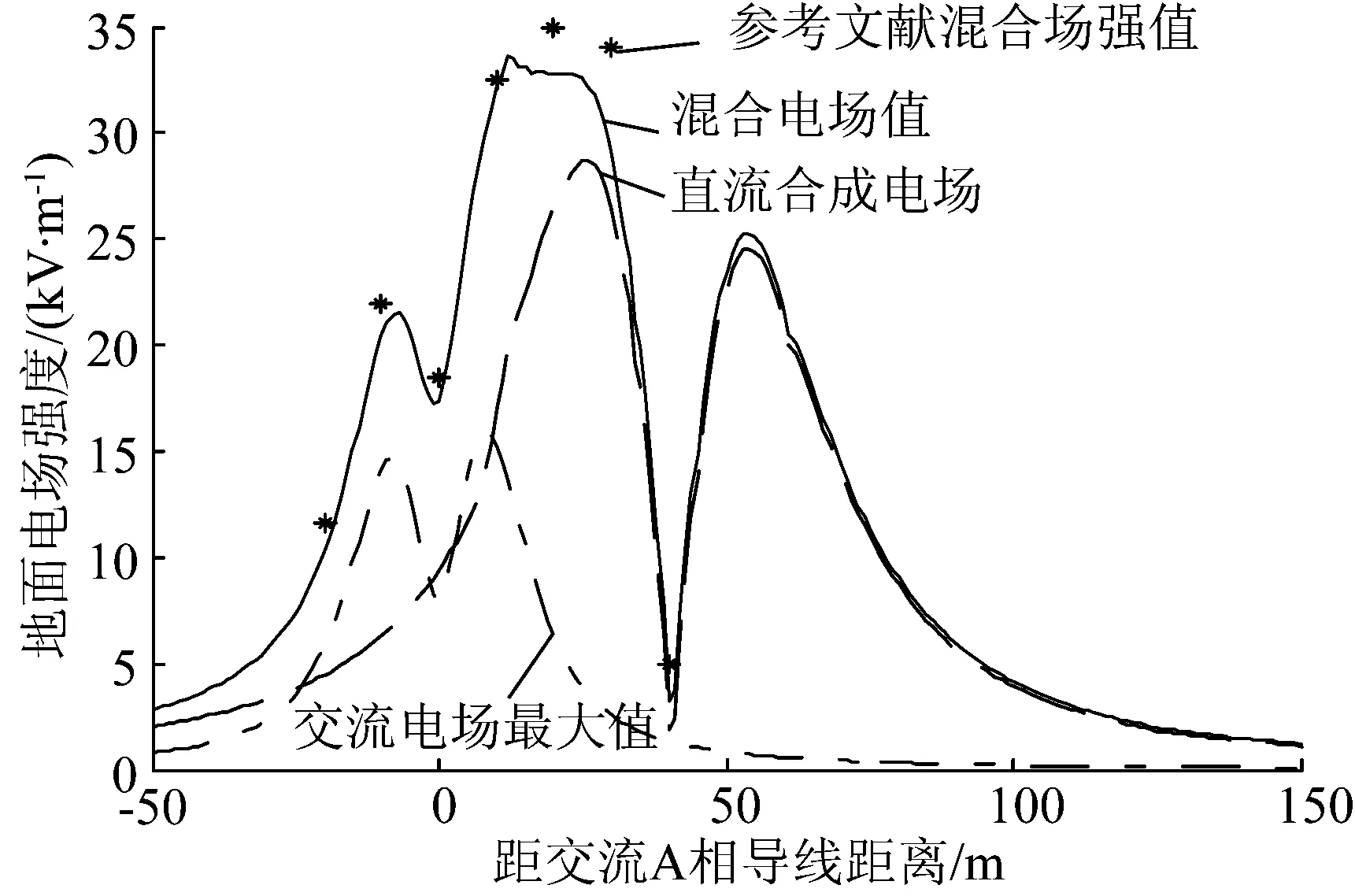
图6 地面混合电场强度

由于直流正负极导线下地面电场受交流导线的影响不同，为便于比较，取直流合成电场的绝对值来进行分析。表1给出了混合电场的计算结果并与文献[9]的数据进行了比较。

由表1和图6可知，程序计算结果与文献中的趋势基本一致，说明本文中对电力线轨迹的改进方法是有效的，本文中混合电场值偏小是由于文献未考虑交流线路对直流线路电力线轨迹的影响而直接进行了叠加，而本文将其考虑在内。

但是，对于地面直流合成电场和混合电场来说，直接采用瞬时值来计算和叠加是不符合实际的。因此，采用2.6节中的假设求得一个稳定的空间离子流产生的地面电场值，与直流标称场的瞬时最大值进行叠加，得到地面合成电场瞬时最大值，而混合电场的瞬时最大值则由交流电场与直流标称场叠加的瞬时最大值与稳定的空间离子流场进行叠加所得(邻近间距40 m)，如图7所示。

表1 本文混合电场值计算结果与文献值比较表

Table 1 Comparison of computation results of hybrid electric field with literature

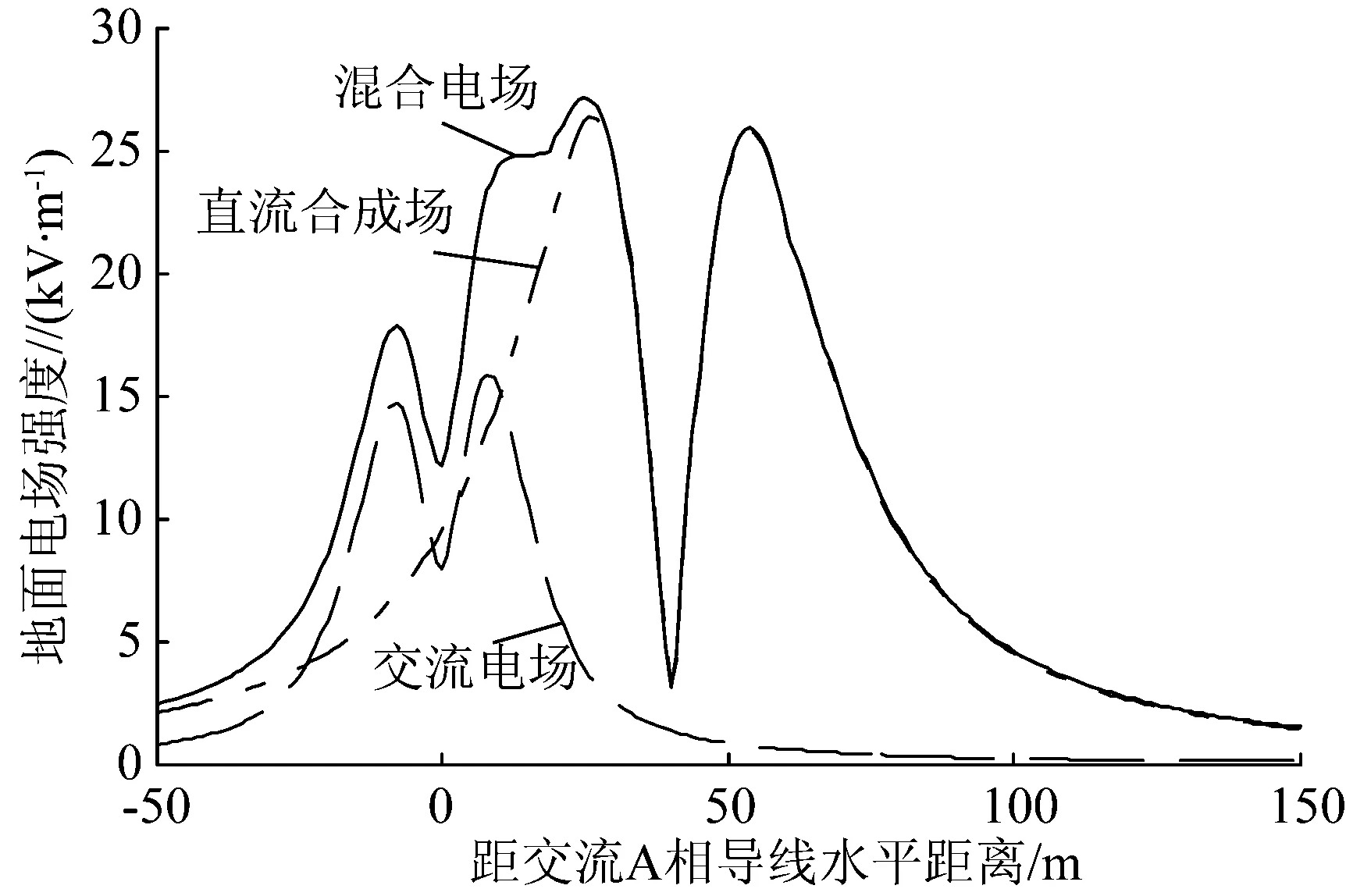
图7 地面混合电场强度

对比图6、7可知，直流合成场及混合电场都有所不同，主要原因在于：(1)图6中的直流合成场是以最大起晕时刻开始计算电力线轨迹，而图7中直流合成电场则是由稳定的空间离子流场与地面标称场的瞬时最大值叠加而成。(2)图6中的混合电场是瞬时直流合成场与交流场叠加的，并未考虑空间离子流所处的状态，且直流标称场的最大值与交流场的最大值并不是出现在同一时刻，电场方向也并不一致，不能直接叠加。本文取x=10 m处的交流电场及直流标称电场的变化情况来加以说明，如图8所示。

4 线路间距对直流线下合成电场及混合电场的影响分析

为了更好地节约输电走廊，合理布线，采用上述程序分析不同邻近间距时直流线路的起晕情况及线下场强大小。邻近间距为20、30 m的电力线分布如图9所示。

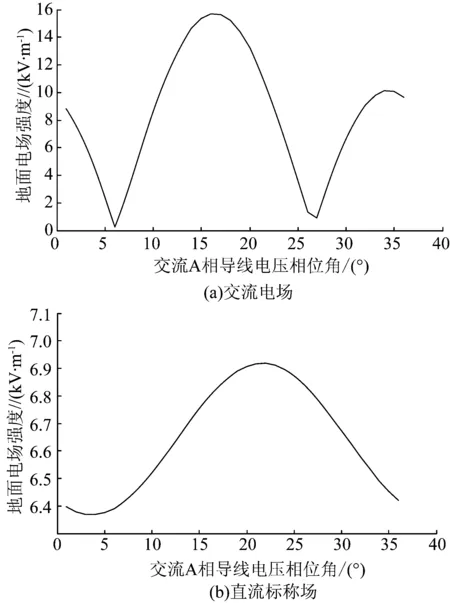
图8 x=10 m处交流电场和直流标称场1个周期内随时间变化情况

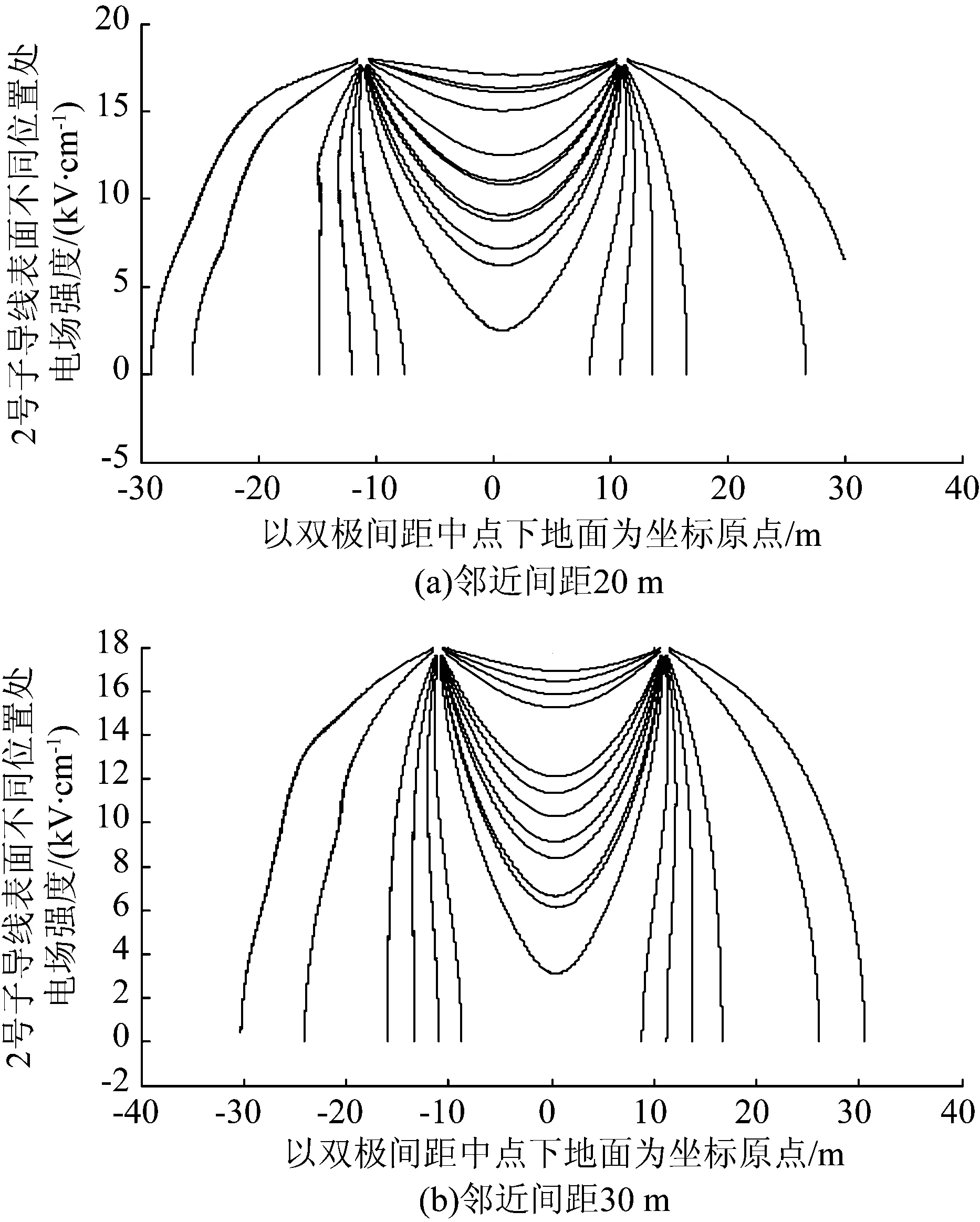
图9 邻近间距为20、30 m的电力线分布

由图9可知，交流线路对直流线路的电场线会产生影响，在利用Deutsch假设计算合成电场时不能简单地取交流电压瞬时值或有效值来计算，而应该在离子移动时考虑交流电场的变化对其产生的影响。因此，在计算电力线时需要每一步都更新交直流线路内设置的模拟电荷量，并重新计算该时刻空间的电场强度。

图10为不同邻近间距下2号子导线不同位置表面电场随A相电压相位角的变化情况。由图10可知，随着邻近间距的减小，正极2号子导线表面场强波动的幅值增大，将会导致子导线内侧不起晕的地方在1个周期内有一定程度的起晕，从而使得直流线下的空间离子流密度增大，地面合成电场增大。

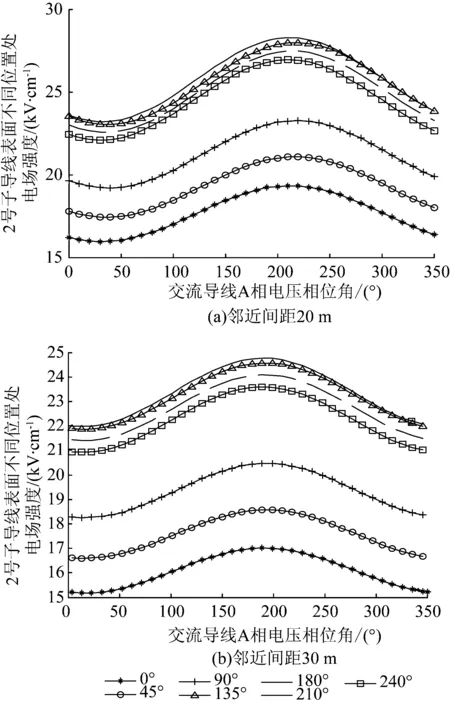
图10 不同邻近间距下2号子导线不同位置表面电场随A相电压相位角变化情况

图11为不同邻近间距的交流电场瞬时最大值，图12为不同邻近间距的地面合成场瞬时最大值。由图11、12可知，随着邻近间距的减小，邻近直流线路一侧的交流电场瞬时最大值明显增大，而邻近交流线路一侧的直流线路线下合成电场也明显增大。这是由于交流线路与直流线路的相互影响导致的。本文为了更好地表述直流线路正负极受交流的影响情况，取直流线下合成场强的绝对值来加以分析，可以更好地呈现邻近交流线路时正负极线路下地面电场的差异。

图11 不同邻近间距的交流电场瞬时最大值

图12 不同邻近间距的地面合成场瞬时最大值

图13为不同邻近间距地面混合电场强度瞬时最大值。由图13可知，随着邻近间距的减小，线路下的混合电场先增大后减小，与直流合成电场及交流电场的趋势不一致，这是由于直流标称电场的瞬时最大值与交流电场的瞬时最大值并不是出现在同一时刻，如图8所示，因此其混合电场并不是简单的两者叠加。尽管国家对混合电场的相关限值并未出台，但是在这种线路构架且其他参数不变的情况下，从图12中可以看出，间距应不小于40 m，以免混合电场强度超过30 kV/m。

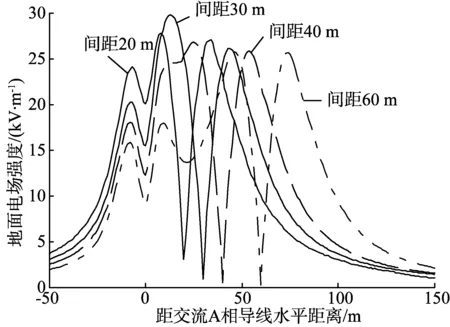
图13 不同邻近间距地面混合电场强度瞬时最大值

5 结论

(1)本文分析了交流线路对直流线下离子轨迹的影响，考虑了子导线受交流线路影响时在1个周期内的起晕时间段以及不同时刻空间标称电场的变化，对电力线的求解方法进行了改进，通过与文献值进行对比验证了方法的正确性。

(2)提出了一种假设：认为空间离子流场处于一个相对稳定状态，其产生的电场值恒定。混合电场的瞬时最大值可通过空间离子流场与交流电场和直流标称场的瞬时最大值相叠加求得。

(3)分析了线路邻近间距对输电线下直流合成电场和混合电场的影响。结果表明，随着邻近间距的减小，直流线路邻近交流线路一侧线下合成电场明显增大，混合电场先增大后减小。由于我国尚未出台交直流并行线路电磁环境相关标准，且尚未有明确的混合电场的计算方法，因此本文所提出的方法及假设可以为设计部门提供相应的参考，更好地解决并行输电线路设计相关问题。

[1]Maruvada P S, Drogi S. Fields and ion interactions of hybrid AC/DC transmission lines[J]. IEEE Transactions on Power Delivery, 1988, 3(3): 1165-1172.

[2]Abd-Allah M A, Alghamdi A S. Ion trajectories and corona effects at converting one circuit of a double circuit AC line to DC [C]//Power Engineering Society Summer Meeting. Vancouver, Canada: IEEE, 2001:1749-1753.

[3]ZHAO T, Sebo S A, Kasten D G. Calculation of single phase AC and monopolar DC hybrid corona effects[J]. IEEE Transactions on Power Delivery, 1996, 11(3): 1451-1463.

[4]杨勇.交直流同走廊线路的电场分析和计算[D]. 北京：北京航空航天大学，2008. Yang Yong. Analysis and calculation of the electric field under AC and DC transmission lines in the same transmission corridor[D]. Beijing: Beihang University, 2008.

[5]Yin H, He J L. Finite volume-based approach for the hybrid ion-flow field of UHVAC and UHVDC transmission lines in parallel[J]. IEEE Transaction on Power Delivery, 2011,26(4):2809-2820.

[6]赵永生，张文亮. 同塔交直流输电线路混合电场研究[J]. 电网技术，2014，38(1)：120-125. Zhao Yongsheng, Zhang Wenliang. Research on hybrid electric field caused by HVAC and HVDC transmission lines erected on the same tower[J]. Power System Technology, 2014, 38(1):120-125.

[7]周象贤. 高压交直流并行线路离子流场的计算方法研究及其应用[D]. 北京：华北电力大学，2013.

[8]刘振亚. 特高压直流输电工程电磁环境[M]. 北京：中国电力出版社,2009.

[9]Sunaga Y, Sawada Y. Method of calculating ionized field of HVDC transmission lines and analysis of space charge effects on RI[J]. IEEE Transactions on Power Apparatus and Systems, 1980, 99(2): 605-615.

[10]Yamazaki K, Olsen R G. Application of a corona onset criterion to calculation of corona onset voltage of stranded conductors[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2004, 11(4):674-680.

[11]Peek F W. Dieletric phenomena in high voltage engineering[M]. New York: McGraw-Hill, 1929.

[12]杨勇,陆家榆,雷银照. 同塔双回高压直流线路地面合成电场的计算方法[J]. 中国电机工程学报, 2008, 28(6):32-36. Yang Yong, Lu Jiayu, Lei Yinzhao. Calculation of the total electric field at ground level for double-circuit HVDC overhead transmission lines[J]. Proceedings of the CSEE,2008,28(6):32-36.

[13]罗兆楠，崔翔，甄永赞，等. 直流输电线路三维离子流场的计算方法[J]. 中国电机工程学报, 2010, 30(27):102-107. Luo Zhaonan, Cui Xiang, Zhen Yongzan, et al. A calculation method for 3-D ionizes field under HVDC transmission lines[J]. Proceedings of the CSEE, 2008, 28(6):102-107.

[14]鞠勇,吴桂芳. 特高压直流线路与交流线路同走廊时的电场研究[R]. 北京：中国电力科学研究院, 2007.

[15]张广洲. 交直流线路混合电场计算与测试研究[D]. 武汉：武汉大学. 2012. Zhang Guangzhou. Calculation and measurement of hybrid electric field from AC/DC lines[D]. Wuhan: Wuhan University, 2012.

[16]Li W, ZHANG B, He J L, et al. Calculation of the ion flow field of AC-DC hybrid transmission lines[J]. Generation, Transmission & Distribution, IET, 2011, 3(10): 911-918.

[17]周象贤，卢铁兵，崔翔，等. 邻近交流线路时直流输电线路电晕损失的计算与分析[J].中国电机工程学报, 2011, 31(31): 211-218. Zhou Xiangxian, Lu Tiebing, Cui Xiang, et al. Corona loss analysis of high voltage DC transmission lines in close proximity of high voltage AC transmission lines[J]. Proceedings of the CSEE,2011, 31(31):211-218.

[18]Al-Hamouz Z M. A hybrid computational technique for the estimation of corona power loss associated with bundled transmission lines[J]. Electric Power Systems Research, 1999, 50(1):65-70.

[19]Sarma M. Field and ion inter-actions of hybrid AC/DC transmission lines[J]. IEEE Transactions on Power Delivery, 1988,3(3):1165-1172.

[20]Bracken T D, Senior R S., Bailey W H.. DC electric fields from corona-generated space charge near AC transmission lines[J]. IEEE Transactions on Power Delivery, 2005, 20(2):1692-1702.

[21]Yin H, HE J L, Zhang B, et al. Finite volume-based approach for the Hybrid ion-flow field of UHVAC and UHVDC transmission lines in parallel[J]. IEEE Transactions on Power Delivery, 2011,26(4):2809-2820.

[22]Abdel-Salam M, El-Mohandes M T, EI-Kishky H. Electric field around parallel DC and multi-phase AC trans-mission lines[J]. IEEE Transaction on Electrical Insulation, 1990,25(6):1145-1152.

[23]Yang Y, LU J, and Lei Y. A calculation method for the hybrid electric field under UHAC and UHVDC transmission lines in the same corridor[J]. IEEE Transactions on Power Delivery, 2010,25(2):1146-1153.

[24]Li W, Zhang Bo, Zeng R, et al. Discussion on the Deutsch assumption in the calculation of ion-flow field under HVDC bipolar transmission lines [J]. IEEE Transactions on Power Delivery, 2010, 25(4):2759-2767.

(编辑:张小飞)

Hybrid Electric Field Calculation under AC-DC Parallel Transmission Line

LI Tieding1, HUANG Yucheng1, QIN Haohao2

To accurately calculate the hybrid electric field under AC-DC parallel transmission lines, this paper analyzed the impact of AC transmission lines on the surface electric field of DC conductor, used optimization algorithm to optimize and simulate the charge location, and analyzed the change of the surface electric field of DC conductor with the voltage of AC conductor. Considering with the impact of AC transmission lines on the space ion trajectory of DC transmission lines, the maximum instantaneous value of total electric field under DC transmission lines was calculated based on Deutsch hypothesis, and a reasonable assumption was proposed to accurately calculate the hybrid electric field under AC-DC parallel transmission line. Finally, this paper analyzed the impact of line spacing on the hybrid electric field. The results show that AC transmission lines have a great influence on the corona and space ion flow field of DC conductor, which should be considered in the calculation; the spacing of AC/DC transmission lines also has a great influence on the hybrid electric field of DC transmission lines, which should be considered in the line design.

AC-DC parallel transmission line; hybrid electric field; electric field of conductor surface

J=KρEs

Es=AE

U0=AeU

(1. Central Southern China Electric Power Design Institute, Wuhan 430071, China;2. State Grid Electric Power Research Institute, Wuhan 430074, China)

TM 154

1000-7229(2015)04-0083-08

10.3969/j.issn.1000-7229.2015.04.014

2014-11-25

2014-12-12

李铁鼎(1987)，男，硕士，工程师，主要从事高压输电线路设计研究工作；

黄欲成(1979)，男，本科，高级工程师，主要从事高压输电线路设计研究工作；