基于核的模糊C均值逐层聚类算法在负荷分类中的应用

徐衍会，张蓝宇，宋歌

(华北电力大学电气与电子工程学院，北京市 102206)



基于核的模糊C均值逐层聚类算法在负荷分类中的应用

徐衍会，张蓝宇，宋歌

(华北电力大学电气与电子工程学院，北京市 102206)

针对传统的模糊C均值聚类方法不适于非正态分布数据集的聚类、处理高维数据集收敛速度缓慢以及噪声点敏感的问题，提出了一种基于核的模糊C均值逐层聚类方法，应用于电力负荷特性分类。该方法的核心是2个模块和1个算法：改进快速排序法模块、核函数模块与模糊C均值算法。改进快速排序法模块将大数据集划分为若干特征突出的子空间，进而结合核函数模块与模糊C均值算法对各子空间进一步精确分类。以广东省的负荷调研数据为基础，在Matlab平台上对基于核的模糊C均值逐层聚类方法与模糊C均值算法的分类结果进行对比分析，结果表明：前者在提高分类效率与分类精确度的同时，具备较理想的收敛速度；另外，前者分类结果精细程度的可控性有利于电网工程实用规划。

负荷分类；改进快速排序法；核函数；模糊C均值

0 引 言

随着电网规模的逐渐扩大，国内一些大型省网作为典型的受端电网，多直流落点安全稳定性与受端地区电压稳定性成为影响电网安全稳定的重大课题。为了准确把握电网的运行特性，确保电网可靠地持续供电，电力系统数字仿真精确性的提高具有重要的现实价值。毋庸置疑，负荷模型的精确性直接影响仿真结果的准确性，而制约负荷模型建立的主要因素是由于负荷自身的随机时变性、地域分散性、成分多样性、非连续性等特点导致的综合负荷特性差异[1-3]，造成综合负荷特性差异的根本原因则是负荷构成成分的不同[4]。因此，按照负荷构成不同对其进行分类对建立结构合理、参数准确的综合负荷模型，以服务于电力系统仿真计算具有十分重要的意义。

我国各区域电网的变电站数目庞大且负荷组成多样化，负荷分类就是将同一电网负荷特征接近或相似的负荷点归并分类，按类分组进行建模。近年来，将模式识别领域的聚类分析应用于电网负荷分类大大推动了电力负荷分类精确化的发展。目前已应用于负荷分类的聚类方法有层次聚类算法和基于准则函数最优的聚类算法[5]，尤其以隶属于后者的模糊聚类算法得到了广泛关注。模糊聚类算法主要包含二大分支，基于模糊等价关系的传递闭包法(传递闭包法)和模糊C均值聚类算法(fuzzy c-means algorithm，FCM)。传递闭包法以模糊相似度为基础，得到模糊等价矩阵后设置阀值决定分类数目[6-7]，分类结果粗糙但计算速度明显优于FCM。FCM的聚类能力优于传递闭包法，目前针对FCM的改进优化研究主要集中在参数优化[8-9]与初始聚类中心选择[10-11]这2个方面。

虽然FCM更具备推广价值，但由于FCM受样本分布与初始参数的制约，在迭代过程中对噪声点敏感且易陷入局部最小[12-13]；另外，由FCM的迭代过程推出，算法对于球状分布的数据聚类效果较好[14]，而实际样本空间并非球状分布，严重制约了FCM的推广应用能力。

因此，本文提出基于核的模糊C均值逐层聚类(quick sort-kernel fuzzy c means, QS-KFCM)算法，引入逐层分类思想，在处理呈现不规则分布的大规模样本集时，首先将大样本集进行压缩，快速搜索归并突出特征相似的样本，划分为若干子空间，然后对各子空间进一步精确聚类，最终得到满足要求的分类结果。

1 QS-KFCM算法

1.1 改进快速排序法模块

利用改进快速排序法模块完成大样本集到子空间的划分是一次全局搜索的过程，将样本空间中的每个样本作为1条数据进行管理，提取每个样本的最大特征值，以最小的计算代价将具有相同突出特征的样本归入同一子空间，为子空间的精确分类做好基础分类工作。

快速排序法采用分治策略，平均时间复杂度为O(nlogn)[15]，考虑到本文只需提取数组最大元素，因此，对快速排序法进行改进，查找到最大元素后即可结束递归调用，时间复杂度小于O(nlgn)。

假设待排序的n个元素存储在数组A[0,n-1]中，选择A[0]作为基准元素，以此基准元素为中心，将当前无序区域划分为左右2个较小的子区间A[0,pt-1]和A[pt+1,n-1]，使得A[0,pt-1]中元素均小于A[0]，A[pt+1,n-1]中元素均大于A[0]，调整后A[0]所在位置设为pt。根据pt查找最大元素位置，判定是否输出：

(1)若pt=n-1，则终止递归调用，A[pt]=maxA[0,n-1]，输出最大值A[pt]；若pt=n-2，则终止递归调用，A[pt+1]=maxA[0,n-1]，输出最大值A[pt+1]。

(2)否则，循环调用快速排序算法对左、右子区间A[0,pt-1]和A[pt+1,n-1]排序搜索，至A[n-1]=maxA[0,n-1],输出A[n-1]。

1.2 核方法模块

核方法模块将低维空间的样本通过非线性映射到高维空间，改善了数据的空间分布使其易于线性划分，使得聚类准确度和精确度大大提高，实现了对FCM的二次优化。

样本xi={xi1,xi2,…,xiq}，从原q维空间映射到Q维特征空间的非线性映射形式为

(1)

式中Φ(x)=[Φ(x1),Φ(x2),…,Φ(xQ)]。

核函数定义为从原q维空间映射到高维Q维特征空间的非线性映射Φ的点积形式，表示为

对于所有的x,z∈X⊂Rq，

(2)

常用的基本核中，高斯核作为能够更加准确地还原原有数据分布状况的核函数，受到了最为广泛的应用。

高斯核定义为

(3)

式中σ为高斯核函数的宽度，控制核的灵活性。

1.3 基于核的FCM算法

基于核的FCM算法是在高维特征空间中，通过构造拉格朗日函数，迭代寻找1组聚类中心矢量，使各样本到聚类中心的加权距离平方和达到最小。

假设X={x1,x2,…,xn}⊃Rq是给定的数据集合，聚类中心vj(j=1,2,…,c)，c表示待分类数目，基于核的FCM聚类模型描述如下：

最小化

(4)

使得U∈M

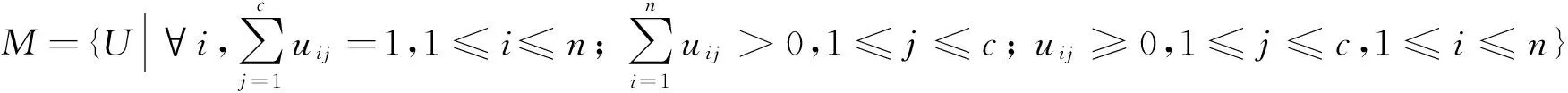
运用拉格朗日乘数法，建立无约束准则函数

(5)

进而根据式(3)确定过渡矩阵K

(7)

注意，矩阵中的元素k(xi,vj)<10-15时，使k(xi,vj)≈0，优化矩阵。

为使目标函数值达到最小，不断更新各类中心及隶属度矩阵各元素的值，隶属度uij与聚类中心vj的更新公式

(8)

(9)

2 变电站分类中QS-KFCM方法的应用

取变电站论域Xi={x1,x2,…,xn}，xi表示各变电站负荷构成特征向量；xi由xi1,xi2,…, xi5表征，分别为各变电站的工业负荷、农业负荷、商业负荷、居民负荷、其他负荷的组成百分比。具体步骤如下：

(1)利用改进快速排序法遍历Xi中的xi，查找xi的最大特征值xim(xim=max(xi1,xi2,…,xi5))，进而将所有样本分置于5个子空间中，第j(j=1,2,…,5)个子空间的样本共同特征为xim=max(xi1,…,xij,…,xi5)。设置进行下一层分类的子空间容量阀值θ，大于该值时方可进行子空间分类，避免样本容量过小而进行不必要分类。

(2)子空间分类。假设第y个子空间由N个样本组成，初始化样本构成矩阵：

1)设定算法所需各类控制参数，m=2，σ=0.1，设置迭代次数为T，迭代由k=0开始。

2)降噪处理。实际电网中存在大工业用户或者其他用户，在聚类计算中不可避免的成为噪声点，影响算法准确性，因此，在对变电站论域X进行分类计算前，首先进行降噪处理，将噪声点单独划为一区后再对其余部分进行分类。本文规定变电站向量的某个特征值大于90%时，该站划入噪声区。

4)按式(7)计算过渡矩阵K，如果∃l、j，使K中的k(xi,vj)=1，则令ulj，且对i≠l,uij=0。

5)按式(8)与(9)更新隶属度矩阵与聚类中心，若k=T,输出模糊分类矩阵U=(μij)N×C和C个聚类中心向量V={v1,v2,…,vc}。

6)按照最大隶属度原则，确定子空间分类结果。另外，在实际负荷分类中，不同区域电网负荷组成状况有所差别，应根据具体区域具体省份对精细分类后的结果进行微调整，合并一些相近类别。

3 实例验证

3.1 基于核的模糊C均值逐层聚类算法分类结果分析

本文中的实验数据取自广东电网6个供电局的负荷特性调查统计结果。按照基于核的逐层聚类算法，得到的分类结果为：

(1)以工业为主的变电站区域，工业比重在41%～86%，共50个变电站T1={B5,…,B16,B18,…,B39,B41,…,B47,B50,…,B57,B59,B60}；以商业为主的变电站区域,商业比重为38%，共1个变电站T2={B7}；以居民为主的变电站区域，居民比重在31%～57%，共5个变电站T3={B17,B40,B48,B49,B58}；大工业用户变电站与其他用户变电站区域，即工业比重与其他比重在90%以上的变电站TZ1={B1,B2,B3,B4}, TZ2={B61,B62}。

(2)T1进一步分为T1={T11,T12,…,T16}，共6类，得到聚类中心矩阵

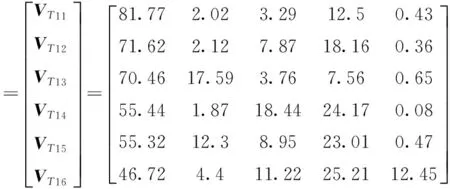
(3)T2中仅包含1个变电站，其居民用电与工业用电比重相当，各占30%，与T3中的多数变电站性质相似，因此将T2与T3合并为T23。

综上，将62个变电站分为9类：T11,T12,T13,T14T15,T16,TZ1,TZ2,T23。

3.2 QS-KFCM与FCM方法分类性能对比分析

4．统计学处理：采用SPSS17.0统计软件进行数据分析。计量数据先行正态性检验，符合正态分布数据以表示，组间比较采用独立样本t检验；不符合正态分布数据以M(P25，P75)表示，组间比较采用秩和检验。计数数据以例数表示，组间比较采用χ2检验。P<0.05为差异有统计学意义。

3.2.1 分类结果对比分析

采用相同聚类数目c=9，利用FCM算法进行计算，得到聚类中心矩阵

比较VQS-KFCM与VFCM，可得：

(1)工业比重较高区域，这2种算法得出的分类基本相同，这部分负荷特征突出，较易区分，工业比重在70%左右。

(2)VFCM中的V4与V7对应QS-KFCM算法分类结果中的T23类，代表了以居民为主或以商业为主的变电站区。

(3)工业比重在55%左右的区域，农业、商业占比差异较大，变电站特征分散，采用FCM算法只形成了V5这个中心点，农业比重为8%，商业比重为10%，但归入该类的变电站农业比重为0%～29%，商业比重为7%～20%，类内特征模糊；采用QS-KFCM算法形成了VT14与VT15这2个类中心点，分别归纳了工业比重为主、居民为辅的相同条件下，商业比重18%、农业比重2%与农业比重10%、商业比重10%的这2种情况，类内特征较为一致，类间特征差异较大。

(4)比较分类结果，存在较多差异，FCM算法的分类合理性较差，以B14与B57为例：FCM算法将B14([48,28,1.7,21,1.3])归入V3类，B58( [30,3,7,31,29])归入V6类，变电站特征显然与中心点不一致；QS-KFCM算法将B14归入T15类，体现出了该站各特征的比重关系，B58归入T23类，突出了该站以居民为主的特点，分类更加合理。

以上分析说明QS-KFCM算法可以实现变电站负荷分类工作；对于数量较少的以居民或商业为主变电站群，利用逐层分类的手段大大降低了计算复杂度和计算时间而不影响聚类精度；QS-KFCM提取变电站共同特征的能力优于FCM且能够全面概括不同类型的变电站组成特征，这与该算法不是随机选取中心点而是按照样本分布情况引导选择中心点，并且在迭代技术上采用基于核技术的FCM优化算法息息相关。QS-KFCM按照样本分布情况选择中心点并采用基于核技术的FCM进行迭代优化，从而其提取变电站共同特征的能力明显优于FCM，且能够全面概括不同类型的变电站组成特征。

本文采用Davies-Bouldin(DB)指标进行聚类有效性评价，同时计算出各类的类内致密度与类间离散度，比较两种算法的聚类精确度。

采用区的分类结果做对比实验，结果如表1～3所示。

表1 类内致密度对比

Table 1 Comparision of clustering density degree

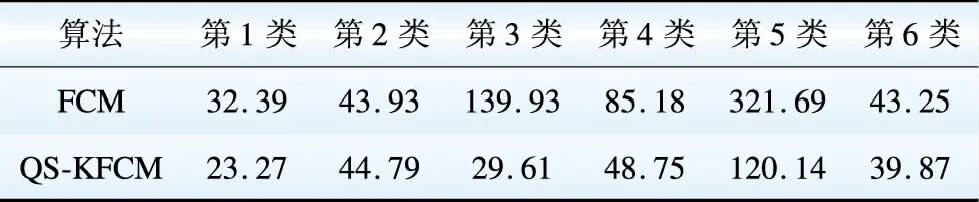
较好的聚类应使得类内分散度小而类间离散度高，表1、2表明，QS-KFCM算法的类内致密度比FCM算法高出近2倍，类间离散度也明显高于FCM算法。另外，DB值作为综合评价聚类有效性的指标，该值越小，表示聚类之间的相似性较小，类内相似性较高，聚类效果越好，由表3可以看出来QS-KFCM算法所得聚类结果精确度较FCM算法有很大的提升。

表2 类间离散度对比

Table 2 Comparision of clustering dispersion degree

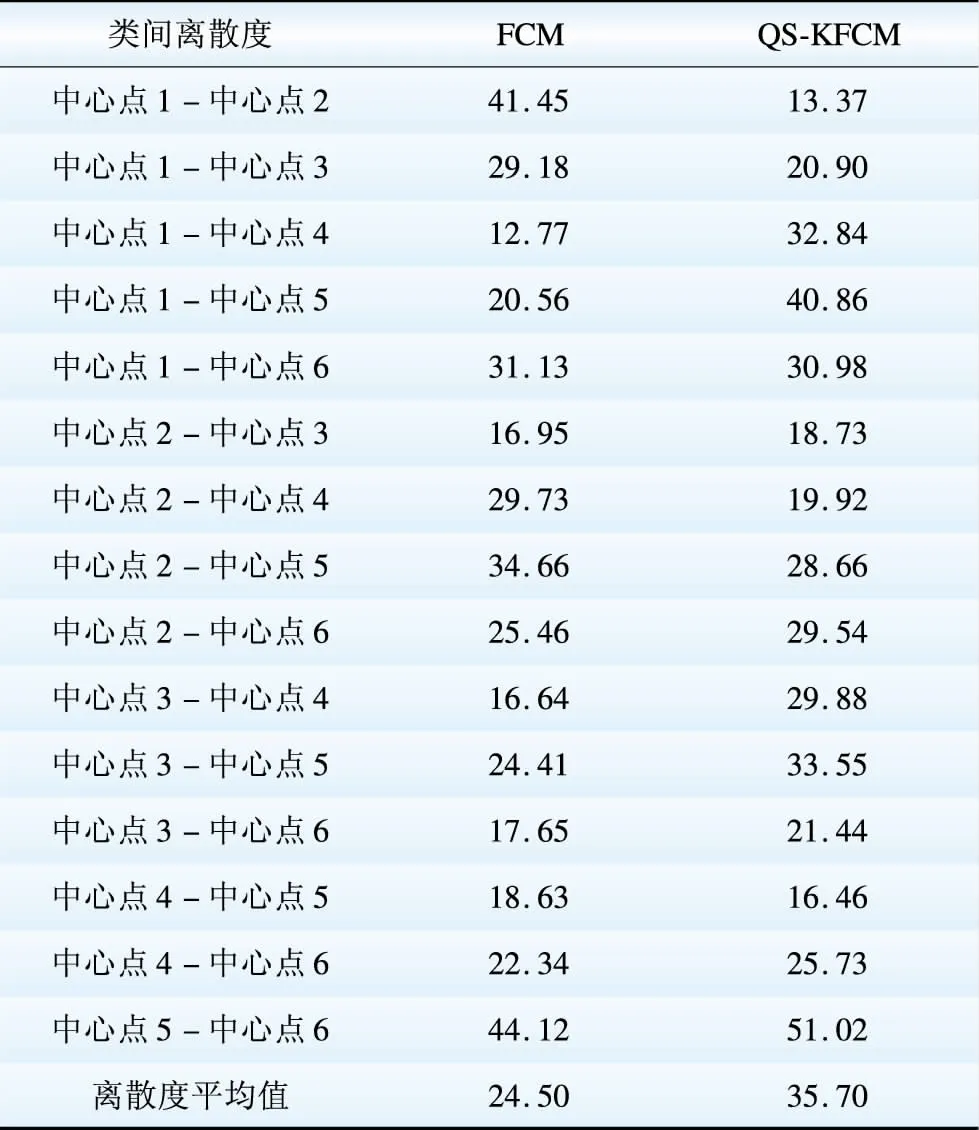
表3 DB值对比

3.2.3 对噪声点的抑制能力分析

考虑实际电网的变电站负荷特征各异，无法避免噪声点的存在，良好的聚类算法应具有较强的抗干扰能力。以工业为主的T1区变电站作为实验对象，分类数目为6，测试QS-KFCM算法与FCM算法对噪声点的鲁棒性,加入的噪声点分别取B1[100,0,0,0,0]与B55[31,1,38,30,0](B55以商业为主，与T1区变电站负荷特征差异较大)，分别作聚类分析。

首先加入B1，采用QS-KFCM算法该点不会影响T1区分类，由于该点达到降噪处理阀值，可通过降噪处理剔除，减少了不必要的计算时间。

其次，加入无法进行降噪处理的噪声点B55，进行聚类计算。表4为2种算法的中心点改变值，从加入噪声点的聚类中心与未加之前聚类中心的变化情况来看，FCM算法中心点偏离程度远大于QS-KFCM算法。观察2种算法对B55的隶属度分配情况(表5)，FCM算法将其硬性归入第6类，而QS-KFCM算法将B55的隶属度值平均分配给每一类，说明该点到各类距离接近，但不属于各类，借此隶属度分配特征可以检测出噪声点，另外，也使得该点对目标函数的影响得到了更好的抑制。

表4 噪声点对FCM、QS-KFCM中心点的影响

Table 4 Influence of noise on centroid of FCM, QS-KFCM

表5 噪声点在FCM、QS-KFCM算法中的隶属度分配值

该测试说明，具有降噪处理与核技术双重保障的QS-KFCM算法有很强的抵御噪声能力，使得该算法在处理不同类型数据结构时表现稳定。

3.2.4 收敛速度对比分析

目标函数值的变化直接反映聚类结果的收敛与否，精度越高的聚类结果应使得目标函数值越小，因此，采用FCM、QS-KFCM算法分别迭代计算52次，观察目标函数值变化。结果如图1所示。

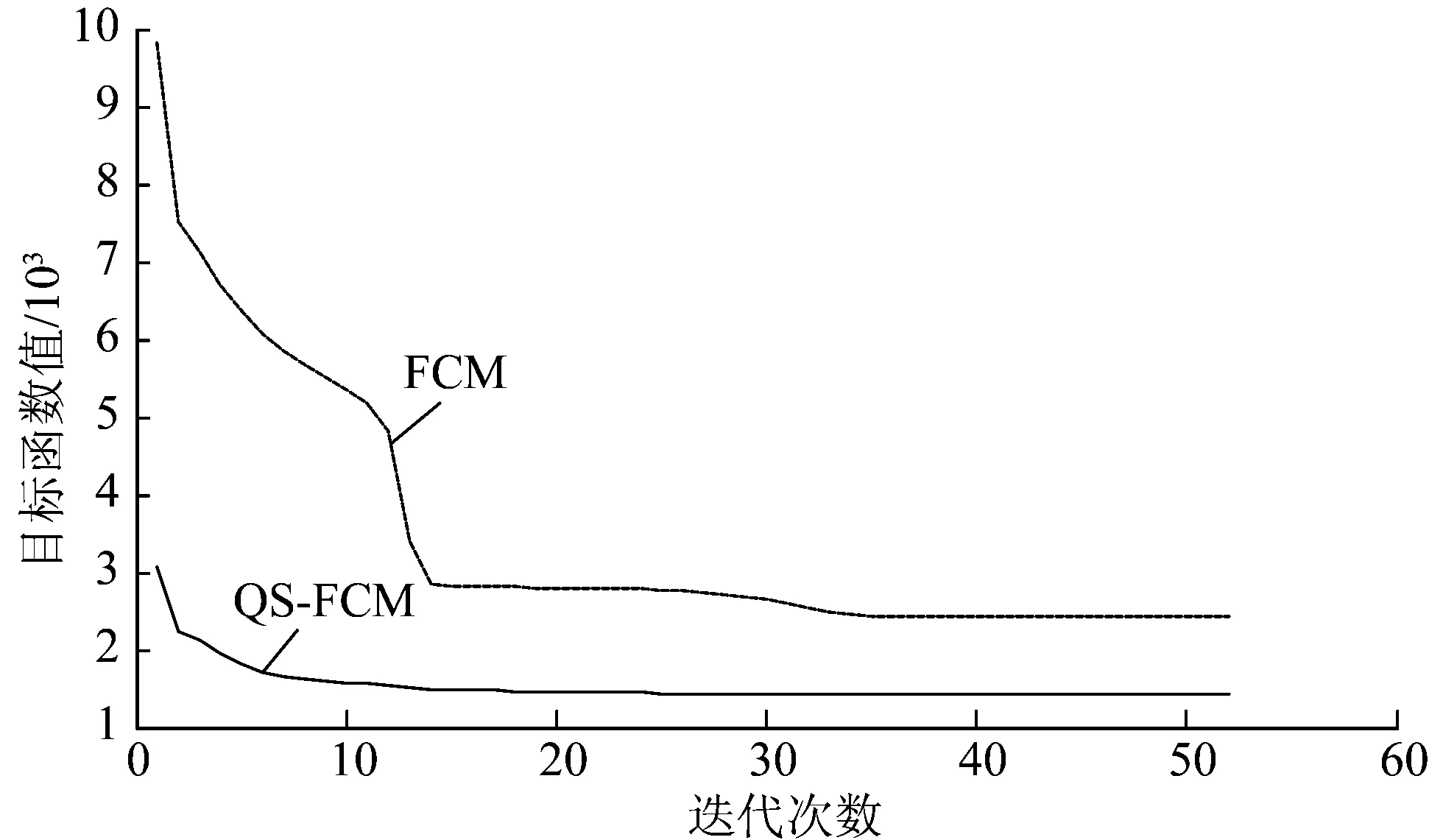
图1 QS-KFCM算法与FCM算法目标函数值

由图1可得：(1)QS-KFCM算法所得目标函数值收敛曲线一直处于FCM下方，目标函数值始终较小，这表明QS-KFCM算法选取的初始中心点比较符合实际分类状况，加快了收敛进程。(2)QS-KFCM的目标函数曲线在迭代10次后基本趋于稳定，说明目标函数值已收敛到最小； FCM的目标函数曲线在迭代15次开始平缓，到30次后才趋于稳定。意味着QS-KFCM算法的收敛速度相对较快，因此，可将前后2次的目标函数值之差的绝对值作为迭代终止条件，进一步优化QS-KFCM算法的计算速度。

4 结 论

本文主要针对模糊C均值算法处理大数据集收敛速度慢、聚类效果差以及噪声点敏感问题展开改进研究，提出了基于核的模糊C均值逐层聚类算法，并对广东省的负荷组成进行聚类分析。结果表明，该算法不仅增强了算法抵御噪声的能力和聚类准确度，而且有利于简化或降低负荷管理的难度和复杂性，实用性较强。但是，中心点的选择仍是下一步研究的重点，本方法采用的是均等划分的方法，具有一定的引导性质，而没有做到完全无监督分配，阻碍了分类结果的准确程度，尚需完善。

[1]贺仁睦, 魏孝铭, 韩民晓. 电力负荷动特性实测建模的外插和内推[J]. 中国电机工程学报, 1996,16(3): 151-154. He Renmu,Wei Xiaoming, Han Mingxiao. Power system dynamic load modeling based on the measurements in the field[J]. Proceedings of the CSEE, 1996,16(3): 151-154.

[2]贺仁睦, 韩冬，杨琳. 负荷模型对电网安全性的影响研究 [J]. 电网技术, 2007, 31(5): 1-5. He Renmu, Han Dong, Yang Lin. Study on effect of load models on power system security[J].Power System Technology,2007,31(5):1-5.

[3]郑晓雨．大电网实测负荷模型的实用化研究[D]．北京：华北电力大学，2011． Zheng Xiaoyu. Research on the praeticality of the measurement based load model in large grid[D]. Beijing: North China Electric Power University, 2011.

[4]李培强, 李欣然, 陈耀华, 等.基于模糊聚类的电力负荷特性的分类与研究 [J]. 中国电机工程学报, 2005, 25(24): 73-78. Li Peiqiang, Li Xinran, Chen Yaohua,et al. The characteristics classification and synthesis of power load based on fuzzy clustering[J].Proceedings of the CSEE,2005,25(24):73-78.[5]范九伦,赵凤, 雷博, 等. 模式识别导论[M]. 西安：西安电子科技大学出版社, 2012:79-91.

[6]黄梅,杨少兵. 负荷建模中的负荷调查统计分类[J]. 电网技术, 2007, 31(4): 65-68. Huang Mei, Yang Shaobing. Application study on load investigation and clustering for load modeling[J].Power System Technology,2007,31(4):65-68.

[7]黄梅, 贺仁睦, 杨少兵. 模糊聚类在负荷实测建模中的应用[J]. 电网技术, 2006, 30(14): 49-52. Huang Mei, He Renmu, Yang Shaobing. Application of fuzzy clustering in measurement-based load modeling[J].Power System Technology,2006,30(14):49-52.

[8]Maji P, Pal S K. Rough set based generalized fuzzy C-Means algorithm and quantitative indices[J].IEEE Transactions on Systems, 2007,37(6): 1529-1540.

[9]杨浩, 张磊，何潜，等. 基于自适应模糊C均值算法的电力负荷分类研究[J]. 电力系统保护与控制, 2010, 38(16): 111-115. Yang Hao, Zhang Lei, He Qian, et al. Study of power load classification based on adaptive fuzzy C means[J].Power System Protection and Control,2010,38(16):111-115.

[10]曾博, 张建华，丁蓝，等. 改进自适应模糊C均值算法在负荷特性分类的应用[J]. 电力系统自动化, 2011, 35(12): 42-46. Zeng Bo, Zhang Jianhu, Ding Lan, et al. An improved adaptive fuzzy c-means algorithm for load characteristics classification[J].Automation of Electric Power Systems,2011,35(12):42-46.

[11]周开乐, 杨善林. 基于改进模糊C均值算法的电力负荷特性分类 [J]. 电力系统保护与控制, 2012, 40(22): 58-63. Zhou Kaile, Yang Shanlin. An improved fuzzy C-means algorithm for power load characteristics classification[J]. Power System Protection and Control, 2012, 40(22): 58-63.

[12]Liu J W, Xu M Z .Kernelized fuzzy attribute C-means clustering algorithm[J].Fuzzy Sets and Systems,2008,159:2428-2445.

[13]朱晓清．电力负荷的分类方法及其应用[D]．广州：华南理工大学，2012． Zhu xiaoqing. Load classification method and its application[D]. Guangzhou: South China University of Iechnology, 2012.

[14]李晶皎，赵丽红，王爱侠. 模式识别[M]. 北京：电子工业出版社.，2010:87-95.

[15]黄江宁, 郭瑞鹏, 赵舫, 等. 基于故障集分类的电力系统可靠性评估方法[J]. 中国电机工程学报, 2013, 33(16): 112-121. Huang Jiangning, Guo Ruipeng, Zhao Fang, et al. Fault set classification method for power system reliability evaluation[J]. Proceeding of the CSEE, 2013, 33(16): 112-121.

徐衍会 (1978)，男，博士，副教授，主要研究方向为动态电力系统分析与负荷建模；

张蓝宇(1990)，女，硕士研究生，主要研究方向为负荷建模与负荷特性综合分析；

宋歌(1989)，女，硕士研究生，主要研究方向为负荷建模。

(编辑：蒋毅恒)

Application of Clustering Hierarchy Algorithm Based on Kernel Fuzzy C-Means in Power Load Classification

XU Yanhui, ZHANG Lanyu, SONG Ge

(College of Electrical & Electronic Engineering, North China Electric Power University, Beijing 102206, China)

To solve the problems that traditional Fuzzy C-means algorithm (FCM) was unsuitable for the clustering of non-normal distribution data set and sensitive to the noise, and its convergence speed for high dimensional dataset treatment was slow, a clustering hierarchy process based on kernel Fuzzy C-means algorithm was proposed for power load classification, which was composed of two modules and a algorithm: improved quick sort module, kernel function module and FCM. Firstly, an improved quick sort module was used to divide the large dataset into several subspaces with significant characteristics, then it could complete the clustering of subspaces combined with kernel function module and FCM algorithm. Based on the investigation data of load in Guangdong, the classification result of clustering hierarchy algorithm based on kernel Fuzzy C-means was compared with that of FCM on MATLAB platform. The results show that: the proposed method can improve the efficiency and accuracy of classification, and has higher convergence rate; moreover, the accuracy controllability of its classification results is benefited to grid engineering planning.

load classification; improved quick sort; kernel function; Fuzzy C-means

Φ:x∈X⊆Rq→Φ(x)⊆RQ

K(x,z)=<Φ(x),Φ(z)>

教育部中央高校基本科研业务费专项资金资助项目(2014MS05)。

TM 714

A

1000-7229(2015)04-0046-06

10.3969/j.issn.1000-7229.2015.04.008

2014-09-01

2014-10-30

Project Supported by the Fundamental Research Funds for the Central Universities (2014MS05).