二阶非线性不确定系统全局高速非奇异终端滑模控制

张凤宁（集宁师范学院　物理系，内蒙古　乌兰察布　012000）

二阶非线性不确定系统全局高速非奇异终端滑模控制

张凤宁
（集宁师范学院物理系，内蒙古乌兰察布012000）

摘要：终端滑模控制具有有限时间收敛、快速收敛、稳态精度高等优点，特别适用于快速、高精度控制，并在电机控制、飞行器控制等众多领域具有重要的应用价值.本文针对二阶非线性不确定系统有限时间鲁棒控制问题，为了提高终端滑模控制的控制性能，提出全局高速非奇异终端滑模及相应的滑模控制策略，并将新的滑模控制策略应用于二阶非线性不确定系统.所提出的全局高速非奇异终端滑模不仅具有非奇异快速终端滑模所不具备的全局高速收敛特性，而且可以提供全局非奇异性.

关键词：全局高速非奇异终端滑模；有限时间稳定；鲁棒控制

1　引言

随着我国现代化建设蓬勃发展，现代工业、环境控制乃至航空航天、国防工程，各行各业都越来越迫切需要高性能控制方法来实现更精确、更快速、更可靠的控制.终端滑模控制以其动态响应快、有限时间收敛、控制精度高、鲁棒性强等优点，在电机控制、机器人控制、卫星姿态控制等领域具有广泛的应用价值[1～4].非奇异快速终端滑模控制当系统状态远离原点时收敛速度快，且不具有奇异性[4].本文针对二阶非线性不确定系统控制问题，设计了全局高速非奇异终端滑模控制器.全局高速非奇异终端滑模不仅具有非奇异快速终端滑模所不具备的全局高速收敛特性，并且可以提供全局非奇异性.

2　全局高速非奇异终端滑模控制器设计

二阶非线性不确定系统的数学模型为：

其中，x（t)=（x1（t)，x2（t))T∈R2为系统状态，f1（x（t))、f2（x（t))和b （x（t))为系统状态的光滑函数，u（t)是控制量，d（t，x（t))代表不确定因素.

全局高速非奇异终端滑模控制器设计为：

其中，

γ∈（0，5，1)，i*=1，i*=2，β、ηi和hi属于R+，i=1，2.

全局高速非奇异终端滑模定义为：

全局高速非奇异终端滑模控制及全局高速非奇异终端滑模的调度策略为：

如果（Ξ（t))∈Ξi，则σ（Ξ（tτ))=i，其中i=1，2.

3　稳定性和收敛性分析

对于Ξ（t)∈Ξi，考虑李亚普诺夫函数

其中i=1，2.由（4)可得

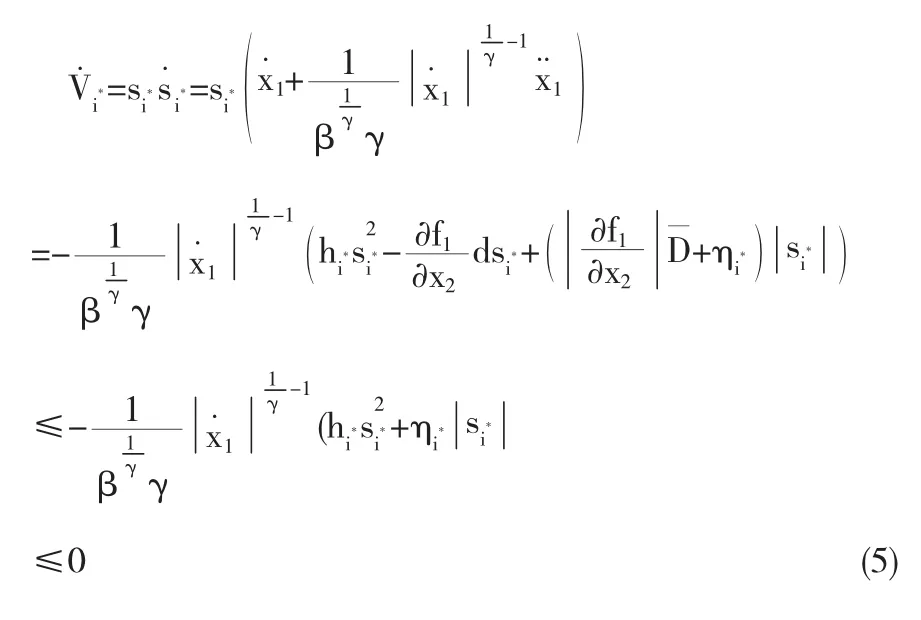
定义tR为系统状态到达滑模的时间，tS为系统状态到达滑模后沿滑模收敛到原点所用的时间.当系统状态到达全局高速非奇异终端滑模流形sG=0时，有x.1=-β|x1|γsgn（x1)或x.1=-βx1.对（3)积分，可得：

因此，系统状态在有限时间内到达全局高速非奇异终端滑模流形，并在有限时间内延全局高速非奇异终端滑模流形收敛到原点.

4　性能分析

非奇异快速终端滑模为：

其中，αNF=c^＞0，βNF=（2-γ^)/β^)1/（2-γ^)＞0.

如果系统状态到达滑模流形，且β=αNF+βNF，则当|x1|∈（1，+∞)时，有

|-βx1|=-|αNFx1-βNFx1|

＞|-αNFx1-βNF|x1|γNFsgn（x1)|

当|x1|∈（0，1)，γ=γNF时，有

|-β|x1|γsgn（x1)|=|-αNF|x1|γsgn（x1)-βNF|x1|γsgn（x1)|

＞|-αNFx1-βNF|x1|γNFsgn（x1)|

因此，所提出的方法具有高速收敛特性.

因为当x（t)∈Ξ1时，γ＞0.5，故本文方法不具备奇异性.

5　结论

针对二阶非线性不确定系统控制问题，为了提高终端滑模控制性能，提出了全局高速非奇异终端滑模控制器.该方法提高了全局收敛速度，且不具有奇异性.

参考文献：

〔1〕Z. Man，A. P. Paplinski，H. R. Wu. A robust MIMO terminal sliding mode control scheme for rigid robotic manipulators [J]. IEEE Transactions on Automatic Control，1994，39(12)：2464-2469.

〔2〕Y. Feng，X. Yu，Z. Man. Non-singular terminal sliding mode control of rigid manipulators[J]. Automatica，2002，38(12)：2159-2167.

〔3〕X. Yu，Z. Man. Fast terminal sliding -mode control design for nonlinear dynamical systems [J]. IEEE Transactions on Circuits and Systems I：Fundamental Theory and Applications，2002，49(2)：261-264.

〔4〕H. Li，L. Dou，Z. Su. Adaptive nonsingular fast terminal sliding mode control for electromechanical actuator [J]. International Journal of Systems Science，2013，44(3)：401-415.

基金项目：内蒙古自治区高等学校科学技术研究一般项目（NJZY13279）

中图分类号：TP242

文献标识码：A

文章编号：1673-260X（2015）09-0014-02