取值于局部凸空间向量测度的变差、半边差与有界性

乌仁其其格，杨梅荣（赤峰学院　数学与统计学院，内蒙古　赤峰　024000）

取值于局部凸空间向量测度的变差、半边差与有界性

乌仁其其格，杨梅荣
（赤峰学院数学与统计学院，内蒙古赤峰024000）

摘要：提出取值于局部凸空间向量测度的p-变差与p-半边差的概念，通过给出有关p-变差与p-半边差的几个结论，给出了取值于局部凸空间有界向量测度族一致有界的充分条件.

关键词：局部凸空间；向量测度；p-变差；p-半边差；Nikodym有界性定理

1　预备知识

2有关p-变差与p-半边差的几个结论

容易验证，取值于局部凸分离空间的向量测度F的每个变差和半变差具有下列性质：

（1）变差|•|p和半变差||•||p具有单调性；

（2）变差和半变差具有非负性；

（3）变差|•|p具有有限可加性，半变差||•||p具有半可加性；

（4）对任意的E∈F有||F||p（E)≤|F|p（E).

其中（4）的证明如下

||F||p（E)=sup{|x*F|（E):x*∈B（X*（p))}

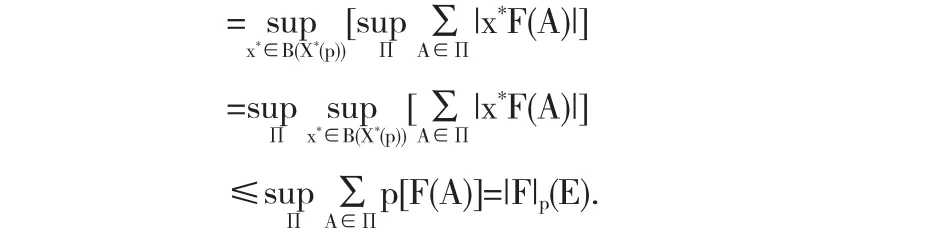
例1.1取值于局部凸分离空间向量测度的例.

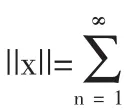
F（E)=（μn（E))，∀E∈F

显然F是取值于ω上的向量测度.

一般的，设{μτ:τ∈T}是有限可加数值测度族.KT表示所有函数f:T→K构成的线性空间，赋予点点收敛拓扑是完备的局部凸分离空间，定义F:F→KT如下

F（E)（τ)=μτ（E)，∀E∈F，τ∈T

F是取值于KT上的向量测度.

引理1.2对任意的x*∈X*（p)和x∈X，有|x*（x)|≤||x*||pp （x).

证明

引理1.3设（X，P)是局部凸分离空间，则对任意的p∈P和x∈X，有

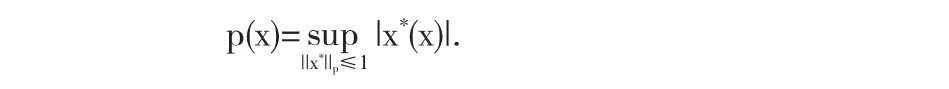
定理1.4设（X，σP)是局部凸分离空间，F:F→X是向量测度，p∈P，E∈F则

（2）sup{p[F（H)]:H⊂E，H∈F}≤||F||p（E)≤4sup{p[F（H)]:H⊂E，H∈F}

证明（1）设p∈P，E∈F

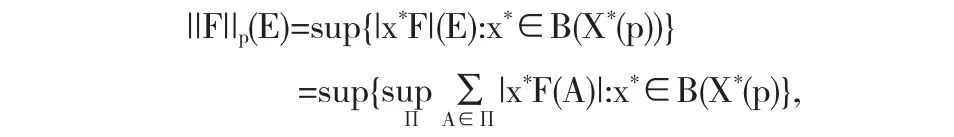
对每个A∈Π令

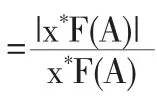
这样|εA|≤1，且

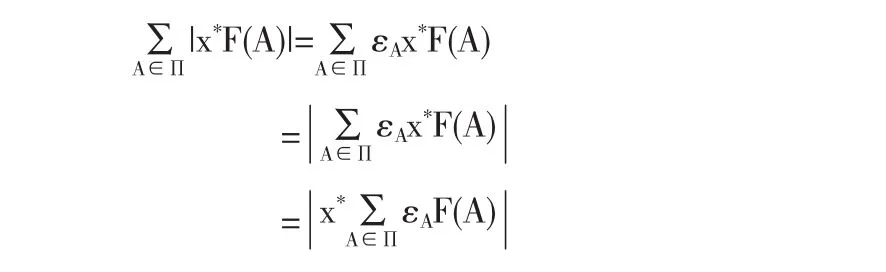
因为x*∈B（X*（p)根据引理1.2有

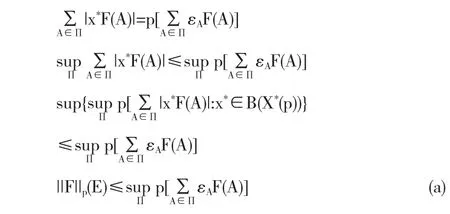
又根据引理1.3对E的任意F分划和满足条件|εA|≤1的有限族{εA，A∈Π}，有

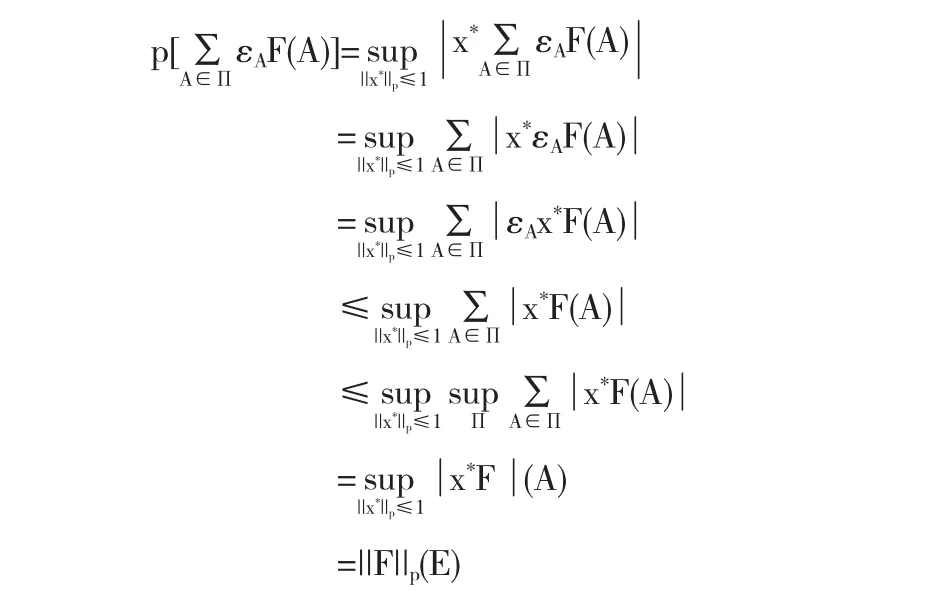
所以

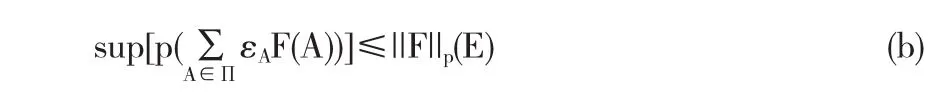
||F||p（H)≤||F||p（E)

故

sup{p[F（H)]:H⊂E，H∈F}≤||F||p（E).

对任意的x*∈B（X*（p)，设Π是E的关于F的任意分划，当X是实的局部凸分离空间时，记

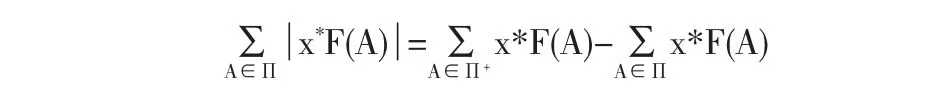
这里Π+是使x*F（A)＞0的集合A构成的有限族，Π-是使x*F（A)≤0的集合A构成的有限族

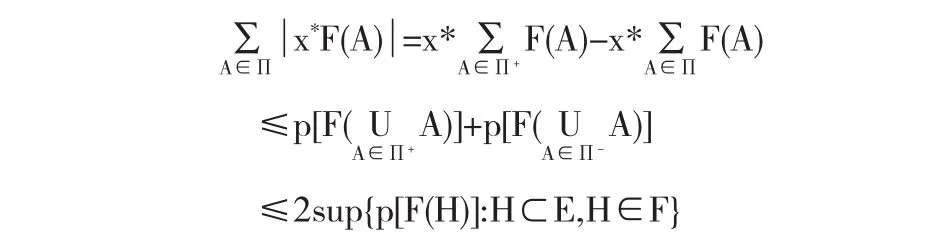
当X是复的局部凸分离空间时

x*F（A)=x1*F（A)-ix2*F（A)

其中x1*F（A)表示x*F（A)的实部，x2*F（A)表示x*F

（

A)的虚部，我们有||x1*||p≤||x*||p≤1，||x2*||p≤||x*||p≤1，所以

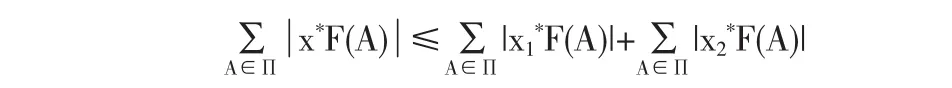
≤4sup{p[F（H)]:H⊂E，H∈F}

这样

||F||p（E)≤4sup{p[F（H)]:H⊂E，H∈F}

从而

sup{p[F（H)]:H⊂E，H∈F}≤||F||p（E)

≤4sup{p[F（H)]:H⊂E，H∈F}

参考文献：

〔1〕武立中，孙立民.局部凸空间上矢值测度某些有界变差的等价性.哈尔滨工业大学自然科学学报，1995(4).

〔2〕孙立民.取值于局部凸空间矢值测度的几个性质.哈尔滨师范大学自然科学学报，1996(4).

〔3〕J.DiestlandJ.Uhl，VectorMeasures，Math.Surveys，Vol.15，Am. Math.Soc.Providence，1997.

〔4〕Wilansky.A，Morden Methods in Topological Vector Spaces，New York：Mc GranHill，1978.

〔5〕Halmos p.R.Measure theorey，New York：Springerverlag，1974.

〔6〕林敏.对局部凸空间凸性和光滑性的探讨[D].内蒙古大学，2002.

〔7〕Taylor，A.E. Introduction to Functional Analysis，～NewYork.John Wiley &sons 1958.

〔8〕Wilansky.A，Mordern Methods in Topological Vector Spaces，New York：Mc GranHill，1978.

〔9〕Christopher E.Stuart，Paul Abraham Generalizations of the Nikodym boundedness and Vitali-Hahn-Saks Theorems J.Math.Appl.300(2004)351-361.

〔10〕D.R.LEWIS，Integration with respect to Vector Measures Pacific Journal of Mathematics，Vol.33，No. 1，1970.

中图分类号：O177.99

文献标识码：A

文章编号：1673-260X（2015）09-0005-02