地震作用下集装箱结构力学性能分析*

查晓雄 左洋 刘乐 王新捷

（哈尔滨工业大学深圳研究生院，广东 深圳 518055）

地震作用下集装箱结构力学性能分析*

查晓雄 左洋 刘乐 王新捷

（哈尔滨工业大学深圳研究生院，广东 深圳 518055）

针对目前广泛应用的多层集装箱房屋，提出了一种基于箱体之间摩擦耗能的滑移隔震体系.首先，建立了结构滑移隔震模型，并利用结构随机振动理论分析推导了层层滑移隔震结构各层等效阻尼比与摩擦系数之间的关系；然后，利用Abaqus非线性有限元软件建立了六层集装箱模型，对隔震结构、采用规范阻尼比的非隔震结构和采用等效阻尼比的非隔震结构分别在强震作用下的动力反应进行了弹塑性时程研究，分析了结构顶点位移、结构层间位移角以及结构层间滑移量等相关指标。结果表明：滑移隔震体系能有效减小结构各层最大位移；隔震结构和采用等效阻尼比的非隔震结构的最大层间位移角远小于采用规范阻尼比的非隔震结构；地震波的频谱特性会明显影响层层滑移隔震结构的动力反应.

多层集装箱房屋；地震作用；隔震体系；滑移；等效阻尼比；力学性能

多层集装箱房屋作为一种轻型钢结构被越来越多地用于房屋建筑中，集装箱用于建筑工程有许多优点并且用途广泛［1］.

国内外研究者在集装箱房屋方面开展了大量的研究，文献［1-7］主要对集装箱的建筑发展背景、演变过程、建筑造型形式等进行了介绍，同时还给出了典型集装箱建筑的施工操作过程、空间布局、室内外装饰装修以及集装箱建筑的环保特点等.文献［8-19］主要介绍了集装箱房屋的静动力性能，对其进行了整体和开洞的静力试验研究、抗冲击试验研究、抗风的有限元模拟等.

但是，目前关于集装箱房屋的研究大多数是基于建筑设计的角度；关于集装箱力学性能的研究较少，仅有的一些关于集装箱力学性能研究的文献，要么是缺乏试验验证，要么是局限于海运方面.对于多层集装箱整体抗震性能研究的缺乏严重制约了多层集装箱房屋的应用和发展.

文中主要研究了多层集装箱房屋的抗震性能，首先建立了六层隔震体系运动方程，并将其做线性等价处理，利用随机振动理论将线性等价后的误差项最小化，并推导了其中的速度均方差，从而得到了任意层的等效阻尼比；然后，利用有限元法对其进行了结构各层最大位移、各层位移角、各层滑移量等的分析，对之前的理论分析进行验证.本研究可为目前正在广泛应用的集装箱房屋提供设计施工参考，并可为相关的规范编制提供依据.

1 理论分析

1.1 六层隔震体系运动方程

在建立运动方程时做了以下几个假定：摩擦力采用库伦摩擦，在结构运动过程中摩擦力始终是一个定常数；结构滑移过程中不考虑结构倾覆；仅考虑水平地震作用；假定各角件处滑移空间足够大；假定摩擦系数很小，结构在地震荷载作用下处于滑动状态.结构模型如图1所示.图1中：m为集装箱质量；ci为集装箱阻尼；ki为集装箱刚度；i为序号.

图1 结构滑移隔震模型Fig.1 Structure sliding isolationmodel

根据图1，对结构建立动力运动方程，如式（1）所示：

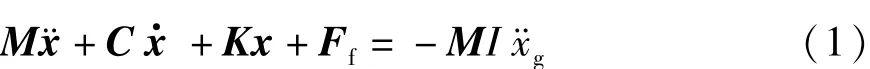
式中：M为结构集中质量矩阵；C为结构阻尼矩阵；K为结构刚度矩阵；Ff为每层集装箱所受层间摩擦力；x为每层集装箱相对于地面的位移，x= [x1x2x3x4x5x6]T；I为单位列向量，I= [1 1 1 1 1 1]T；为地震地面运动加速度.

其中：

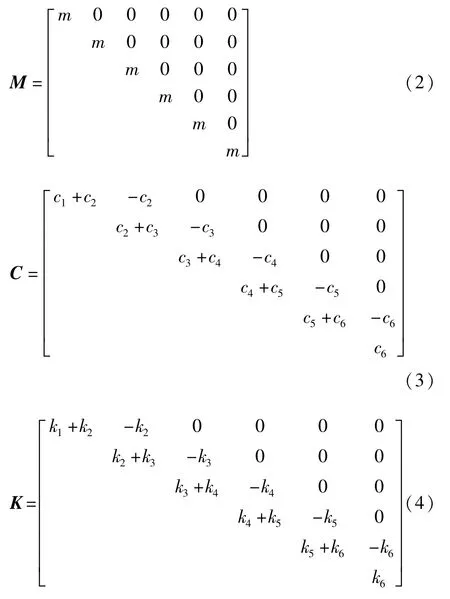
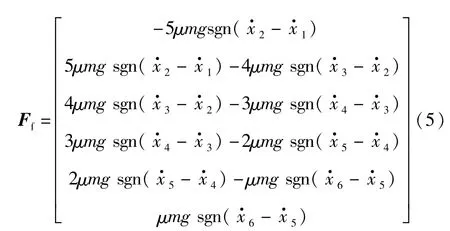
式中：μ为层间摩擦系数；g为重力加速度；sgn（x）为符号函数，当x＞0时，sgn（x）=1，当x=1时，sgn（x）=0，当x＜0时，sgn（x）=-1.

为方便起见，令：x2-x1=μ2，x3-x2=μ3，x4-x3= μ4，x5-x4=μ5，x6-x6=μ6，则式（1）可转化为

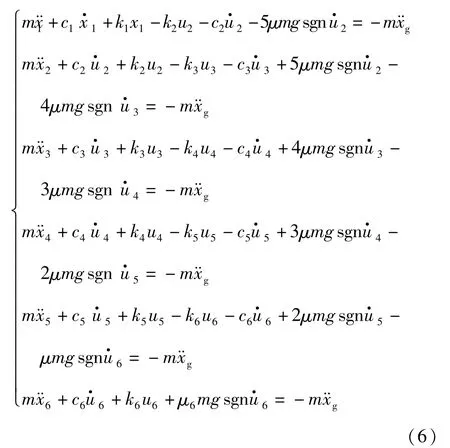
1.2 运动方程线性等价

运用线性等价方法将式（6）转化为线性等价方程组，如式（7）所示.

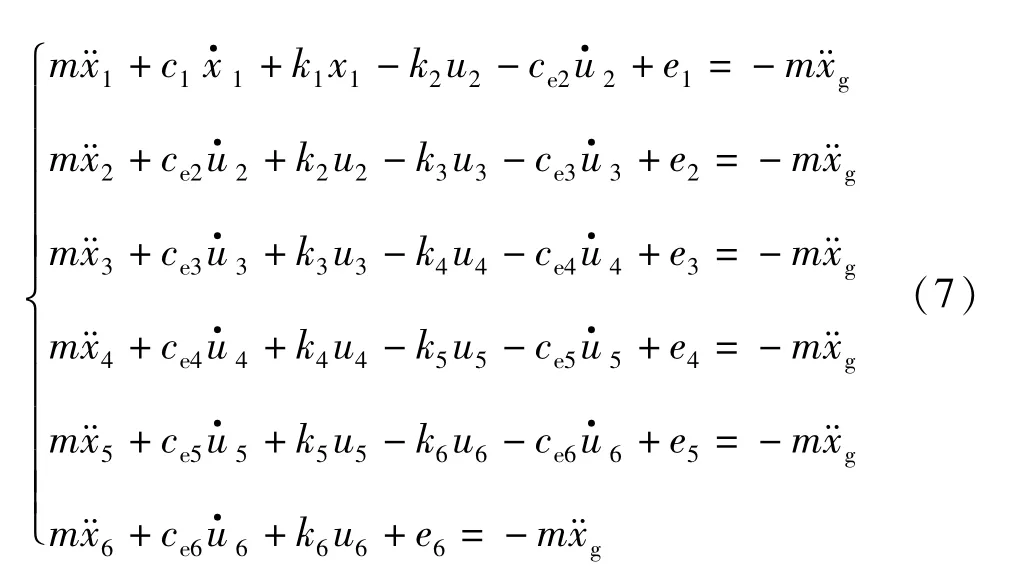
式中：cei为结构第i层等效阻尼；ei为结构第i层线性等价时产生的误差，可以表示为：

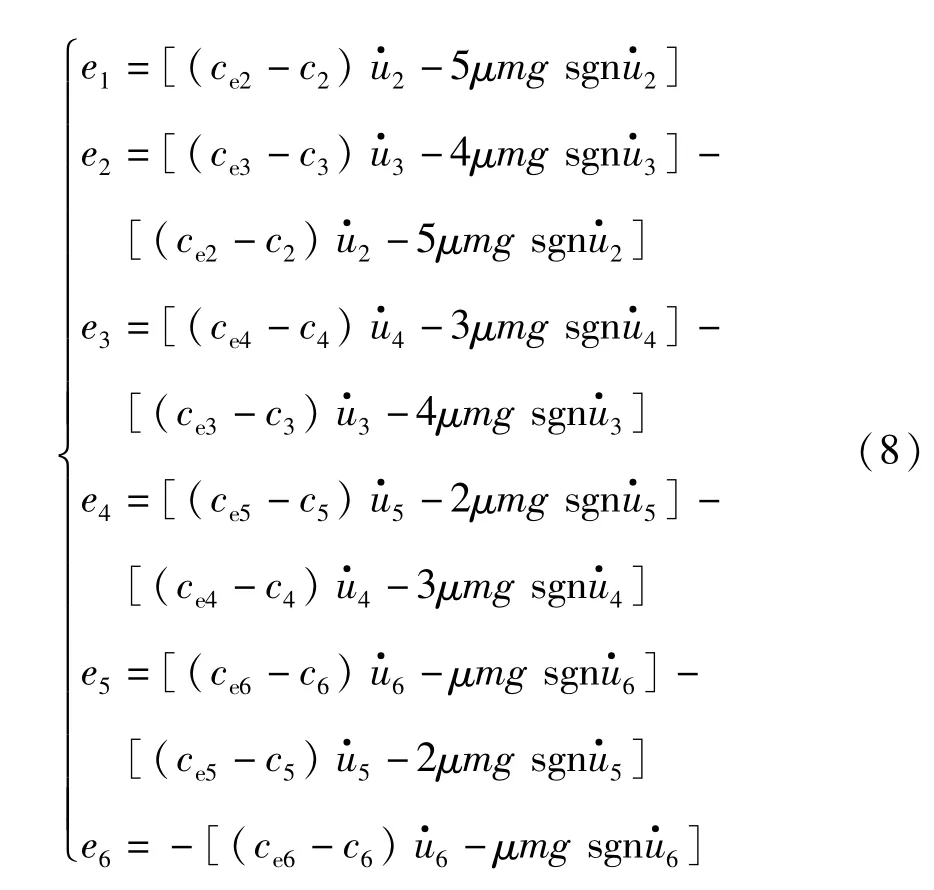
1.3 误差最小化

因为误差项ei越小，式（7）解得的结果误差也将越小，当误差项ei可以忽略时，式（7）就是线性方程组，所以有必要将ei最小化，具体过程如下.

1.3.1 对误差项e1平方的期望求偏导

对误差项e1平方的期望求偏导：

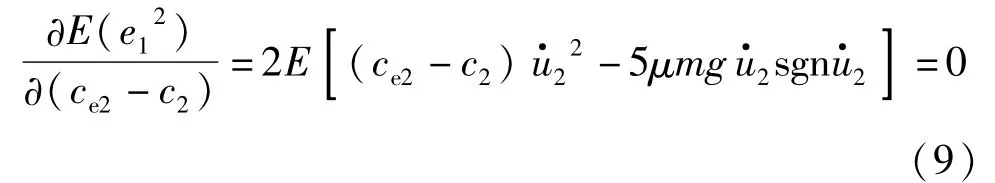
根据文献［20］可得：

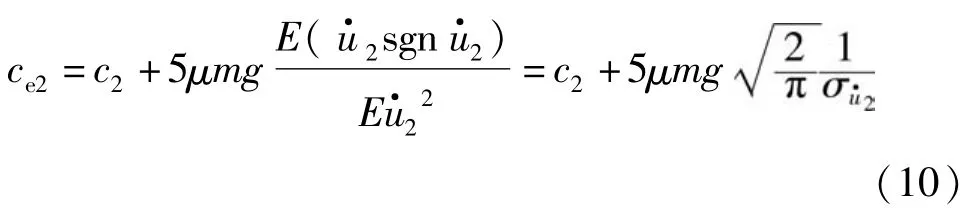
又由式（9）得：

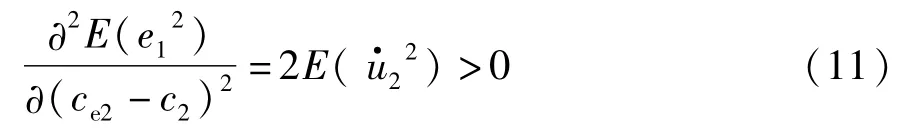
由误差项e1平方的期望求偏导可知，当式（9）成立时，e1取最小值.因此假设e1=0，则由式（8）和式（10）可得式（12）：

1.3.2 对误差项e2平方求偏导

对误差项e2平方求偏导：

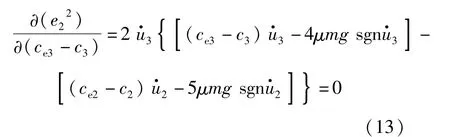
又由e1可得：

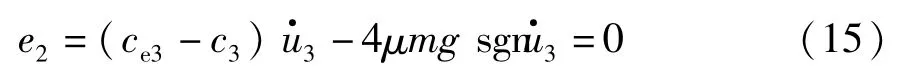
从而推导得到：

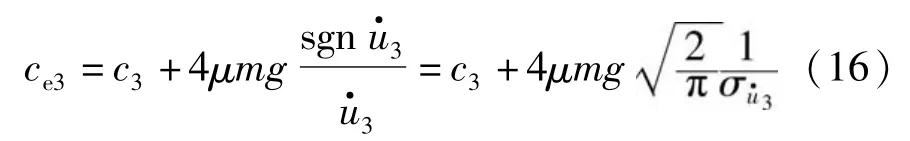
同理可得：

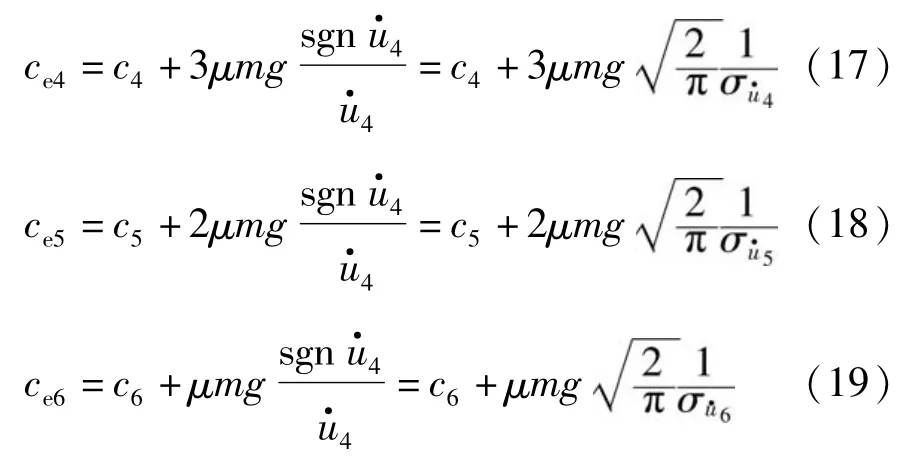
由以上内容可得六层集装箱结构第i层等效阻尼比：

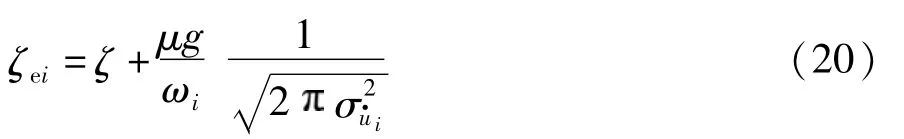
式中：ζ为钢结构阻尼比，可按照文献［21］取值；ωi为第i层结构的自振频率.

1.4 速度均方差公式推导

1.4.1 运动方程简化

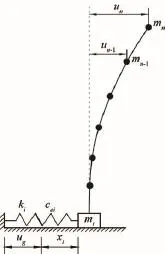
图2 多层隔震集装箱结构等代体系Fig.2 Sstructure equivalentsystem ofmultilayer isolated container

对于图2所示结构，在相对坐标系下，结构运动方程分为两部分：第一部分是上部质点弹性相对振动，第二部分是质点i与上部结构的共同振动，运动方程为：

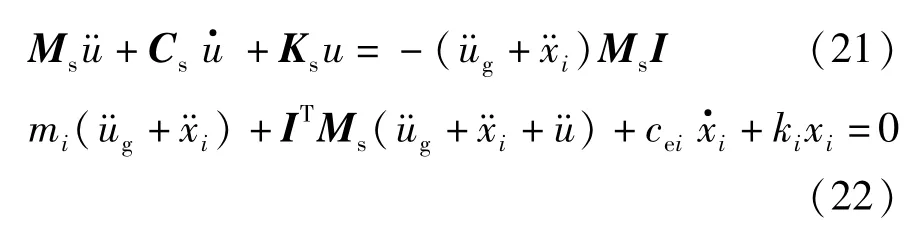
对于式（22），重新整理之后如式（23）所示.

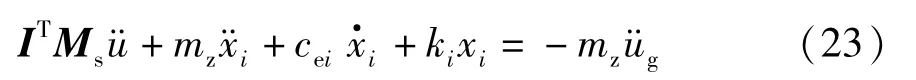
式中，mz为第i层及以上各层结构质量之和.式（23）第一项表示i层以上所有质点相对于i层结构的惯性力，如式（24）所示.

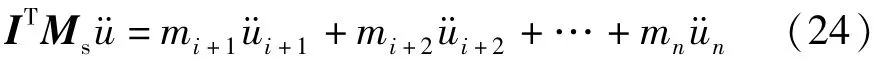
由于在图2所示的结构体系中，有ui≪xi，mi≪mz，所以可将式（24）所示项去掉，由式（23）可得到近似运动方程：

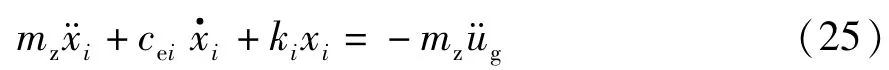
由式（21）和式（25）可知，体系被分解为上部质点弹性相对振动以及i层及以上整体结构相对地面的单质点滑动两种情况.

1.4.2 求解速度均方差

对于图2所示结构，由式（25）可得：

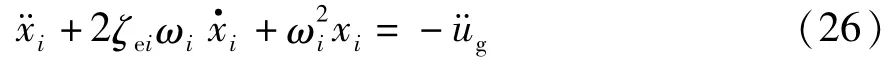
由文献［22-23］可知，当白噪声谱密度常数S0= 55.44 cm2/s3时，可以用白噪声模拟地震地面加速度.因此，地震加速度u¨g可表达为：

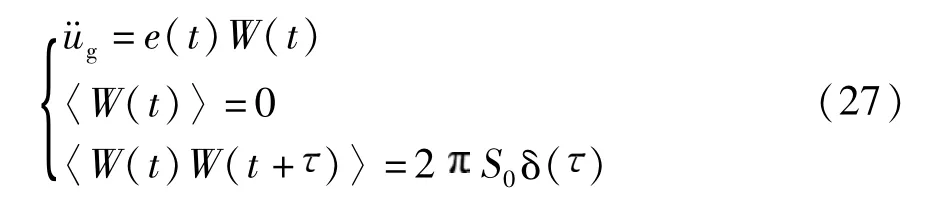
式中：e（t）为包络函数；W（t）为稳态白噪声过程；〈·〉为总体均值；S0为白噪声谱密度常数；δ（）为狄拉克函数.

由文献［24］可知，由相关函数与谱密度的关系，并根据Fourier变换公式，可得平稳白噪声的相关函数表达式：

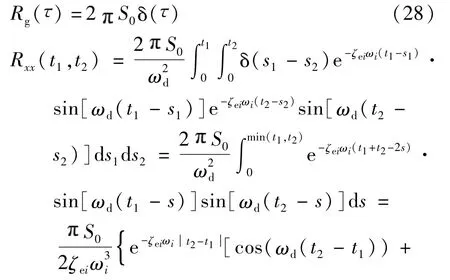
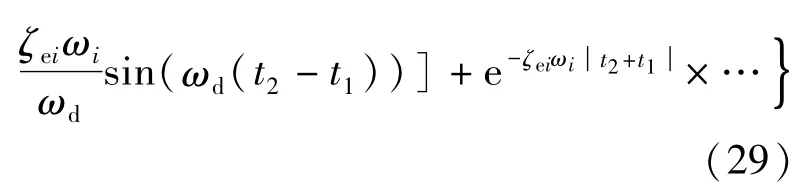
式中：ωd可表示为，其中ω0为固有圆频率，

当t→∞时，式（29）可以表示为

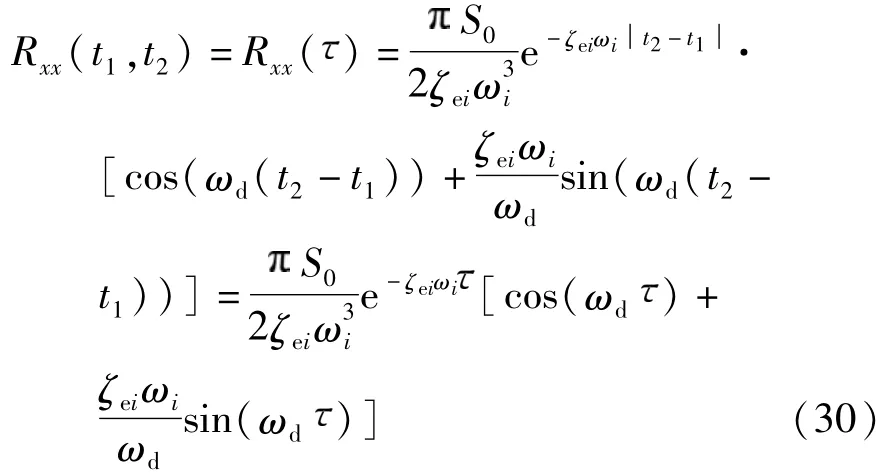
从而可以得到：

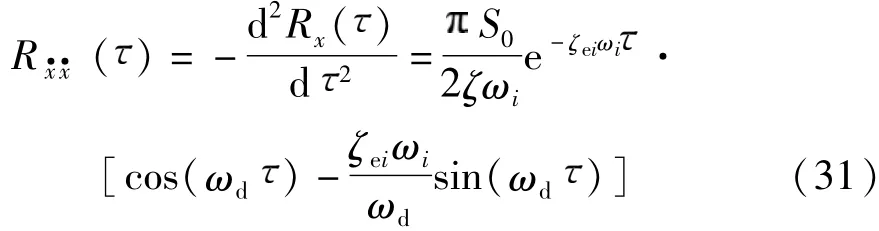
所以处于稳态阶段的速度均方差表达式为

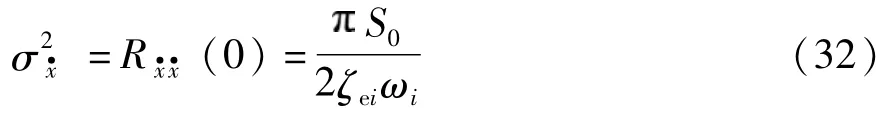
由式（20）和式（32）可得：

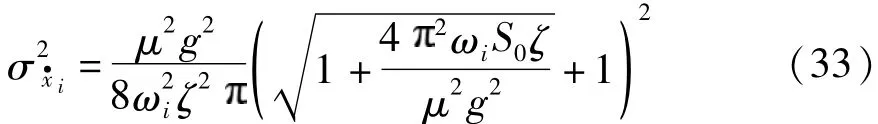
将式（31）代入式（18），得到各层等效阻尼比公式：

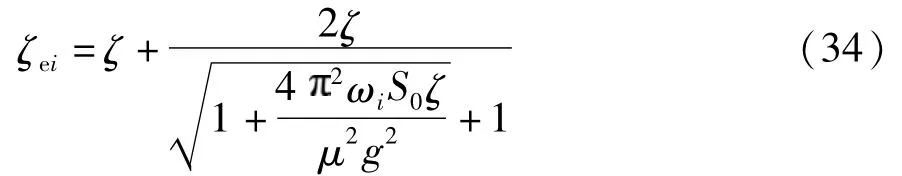
1.5 六层滑移隔震结构算例

某住宅为一幢六层层层滑移隔震集装箱结构，集装箱采用20 ft标准集装箱，结构阻尼比取0.05，每层质量为2230 kg，层与层之间摩擦系数取0.15，集装箱刚度由文献［11］可取70 kN/mm，白噪声谱密度常数S0取55.44 cm2/s3.

将以上参数代入式（34），可以求得第二层到第六层的等效阻尼比分别为0.090、0.089、0.088、0.087、0.084.

2 有限元模拟

2.1 六层集装箱结构有限元模型

利用非线性软件Abaqus［25］建立六层集装箱结构，对模型尺寸的选用，参考了文献［26］中的标准集装箱.六层集装箱有限元模型及其网格划分如图3所示.

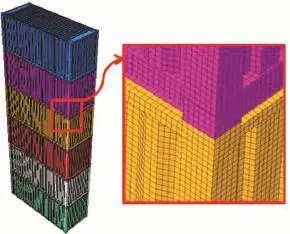
图3 六层集装箱抗震分析模型Fig.3 Seismic analysismodel of Six-layer container

阻尼采用瑞雷阻尼，对于非隔震结构的阻尼α和β可分别取1.1339和0.001688，对于滑移隔震结构的阻尼α和β可分别取1.8369和0.002735［14］.

2.2 结构弹塑性时程分析

2.2.1 结构各层最大位移

按照文献［21］中规定，文中选用3条地震波，不同地震作用下结构各层最大位移包络图如图4所示.

从图4中可以看到，该结构刚度沿竖向分布均匀，没有薄弱楼层，而且滑移隔震体系能够有效地减小结构各层最大位移.

对于集装箱结构，如果采用钢结构规范中的阻尼比，则利用等效阻尼比公式计算得到的结果较大，所以各层最大位移是减小的.

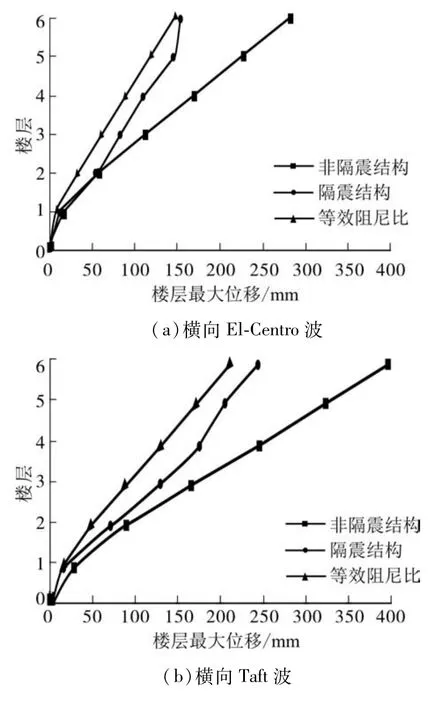
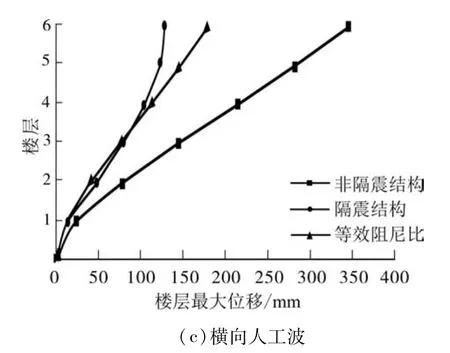
图4 结构各层最大位移Fig.4 Maximum displacement of each structural layers

2.2.2 结构各层位移角

因为集装箱底板以槽钢为底梁，上面铺置木板或混凝土板，所以在分析多层集装箱结构时，由于箱体之间采用集装箱角件锁连接，每层箱底与下一层箱顶可认为平面内刚度无限大，对于多层集装箱结构层间位移角可以定义为层间最大位移与层高之比.

不同地震波作用下结构各层最大层间位移角如图5所示.由图5可以看出，3种地震波作用下，隔震结构和采用等效阻尼比的非隔震结构的最大层间位移角远小于采用规范阻尼比的非隔震结构的最大层间位移角.同时，从图中也可以看出，采用规范阻尼比的非隔震结构和等效阻尼比的非隔震结构最大层间位移角主要发生在结构中上部，而隔震结构最大层间位移发生在第二层.3种结构在3种地震波作用下的结构最大层间位移角如表1所示.

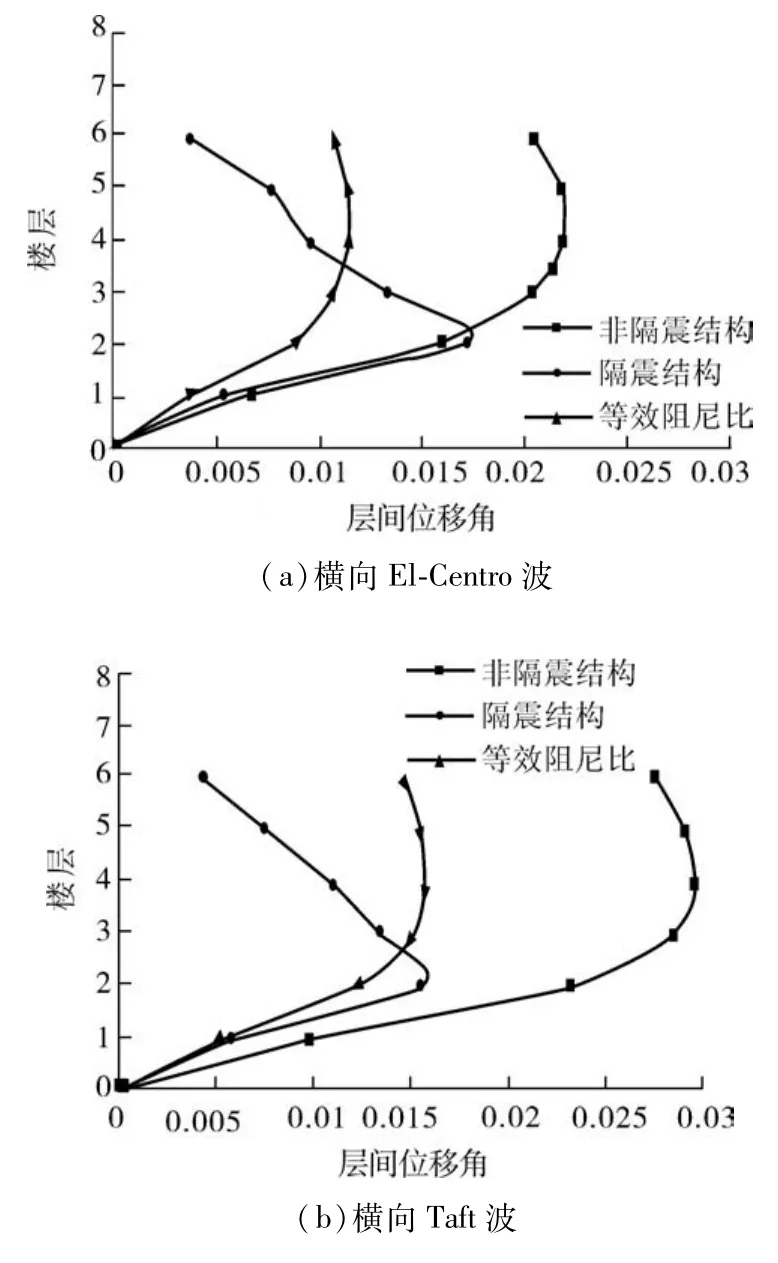
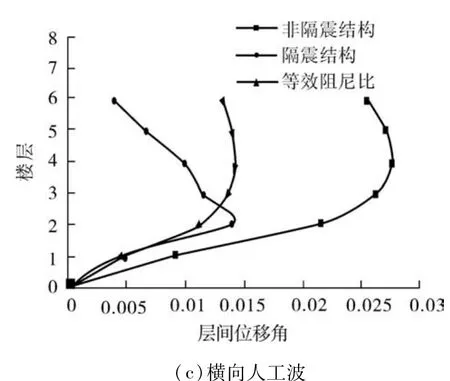
图5 结构各层位移角Fig.5 Displacement angle of each structural layers

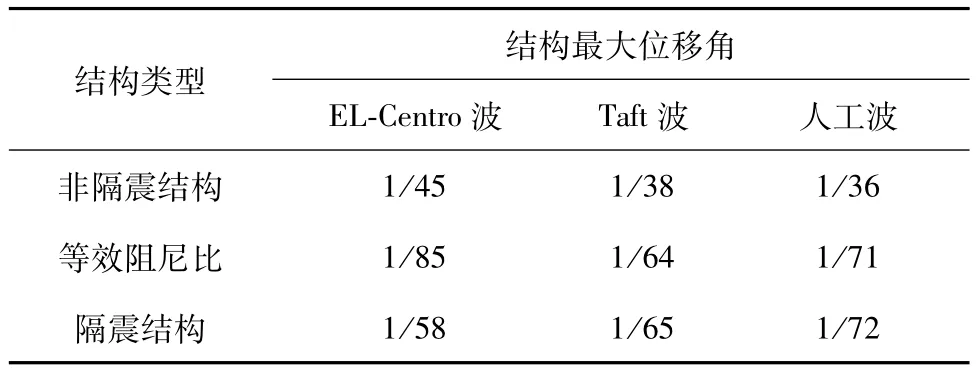
表1 不同地震波下结构的最大位移角Table.1 Structuralmaximum displacement angle under different seismic waves

由文献［21］可知，对于多、高层钢结构，弹塑性层间位移角限制为1/50.由表1可以看出：对于非隔震集装箱结构横向最大层间位移角，在3种地震波作用下都超过规范规定值1/50，最大为人工波作用下的1/36，不能满足要求.采用等效阻尼比的非隔震集装箱结构在3种地震波作用下，横向最大层间位移角均有所减小，且均小于规范规定限值1/50.同时，对于隔震结构，横向层间位移角也均小于规范规定值.这说明滑移隔震体系对集装箱结构抵抗地震作用是有效的.

通过对比采用等效阻尼比的非隔震结构和层层滑移隔震结构的计算结果，可以发现，两种集装箱结构的最大层间位移角在Taft波和人工波作用下几乎相等，说明文中推导得出的等效阻尼比计算公式可以用于简化计算层层滑移隔震结构.

2.2.3 结构各层滑移量

3种地震作用下层层滑移隔震结构各层滑移量随时间的变化如图6所示.从图6中可以看出，结构各层滑移量各不相同.总体来看，结构上部滑移量较下部大，并且Taft波下结构滑移量最大，这说明地震波的频谱特性会明显影响结构的动力反应.由图6（b）可知，结构第六层在3种地震波下最大滑移量可达到30mm.所以在设置集装箱隔震体系时，角件上滑动孔长度设置到35mm就可满足要求.

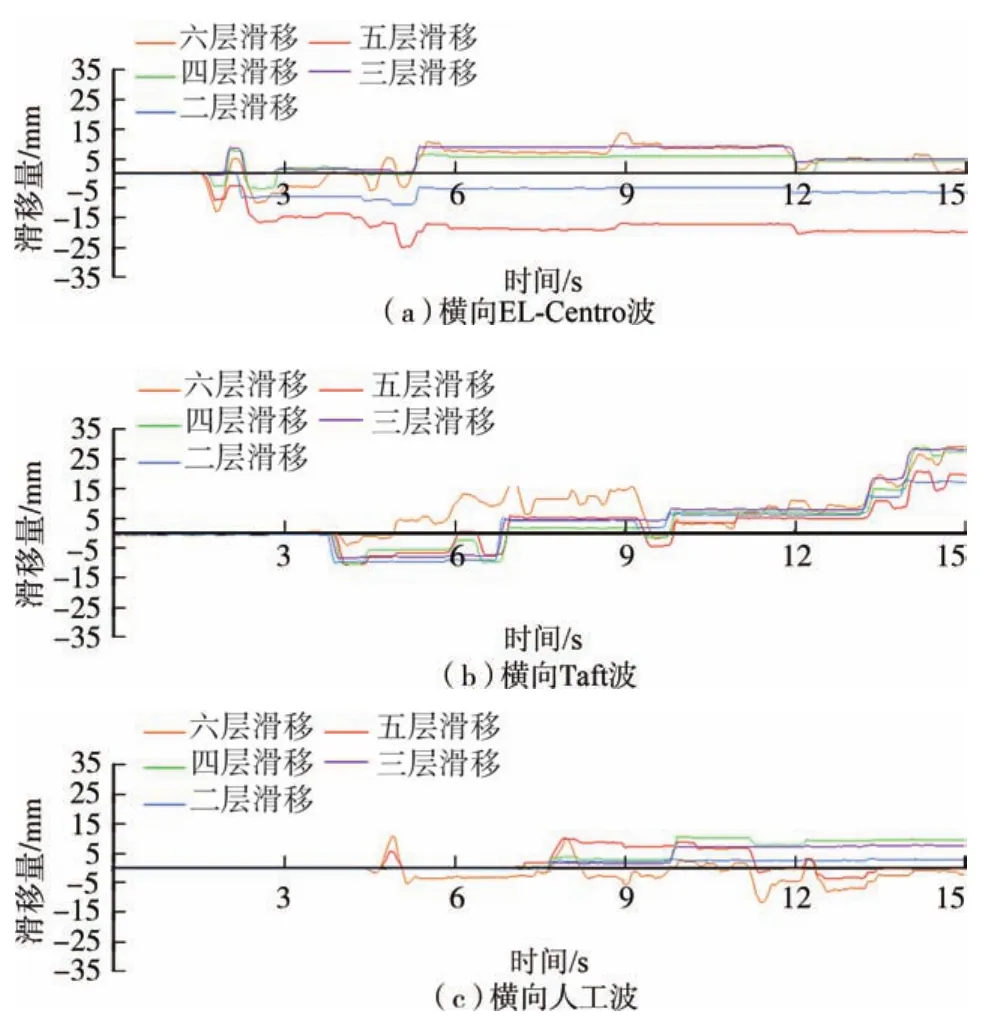
图6 结构各层滑移量Fig.6 Slip of each structural layers

3 结论

文中针对六层集装箱结构提出了一种层层滑移隔震方法；推导了摩擦系数和阻尼比之间的关系，得到了各层等效阻尼比；并以某六层层层滑移隔振集装箱结构为例，对采用规范阻尼比的非隔震结构、采用等效阻尼比的非隔震结构和隔震结构分别在不同地震波作用下的动力反应进行了弹塑性时程研究，得出以下主要结论：

（1）滑移隔震体系能有效减小结构各层最大位移.

（2）隔震结构和采用等效阻尼比的非隔震结构的最大层间位移角远小于采用规范阻尼比的非隔震结构的最大层间位移角；采用规范阻尼比的非隔震结构和等效阻尼比的非隔震结构最大层间位移角主要发生在结构中上部，隔震结构最大层间位移发生在第二层.

（3）地震波的频谱特性会明显影响层层滑移隔振结构的动力反应，Taft波下结构滑移量最大.

［1］ Kotnik J.Container architecture［M］.Barcelona：Leading International Key Services Barcelona，2013.

［2］ Slawik H，Bergmann J.Container atlas：a practical guide to container architecture［M］.Berlin：Die Gestalten Verlag，2010.

［3］ Smith J D.Shipping containers as building component［D］.Brighton：Departmentof the Built Environment，University of Brighton，2005.

［4］ 柏庭卫，顾大庆.香港集装箱建筑［M］.北京：中国建筑工业出版社，2004.

［5］ 王蔚，魏春雨.集装箱建筑的模块化设计与低碳模式［J］.建筑学报，2011（S1）：130-135. Wang Wei，Wei Chun-yu.The modular design and the low-carbon model of the container building［J］.Architectural Journal，2011（S1）：130-135.

［6］ 王蔚，魏春雨.LOT-EK的集装箱建筑设计之路［J］.工业建筑，2012，42（S1）：37-40. Wang Wei，Wei Chun-yu.Road of design of lot-ek container architectures［J］.Industrial Construction，2012，42（S1）：37-40.

［7］ 纪尚志，孙维琛.集装箱建筑的应用与探索——从青岛积米崖渔人码头概念规划说起［J］.青岛理工大学学报，2009（1）：35-39. Ji Shang-zhi，Sun Wei-chen.The application and exploration of container construction：a discussion about the planning concept ofqingdao jimiya fisherman's wharf［J］. Journal of Qingdao Technological University，2009（1）：35-39.

［8］ Aguiar De Souza V，Suzuki K.Experimental and numerical analysis of container stack dynamics using a scaled model test［J］.Ocean Engineering，2012，39：24-42.

［9］ Børvik T，Hanssen A G.On the ballistic and blast load response of a 20 ft ISO container protected with aluminium panels filled with a localmass（Phase I）：design of protective system［J］.Engineering Structures，2008，30（6）：1605-1620.

［10］ Børvik T，Burbach A.On the ballistic and blast load response of a 20 ft ISO container protected with aluminium panels filled with a localmass（Phase II）：validation of protective system［J］.Engineering Structures，2008，30（6）：1621-1631.

［11］ Giriunas K，Sezen H.Evaluation，modeling，and analysis of shipping container building structures［J］.Engineering Structures，2012，43：48-57.

［12］ 查晓雄.轻钢活动房计算理论——静动力、优化、性能化防火、集装箱改造房［M］.北京：科学出版社，2011.

［13］ 查晓雄，左洋.多体集装箱房屋纵向刚度的理论和有限元研究［J］.建筑钢结构进展，2014（4）：24-28. Zha Xiao-xiong，Zuo Yang.Study on theory and finite element analysis of longitudinal stiffness ofmulti-body container building［J］.Progress in Steel Building Structures，2014（4）：24-28.

［14］ 左洋，查晓雄，开洞集装箱房屋结构纵向刚度分析［J］.天津大学学报：自然科学与工程技术版，2015，48（2）：167-176. Zuo Yang，Zha Xiao-xiong.Analysis of longitudinal stiffness of container building structurewith holes［J］.Journal of Tianjin University：Science and Technology，2015，48（2）：167-176.

［15］ Zha Xiao-xiong，Zuo Yang.Study on the optimal design of themembers of contaniner building with buildingmaterials I：side board optimization［J］.Advanced Materials Research，2013，859：270-273.

［16］ Zha Xiao-xiong，Zuo Yang.Study on the optimal design of themembers of contaniner building with buildingmaterials II：joint and corner column optimization［J］.Advanced Materials Research，2013，859：266-269.

［17］ 查晓雄，刘乐，左洋.集装箱房屋在高温下的力学性能研究［C］∥第五届全国钢结构工程技术交流会论文集.北京：施工技术杂志社，2014：315-320.

［18］ 查晓雄，王璐璐，左洋.集装箱房屋模块化研究Ⅰ：竖向荷载作用下［C］∥第五届全国钢结构工程技术交流会论文集.北京：施工技术杂志社，2014：321-324.

［19］ 查晓雄，王璐璐，左洋.集装箱房屋模块化研究Ⅱ：水平荷载作用下［C］∥第五届全国钢结构工程技术交流会论文集.北京：施工技术杂志社，2014：325-328.

［20］ Gewei Z，Basu B.A study on friction-tuned mass damper：harmonic solution and statistical linearization［J］. Journal of Vibration and Control，2011，17（5）：721-731.

［21］ GB50011—2010，建筑抗震设计规范［S］.

［22］ Bycroft N G.White noise representation of earthquakes［J］.ASCE Journal of the Engineering Mechanics Division，1960，86（2）：1-16.

［23］ Housner W G.Properties of strong ground motion earthquakes［J］.Bulletin of the Seismological Society of A-merica，1955，45（3）：197-218.

［24］ 欧进萍，王光远.结构随机振动［M］.北京：高等教育出版社，1998.

［25］ 庄茁，由小川.基于ABAQUS的有限元分析和应用［M］.北京：清华大学出版社，2009.

［26］ ISO/TC 104.ISO 668：2013 Series 1 freight containersclassification，dimensions and ratings［S］.

Analysis of M echanical Properties of Container Structure Under Earthquake Action

Zha Xiao-xiong Zuo Yang Liu Le Wang Xin-jie
（Shenzhen Graduate School，Harbin Institute of Technology，Shenzhen 518055，Guangdong，China）

Aiming at the widely-used multilayer container buildings，a new sliding isolation system is proposed on the basis of the friction energy dissipation between containers.Firstly，a sliding isolation structure model is constructed，and a relationship between the equivalent damping ratio and the friction coefficient of each layer of layerupon-layer sliding isolation structure is derived through the random vibration theory.Then，a six-layer container model are constructed on the basis of the nonlinear finite element software Abaqus，and the elasto-plastic nonlinear time history of dynamic response for strong earthquake is investigated on an isolated structure，a non-isolated structure of ordinary damping ratio and a non-isolated structure of equivalent damping ratio.Finally，the relative structure indexes，such as the top displacement，the angular displacementbetween structural layers and the slip between structural layers，are analyzed.The results show that（1）the proposed sliding isolation system can reduce themaximum displacement of each structural layer effectively；（2）the isolated structure and the non-isolated structure with equivalent damping ratio havemuch smallermaximum angular displacement between structural layers than the non-isolated structure with specification damping ratio does；and（3）the spectral characteristics of seismic waves can affect the dynamic response of layer-upon-layer sliding isolation structures significantly.

multilayer container building；earthquake action；isolation system；sliding；equivalent damping ratio；mechanical property

TU392.5

10.3969/j.issn.1000-565X.2015.07.013

1000-565X（2015）07-0092-08

2014-09-26

国家科技支撑计划项目（SQ2011GX07E03036）

Foundation item：Supported by the National Key Technology Research and Development Program of the Ministry of Science and Technology of China（SQ2011GX07E03036）

查晓雄（1968-），男，博士，教授，主要从事钢结构非线性力学分析、建筑钢结构抗火、抗震等研究.E-mail：zhaxx@hit.edu.cn