钢板-混凝土组合板在横向集中荷载作用下的破坏模式分析*

吴丽丽 刘艳 姜宇鹏 张栋栋

（中国矿业大学（北京）深部岩土力学与地下工程国家重点实验室∥力学与建筑工程学院，北京 100083）

钢板-混凝土组合板在横向集中荷载作用下的破坏模式分析*

吴丽丽 刘艳 姜宇鹏 张栋栋

（中国矿业大学（北京）深部岩土力学与地下工程国家重点实验室∥力学与建筑工程学院，北京 100083）

采用ANSYS有限元与试验相结合的方法，研究了板件截面抗弯承载力与抗剪承载力随剪跨比变化的趋势，分析了在跨中单点(两点对称)加载下剪跨比对板件破坏模式的影响规律.结果表明：钢板剥离破坏仅发生在抗剪连接件不完全剪力连接时的板件；在跨中单点(两点对称)加载下，剪跨比小于7.5(7)时，截面抗弯承载力较抗剪承载力充足，试件发生剪切破坏；剪跨比在7.5(7)与10(9)之间时，截面抗弯与抗剪承载力均不足，试件发生弯剪破坏；剪跨比大于10(9)时，截面抗弯承载力较抗剪承载力不足，试件发生弯曲破坏.

钢板-混凝土组合板；剪跨比；抗弯承载力；抗剪承载力；受弯性能；破坏模式

钢板-混凝土组合板近几年来在建筑及桥梁领域逐渐受到关注.它构造简洁、施工快捷、无支模工序、易于满足桥梁的平面形状要求，抗裂性能及抗震性能较好，具有广阔的应用前景.

国内外众多学者对各种形式的钢板-混凝土组合构件的抗弯性能进行了广泛的研究.20世纪50年代，Casillas等［1］采用钢板代替钢筋混凝土板中的钢筋，采用栓钉作为抗剪连接件来连接钢板与混凝土，并对此种形式的构件进行了详细的研究，实验表明，钢板与混凝土之间的微小滑移不影响两者的共同工作，试验中部分板件由于栓钉连接件受到的荷载过大产生较大的滑移而破坏.

聂建国等［2-4］对开口型与闭口型压型钢板（轻骨料）混凝土组合板的受力性能、动力性能、疲劳性能等进行了研究，并分析了钢-混凝土组合板弹性局部和整体的剪切屈曲［5-6］，其相关结论为工程中组合板的设计提供了依据和参考.

左莹、杨悦等［7-8］通过对不同类型的钢板-混凝土组合板的试验研究，分析了板件的受力性能和破坏形态的影响因素，并提出一些实用的理论计算公式.

马晓伟和胡红松等［9-10］对双钢板-混凝土剪力墙的变形能力进行了分析，并提出可用于双钢板-混凝土剪力墙压弯承载力设计的数值模型及简化计算公式.

此外，在钢板夹心混凝土组合结构方面，Uy等［11-13］对钢板夹心混凝土组合结构进行了试验研究.

国内外学者的研究表明，不同截面及受力状态下，组合板的破坏可能有4种主要模式：弯曲破坏、纵向剪切破坏、垂直剪切破坏和冲切破坏.

笔者所在课题组先后进行了两批试验，试验观测到钢板-混凝土组合板在受弯状态下的破坏模式主要有：钢板剥离破坏（加载初期，栓钉滑移量较小，近似服从线性变化，加载中后期，随着荷载的增加，滑移量迅速发展，曲线斜率不断变小，直到栓钉由于滑移过大而被剪断，钢板剥离造成板件破坏）；弯剪破坏（弯曲破坏与剪切破坏的混合破坏，即在构件产生弯曲破坏特征后由于抗剪承载力不足，导致构件最终破坏）；剪切破坏（由于抗剪承载力不足，导致板件出现斜裂缝而破坏）；弯曲破坏（由于抗弯承载力不足，导致板顶加载处混凝土被压溃，跨中板底钢板受拉屈服，导致试件卸载而破坏）.

文中采用ANSYS有限元对简支钢板-混凝土组合板进行参数分析，通过变化试件的剪跨比，研究组合板截面抗弯承载力与抗剪承载力随剪跨比变化的趋势；通过分析板件的破坏模式，分别得出跨中单点加载及两点对称加载下，剪跨比对组合板破坏模式的影响规律，提出简支组合板发生各种破坏形态的剪跨比阈值，并与试验结果进行对比分析.

1 ANSYS有限元模型及数值计算

采用ANSYS有限元对简支钢板-混凝土组合板进行非线性数值模拟.组合板数值计算基本参数如表1和表2所示，模拟中固定组合板中混凝土厚度为100mm，钢板厚度为6mm，栓钉均按完全剪力连接设置，通过变化试件跨度的方式变化剪跨比（板件剪跨比等于加载点至支座处的距离除以板件厚度），进行对比分析.

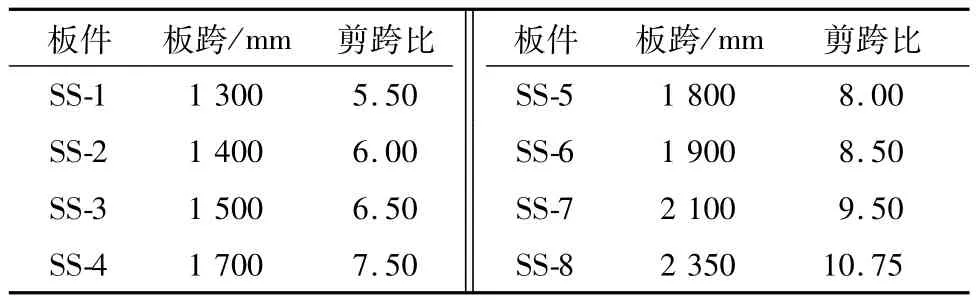
表1 单点加载下的组合板数值计算基本参数Table 1 Basic parameters of composite slabs numerical calculation under single loading points

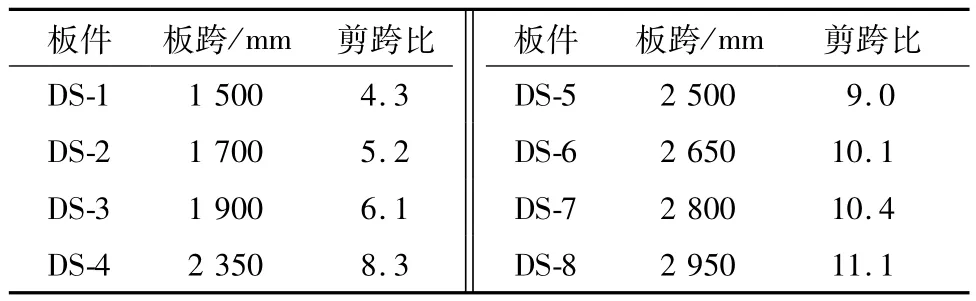
表2 两点加载下的组合板数值计算基本参数Table 2 Basic parameters of composite slabs numerical calculation under two loading points

1.1 ANSYS有限元模型

1.1.1 材料本构关系

混凝土的受压本构关系采用Hongnestad［14］曲线，受拉本构关系采用简化受拉模型曲线，本构关系曲线如图1所示.

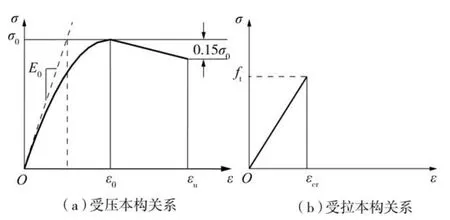
图1 混凝土本构关系Fig.1 Constitutive relationship of concrete

钢材采用Q235钢，钢板抗拉强度取自材性试验结果，钢材的弹性模量Es=206 GPa.钢板本构关系采用理想弹塑性模型，如图2所示.

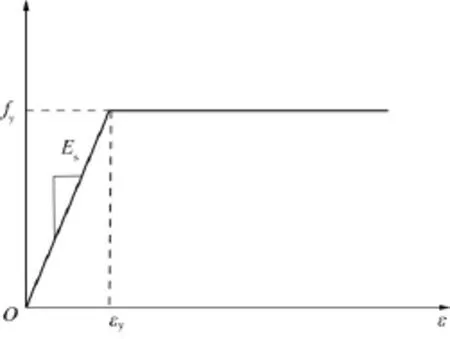
图2 钢材本构关系Fig.2 Constitutive relationship of steel

为了考虑抗剪连接件滑移产生的影响，在定义栓钉抗剪连接件本构关系时，采用Ollgaard［15］在20世纪70年代提出的栓钉剪力-滑移模型，如图3所示.

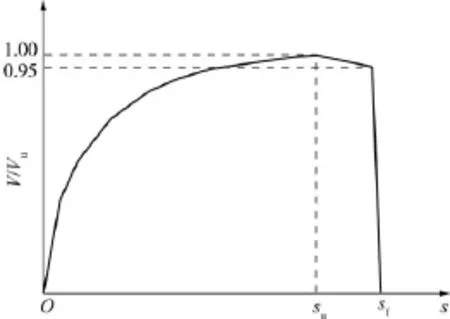
图3 栓钉剪力-滑移曲线Fig.3 Shear-slip curve of stud

1.1.2 有限元加载模型

钢板-混凝土组合板有限元加载模型如图4所示，混凝土、钢板、栓钉分别采用SOLID 65、SOLID 45与COMBIN 39弹簧单元模拟，弹簧单元连接底部的钢板单元及上部的混凝土单元，在支座处及加载处设置弹性垫块，以避免加载过程中由于应力集中造成试件破坏.采用力控制收敛准则，在垫板上的节点设置竖向位移约束，采用位移加载的方式.有限元求解方法使用非线性迭代法，将荷载分解为一系列增量，在每一增量步求解结束后，调节刚度矩阵以适应非线性响应.

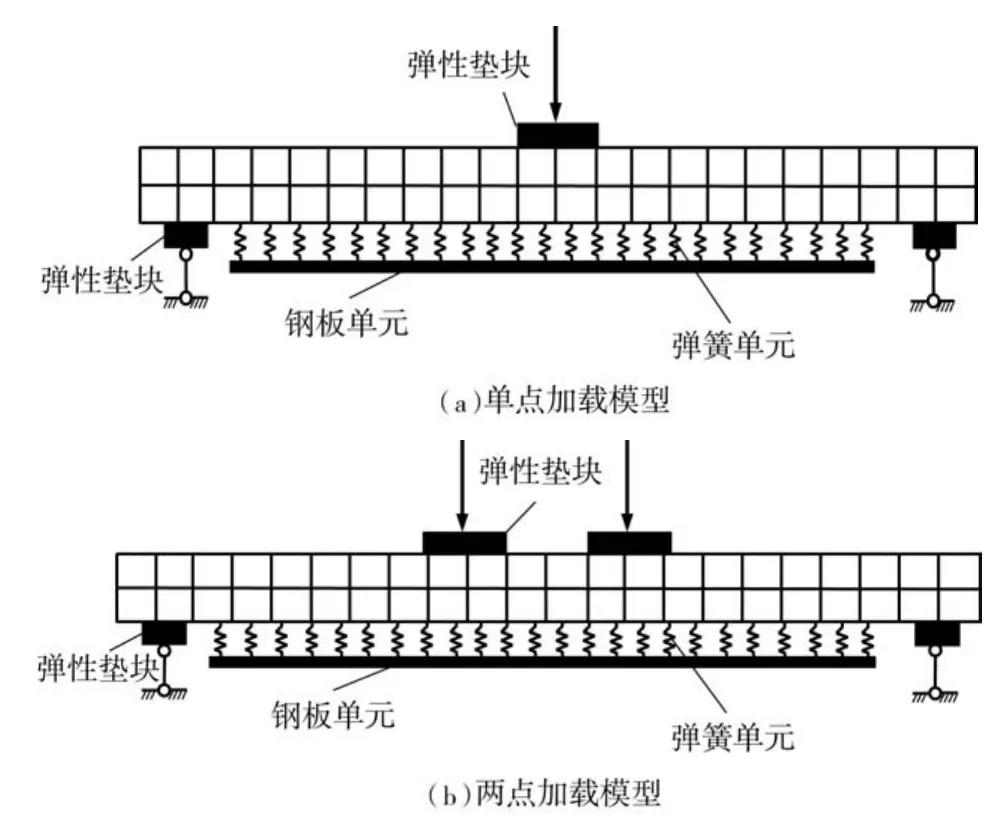
图4有限元加载模型Fig.4 Finite elementmodel of load

1.2 有限元计算结果及分析

1.2.1 组合板数值模拟结果

通过数值模拟，在两种加载情况下，各板件处在极限状态时剪跨段的剪力V和跨中最大弯矩M如表3和表4所示.

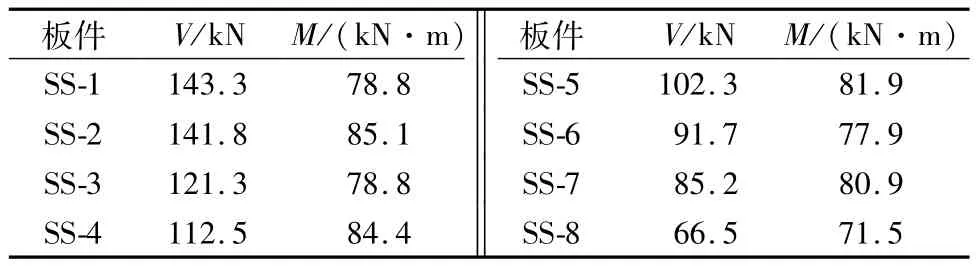
表3 单点加载模式下各板件在极限状态时剪跨段的剪力和跨中最大弯矩Table 3 The shear and maximum bendingmoment of each slab in the limit state when the slab is cut under the single point of loading.

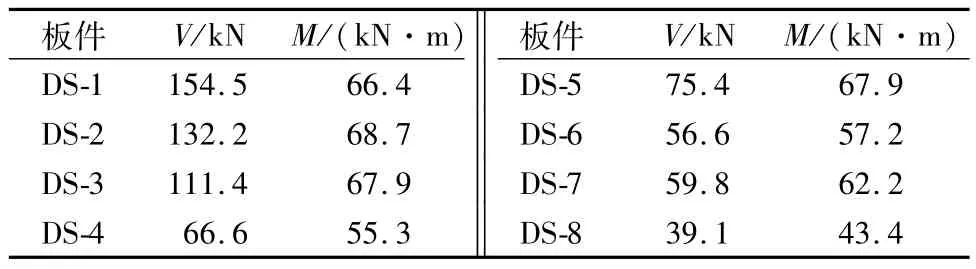
表4 两点加载模式下各板件在极限状态时剪跨段的剪力和跨中最大弯矩Table 4 The shear and maximum bendingmoment of each slab in the limit state when the slab is cut under the two point of loading

1.2.2 组合板数值模拟结果分析

由前期试验结果可知，钢板-混凝土组合板在受弯状态下的受力性能类似钢筋混凝土构件，将组合板底部钢板看作钢筋，参考钢筋混凝土受弯构件正截面承载力计算公式，采用塑性设计理论研究组合板截面极限弯矩.计算中忽略混凝土的抗拉能力，钢板-混凝土组合板应力采用等效截面应力分布.则混凝土受压区高度为

组合板截面极限弯矩为

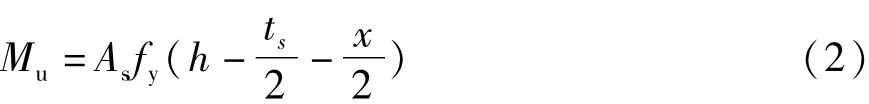
式中：As为钢板截面面积；h为组合板高度；ts为钢板厚度；fy为钢板的屈服强度；为混凝土受压区等效矩形应力图系数；fc为混凝土轴心抗压强度，fc=0.76 fcu；x为混凝土受压区高度.

总而言之,预见性护理时妊高症患者的可靠护理措施,对病情发展有预测性,能够提前的针对性护理,减少母婴并发症,保障其安全,临床中应该进行推广使用。

由于目前尚无可依据的组合板截面抗剪承载力计算方法或公式，且其抗剪承载性能主要依靠混凝土板，所以暂且参考无腹筋钢筋混凝土板斜截面抗剪承载力计算公式来计算钢板-混凝土组合板斜截面抗剪承载力.则组合板截面抗剪承载力为

式中：βh为截面高度影响系数；b为组合板有效宽度；ft为混凝土轴心抗拉强度设计值；h0为组合板有效高度，当h0＜800mm时，取h0=800mm.

将表3和表4中的数值模拟结果V和M分别除以式（3）和式（2）做无量纲化处理，得出钢板-混凝土组合板在单点和两点对称加载下，板件截面抗弯承载力与抗剪承载力的无纲量化结果，如图5所示，图中纵坐标ρ为极限状态下V/Vu、M/Mu，横坐标为剪跨比.

从图5可以看出，在跨中单点和两点对称加载下，随着剪跨比的增大，各板件在极限状态时跨中最大弯矩变化幅度不大，且M/Mu总是大于1，这是因为Mu是将钢板假想成钢筋，参考钢筋混凝土受弯构件正截面承载力公式计算的结果，而有限元计算结果M是将钢板和混凝土板通过弹簧单元模拟栓钉的连接作用，考虑了两种材料的组合效应，考虑组合效应的有限元计算值必然会大于钢筋混凝土受弯构件的计算结果.而随着剪跨比的增大，剪力值下降幅度较大，参考无腹筋钢筋混凝土板在集中荷载下的抗剪承载力公式，可知随着剪跨比的增大，其抗剪承载力逐渐减小，正好与计算的结果吻合.

此外，由图5可见，在跨中单点（两点对称）加载下，当λ＜7.5（λ＜7）时，，截面抗剪承载力不足，抗弯承载力较抗剪承载力充足，试件发生剪切破坏；当7.5＜λ＜10（7＜λ＜9）时，截面抗剪承载力不足，抗弯承载力较抗剪承载力不足，试件发生弯剪破坏；当λ＞10（λ＞9）时，截面抗剪承载力充足，抗弯承载力不足，试件发生弯曲破坏.

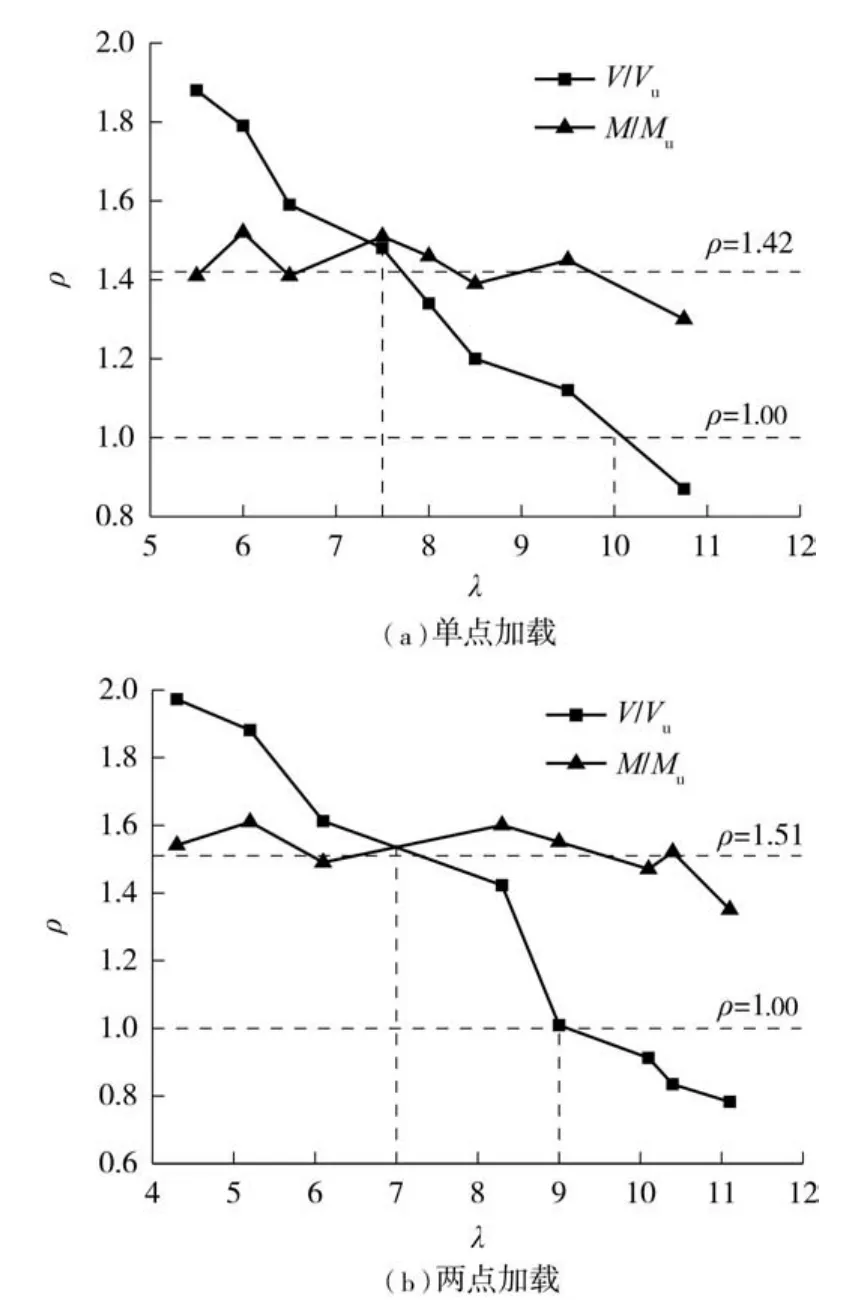
图5 板件截面的无量纲化抗弯、抗剪承载力Fig.5 Flexural and shear dimensionless quantitative bearing capacity of slab sections

2 试验设计及加载方式

笔者所在课题组先后对两批钢板-混凝土组合板抗弯性能进行了研究.共完成5组（共11块板，其中S1J2板件同时用于4种参数的对比组中）静力加载试验，各组分别变化栓钉间距J、组合板厚度h、钢板厚度ts、混凝土厚度bc、组合板长宽比a/b等参数.板件中混凝土设计强度等级为C40，材性试验测得混凝土立方体抗压强度平均值为45.5MPa.钢材为Q235钢，材性试验测得6、8和10mm钢板的屈服强度分别为412.49、309.77、300.07MPa，极限强度分别为592.60、471.78、457.09MPa.

试件底面钢板采用φ10栓钉剪力连接件与混凝土连接，栓钉在钢板面均匀布置并施焊，板件规格尺寸见表5，板件测点布置图如图6所示，板件加工、加载示意图如图7所示.

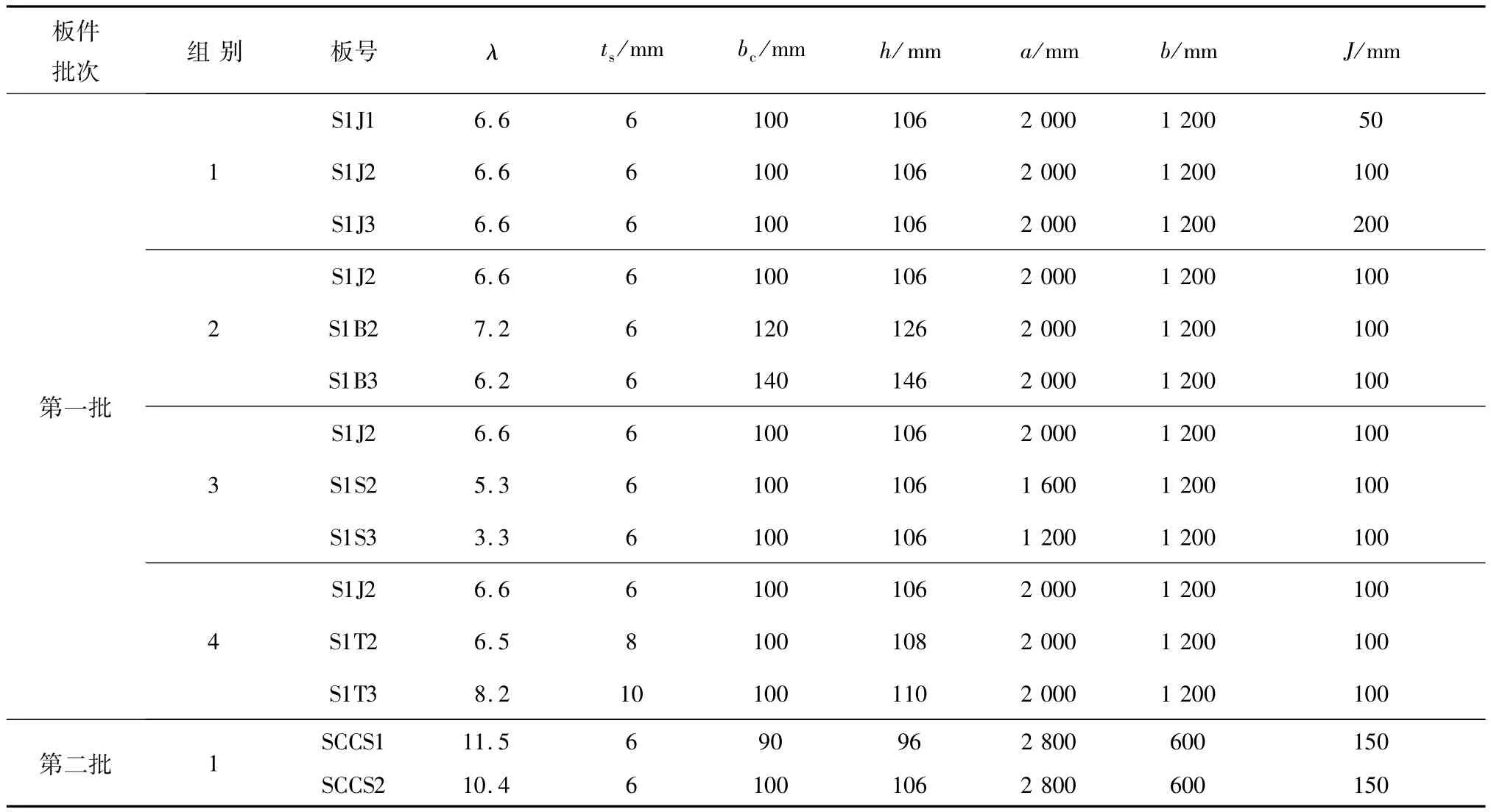
表5 组合板试件规格尺寸Table 5 Parameters of composite slabs specimens

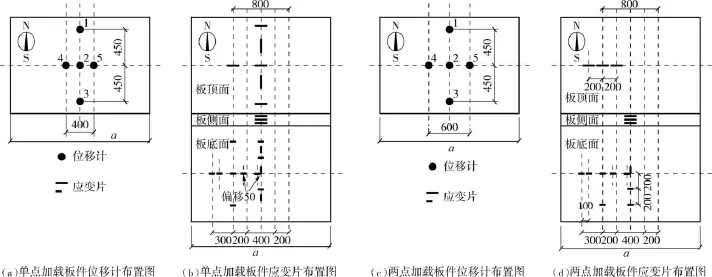
图6 板件测点布置图（单位：mm）Fig.6 Measuring points arrangement of Slabs（Unit：mm）

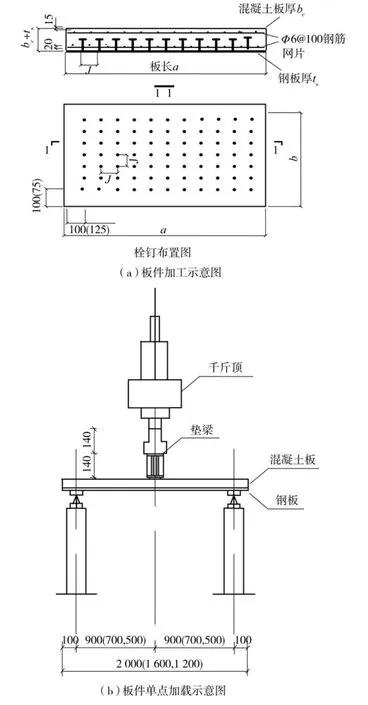
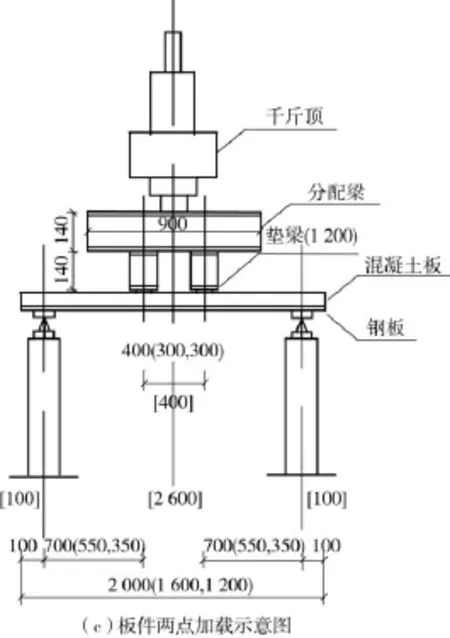
图7 板件加工、加载示意图（单位：mm）Fig.7 Slabs processing and loading diagram（Unit：mm）

3 有限元与试验验证

为确保数值模型的合理性，以试件SCCS1进行两点加载数值模拟，并将数值计算的结果与试验实测结果进行对比.钢板-混凝土组合板的数值模拟结果和试验实测得到的荷载-挠度曲线如图8所示.

由图8可见，组合板有限元模拟得到的荷载-挠度曲线与试验实测结果基本吻合.

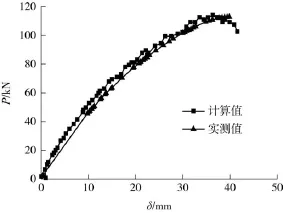
图8 钢板-混凝土组合板荷载-挠度曲线Fig.8 Load-deflection curves of steel plate-concrete composite slabs

钢板-混凝土组合板SCCS1两点加载有限元模拟结果和试验中试件的破坏情况如图9所示.

图9 板件SCCS1数值模拟结果与试验结果对比Fig.9 Compare of results between numerical simulation and experiment of Slabs SCCS1

由图9（a）可见，在加载区混凝土应变达到了4.4×10-3，表示此处混凝土被压溃；由图9（b）可见，构件达到极限承载力时，加载处附近混凝土表面大量被掀起，混凝土被压溃，构件出现大规模卸载并破坏，与有限元结果相符.

由以上结果可见，文中建立的有限元模型可以较好地模拟钢板-混凝土组合板的承载能力和变形性能.

3.2 试验构件破坏模式的验证

根据加载方案，对各试件进行了试验，结果如表6和表7所示.

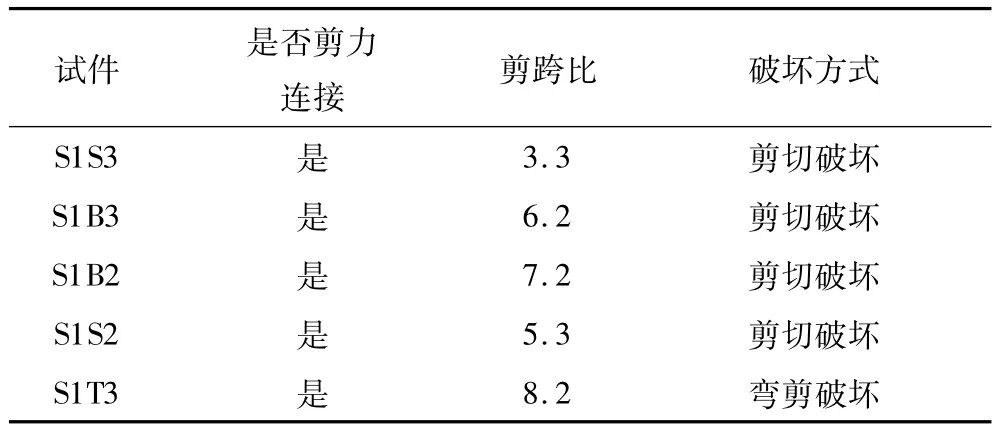
表6跨中单点加载试验结果Table 6 Test results of single point loading of themidspan

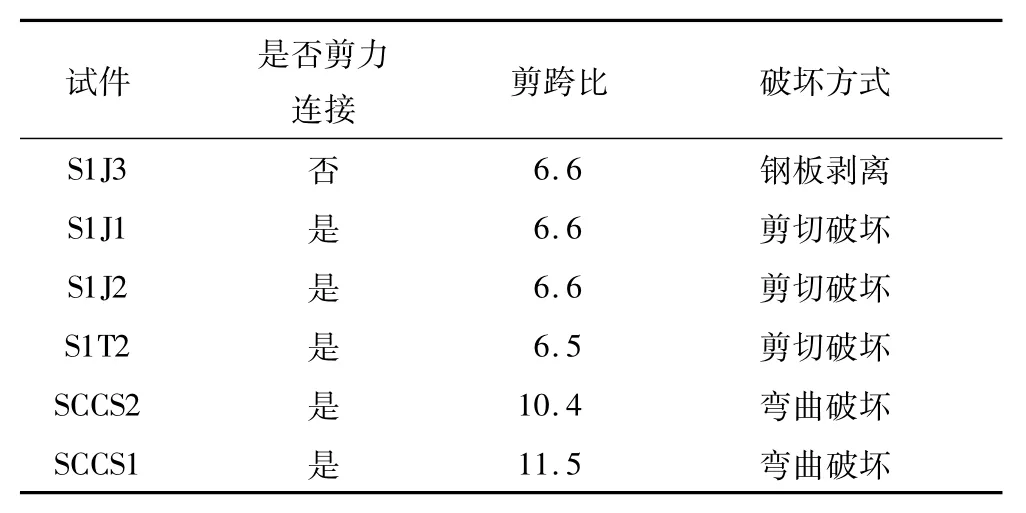
表7 跨中两点加载试验结果Table 7 Test results of two point loading of themidspan

从表6可以看出，在单点加载情况下，试件S1S3、S1B3、S1B2、S1S2的剪跨比均小于7.5，发生剪切破坏；试件S1T3剪跨比介于7.5与10之间，发生弯剪破坏.从表7可以看出，在两点加载情况下，试件S1J1、S1J2、S1T2的剪跨比小于7，发生了剪切破坏；钢板剥离破坏仅发生在抗剪连接件不完全剪力连接时的板件S1J3.本试验中，试件SCCS1、SCCS2的剪跨比大于9，发生了弯曲破坏.通过与前期所有试验结果对比，可知文中提出的单点或两点加载情况下组合板破坏形态的剪跨比阈值结果与前期试验结果吻合良好.

4 结论

通过变化试件的剪跨比，对钢板-混凝土组合板进行了非线性有限元分析，通过对比极限状态下钢板-混凝土组合板截面抗弯、抗剪承载力，分析了简支组合板的破坏模式，得到的主要结论如下：

（1）钢板-混凝土组合板有限元模拟得到的极限承载力及变形性能与试验实测得到的数据基本吻合，文中建立的有限元模型可以较好地模拟钢板-混凝土组合板的承载能力和变形性能.

（2）钢板剥离破坏仅发生在抗剪连接件不完全剪力连接时的板件，在完全剪力连接情况下，钢板与混凝土截面抗剪承载力充足，两种材料协同工作能力良好，能充分发挥两种材料的性能.在这种情况下，钢板剥离不会成为试件破坏的诱因.

（3）在跨中单点（两点对称）加载情况下，当λ＜7.5（λ＜7）时，截面抗剪承载力不足，抗弯承载力较抗剪承载力充足，试件发生剪切破坏；当7.5＜λ＜10（7＜λ＜9）时，截面抗剪承载力不足，抗弯承载力较抗剪承载力不足，试件发生弯剪破坏；当λ＞10（λ＞9）时，截面抗剪承载力充足，抗弯承载力不足，试件发生弯曲破坏.

（4）文中提出的单点或两点加载情况下简支组合板发生各种破坏形态的剪跨比阈值与前期试验结果吻合良好，可为工程设计提供参考.

［1］ Casillas J，Siess C P，Khachaturian N.Studies of reinforced concrete beams and slabs reinforced with steel plates［J］. Civil Engineering Studies，1957，134（7）：56-62.

［2］ 杨勇，聂建国，杜明珠，等.闭口型压型钢板-混凝土组合板疲劳性能试验研究［J］.土木工程学报，2010，41（12）：35-41. Yang Yong，Nie Jian-guo，Du Ming-zhu，et al.Experimental study on fatigue performance of closed profiled steel sheeting-concrete composite slabs［J］.China Civil Engineering Journal，2010，41（12）：35-41.

［3］ 杨勇，聂建国，杨文平，等.闭口型压型钢板-轻骨料混凝土组合板受力性能及动力特性试验研究［J］.建筑结构学报，2008，29（6）：49-55. Yang Yong，Nie Jian-guo，Yang Wen-ping，et al.Experimental study on mechanical behavior and vibration characteristic of re-entrant trough profiled steel sheeting-light weight concrete composite slabs［J］.Journal of Building Structures，2008，29（6）：49-55.

［4］ 易卫华，聂建国，彭惠玲.闭口型压型钢板-混凝土组合板的受弯性能［J］.工业建筑，2003，33（12）：11，22-23. YiWei-hua，Nie Jian-guo，Peng Hui-ling.Bending behavior of closed profiled sheeting-concrete composite slabs［J］. Industrial Construction，2003，33（12）：11，22-23.

［5］ 吴丽丽，聂建国.四边简支钢-混凝土组合板的弹性局部剪切屈曲分析［J］.工程力学，2010，27（1）：52-57. Wu Li-li，Nie Jian-guo.Elastic local shear buckling analysis on simply supported steel-concrete composite slab［J］.Engineering Mechanics，2010，27（1）：52-57.

［6］ 吴丽丽，聂建国.钢-混凝土组合板的弹性剪切屈曲分析［J］.华南理工大学学报：自然科学版，2011，41（3）：622-629. Wu Li-li，Nie Jian-guo.Analysis of key parameters of nontension prestressing technology for continuous steel-concrete composite beams［J］.Journal of South China University of Technology：Natural Science Edition，2011，41（3）：622-629.

［7］ 左莹.压型钢板-混凝土组合板的研究［D］.北京：清华大学土木水利学院，2007.

［8］ 杨悦，刘晶波，樊健生，等.钢板-混凝土组合板受弯性能试验研究［J］.建筑结构学报，2013，34（10）：24-31. Yang Yue，Liu Jing-bo，Fan Jian-sheng，et al.Experimental study on flexural capacity of steel plate-concrete composite slabs［J］.Journal of Building Structures，2013，34（10）：24-31.

［9］ 马晓伟，聂建国，陶慕轩，等.双钢板-混凝土组合剪力墙压弯承载力数值模型及简化计算公式［J］.建筑结构学报，2013，34（4）：99-106. Ma Xiao-wei，Nie Jian-guo，Tao Mu-xuan，et al.Numerical model and simplified formula of axial force-moment capacity of composite shearwallwith double steel plates and infill concrete［J］.Journal of Building Structures，2013，34（4）：99-106.

［10］ 胡红松，聂建国.双钢板-混凝土组合剪力墙变形能力分析［J］.建筑结构学报，2013，34（5）：52-62. Hu Hong-song，Nie Jian-guo.Deformability analysis of composite shear walls with double steel plates and infill concrete［J］.Journal of Building Structures，2013，34（5）：52-62.

［11］ Uy B.Behavior and design of high strength steel-concrete composite columns［C］∥Proceedings of11th International Conference on Steel and Composite Structures.Seoul：Taylor&Francis Group，2012：111-124.

［12］ Liang Q Q，Uy B，Wright H D，et al.Local and post-local buckling of double skin composite panels［J］.Proceedings of the Institution of Civil Engineers-Structures and Buildings，2003，156（2）：111-119.

［13］ Liang Q Q，Uy B，W right H D，et al.Local buckling of steel plates in double skin composite panels under biaxial compression and shear［J］.Journal of Structural Engineering，2004，130（3）：443-451.

［14］ 戴万江，何雄君，毛昌庆.FRP筋混凝土粘结滑移有限元分析［J］.交通科技，2010（2）：78-81. DaiWan-jiang，He Xiong-jun，Mao Chang-qing.Finite element analysis on bond-slip properties of FRP concrete［J］. Transportation Science&Technology，2010（2）：78-81.

［15］ Ollgaard JG，Slutter R G，Fisher JW.Shear strength of stud connections in light weight and normal weight concrete［J］.Journal of American Institute of Steel Construction，1971，8（4）：55-64.

Failure M odes Analysis of Steel Plate-Concrete Composite Slabs Under Transverse Concentrated Load

Wu Li-li Liu Yan Jiang Yu-peng Zhang Dong-dong
（State Key Laboratory for Geomechanics and Deep Underground Engineering∥School of Mechanics and Civil Engineering，China University of Mining and Technology（Beijing），Beijing 100083，China）

By combining the ANSYS-based finite elementmethod with the test，the changes of the flexural bearing capacity and shear bearing capacity of specimens with the shear-span ratio are analyzed，and the influence of the shear-span ratio on the failuremode of specimens is investigated respectively under single-point and two-point symmetric loading on themidspan.The results show that（1）the debonding failure of steel plates occurs onlywhen the shear connection are not complete；（2）under the single-point（two-point symmetric）loading on themidspan with a shear-span ratio of less than 7.5（7），the flexural bearing capacity of section ismore sufficient than the shear bearing capacity，so the shear failure of specimens occurs；（3）when the shear span ratio is between 7.5（7）and 10（9），neither the flexural bearing capacity of section nor the shear bearing capacity is sufficient，so the bending shear failure of specimens occurs；and（4）when the shear span ratio ismore than 10（9），the flexural bearing capacity of section ismore insufficient than the shear bearing capacity，so the bending failure of specimens occurs.

steel plate-concrete composite slab；shear-span ratio；flexural bearing capacity；shear bearing capacity；flexural behavior；failuremodes

TU 398.9；TU 317.1

10.3969/j.issn.1000-565X.2015.07.010

1000-565X（2015）07-0068-07

2014-10-28

国家自然科学基金资助项目（51278488）；北京高等学校青年英才计划项目（YETP0942）

Foundation item：Supported by the National Natural Science Foundation of China（51278488）

吴丽丽（1977-），女，博士，副教授，主要从事钢结构、钢-混凝土组合结构等方面的研究.E-mail：jennywll@163.com