常规桥梁平面梁格法模型横向刚度的精确调整方法

黎力韬，朱思蓉

(广西交通科学研究院，广西　南宁　530007)



常规桥梁平面梁格法模型横向刚度的精确调整方法

黎力韬，朱思蓉

(广西交通科学研究院，广西南宁530007)

黎力韬(1988—)，硕士研究生，主要从事桥梁试验检测工作；

朱思蓉(1987—)，助理工程师，主要从事桥梁试验检测工作。

摘要：荷载试验最主要试验对象为常规桥梁(T梁、小箱梁、空心板)。为了得到控制梁片在设计荷载下的计算挠度和应变，通常采用平面梁格法模型进行计算，然而，模型中横向联系刚度模拟的不准确，会使现场对试验结果的判断产生偏差，使桥梁缺陷无法及时被诊断。文章以大量荷载试验得出的试验数据为根据，提出用平面梁格法模型建立常规桥梁时更精确的横向联系建模调整方法。

关键词：常规桥梁；平面梁格法；横向联系单元；调整

0引言

当前，荷载试验作为检验桥梁整体受力性能和桥梁承载力是否达到要求的直接方法，已经被广泛接受和使用。荷载试验既可针对新建桥梁，亦可针对旧桥、病害桥梁进行荷载试验，检验其施工质量是否满足设计要求，检验其是否满足现行规范荷载等级标准。荷载试验的检测结果可以为桥梁运营的安全性提供技术依据，并为今后桥梁维护、管理提供原始资料。

荷载试验的判断结果主要基于试验现场第一时间测得的桥梁反应。在分级加载的试验程序下，测出桥梁在各级荷载下的静态、动态反应，发现可能存在的桥梁病害和缺陷；若试验数据显示桥梁有重大缺陷，试验方案需要进行适当调整，必要时可以终止试验，以保证试验安全。考虑到试验现场第一时间分析和判定的重要性，建立准确的判定依据尤为重要。判定依据来源于有限元计算模型。常规桥梁(如T梁桥、小箱梁桥和空心板梁桥)作为最常使用的桥型，自然也是荷载试验最主要试验对象。这类桥梁通常都使用平面梁格法建模计算。平面梁格法建模简单高效，能为荷载试验提供设计荷载等级下的理论计算挠度和应变值，目前已经是大多数常规桥梁的建模选择。因为荷载试验结果的判定直接依赖于计算模型的精准度，所以只有合理的模型才能得出可靠的试验结论。

1现行常规桥梁平面梁格法建立模型的不足

平面梁格法能较好地模拟常规桥梁的传力分布特征，其简单、高效的特点注定了这种建模方法在数目庞大的常规桥梁荷载试验项目中成为计算方法首选。平面梁格法模型中，纵桥向单元的建模思路已比较成熟，即考虑完整的纵梁及70%左右的桥面铺装的贡献，其余桥面只考虑其在质量上对结构的影响。该思路已较为成熟并被广泛应用。

与纵桥向单元不同的是，横向虚拟联系单元在建模过程中则缺乏统一精确的建模思路。通常，小箱梁与T梁之间的横向联系单元只考虑湿接缝截面刚接联系，空心板梁之间的横向联系单元只考虑顶板或顶板+底板截面的铰接联系，三种截面形式在桥面对横向单元截面的贡献上采用与纵向单元一样的方式考虑。然而，小箱梁、T梁、空心板这三类桥梁在横向受力上都有不同的受力特点，此外结构与路线的交角对横向单元的设定也有影响。将近年来荷载试验的实测值与计算模型所提取的计算值进行对比，发现部分按照常规思路建模得出的模型横向联系刚度偏小。这个差别会直接影响试验结果第一时间的判断，错过在加载条件下对桥梁缺陷诊断的最好时机。虽然模型可以在试验后调整修正，但工程人员却失去了现场发现问题的最好时机。模型调整后的二次检测可以使结果更可靠，却会带来大量的复工成本。

蒙屯大桥与头孔1#中桥试验跨在试验荷载作用下挠度与应变的实测值和计算值的横向分布对比图见图1。

从图1中可以看出，这两座桥梁的计算挠度的横向分布反应出计算模型考虑的横向刚度小于实际结构。对于蒙屯大桥偏心加载工况，控制梁片为6#T梁；对于头孔1#中桥对称加载工况，控制梁片为5#、6#空心板。计算模型横向刚度的不足会使控制梁片的校验系数偏小(校验系数=实测值/计算值)，远离控制梁片的梁校验系数偏大(蒙屯大桥的1#梁校验系数甚至>1.0)。荷载试验现场数据处理量较大，通常都只以控制梁片的校验系数作为依据作最直接的判断，此时因为模型横向刚度不足导致的校验系数偏小，将可能导致判断不准。若桥梁状况较差，这种误判可能检测人员错过最佳的诊断时机，试验的继续进行甚至会带来结构的破坏，带来不可挽回的损失。

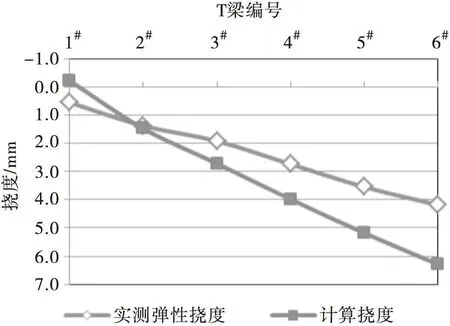
蒙屯大桥(偏心加载)

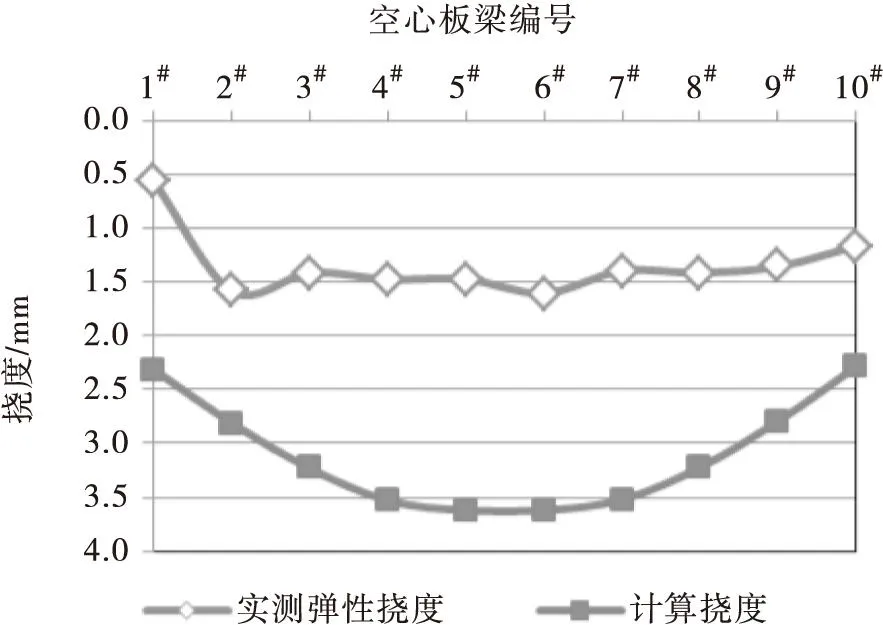
头孔1#中桥(对称加载)

2基于荷载试验数据修正常规桥梁平面梁格法模型

由T梁、小箱梁、空心板这三类构件构成上部结构的桥梁占桥梁总数的绝大部分，它们自然也成为了荷载试验的重点对象。建立拥有准确的模型将有助于更好地检测和判定这些桥梁的状况和承载能力。

本文从大量荷载试验数据中挑选出具有代表性的实例进行分析，这些试验中的桥梁状况良好，挠度和应变的横向分布较为平滑且有规律，说明桥梁整体性较好。同时，这些桥梁的计算模型均能很好地模拟出桥梁的传力情况。水泡水库大桥与茅岭互通跨线桥试验跨在偏心加载和对称加载下的实测值与计算值对比图见图2。

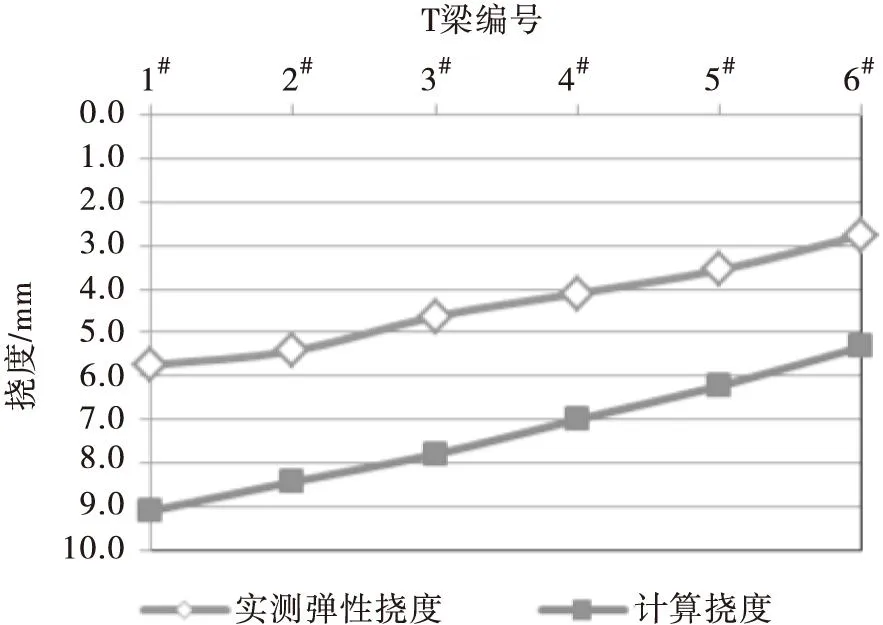
水泡水库大桥(偏心加载)

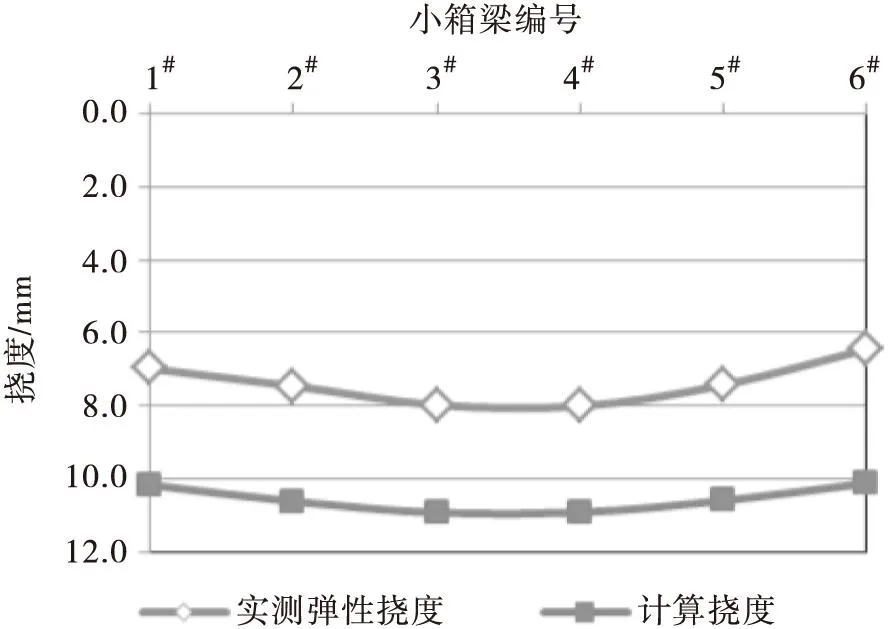
茅岭互通跨线桥(对称加载)

从图2中可以发现这两组试验实测值与计算值横向分布趋势相同。若将第i片梁的实测值称作Ti，计算值称作Ci，实测值最大值为Tmax，计算值最大值为Cmax，为统一标准，作归一化处理，将与均除以和的较大者设为F。则可用归一化后对应梁片的计算值与实测值的差值的绝对值的方差来判定实测值与计算值差值的离散程度，即可作为评判横向联系刚度是否模拟准确的依据。为了方便比较，将计算出来的方差乘上100作为模型横向刚度评价系数D。

则D的表达式为：

(1)

(其中n为梁片的数量)

从图形上分析，若实测值横向分布较为平缓，且实测值与计算值趋势相同，则D值会比较小；反之若实测值与计算值趋势相差大，模型横向刚度与真实结构相差较大，则D会较大。本文第一节列出的蒙屯大桥和头孔1#中桥的D值分别为1.07和1.58，第二节列出的水泡水库大桥与茅岭互通跨线桥的D值分别为0.09和0.05。

通过大量荷载试验测数据的比对分析，结合各座桥梁所对应的计算模型，本文接下来将提出分别针对T梁、小箱梁、空心板梁这类型的桥梁在建模时如何调整使模型能够具有与真实结构相近的横向刚度，即模型横向刚度评价系数D能维持在一个较小值。

2.1　平面梁格法中T梁模型横向联系刚度调整

一般情况下，平面梁格法在建立T梁模型时横向联系单元的截面通常考虑为单位长度的湿接缝纵剖截面加上70%左右的混凝土桥面铺装层的贡献。但是，根据大量荷载试验所测出的T梁试验跨的挠度、应变实测弹性值的横向分布表明，该方法建立的模型的横向刚度小于真实桥梁，因为平面梁格法基于的平面杆系模型，无法很好模拟出实体结构的横向传力机制。

基于14座施工质量良好、承载能力满足要求的T梁桥荷载试验的数据与对应模型调整结果，本文提出以下针对T梁桥建模的建议：

(1)对于直桥，横向联系单元可以使用矩形截面梁单元建立，横向联系单元与纵梁垂直，单元截面宽度为横向单元间距长度(建议≤1.0 m)，截面高度为全部桥面铺装与T梁翼缘板最大厚度之和的2.0~2.5倍，全部桥面铺装需包括沥青铺装层的厚度。

(2)对于斜桥，横向联系单元应与纵梁相互垂直，这意味着测试截面方向(与同排支座布置方向相同)与横向联系单元件存在夹角。此时桥梁横向刚度将由纵梁刚度和横向联系单元刚度综合构成。从荷载试验数据对比可知，T梁斜桥的横向联系单元截面可选用矩形截面，截面宽度为横向单元间距长度(建议≤1.0 m)，截面高度为T梁翼缘板最大厚度与80%混凝土桥面铺装之和。

(3)横隔板单元的截面高度参照横向联系单元设置，对桥面铺装进行放大考虑。

经过修正，技术状况良好的T梁桥与对应模型的横向刚度评价系数D降低约80%，维持在0.20之内。

2.2　平面梁格法中小箱梁模型横向联系刚度调整

与T梁模型类似，由数片小箱梁组成的桥梁上部结构模型的横向联系单元的设置也有讲究。若按照湿接缝单位长度截面作为单元截面尺寸建模，同样会遇到模型横向刚度偏小的问题。基于10座施工质量良好、承载能力满足要求的小箱梁桥荷载试验的数据与对应模型调整结果，本文提出以下针对小箱梁桥建模的建议：

(1)对于直桥，横向联系单元可以采用矩形截面梁单元形式。横向联系单元与纵梁垂直，单元截面宽度为横向单元间距长度(建议≤1.0 m)，截面高度为全部桥面铺装与T梁翼缘板最大厚度之和的1.5倍，全部桥面铺装需包括沥青铺装层的厚度。

(2)对于斜桥，与T梁类似，桥梁真实的横向刚度在模型里是由纵向和横向单元综合贡献。通过对试验数据和模型的分析，这类桥梁的横向联系单元的建立应与纵梁垂直，采用矩形截面，截面宽为横向单元间距长度(建议≤1.0 m)，高度为湿接缝厚度。此外，混凝土桥面铺装采用板单元，考虑80%左右的混凝土铺装层厚度对横向刚度的贡献。剩余的20%混凝土铺装层和沥青层对横向刚度贡献不予以考虑。

(3)横隔板单元的截面高度参照横向联系单元设置。

经过修正，技术状况良好的小箱梁桥与对应模型的横向刚度评价系数D降低约60%，维持在0.20之内。

2.3　平面梁格法中空心板模型横向联系刚度调整

与T梁及小箱梁通过湿接缝进行横向联系的方式不同，空心板之间设置有铰缝，相邻空心板间横向上通过铰缝与桥面系相互作用。因为铰缝的受力特点，使用平面梁格法建立空心板梁桥模型时横向单元间通常采用铰接联系。横向联系单元通常采用矩形或工字型截面以模拟顶板或顶板底板的共同作用。但是，此方法建立模型横向刚度较弱，正载工况下计算值横向趋势图中间测点下凹，偏载工况下控制端计算值远大于非控制端。实测值的横向分布表明实际结构拥有较大的横向刚度，横向分布曲线平缓，测量结果与通过横向分布系数计算得出结果相呼应。

基于9座施工质量良好、承载能力满足要求的空心板梁桥荷载试验的数据与模型调整结果，本文提出以下针对空心板梁桥建模的建议：

(1)对于直桥与斜桥，横向联系单元与纵梁垂直，单元截面宽度为横向单元间距长度(建议≤1.0 m)，截面高度为全部混凝土桥面铺装与空心板顶板最大厚度之和，横向刚度不计入沥青铺装层的贡献。

(2)将各空心板抗扭刚度Ixx做等比例调整，使所有空心板抗扭刚度之和与整体截面抗扭刚度之和相当。

经过修正，模型横向刚度评价系数D降低约30%。正载工况下D<0.7，偏载工况下D<3.0。相较于T梁与小箱梁模型调整的结果，空心板梁桥模型D值偏大。因为实际结构相邻空心板通过铰缝作用，而铰缝由素混凝土构成，无法达到理想的传力状况，使实测值横向趋势波动，则D值结果不可能控制在较小范围内。

3结语

本文通过分析数十座技术状况与承载能力满足要求的常规桥梁的荷载试验实测值，以及平面梁格法所建立模型得出的计算值，提出了针对各类T梁桥、小箱梁桥与空心板梁桥的平面梁格法建模技巧，使模型能够更好地模拟试验桥梁在良好技术状况时，在试验荷载下的挠度与应变值。基于更可靠的模型计算值，能使荷载试验第一现场的判断更准确、及时，确保检测工作抓住最好的试验时机，发现桥梁隐蔽的缺陷，为试验检测工作提供更好的支持。

参考文献

[1]李国豪.公路桥梁荷载横向分布计算[M].北京：人民交通出版社，1984.

[2]张剑超.关于桥梁荷载横向分布系数的研究[D].武汉：武汉理工大学，2011.

[3]李淑芬.带翼小箱梁桥荷载横向分布计算分析及其试验研究[D].成都：西南交通大学，2007.

[4]蒋国富.钦州至崇左高速公路屯蒙大桥桥梁试验检测报告[R].南宁：广西交通科学研究院，2013.

[5]蒋国富.百色至靖西高速公路K31+540头孔1号中桥试验检测报告[R].南宁：广西交通科学研究院，2015.

[6]李保军.宜州至河池高速公路河池西互通C匝道桥(8#跨)试验检测报告[R].南宁：广西交通科学研究院，2014.

[7]蒋国富.防城至东兴高速公路茅岭互通跨线桥试验检测报告[R].南宁：广西交通科学研究院，2013.

[8]蒋国富.河池至都安高速公路K19+926处水泡水库大桥试验检测报告[R].南宁：广西交通科学研究院，2014.

[9]蒋国富.玉林至铁山港高速公路K115+830山心大桥桥梁试验检测报告[R].南宁：广西交通科学研究院，2013.

[10]李保军.县道894线九圩至隘洞K60+395板伦中桥桥梁试验检测报告[R].南宁：广西交通科学研究院，2014.

Accurate Adjustment Method of Transverse Stiffness for Conventional Bridge Plane Grillage Method Model

LI Li-tao，ZHU Si-rong

(Guangxi Transportation Research Institute，Nanning，Guangxi，530007)

Abstract：The main experimental object of load test is the conventional bridge(T beams，small box girder，hollow plate).In order to obtain the calculated deflection and strain of control beams under the design load，generally the plane grillage method model is used for calculations，however，the inaccurate horizontal linkage stiffness simulation in this model will cause the on-site determination bias on test results，so that the bridge defect can not be diagnosed in a timely manner.Based on the large number of experimental data obtained from load test，this article proposed the more precise horizontal linkage modeling adjustment method when establishing the conventional bridge by using the plane grillage method.

Keywords：Conventional bridge； Plane grillage method； Horizontal linkages element； Adjust

收稿日期：2015-04-04

文章编号：1673-4874(2015)05-0057-04

中图分类号：U445

文献标识码：A

DOI：10.13282/j.cnki.wccst.2015.05.016

作者简介