低压排汽缸气动优化设计
2015-03-14杨建道陈涛文宋立明李军
杨建道,陈涛文,宋立明,李军
(西安交通大学叶轮机械研究所,710049,西安)
低压排汽缸气动优化设计
杨建道,陈涛文,宋立明,李军
(西安交通大学叶轮机械研究所,710049,西安)
结合三阶贝齐尔曲线参数化方法、静压恢复系数评价方法、拉丁立方试验设计、三阶响应面近似模型及Hooke-Jeeves直接搜索算法的组合优化策略,基于iSight优化软件平台,建立了排汽缸外导流环优化设计系统。以静压恢复系数最大为目标完成了单独排汽缸优化设计,采用数值求解三维Reynolds-Averaged Navier-Stokes(RANS)方程的方法验证了耦合低压末级和排汽缸结构的排汽缸优化设计系统的有效性。结果表明,基于优化设计系统进行的优化设计,使得排汽缸静压恢复系数相对于初始排汽缸提高了61.1%,排汽缸蜗壳内的静压损失明显减小,从而验证了排汽缸优化设计的有效性和耦合低压末级对排汽缸气动性能分析的必要性。
排汽缸;静压恢复;优化设计;数值模拟
冷凝式汽轮机排汽缸的主要功能是将低压末级出口的蒸汽动能转化为压力能,在凝汽器真空度给定的条件下,可降低末级出口截面处的静压,增加末级的出力,提高汽轮机机组的热效率。大功率汽轮机低压缸末级出口平均绝对马赫数为0.5~0.8,其排汽动能约占机组总焓降的1.5%,如果能有效地回收、利用这部分能量,可以使机组的热效率提高约1%。因此,高性能排汽缸设计是提高汽轮机能量转换效率的重要技术手段[1]。
图1给出了典型的大功率汽轮机低压缸三维结构图。静压恢复主要在排汽缸的扩压器导流环中完成,还有一部分在排汽缸的蜗壳中完成。蒸汽在该结构的排汽缸内流动是先轴向再径向流向凝汽器。科研人员采用实验测量[2]和数值模拟[3]等方法研究了排汽缸内的三维流动形态和损失产生机理。

图1 汽轮机低压缸三维结构图
随着优化设计方法和计算机技术的进步,提高排汽缸静压恢复系数的优化设计得到了发展。陈川等采用正交试验设计、二次多项式响应面近似评价方法和二次规划的组合优化策略对排汽缸进行了优化设计,以提高排汽缸的静压恢复能力[4]。Wang等采用改进的Kriging和小生境微种群遗传算法对模型排汽缸导流环进行了优化设计[5]。Yoon等应用Alstom公司的EDS(in-house exhaust design system)对排汽缸扩压器进行了设计,优化设计中考虑了末级叶片和排汽缸耦合的三维气动性能[6]。Mizumi等研发了末级叶片和扩压器耦合设计方法[7]。Verstraete等采用计算流体动力学(CFD)、排汽缸扩压器型线参数化和遗传算法优化设计了排汽缸扩压器导流环的型线,分析了优化后排汽缸在设计工况和变工况下的气动性能[8]。
排汽缸的三维优化设计中往往没有考虑低压末级与排汽缸的相互影响。因此,本文采用了拉丁立方试验设计、三阶响应面近似模型、Hooke-Jeeves直接搜索算法的组合优化策略对排汽缸外导流环进行了非轴对称优化设计。采用耦合低压末级与排汽缸整体结构对优化设计结果进行了详细的数值验证,以证明排汽缸优化设计的有效性和耦合低压末级对排汽缸气动性能分析的必要性。
1 低压排汽缸优化设计系统
图2给出了排汽缸优化设计流程。首先采用拉丁立方试验设计对设计空间进行取样,再由CFD求解样本点得到目标变量值后建立初始的三阶响应面近似模型,之后用Hooke-Jeeves直接搜索算法搜索出最优近似解,并用CFD对搜索出的最优近似解进行校核。当CFD计算得出的结果与优化算法得出的最优近似解的相对误差小于等于1.0%时,即可认为优化收敛。若误差较大,则将CFD计算值放入初始样本库中更新响应面近似模型,重新搜索,如此迭代,直到优化收敛为止。图2排汽缸设计系统是建立在iSight软件平台上的。排汽缸导流环三阶贝齐尔曲线参数化方法是自编程序通过iSight设计变量接口进行调用的,排汽缸静压恢复系数的CFD评价方法是调用ANSYS-CFX软件进行的。拉丁立方试验设计和三阶响应面近似模型是基于iSight软件平台建立的,Hooke-Jeeves直接搜索算法的搜索方法是采用iSight软件提供的优化方法。

图2 排汽缸优化设计系统
1.1 气动性能评价
图3给出了排汽缸的计算模型及单独排汽缸计算时的边界设置。优化的主要几何结构为扩压器外导流环,优化时的进汽条件为单独排汽缸均匀进汽的条件。Reynolds-Averaged Navier-Stokes(RANS)方程采用CFD软件ANSYS-CFX求解,湍流模型采用Scalable壁面函数的标准k-ε模型,对流项采用二阶精度格式,工质为平衡态湿蒸汽。

(a)计算模型 (b)边界设置图3 排汽缸计算模型及单独排汽缸计算时的边界设置
图4给出了单独排汽缸初始静压恢复系数随网格数的变化。由图4可知,当网格数达到231万时,静压恢复系数已基本达到网格无关解。所以,最终确定的计算网格数为231万。静压恢复系数
(1)
式中:Pout为排汽缸出口静压;Pin为进口静压。

图4 单独排汽缸初始静压恢复系数随网格数的变化
1.2 参数化方法
图5给出了排汽缸外导流环控制点及其变化区域。外导流环曲线为三阶贝齐尔曲线,由4个控制点P1、P2、P3、P4控制。考虑到扩压器进口保持不变,P1固定不动,P4坐标用扩压器出口宽度D及出口高度H控制。为了更好地控制H及D的变化,令h4=H/L,d4=D/L,L为扩压器进口高度,P4最终由参数h4及d4控制。P2、P3的变化范围由多边形P1PC2PC3P4控制,即由区域A决定;P2、P3可在区域A内任意变化,但P3的y坐标必须大于等于P2的y坐标;PC2的y坐标与P1相同,PC2的x坐标为P1的x坐标加上2 900 mm,这一范围已足够大;PC3的x坐标与PC2相同,PC3的y坐标与P4相同。

图5 外导流环控制点及其变化区域
对外导流环的非轴对称优化分为2个步骤:①轴对称优化设计,由此得到轴对称最优外导流环;②非轴对称优化设计。图6给出了非轴对称外导流环造型方法,其中包括曲面1~3,曲线1~3。曲面2为轴对称优化时得到的最优型面,非轴对称优化时曲面2保持不变;曲线1~3为曲面3的控制曲线,曲线3的控制参数固定,与曲面2的控制曲线相同;曲线1、2为三阶贝齐尔曲线,控制方法如图5所示,曲线1、2的控制变量相同,变化规律相同。曲面1由曲线1绕转子转轴旋转一定角度后得到,且随着曲线1的变化而变化(曲面1并不是外导流环壁面的一部分,它的作用主要是对曲面3进行约束)。曲面3与曲面1、2的相交处为一阶导数连续。曲面2、3组成外导流环曲面。以上造型在三维造型软件UG中完成。

图6 非轴对称外导流环造型方法
2 优化结果与验证
静压恢复系数是衡量排汽缸气动性能的重要指标,可作为排汽缸的优化设计中的优化目标变量。
首先对外导流环进行轴对称优化设计,优化时选用了40个样本点构建初始化的响应面模型(RSM),然后对响应面模型最优解进行14次CFD校核,CFD计算值与响应面模型最优解的最终相对误差为0.266%。图7a为轴对称优化时响应面模型与CFD校核值的收敛曲线。在得到轴对称最优外导流环后按图6方法进行非轴对称优化设计,优化时选用了40个样本点构建初始化的响应面模型,然后对响应面模型最优解进行8次CFD校核,CFD计算值与响应面模型最优解的最终相对误差为0.75%。图7b为非轴对称优化时响应面模型与CFD校核值的收敛曲线。

(a)轴对称优化

(b)非轴对称优化图7 响应面模型最优解与CFD校核值收敛曲线
图8给出了优化前、后中分面处外导流环上、下型线的几何参数对比。图9给出了优化前、后外导流环的三维结构对比。由图9可知:优化后,外导流环的起始扩散角明显减小,在大部分周向范围内出口宽度减小,在下半部小部分区域内出口宽度略有增大;优化后的扩压器流道有所增大。

(a)上型线

(b)下型线图8 优化前、后中分面外导流环上、下型线的几何参数对比
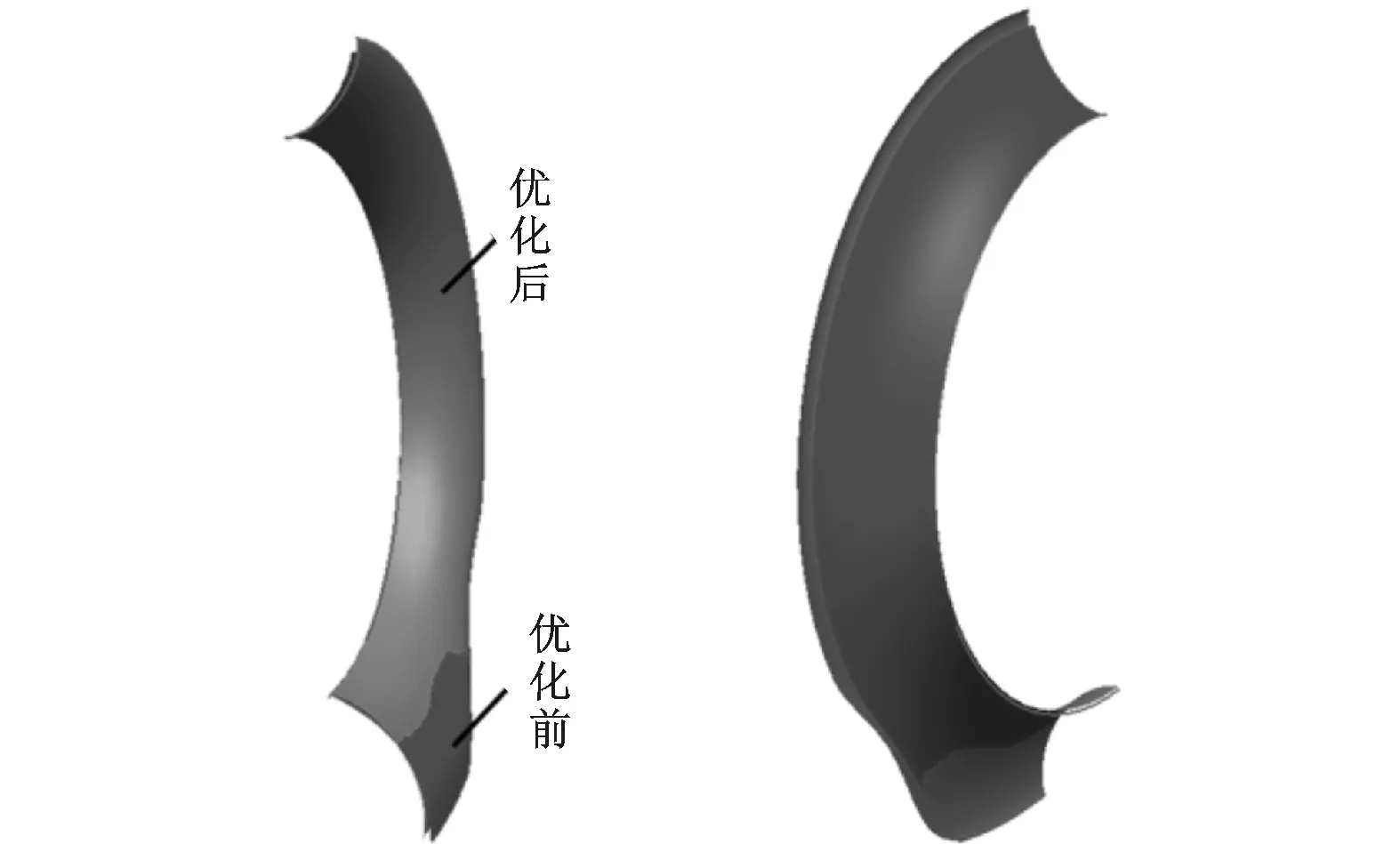
图9 优化前、后外导流环三维结构对比
图10给出了耦合末级整圈与动叶叶顶汽封的边界条件设置及各计算域网格示意。表1给出了各计算域网格数。表2给出了单独排汽缸及耦合末级整圈与动叶叶顶汽封2种模型的进、出口边界条件设置。
表3给出了优化前、后2种计算模型下排汽缸的静压恢复系数。由表3可知: 优化后排汽缸的静压恢复系数得到了显著提高;单独排汽缸优化后,静压恢复系数相对提高了72.78%;耦合末级整圈与动叶叶顶汽封后,静压恢复系数相对提高了61.1%。

图10 耦合末级整圈与动叶叶顶汽封的边界条件设置及各计算域网格示意

计算域静叶动叶动叶叶顶汽封排汽缸节点总数节点数269万596万245万428万1540万

表2 2种模型进、出口边界条件设置

表3 2种模型下优化前、后排汽缸的静压恢复系数

图11 优化后单独排汽缸及耦合末级整圈与动叶叶顶汽封的截面位置示意

(a)单独排汽缸 (b)耦合末级整圈与动叶叶顶汽封 图12 优化后单独排汽缸及耦合末级整圈与动叶叶顶汽封的截面1流线图
对于耦合末级整圈及动叶叶顶汽封,排汽缸静压恢复系数有所下降,主要原因是单独排汽缸的进汽条件是周向均匀的,耦合末级整圈与动叶叶顶汽封后进汽条件有所改变,从而导致缸内流场发生变化。图11给出了优化后单独排汽缸及耦合末级整圈与动叶叶顶汽封的截面位置示意。图12给出了优化后单独排汽缸及耦合末级整圈与动叶叶顶汽封的截面1的二维流线图。对于耦合末级整圈与动叶叶顶汽封,旋涡1明显增大,从而导致耦合末级整圈与叶顶汽封的排汽缸静压恢复系数略有下降。因此,在进行排汽缸的优化设计时应当尽量采用接近真实的进汽条件。

(a)优化前 (b)优化后 图13 耦合末级整圈与叶顶汽封优化前、后截面1静压系数分布
图13、14给出了耦合末级与动叶叶顶汽封优化前、后截面1和截面2的静压系数分布。该静压系数
(2)
静压系数越大,表明静压越大,静压恢复越好。由图13、14可知,尽管优化前、后扩压器流道内的静压系数差别不大,但优化后排汽缸涡壳内的静压系数提高,表明优化后蜗壳内的流动得到了明显的改善,静压损失明显减小。

(a)优化前
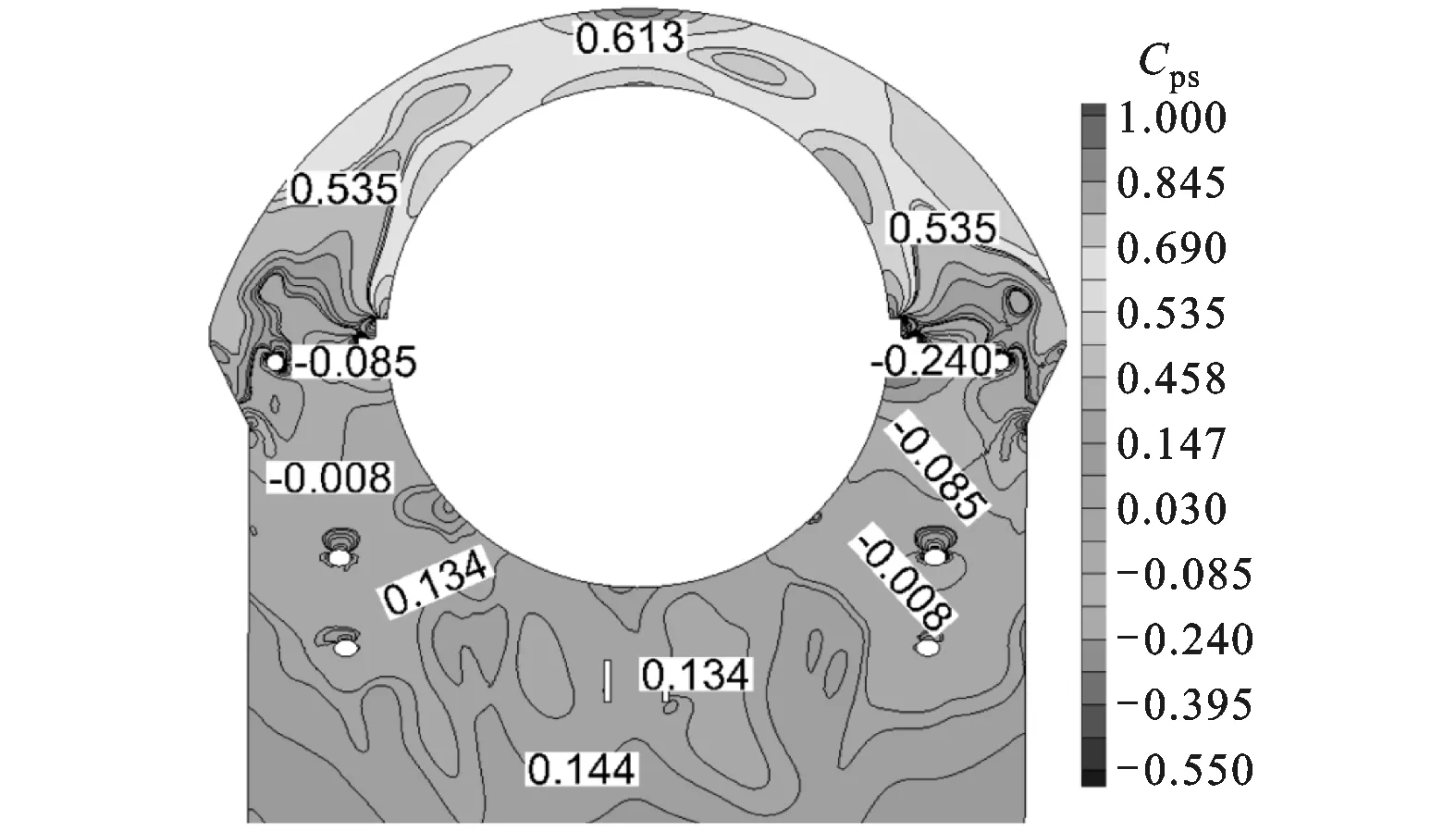
(b)优化后 图14 耦合末级整圈与动叶叶顶汽封优化前、后截面2静压系数分布
3 结 论
本文采用拉丁立方试验设计、三阶响应面近似模型和Hooke-Jeeves直接搜索算法的组合优化策略,对排汽缸扩压器外导流环进行了非轴对称优化设计,得到如下结论。
(1)非轴对称优化后,静压恢复系数得到了显著提高,单独排汽缸优化后,静压恢复系数由0.158提高到0.273,相对提高了72.78%;耦合末级整圈与动叶叶顶汽封后,静压恢复系数由0.149提高到0.24,相对提高61.1%,表明优化系统是有效的。
(2)耦合末级整圈与动叶叶顶汽封的静压恢复系数略有下降,表明优化时应当尽可能采用接近真实的进汽条件。
(3)优化前、后扩压器流道内流动相似,但优化后蜗壳内的流动损失明显减小,从而使得排汽缸总体性能得到明显提高。
[1] BURTON Z, INGRAM G L, HOGG S. A literature review of low pressure steam turbine exhaust hood and diffuser studies [J]. ASME Journal of Engineering for Gas Turbines and Power, 2013, 135(6): 062001.
[2] FINZEL C, SCHATZ M, CASEY M V, et al. Experimental investigation of geometrical parameters on the pressure recovery of low pressure steam turbine exhaust hood, GT2011-45302 [R]. New York, USA: ASME, 2011.
[3] LI J, LI Z, FENG Z. Effects of the last stage rotor tip leakage flow on the aerodynamic performance of the exhaust hood for steam turbines, GT2013-94377 [R]. New York, USA: ASME, 2013.
[4] 陈川, 付经伦, 刘建军. 汽轮机排汽系统优化设计与性能分析 [J]. 工程热物理学报, 2009, 30(8): 1295-1298. CHEN Chuan, FU Jinglun, LIU Jianjun. Optimal design and performance analysis of steam turbine exhaust system [J]. Journal of Engineering Thermophysics, 2009, 30(8): 1295-1298.
[5] WANG H, ZHU X, DU Z, et al., Aerodynamic optimization system development for low pressure exhaust hood of steam turbine, GT2010-22280 [R]. New York, USA: ASME, 2010.
[6] YOON S, STANLSLAUS F J, MOKULYS T, et al. A three-dimensional diffuser design for the retrofit of a low pressure turbine using in-house exhaust design system, GT2011-45466 [R]. New York, USA: ASME, 2011.
[7] MIZUMI S, ISHIBASHI K. Design philosophy and methodology of a low pressure exhaust hood for a large power steam turbine, GT2013-94303 [R]. New York, USA: ASME, 2013.
[8] VERSTRAETE T, PRINSIER J, DI-SANTE A, et al. Design optimization of a low pressure steam turbine radial diffuser using an evolutionary algorithm and 3D CFD, GT2012-69515 [R]. New York, USA: ASME, 2012.
(编辑 苗凌)
Aerodynamic Optimization on the Low Pressure Exhaust Hood
YANG Jiandao,CHEN Taowen,SONG Liming,LI Jun
(Institute of Turbomachinery, Xi’an Jiaotong University, Xi’an 710049, China)
Combined with three-order Bezier curve parameterization method of exhaust diffuser profile, static pressure recovery coefficient evaluation method, the combinatorial optimization strategy including Latin square design of experiment, three-order response surface approximated model and Hooke-Jeeves optimization method, aerodynamic optimization design of exhaust hood diffuser for steam turbine is established based on the software iSight. Aerodynamic optimization design of exhaust hood is conducted for the maximum of the static pressure recovery coefficient of exhaust hood. The design variables are specified by the exhaust diffuser profile parameterization method. The aerodynamic performance of the optimized exhaust hood and referenced design is numerically calibrated with consideration of the full last stage and rotor tip clearance. The validation of the presented optimization design system of the exhaust hood is demonstrated. The optimization design results show that the static pressure recovery coefficient of the optimized exhaust hood is higher by 61.1% than that of the referenced design with consideration of the upstream last stage influence. The static pressure loss coefficient of the optimized exhaust hood decreases significantly by comparison with the referenced design. The availability of the developed aerodynamic optimization design of the exhaust hood diffuser and necessity of the coupled with the last stage on the aerodynamic performance of the exhaust hood were also validated.
exhaust hood; static pressure recovery; optimization design; numerical simulation
2014-06-25。 作者简介:杨建道(1976—),男,博士生;李军(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(51376144);中央高校基本科研业务费专项资金资助项目。
时间: 2015-01-05
网络出版地址: http:∥www.cnki.net/kcms/detail/61.1069.T.20150105.0844.002.html
10.7652/xjtuxb201503004
TK474.7
A
0253-987X(2015)03-0019-06
