系泊型浮体运动的无网格法数值模型
2015-03-14曹文瑾孙中国席光
曹文瑾,孙中国,席光
(西安交通大学能源与动力工程学院,710049,西安)
系泊型浮体运动的无网格法数值模型
曹文瑾,孙中国,席光
(西安交通大学能源与动力工程学院,710049,西安)
针对系泊型浮体在运动中可能出现的绳索保持绷紧、由绷紧变松弛、保持松弛和由松弛变绷紧等4种状态,基于移动粒子半隐式法基本流固耦合模型,提出了一种刚体运动状态判定机制。对浮体受到绳索牵引而运动受限的情况提出了一种处理方法:按体积分的形式计算流体对浮体的压力、重力和它们的力矩,求解刚体动量方程和转动量方程得到浮体的速度和角速度,浮体因受到绳索作用而径向速度降为零,浮体以切向速度绕绳索固定端旋转。对用单绳系泊的二维浮体在孤立波中的运动进行了数值模拟,捕捉到了上述4种运动状态,可以观测到绳索保持绷紧时绳索与浮体的固连点的轨迹为一段圆弧。同时,浮体在水平、竖直和转动方向3个自由度的运动信息均可以从计算结果中提取研究。数值模拟结果符合物理原理,模型的建立扩展了移动粒子半隐式法的应用范围,为模拟固体运动受限制的流固耦合问题提供了思路。
系泊;浮体;移动粒子半隐式法;流固耦合
浮式防波堤、海上风电平台和船舶等都是常见的浮体。在有风浪的时候,浮体发生运动,实际生产生活和工业实际中通常使用绳索来限制浮体的运动范围,绳索的一端固定,另一端固连在浮体上。由于绳索具有抗拉而不抗压的被动性力学特性,当浮体有越出绳长范围的运动趋势时,绳索中将产生作用力来限制浮体的运动范围不超过绳长,而当浮体在绳长范围内运动时,绳索内不会产生作用力,浮体运动完全自由。
已有学者对完全自由漂浮的浮体做了研究:Lee等用移动粒子半隐式法(Moving Particle Semi-implicit Method, MPS)模拟了方形物块沉入水中的过程,并计算了板状物体落入水中时的冲击载荷[1];Bogner等用玻尔兹曼方法(Lattice Boltzmann Method, LBM)模拟了刚性浮体的漂浮现象[2];Omidvar等用变粒子尺度的光滑粒子水动力学方法(Smoothed Particle Hydrodynamics, SPH)模拟了三维浮体对波浪的运动响应[3]。
也有学者对系泊的浮体进行了研究:Mays等研究了浸没的系泊型三维圆柱形浮体的运动[4];Diamantoulaki等研究了绳索数量和绳索与浮体的连接点数量对浮体运动的影响[5];Peng等用改进的流体体积法(Volume of Fluid, VOF)模拟了由两根绳系泊的浮体在波浪中的运动并与实验数据做了对比[6];Ferreras等研究了浮体在弹性不同的绳索作用下的运动并实验测量了绳索中的应力[7]。
已有的研究都只是针对绳索保持绷紧或绳索保持松弛这两种单一状态下的浮体进行的,然而真实的物理现象还包括绳索在绷紧和松弛两个状态之间发生转变的过程。由于浮体现象中存在运动的物质界面,自由液面也会发生大变形,采用无网格法模拟可以避免网格法中网格重构带来的困难。因此,为了真实地模拟出绳索保持绷紧、由绷紧变松弛、保持松弛和由松弛变绷紧4种状态下的浮体运动,本文在移动粒子半隐式法[8]的基础上构建了一种浮体运动判定机制,对浮体在上述4种状态下的运动进行了系统的建模并通过算例进行了验证。
1 加入流固耦合模型的MPS法
在处理有大变形、自由面、固液界面或物质界面存在运动的流动问题时,网格法由于受到网格调整甚至重构等复杂过程的限制而较难实施。MPS法是一种无网格粒子方法,粒子之间没有固定的拓扑关系,而是在拉格朗日观点下随时间运动并在当地与周围粒子构建新的作用关系。这一特性保证了MPS法可以求解上述复杂流动。MPS法已被应用在自由表面流动、表面张力、气液两相流和流固耦合等多种流动问题中并验证了其正确性[8-13]。
1.1 基本MPS法
MPS法适用于不可压缩流动,控制方程为
(1)

(2)
式中:ρ是密度;μ是动力黏性系数;u是速度;p是压力;f是体积力;t是时间。
以配点法思想将求解区域离散成粒子,每个粒子都携带有物性参数(密度、黏性系数等)、运动学参数(坐标、速度等)和热力学参数(压力等)。粒子之间相互影响的强弱程度由核函数衡量,控制方程中的各项微分算子也基于核函数进行离散求解。本文采用的核函数如下
(3)
式中:r=|rj-ri|是任意两个粒子i和j之间的距离;re是核函数的截断半径。离散形式的梯度算子和拉普拉斯算子如下
(4)
(5)

计算中,首先显式计算动量方程中的黏性项和源项,得到粒子速度和坐标的估算值,然后隐式求解压力泊松方程得到压力,最后根据压力梯度修正粒子的速度和坐标。以时间推进的方式追踪粒子在各时间层的运动,从而得到整场的流动信息。
1.2 流固耦合模型
本文采用一种结合刚体动力学理论的MPS法求解流固耦合问题。关于这种改进的MPS法的具体实现和应用可参考文献[13],本文只作简要介绍。
刚体运动满足的控制方程为
(6)
(7)
式中:m是刚体质量;u和ω是刚体的速度和角速度;F和M是刚体受到的外力和外力矩;下标ls表示流体对刚体的作用,other表示其他外力对刚体的作用。
算法的流程如图1所示:先对固体粒子和流体粒子一起利用基本MPS法求解显式步和隐式步,得到所有粒子的压力。对于流体粒子,计算其压力梯度并代回流体的动量方程修正坐标与速度值;对于固体粒子,按式(8)、(9),利用高斯公式将流体对固体的压力和压力的力矩转化成固体区域内的体积分进行求值
Fls=-∬SpdS=-∭VpdV
(8)
Mls=-∬Srral×pdS=-∭Vrral×pdV
(9)
式中:rral表示固体粒子相对于刚体质心的坐标。将合外力和合外力矩代入刚体运动的动量方程和角动量方程求得刚体的质心速度uc、质心坐标rc和角速度ωc,再由相对坐标可以得到每个固体粒子的速度ui和坐标ri
ui=uc+ωc×rral,i
(10)
ri=rc+Δt(ωc×rral,i)
(11)

图1 加入流固耦合模型的MPS法流程图
2 系泊型浮体问题的数值算法
系泊型浮体在水中运动的系统由刚性浮体、柔性绳索和水这3部分组成。本文假设绳索是极细的轻质绳索,浮体被限定在以绳索固定端为圆心、绳长为半径的圆内。不考虑绳索本身的变形,仅将绳索对刚体的作用转变为刚体运动的限制条件,从而将刚体、柔性固体和液体相互作用的复杂问题简化为刚体在液体中做运动范围受限的运动问题。
绳索具有独特的力学特性:①抗拉伸,当绳索被拉紧时,绳索内将被动地产生作用力,本文假设这一过程所需的时间非常短暂且绳索没有弹性,不会伸长,也不会发生断裂;②不抗压缩,当绳索松弛时,其内部不产生作用力,自由端可以自由运动。相应地,系泊型浮体在运动中会出现4种状态:绳索保持松弛(状态Ⅰ)、绳索由松弛变为绷紧(状态Ⅱ)、绳索保持绷紧(状态Ⅲ)和绳索由绷紧变为松弛(状态Ⅳ)。
2.1 坐标系布置
如图2所示,定义3个坐标系:①绝对坐标系oxy,所有粒子的坐标和速度均在绝对坐标系下表示;②以绳索固定端为原点的坐标系o′x′y′,用来记录连接浮体的绳索自由端的运动;③固连在浮体上的相对坐标系o″x″y″,用来记录代表浮体的固体粒子相对于基点o″的运动。
根据刚体动力学理论,刚体的平面运动可以看作是平动和转动的合成运动。其中,刚体随基点的平动部分与基点的选择有关,相对基点的转动部分与基点的选择无关。由于浮体上与绳索的连接点是一个特征位置,故将其选为基点,即平动系o″x″y″的原点。相应地,在应用式(8)~(11)时需要将下标c表示的量定义为o″的相应值,rral定义为固体粒子相对于o″的坐标。
o″(xc,yc)在坐标系o′x′y′中的坐标为(xc′,yc′),其到o′点的距离r表示绳索两端连线的长度,φ表示连线与o′x′轴正向的夹角。
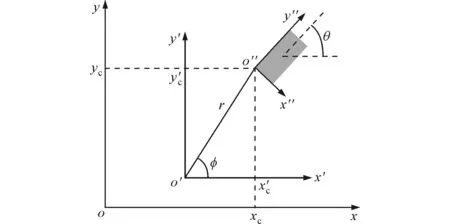
图2 坐标系设置
2.2 刚体运动状态判定机制
由于系泊型浮体的运动存在4种状态,因此计算中需要引入刚体运动状态判定机制。如图3所示,固体粒子和流体粒子一起参与压力求解,液体粒子直接根据压力梯度修正速度和坐标。对于浮体,求解刚体运动的动量方程可以得到o″点坐标和速度的估算值,由于o″固连在绳索的自由端上,r的估算值可由o″到o′的距离求得。此时,比较r值和绳长l的大小,再结合上一时间步n内浮体的状态,就可以得到下一时间步n+1内的浮体状态,具体判断结果如表1所示。例如,n时间步内浮体处于状态Ⅰ,即绳索保持松弛,而在n+1时间步中r的估算值大于l,则可判定n+1时间步的浮体应处于状态Ⅱ,即绳索由松弛变为绷紧。

表1 n+1时间步浮体状态的判定结果
若r不大于l,则表明绳索处于松弛状态,绳内无作用力,固体粒子按式(10)、(11)更新坐标和速度。若r大于l,则表明绳索已处于绷紧状态,o″只能在以o′为圆心、以l为半径的圆周上运动。因此,消除浮体速度估算值的径向部分,保留切向部分得到o″绕o′旋转的角速度ωo″,并以此修正o″的坐标
(12)

图3 加入刚体运动状态判定机制的MPS法流程图
式中:e是o′o″连线的方向向量。最后,按式(10)、(11)更新每个固体粒子的坐标和速度。
3 算 例
利用上述算法对由单根绳索系泊的浮体在孤立波中的运动响应进行了数值模拟,算例的几何布置如图4所示:宽500 mm的二维水槽中盛有100 mm深的水;左端水面上设置了一段宽120 mm、高100 mm的液柱,其倒塌后将产生一个孤立波;一个宽20 mm、高40 mm的刚性浮体淹没于水中,其左端距水槽左端240 mm,底部距水槽底20 mm,浮体密度是水的一半;浮体由一根长340 mm的细绳系泊,绳的固定端固定在水槽的左下角,自由端固连在浮体的右下角;初始时刻绳处于松弛状态,开始运动后绳索将浮体限制在双点划线的范围内。
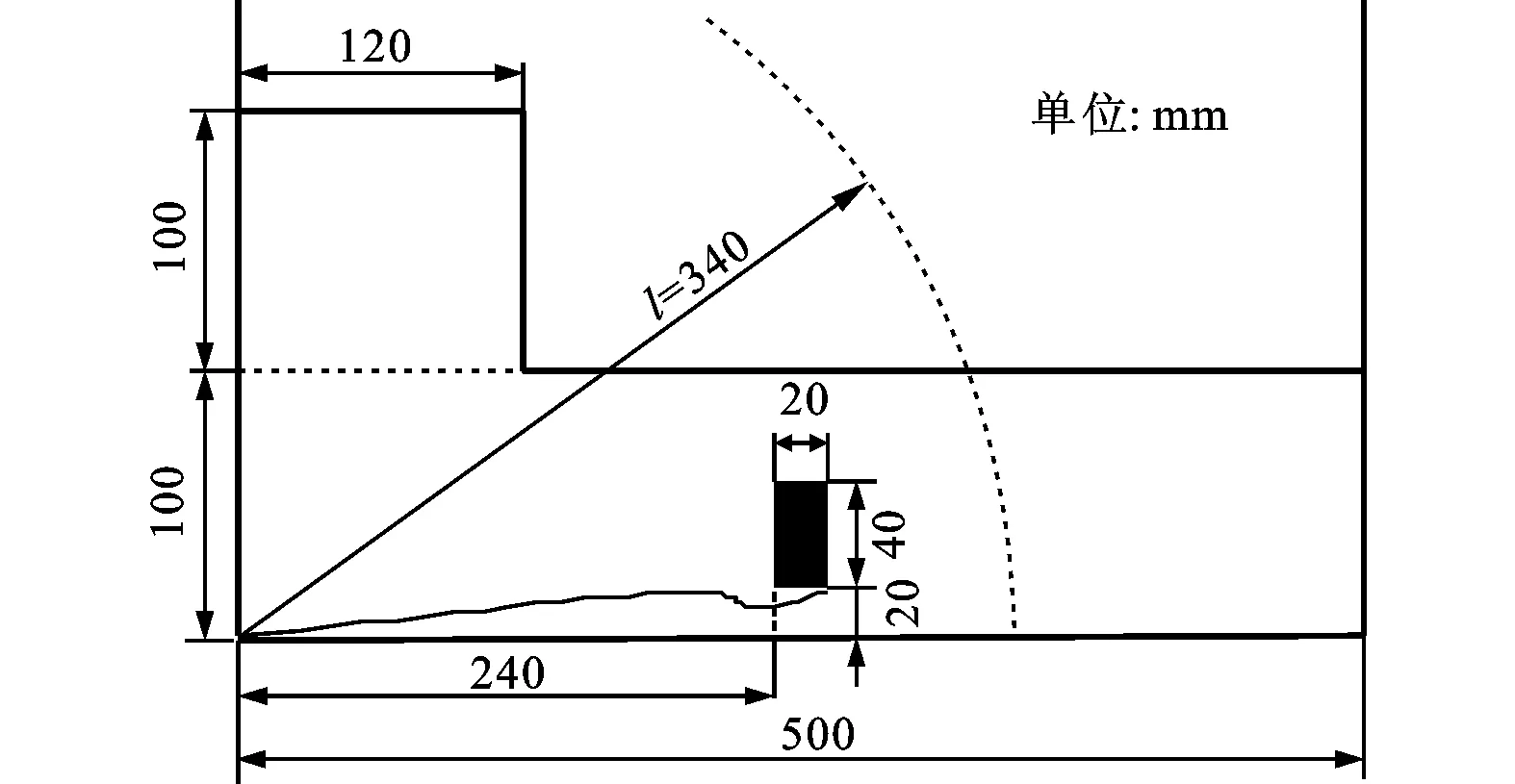
图4 几何布置示意图
如图5所示,追踪o″的坐标可以得到浮体的运动轨迹,颜色由深及浅表示时间推进。由图5可以看到,右侧有一段圆弧,表明绳索在此阶段处于绷紧状态,浮体上o″被严格限制在圆周上运动。如图6所示,监测r随时间t的变化,可以具体判断绳索处于松弛或绷紧状态。

图5 基点o″的移动轨迹

图6 r随时间t的变化
结合图5和图6,可以得到浮体运动的不同阶段:①初始时刻r=260.77 mm,绳索松弛,随着左端液柱发生溃坝并向右推进,浮体在水流的带动下向右漂动并在浮力的作用下向上浮起,r逐渐增大但不超过l,此时浮体处于状态Ⅰ,取t1=0.1 s作为特征时间;②直到t2=0.294 s,r增大到l=340 mm,绳中产生作用力,限制浮体不再在径向向外运动,此时浮体处于状态Ⅱ;③水流带动浮体继续向右运动,但由于绳索的限制,所以浮体只能绕绳索固定端旋转,绳索一直保持绷紧,浮体处于状态Ⅲ,取t3=0.4 s作为特征时间;④t4=0.521 s时,水流撞击到水槽右壁面并向左回流,带动浮体向左漂动,绳索转变为松弛状态,此时浮体处于状态Ⅳ;⑤水流来回振荡并不断撞击水槽左、右壁面,浮体运动也表现为在小范围内摇摆,但r始终没有达到l,绳索一直处于松弛状态,浮体处于状态Ⅰ,取t5=1 s作为特征时间。到15 s时,浮体只作微小幅度的摇摆,计算到此截止。
提取t1、t2、t3、t4和t5这5个特征时刻的浮体位置如图7所示,图中的波面形状对应t2=0.294 s,双点划线是浮体在绳索限制下的最大运动范围。浮体在t2和t4之间保持绷紧,o″在这段时间内一直在最大运动范围的圆周上运动,由此可证明本文提出的方法是有效且正确的。

图7 t2=0.294 s时的波面形状及4种状态下的浮体
如图2所示,定义浮体长边与水平面的夹角为θ。结合图7和图5可以看出,θ和绳索两端连线与水平面的夹角φ在运动过程中一直在不同步地变化,具体变化趋势如图8所示。初始位置φ=23.6°,浮体长边竖直,θ=90°。到15 s运动趋于停止时,φ稳定在23.6°附近,θ稳定在0°附近,此时浮体长边保持水平。

图8 φ和θ随时间t的变化
4 结 论
将系泊型浮体在液体中的运动分为绳索保持松弛、由松弛变绷紧、保持绷紧和由绷紧变松弛等4个状态,在MPS法框架下提出了一种刚体运动状态判定机制,实现了对水流和绳索双重作用下的浮体运动的数值模拟。当判定绳索处于绷紧状态时,采用消除平动速度径向分量的方法修正浮体速度,从而将刚性浮体、柔性绳索和水的相互作用问题简化为刚体在液体中做运动范围受限的运动问题求解。通过对单绳系泊的轻质浮体在溃坝产生的孤立波中的运动响应做详细的数值模拟,清晰地捕捉到了4种状态下的浮体运动。最终浮体长边稳定在水平方向,也从物理现象上证明了本文算法的正确性。
[1] LEE B H, PARK J C, KIM M H, et al. Numerical simulation of impact loads using a particle method [J]. Ocean Engineering, 2010, 37(2/3): 164-173.
[2] BOGNER S, RUEDE U. Simulation of floating bodies with the lattice Boltzmann method [J]. Computers and Mathematics with Applications, 2013, 65(6): 901-913.
[3] OMIDVAR P, STANSBY P K, ROGERS B D. SPH for 3D floating bodies using variable mass particle distribution [J]. International Journal for Numerical Methods in Fluids, 2013, 72(4): 427-452.
[4] MAYS T W, PLAUT R H, LIAPIS S I. Three-dimensional analysis of submerged, moored, horizontal, rigid cylinders used as breakwaters [J]. Ocean Engineering, 1999, 26(12): 1311-1333.
[5] DIAMANTOULAKI I, ANGELIDES D. Modeling of cable-moored floating breakwaters connected with hinges [J]. Engineering Structures, 2011, 33(5): 1536-1552.
[6] PENG W, LEE K H, SHIN S H, et al. Numerical simulation of interactions between water waves and inclined-moored submerged floating breakwaters [J]. Coastal Engineering, 2013, 82: 76-87.
[7] FERRERAS J, PENA E, LOPEZ A, et al. Structural performance of a floating breakwater for different mooring line typologies [J]. Journal of Waterway Port Coastal and Ocean Engineering, 2014, 140(3): 04014007.
[8] KOSHIZUKA S, OKA Y. Moving-particle semi-implicit method for fragmentation of incompressible fluid [J]. Nuclear Science and Engineering, 1996, 123(3): 421-434.
[9] 张帅, 解利军, 郑耀. 一种稳定的移动粒子半隐式法 [J]. 水动力学研究与进展, 2010, 25(2): 239-246. ZHANG Shuai, XIE Lijun, ZHENG Yao. A stable moving particle semi-implicit method [J]. Chinese Journal of Hydrodynamics, 2010, 25(2): 239-246.
[10]CHEN Xiao, XI Guang, SUN Zhongguo. Improving stability of MPS method by a computational scheme based on conceptual particles [J]. Computer Methods in Applied Mechanics and Engineering, 2014, 278: 254-271.
[11]钟道彤, 刘继平, 严俊杰, 等. 基于MPS方法的汽泡凝结数值模拟研究 [J]. 工程热物理学报, 2011, 32(9): 1505-1508. CHONG Daotong, LIU Jiping, YAN Junjie, et al. Numerical simulation on steam bubble condensation based on MPS method [J]. Journal of Engineering Thermophysics, 2011, 32(9): 1505-1508.
[12]PAN Xujie, ZHANG Huaixin, LU Yuntao. Numerical simulation of viscous liquid sloshing by moving-particle semi-implicit method [J]. Journal of Marine Science and Application, 2008, 7(3): 184-189.
[13]曹文瑾, 孙中国, 席光. 移动粒子半隐式法流固耦合模型及自由浮体数值研究 [J]. 西安交通大学学报, 2014, 48(8): 136-140. CAO Wenjin, SUN Zhongguo, XI Guang. Fluid-structure interaction models in mps method and its numerical simulation for floating bodies [J]. Journal if Xi’an Jiaotong University, 2014, 48(8): 136-140.
(编辑 荆树蓉)
Numerical Models of Moored Floating Bodies Using Meshless Method
CAO Wenjin,SUN Zhongguo,XI Guang
(School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China)
Four states may appear during a moored floating body’s movement (the rope keeps strained, strained first and then slaked, keeps slacked, slacked first and then strained). Based on the moving particle semi-implicit (MPS) method and combined with fluid-structure interaction model, a method to judge the floating body’s state is put forward. To simulate the movement of a moored floating body when the rope is strained, a new treatment is introduced. First, calculate the external forces applied by fluid and gravity and their torques using volume integration model and then the estimated value of the velocity and angular velocity of the floating body can be obtained by solving the momentum equation and angular momentum equation. Due to the pulling force applied by the rope in radial direction, the radial component of the estimated velocity is eliminated. The floating body rotates around the fixed end of the rope at a speed equal to the tangential component of the estimated velocity. Utilizing this algorithm, the dynamic response to the movement of a 2-D floating body moored by a single rope in a solitary wave is simulated, and the four states previously mentioned are captured. The trace of the joint point of the rope and floating body during the period when the rope keeps strained is an arc. The data including the movements in the horizontal, vertical and rotation directions can be gained from the calculation. The results agree well with the physical principle. It appears that our finding not only extends the application scope of MPS method, but also provides a new train of thought in simulating the fluid-structure interaction problems of solid bodies whose movement is limited.
moored; floating body; moving particle semi-implicit method; fluid-structure interaction
2014-07-29。 作者简介:曹文瑾(1992—),男,硕士生;席光(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(51106125,51236006);中央高校基本科研业务费专项资金资助项目(2014jdhz41)。
时间: 2014-12-18
网络出版地址: http:∥www.cnki.net/kcms/detail/61.1069.T.20141218.1008.002.html
10.7652/xjtuxb201503011
O351.2
A
0253-987X(2015)03-0062-05
