基于Autocad地形图坐标转换系统研究

2015-03-14王义

铁道勘察 2015年2期

关键词：子午线椭球高斯

王　义

(中铁二院工程集团有限责任公司，四川成都　610031)

Research on Autocad Based on Topographic Map Coordinate System Conversion

WANG Yi

基于Autocad地形图坐标转换系统研究

王义

(中铁二院工程集团有限责任公司，四川成都610031)

Research on Autocad Based on Topographic Map Coordinate System Conversion

WANG Yi

摘要介绍同椭球和不同椭球的地形图坐标转换方法，并基于Autocad平台，利用ObjectARX工具开发地形图坐标转换系统，应用于多个高铁项目，取得了较好的效果。

关键词高斯投影四参数七参数ObjectARX坐标转换

1概述

随着我国高铁技术的迅速发展，铁路勘察设计标准更加规范，对铁路设计各环节的精度要求不断提高。为了减少长距离铁路全线制图带来的投影变形误差，铁路勘察设计中必须针对铁路全线进行多个投影分带，以便更好的控制投影变形，提高铁路勘察设计精度。伴随投影分带的不断细化，带来了大量的地形图坐标转换工作。

详细介绍两种地形图坐标转换方法，一是同椭球下高斯投影正反算坐标换带法，二是不同坐标系下通过公共点解算四参数、七参数转换法。在此基础上，首次将高斯投影正反算、四参数、七参数公式引入AutoCAD平台，利用ObjectARX工具开发了地形图坐标转换软件，保证了换带精度，提高了作业效率。

2数字地形图坐标转换方法

常用的地形图坐标转换方法有两种，同椭球高斯投影正反算法及不同椭球四参数、七参数转换法。

2.1　同椭球高斯投影正反算法

为了限制长度变形，以中央子午线进行分带，把投影范围限制在中央子午线东、西两侧一定的范围内，使得统一的坐标系分割成各带的独立坐标系。在工程应用中，往往要用到相邻带中的点坐标，这样便涉及到换带计算。

地形图转换前后的坐标系如果是基于同椭球的，并且投影方式相同，可直接采用投影换带计算，投影方式较常用的有高斯投影、UTM投影及兰勃特投影等。高斯投影正算公式为

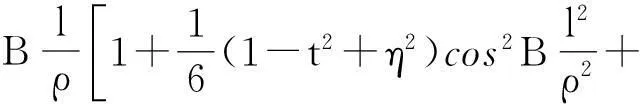
(1)

高斯投影反算公式为

(2)

式中ηf、tf分别为按Bf值计算的相应量。

a为椭球长半轴，带高程抵偿面时：长半轴=长半轴理论值+高程抵偿面高程值。为消除长度变形误差，通常做法是选择合适的基准投影面以使综合变形在容许变形范围之内，这个基准投影面我们称之为抵偿高程面。

b为椭球短半轴，f为椭球扁率，X为子午线弧长，Bf为底点纬度，带有高程抵偿面的解算，在具有高程抵偿面进行高斯变换时，应该将纬度B的差值代入

ΔB=sin2B(1-e2sin2B)Z0f/((a+Z0)(1-e2))，

式中，Z0为高程抵偿面的高程。

2.2　不同椭球四参数、七参数转换法

地形图转换前后的坐标系如果是基于不同的椭球，需要利用公共点在两个坐标系下不同的坐标值计算四参数、七参数，通过这些参数计算每个实体转换后的坐标，修改实体坐标为转换后坐标，完成不同椭球下地形图的转换工作。

四参数转换法公式为

(3)

式(3)中，x2，y2为转换后的平面直角坐标，x1，y1为原坐标系下平面直角坐标，坐标单位为m。x0，y0为平移参数，α为旋转参数，m为尺度参数。解算这4个参数，需要两个以上公共点。

七参数转换法公式为

(4)

3地形图坐标转转换系统的设计与实现

为了提高坐标转换自动化程度，同时减少人工转换可能出现的差错，根据实际情况，引用不同的转换模型，利用ObjectARX工具，采用点对点转换方法，即遍历整个AutoCAD文件中的实体，对单个实体定位点坐标进行转换计算，然后修改单个实体定位点的坐标为变换后的坐标，开发了数字地形图坐标转换软件。该软件基于AutoCAD平台底层开发，程序运行稳定，转换速度快，可实现海量数据批量转换。

基于相同椭球转换时，可查阅1954北京椭球、1980西安椭球、WGS84椭球、国家2000椭球等通用椭球，或自定义椭球的长、短半轴，椭球扁率参数，代入公式(1)、(2)，可实现任意中央子午线、任意高程抵偿面间的高精度转换。数字地形图坐标转换软件能实现自动转换，开发环境采用ObjectARX2008与VS2005，同椭球坐标转换流程如图1所示。

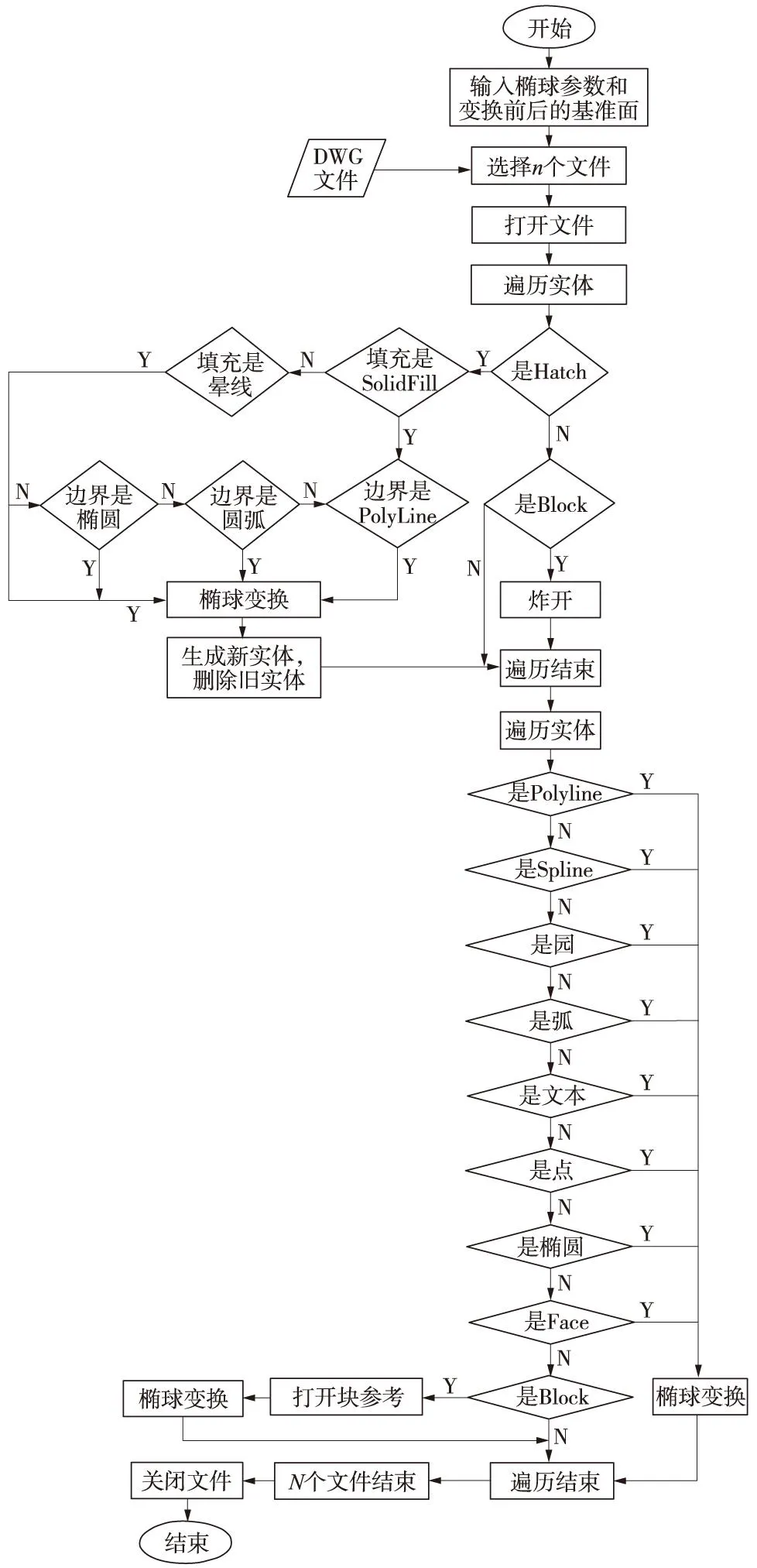
图1　同椭球坐标转换流程

基于不同椭球或者任意坐标系的转换，四、七参数转换法都可以实现，但考虑地形图转换要保证高程值不改变，四参数转换法更具有实际意义，带有高程的坐标文本文件转换可采用七参数转换法。四参数转换流程如图2所示。

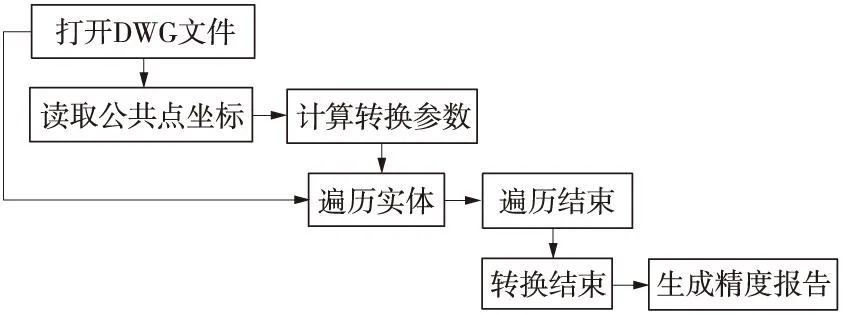
图2　四参数坐标转换流程

程序同时提供转换精度报告，即每个公共点的改正量，改正量如异常，检查公共点输入格式及判断粗差点，剔除粗差点，再进行参数计算，完成地形图坐标系转换。

对图形文件进行转换时，根据实体类型的不同，做出相应的转化。例如，针对图案填充实体可转换其边界，删除原有图案填充，依据新边界重新填充图案；坐标范围较大的块(Block)及嵌套块，如果直接转换误差会比较大，对于这种块程序采取打散后转换；文字注记、高程点及植被符号以插入点坐标进行转换；圆弧曲线转换起始点、终止点及中心点坐标，然后重新生成圆弧曲线；标注实体按标注线和标注文本分开转换；通过以上手段解决了难以转换的实体，保证换带无遗漏。

在实际项目中，会同时涉及到同椭球和不同椭球的转换，为了保证转换精度，经常综合运用高斯正反算法及四参数法。

下面以一个实例来阐述地形图换带流程。某项目地形图为北京54椭球，中央子午线经度100.5°，高程抵偿面大地高1 020 m；转换到WGS84椭球，中央子午线经度101.75°，高程抵偿面大地高为1 060 m。可先利用高斯反算模块将地形图及公共点转换到相同中央子午线，再利用四参数模块进行转换，这样，公共点投影到相同中央子午线，四参数转换残差最小，精度最高。最后在同椭球下，利用高斯正算模块将地形图转换到对应的工程独立坐标系。图3为详细的换带流程。

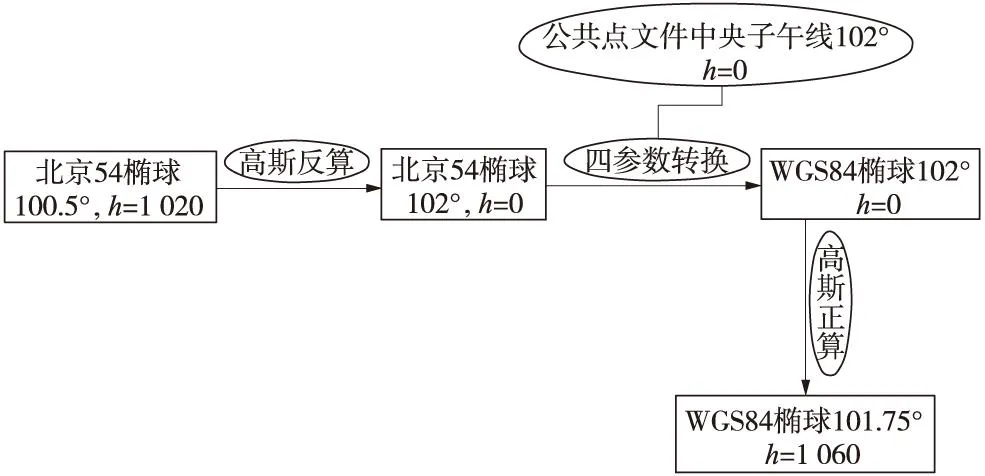
图3　地形图换带流程

4转换精度检核

4.1　同椭球换带精度检查

随机抽取某幅地形图内26个实体坐标，转换前坐标系采用WGS84椭球，中央子午线经度为103.25°，高程抵偿面大地高为1940 m；转换后坐标系采用WGS84椭球，中央子午线经度为106.5°，高程抵偿面大地高为1 255 m。通过本软件计算和西南交大的GPS2005软件计算，比较计算结果，其差值如表1。

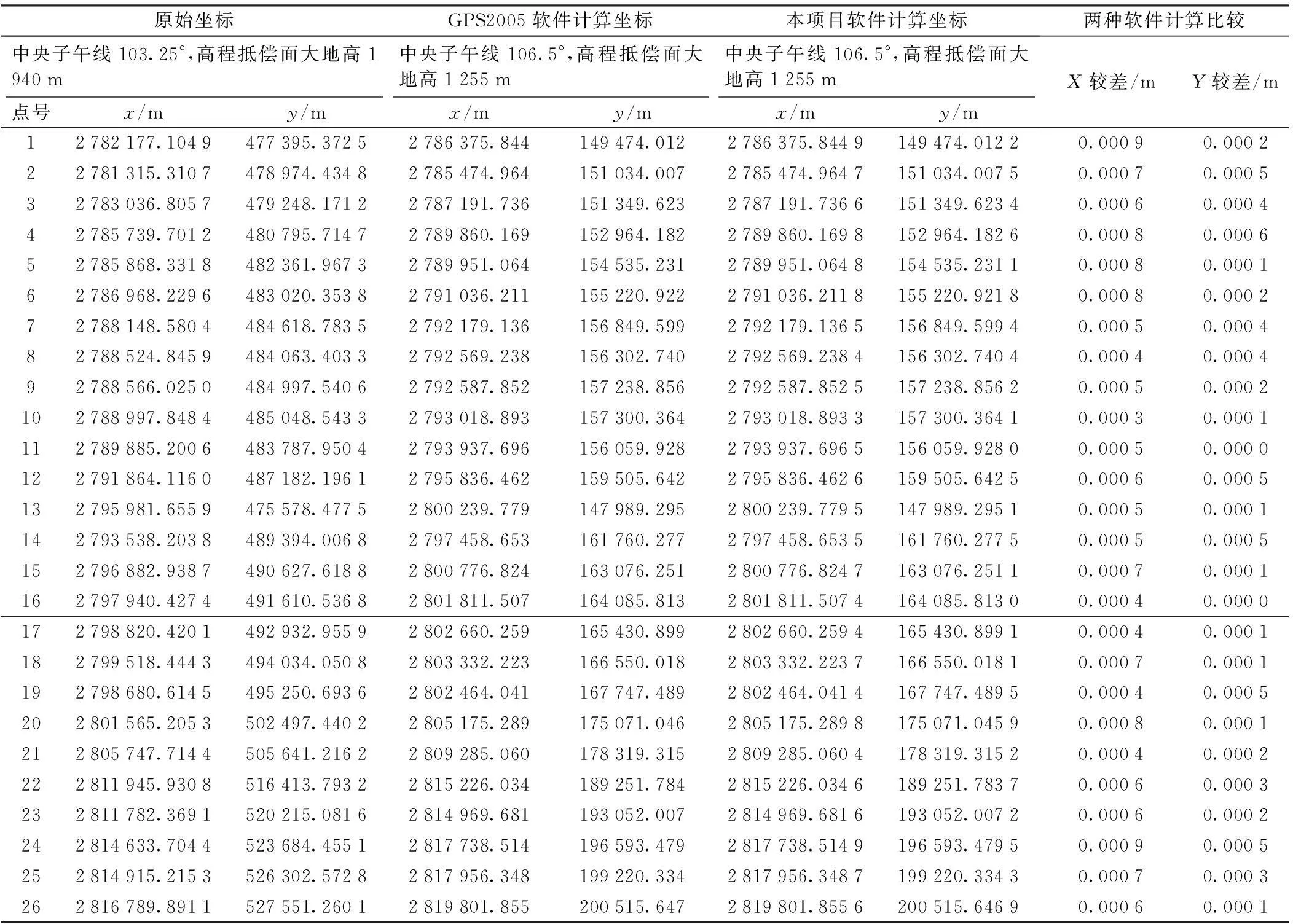
表1　同椭球换带残差比较

4.2　参数换带精度检查

实验数据为机载Lidar点云数据，原始坐标系采用Clarke 1880(克拉克)椭球，中央子午线39°，高程抵偿面大地高为0 m，投影方式为UTM投影；换带后的坐标系采用WGS84椭球，中央子午线39°，高程抵偿面大地高为0 m，投影方式为高斯投影；经分析前后坐标系为不同椭球，只能利用公共点进行转换，通过本软件选择四参数法计算和Cosawin(科傻)软件选择赫尔默特法计算，比较计算结果，其差值如表2。

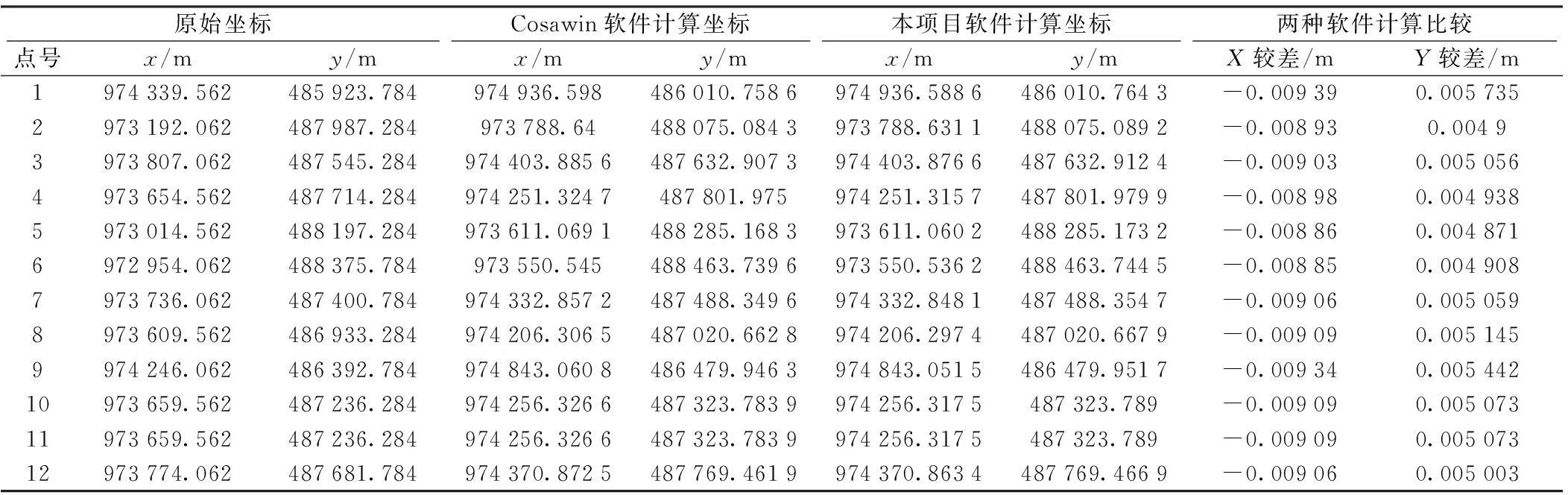
表2　参数换带残差比较

从表2统计可见，同椭球高斯正反算转换法精度优于0.1 mm，不同椭球参数转换法精度可控，与公共点精度相关。

通过多个项目验证得知，高斯投影正反算法，转换公式严密，换带精度较高。精度不受长距离、中央子午线经度跨度较大的影响。四参数、七参数转换方法，通过公共点计算平移、旋转以及缩放参数，近似实现两个坐标系的转换。该方法对于短距离、中央子午线经度跨度不大的情况，转换方法严密有效。但对于长距离、中央子午线经度跨度较大时，转换精度较差。

5结论

为了解决海量数字地形图基于多个投影分带的换带问题，探索将大地测量学数学模型引入AutoCAD平台，结合ObjectARX工具开发的地形图转换软件，实现了高精度、无遗漏及快速批量转换数字地形图功能，经过多个高铁项目实践验证，转换精度可靠，具有较强的实用性。

参考文献

[1]周适.七参数坐标转换研究及应用[J].铁道勘察，2013(5)

[2]杨锋，林春峰，程昂.基于ObjectArx地形图数据标准统一软件的设计与实现[J].铁道勘察，2014(5)

[3]梅熙.高速铁路坐标转换方法探讨[J].高速铁路技术，2012(8)

[4]管建华.基于ObjectARX的空间数据坐标变换及应用[J].现代测绘，2007(1)

[5]郑敏辉,林铁.数字地形图坐标转换工具的设计与实现[J].测绘技术装备，2008(1)

[6]刘秀军,孙小英,袁月欣.省区矢量数字地图WGS-84坐标系与1980西安坐标系的转换[J].测绘，2011(6)

[7]孔祥元,郭际明,刘宗泉.大地测量学基础[M].武汉：武汉大学出版社，2001

[8]吕忠刚,许世宁.关于抵偿高程面与移动中央子午线最佳选取问题的研究[J].东北测绘，2002(2)

[9]王小华,程传录,范宏涛，等.基于AutoCAD.NET API的地形图坐标转换实现方法研究[J].测绘与空间地理信息，2013(11)