多重不确定下生产与运输的联合优化模型

牟德一，常小定

（中国民航大学理学院，天津 300300）

多重不确定下生产与运输的联合优化模型

牟德一，常小定

（中国民航大学理学院，天津 300300）

考虑如何根据不同的运输需求来组织对所需产品的生产,使得生产和运输总成本最小。在假设需求量为随机变量的条件下,生产厂家生产单位产品所需的成本和所消耗的原材料为不确定变量,从而建立了生产运输的不确定随机规划模型。最后,一个实例表明了所建立的模型是有效的。

生产管理;运输问题;不确定变量;不确定随机规划

对于生产企业来说，生产问题和运输问题是很重要的问题，通常这两个问题被单独考虑。然而为了寻求利益的最大化，企业不得不考虑生产与运输的整个过程，不仅要安排合理的生产计划，还要规划出相应的运输方案。因此，许多研究者开始综合考虑生产与运输，优化生产-运输系统的问题。Glover，Jones，and Karney（1979）以供应链管理（SCM）的形式提出了生产-分配-库存的规划系统（PDI）[1]；Blumenfeld，Burns，and Daganzo（1991）建立了生产和运输的整合模型[2]；Holmberg and Tuy（1999）假设需求为随机变量，研究并提出了具有随机需求和凹生产成本函数的生产-运输模型[3]。然而，这些模型都直接或间接地与库存相联系，其中库存成本占据着总成本中相当大的部分。显然，为了降低成本，有必要建立直接的生产-运输模型，以寻求利益的最大化。

另一方面，在实际的生产-运输过程中，由于原材料的缺乏、市场情况的变化、天气以及道路条件的变化等诸多因素，使得原材料的供应量、生产和运输成本、需求量等成为不确定变量。为了处理这种不确定性，Liu（2007）提出了不确定理论，随后，将不确定理论应用于生产和生活实践之中，提出不确定规划[4]，建立不确定模型；并在2013年重新补充和修订了这一理论[5]。于是，更多的研究者开始从事这一领域的研究工作。基于这一不确定规划，Rong（2011）提出了两个具有不确定成本的不确定库存模型[6]；Mou等（2013）建立了最小化运输时间的运输模型[7]；Gao（2012）研究了不确定设备选址问题[8]。但到目前为止，尚未见到利用不确定理论研究生产和运输联合决策问题的报告。在实际的生产-运输的过程中，产品与原料信息数据往往相对缺乏，此时需利用专家意见来综合出相关量的不确定性度量，而不确定理论提供了此类问题的建模工具。

基于以上考虑，本文将利用不确定规划研究生产-运输问题。在最优化生产和运输的操作过程中，不仅要使原材料得到充分利用，而且还要使得运输需求得到尽可能的满足。于是，在生产过程中运用不确定机会约束，而在运输过程中利用随机机会约束，建立生产运输的不确定-随机的联合优化模型，并研究此模型的确定性等价问题以及求解方法。最后给出一个算例。

1 基本知识

本节介绍不确定理论的一些基本知识，作为后续问题的研究基础。

定义1 从不确定空间（Γ，L，M）到实数集的可测函数ξ=ξ（r）称为不确定变量，如对任意的实数博雷尔集B，集合

是一个事件。

于是，对于一组不确定变量ξ1，ξ2，…，ξn和一实值可测函数f，有

为了进一步研究不确定变量，像概率分布那样，下面给出不确定分布的概念。

定义2 设ξ是一个不确定变量，对于任意实数x，称

为不确定变量ξ的不确定分布函数。

为了根据不确定分布计算不确定测度，Liu（2013）提出了测度反演定理。

定理1 设ξ是一个不确定变量，且有连续的不确定分布Φ，那么对任意的实数x，有

定义3 不确定分布Φ被称为是规则的，如果对每一个α∈（0，1），其逆函数Φ-1（α）都存在且唯一。

定理2 设ξ1，ξ2，…，ξn是独立的不确定变量，且分别有规则的不确定分布Φ1，Φ2，…，Φn。如果函数f（x1，x2，…，xn）对于x1，x2，…，xm是严格增的，对于xm+1，xm+2，…，xn是严格减的，那么

是一不确定变量，且有逆不确定分布

定义4 设ξ是一个不确定变量，那么ξ的期望值为

假设这两个积分中至少有一个是有限的。

定理3 设ξ是一个不确定变量，且有规则的不确定分布Φ，如果期望值存在，那么有

同时，Liu（2013）提出了期望值算子的线性性质，即

其中：ξ、η为两个独立的不确定变量且有有限的期望值；a，b为任意的两实数。

2 问题的描述及分析

生产-运输网络建模的基本目标是优化生产-运输成本，在考虑生产过程中原材料的消耗和加工的同时，还应充分把握运输过程中节约成本的机会。在生产过程中，降低生产成本的同时，必须在各自的生产能力范围之内安排自己的生产任务。在利用不同的运输工具进行运输时，单位运输成本会有所不同；因此，必须制定基于需求的运输方案，以达到减少不必要的运输和降低运输成本的目的。

本文将考虑不确定需求下的单产品生产-运输网络（多个生产商和多个客户）。根据不同的运输需求来组织对所需产品的生产，使得生产-运输总成本最小。在需求量为随机变量，生产厂家生产单位产品所需的成本和所消耗的原材料为不确定变量的条件下，利用不确定规划和随机规划方法建立了生产运输的不确定随机规划模型。

3 模型的建立

3.1 不确定的产品生产模型

假设有m个生产厂家，为n个不同的客户生产同一种产品P，P由l（l=1，2，…，k）种原材料h1，h2，…，hk加工而成。又有如下符号假设：ci0为厂家i（i=1，2，…，m）的启动成本；ηi为厂家i（i=1，2，…，m）所生产的产品P的单位可变成本，为不确定变量；ξihl为厂家i生产单位产品P所消耗的原材料hl（l=1，2，…，k）的不确定变量；φi为ηi的不确定分布；φihl为ξihl的不确定分布；Shl为原材料hl的供应量；yi为厂家i所生产的产品P的产量，为决策变量；Vi为厂家i的生产能力；αhl为预先给定的置信水平。

基于以上假设，在充分利用原材料的基础上，以最小化生产成本为目标，建立如下不确定产品生产模型为

在上述模型中，目标函数是最小化期望成本，而主约束为使得原材料得以充分利用的不确定机会约束。

3.2 随机需求的运输模型

假设n个不同的顾客对产品P的需求是随机的，且由上述m个生产厂家供应。符号假设如下：cij为从生产厂家i到顾客j的单位运输成本；xij为从生产厂家i到顾客j的运货量，为决策变量为需求量bj是服从正态分布的独立随机变量n）为预先给定的置信水平为标准正态分布函数。

根据传统的运输问题模型，带有随机需求的运输问题模型为

在此模型中，主约束使得需求得到最大程度的满足。

3.3 生产与运输的联合优化模型

生产问题与运输问题是运筹学研究的两个重要问题。当考虑由生产商加工产品，再运送到顾客的整个过程时，就需要综合考虑生产和运输两大重要问题。不同的生产计划需要安排不同的运输方案；而不同的运输需求也要求生产计划有相应的调整。因此，根据实际情况的不同以及要实现的目的的不同，设计合理的生产-运输方案将是十分必要的。

在实际生活中由于生产与运输结合的紧密性，所以为了减少生产与运输的总成本，必须综合考虑这两个问题而不是单个考虑。首先，为了达到节约成本的目的，必须有效地组织生产并安排运输。因此，在这里考虑使得每个生产商生产的产品全部得以运输，即

基于上式，可根据需求的变化来对产品的生产进行有效的调整，以达到降低各方成本、优化生产运输网络的目的。

于是联立模型（1）和（2），立即可得不确定环境下的生产运输联合优化模型为

为了求解这一模型，根据3.1节中介绍的不确定理论，可得如下引理。

引理1 假设函数g（x，ξ1，ξ2，…，ξn）对于 ξ1，ξ2，…，ξk是严格增的，对于ξk+1，ξk+2，…，ξn是严格减的。如果ξ1，ξ2，…，ξn是独立的不确定变量，且分别有不确定分布Φ1，Φ2，…，Φn，那么机会约束

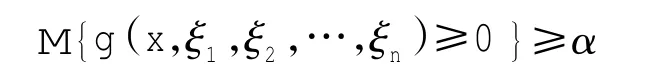
成立，当且仅当

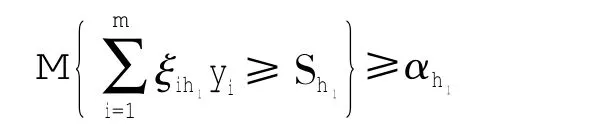
等价于

由引理1及不确定理论，有如下定理成立。

定理4 不确定机会约束

又由概率论的知识，可得如下定理。

定理5 在模型（2）中，随机机会约束

等价于

那么，基于3.1节中介绍的不确定理论及定理4、定理5，就可得到模型（3）的确定性等价模型为

这是一个线性规划模型，可用Matlab软件中的linprog命令求解。

4 数值算例

假设某产品P安排在A1、A2、A3三个产地生产，需消耗h1、h2、h3三种原材料，并分别运往四个销地B1、B2、B3、B4。又根据专家意见有：生产单位产品P需消耗原材料h1、h2、h3的量服从线性不确定分布L（ai，hm），i=1，2，3，m=1，2，3。生产产品P的单位可变成本服从ZigZag不确定分布Z（ai，bi，ci），i=1，2，3。目的地j的需求量为随机变量，服从正态分布。表1和表2给出了这些参数的值以及其他数值。

表1 生产厂家的各个参数值Tab.1 Parameters of manufacturers

另外，假设信度水平αhl= 0.9，l = 1，2，3，βj= 0.95，j=1，2，3，4。因为线性不确定变量L（a，b）的逆不确定分布为：Φ-1（α）=（1-α）a+αb，ZigZag不确定变量Z（a，b，c）的逆不确定分布为：如果α≥0.5，Φ-1（α）=（2-2α）b+（2α-1）c。又对标准正态分布有Φ-1（0.95）=1.645，因此根据模型（4），立即可得关于此生产-运输系统的优化模型为

表2 单位运输成本及需求量的正态分布参数Tab.2 Normal distribution of unit delivery cost and demand

这是一个线性规划模型，用Matlab软件中的linprog命令可得该模型的解，亦即最优生产计划、运输方案以及生产量和需求量如表3所示。

表3 最优运输方案、生产商的产量以及需求地需求量Tab.3 Optimal transportation scheme，manufacturers’outputs and destinations’demands

生产所需的成本为 302.000 0，运输成本为21.260 0，总成本为333.260 0。

5 结语

本文考虑了生产与运输的整个过程，研究了具有多生产商多目的地的单产品生产-运输问题。在生产过程中，通过引入不确定理论，提出了不确定的产品生产模型；在运输过程中，假设需求量为随机变量，建立了随机需求的运输模型。基于根据不同的运输需求来组织对所需产品的生产，使得生产运输总成本最小的生产-运输方案的考虑，假设所生产的产品能够及时全部地运送到需求地，从而联立不确定的产品生产模型和随机需求的运输模型，建立了生产-运输的联合优化模型。通过对目标函数取期望以及对约束函数取信度，将这一不确定随机的联合优化模型转化为确定性的模型。此确定性模型是一线性规划模型，可利用Matlab求解。最后，通过一个实例说明本文所建立模型和方法是有效的。

[1]GLOVER F，JONES G，KARNEY D.An integrated production，distribution，and inventory planning system[J].Interfaces，1979，9：21-35.

[2]BLUMENFELD D E，BURNS L D，DAGANZO C F.Synchronizing production and transportation schedules[J].Transportation Res，1991，Part B 25：23-37.

[3]HOLMBERG K，TUY H.A production-transportation problem with stochastic demand and concave production costs[J].Mathematical Programming，1999，85：157-179.

[4]LIUB.TheoryandPracticeofUncertainProgramming[M].2nded.Berlin：Springer-Verlag，2009.

[5]LIU B.Uncertainty Theory[M].4th ed.Berlin：Spinger-Verlag，2013.

[6]RONG L.Two new uncertainty programming models of inventory with uncertain cost[J].Journal of Information and Computational Science，2011，8（2）：208-288.

[7]MOU D Y，ZHAO W L，CHANG X D.A transportation problem with uncertain truck times and unit costs[J].Industrial Engineering And Management Systems，2013，12（1）：30-35.

[8]GAO Y.Uncertain models for single facility location problem on networks[J].Applied Mathematical Modelling，2012，36（6）：2592-2599.

（责任编辑：杨媛媛）

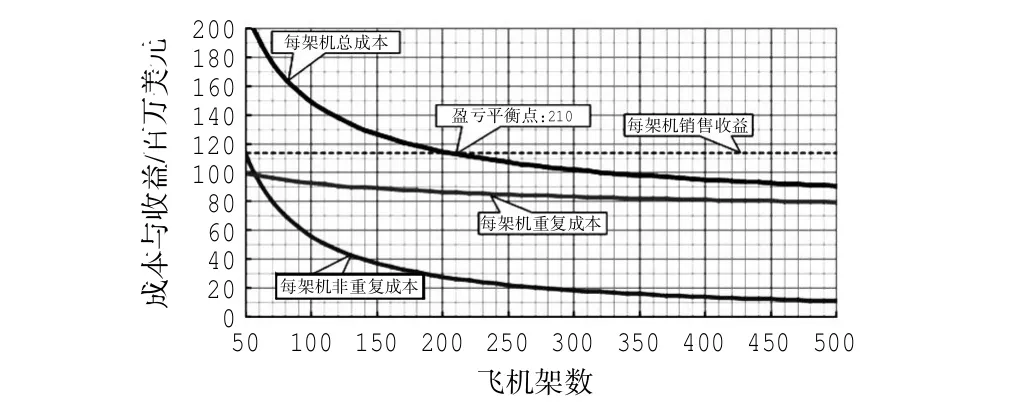
图13 盈亏平衡分析Fig.13 Breakeven analysis

本算例中的研制成本、定价和盈亏平衡点分析，是在一系列假设条件下得到的，当这些假设因素变化时，结论将随之变化。对主要影响因素讨论如下：

1）发动机和系统采购成本 每架机增加发动机和系统采购成本500万美元，盈亏平衡点为232架；

2）熟练系数 劳务成本的熟练因子b的假设，如果从0.85变为0.88，盈亏平衡点将变为243架；

3）客户服务支出 如果客户服务支出占销售收入的比例从5%升为8%，盈亏平衡点将变为228架；

4）项目研制周期 增加项目研制周期，将增加非重复成本和盈亏平衡架数。

4 结语

本文描述了民机产品的全寿命周期成本的定义与初步估算方法，以基于DOC的竞争定价为纽带，形成完整的民机项目经济可行性分析模型。通过工程实践，具有一定的实际指导意义。

当然，在国产民机型号的实际应用中还存在一些问题，主要表现在：①成本数据统计规范不能满足评估模型要求，包括研发成本统计规范和运营成本统计规范；②成本经验数据缺失和矛盾，对模型的应用提出了较大的挑战；③本模型还未考虑时间价值的因素，计算存在误差。解决上述问题，将是未来主要的研究方向。

参考文献：

[1]The Geography of Transport Systems.Development Costs for Selected Aircraft[EB/OL].[2013-10-15].http：//people.hofstra.edu/geotrans/eng/ ch3en/conc3en/table_aircraftdevcosts.html.

[2]李晓勇，宋文斌.民用飞机全寿命周期成本及经济性设计研究[J].中国民航大学学报，2012，30（2）：48-55.

[3]Cost Analysis Improvement Group，Office of the Secretary of Defense，USA，Operating And Support Cost-Estimating Guide[R].October 2007.

[4]MARKISH J.Valuation Techniques for Commercial Aircraft Program Design[R].S M Thesis，MIT，2002.

（责任编辑：黄 月）

Joint optimization model of production and transportation under multi-uncertainty

MOU De-yi，CHANG Xiao-ding
（College of Science，CAUC，Tianjin 300300，China）

Organizing the required products’manufacture according to various transporting demands can make the total cost of manufacture and transportation the least.Consuming that the delivery demands are random variables，and the cost of unit product manufacture as well as the consumed raw materials are uncertain variables，the uncertain stochastic programming model about production and transportation is developed.Finally，a practical case verifies the effectiveness of the model.

production management；transportation problem；uncertain variables；uncertain-stochastic programming

O221

:A

:1674-5590(2015)02-0060-05

2013-10-23；

:2013-11-11

:中央高校基本科研业务费专项（ZXH2012K005）

牟德一（1960—），男,四川合江人，教授，博士，研究方向为运筹与优化、航空运输管理.