基于改进免疫粒子群算法的动态航班着陆调度

冯兴杰，刘 东

（中国民航大学计算机科学与技术学院，天津 300300）

基于改进免疫粒子群算法的动态航班着陆调度

冯兴杰，刘 东

（中国民航大学计算机科学与技术学院，天津 300300）

为改进机场终端区空中交通流量管理,对动态航班着陆次序进行适当调整,使机场和空域的可用容量达到最有效利用,减少航班延误造成的经济损失,提出一种新颖的动态免疫粒子群优化算法（DIPSO）,重点针对待着陆航班的动态变化,结合滑动时间窗,多方面考虑现实约束,在确保航班延误成本最小的同时,兼顾航班着陆的公平性和管制员的工作负荷。仿真结果表明,在处理动态航班着陆问题上与先来先服务相比有效降低了延误成本。

免疫粒子群优化;航班着陆调度;动态;最小延误成本

随着世界航空运输的迅猛发展，急剧增长的空中交通需求与有限的枢纽机场空域资源间的矛盾日益尖锐，如何提高机场终端区航班调度自动化水平已成为一个亟待解决的难题。仅通过空中交通管制设施的改善已不能作为提高空中交通流量的主要方法。对跑道容量起决定性作用的因素是连续航班流之间的间隔，它与天气、导航设施、航班类型等因素密切相关。因此，合理安排不同类型航班的降落顺序，对提高机场容量、增大机场流量意义很大。

飞机着陆调度（aircraft landing scheduling，ALS）问题是具有多约束特性的典型NP难问题，国内外学者广泛研究ALS问题，提出了较多优化解决方案，但由于ALS问题本身的复杂性，至今未能得出完善的理论和方法。目前中国飞机调度基本采用先来先服务FCFS（first-come，first-served）的方式进行。该方法的不足之处是不能综合考虑飞机的多方面因素，如机型、延误成本等[1-3]。近年来，在智能优化领域寻找一种可行有效的调度方案，一直是研究的热点和难点，为解决大规模的ALS问题提供了相对可行的方法，主要包括遗传算法（genetic algorithm，GA）[4-6]、粒子群算法、禁忌搜索、模拟退火、蚁群算法等[7-8]。

本文分析了标准PSO（particleswarmoptimization）[9]算法原理，通过引入生物免疫机制思想，提出了一种新的动态免疫粒子群优化（dynamic immune particle swarm optimization，DIPSO）算法。并建立由滑动时间窗控制的动态航班优化模型，以航班总的延误成本最小为目标函数，综合考虑兼顾公平，在多种约束条件限制下，最终给出与标准粒子群、先来先服务FCFS相比具有明显优势的合理调度方案。

1 问题建模

1.1 变量描述

1）P={x1，x2，…，xn}表示动态进入终端区等待降落的航班序列；

2）Ei为航班i的最早着陆时间（i=1，2，…，n）；

3）Li为航班i的最晚着陆时间（i=1，2，…，n）；

4）Ti为航班i的最佳着陆时间（i=1，2，…，n）；

5）Si为航班i的实际着陆时间（i=1，2，…，n）；

6）TPi为航班i的机型（i=1，2，…，n）；

7）gi为航班i早于Ti着陆的单位时间成本（i= 1，2，…，n）；

8）hi为航班i晚于Ti着陆的单位时间成本（i= 1，2，…，n）；

9）αi为航班i早于Ti着陆的最大时间；

10）βi为航班i晚于Ti着陆的最大时间；

表示航班i不能在最佳着陆时间降落所造成的额外耗费成本。

各类型的航班都有最佳着陆时间（preferred time），按照此时间着陆的额外费用为0，如果航班加速提前或延迟着陆都会造成额外的费用，图1说明了某架航班在飞行中带来的额外费用变化情况。

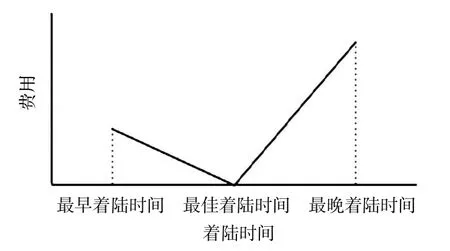
图1 航班着陆时间额外费用Fig.1 Extra cost of flight landing time

为方便计算，规定航班的机型大小S为轻型，L为中型，H为重型，各机型的额外损耗成本如表1所示。

1.2 优化目标

在安全调度的前提下以航班总额外耗费成本为首要考虑要素，有

表1 各机型消耗成本（元/min）Tab.1 Cost of various aircraft types

由于航班调度问题的目标函数越小越好，而通常的进化算法中，适应度大的个体适应性越好。因此，设计适应度函数为

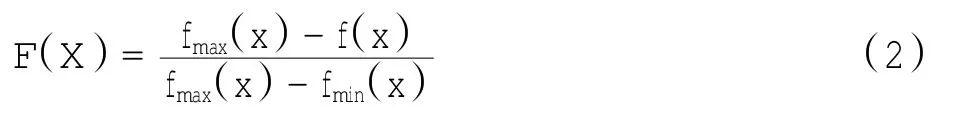
其中：fmax（x）、fmin（x）为本次迭代计算中最大、最小目标函数值。

1.3 约束条件

1）位置约束

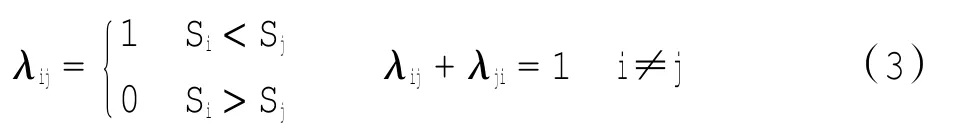
λij表示航班i与航班j的位置关系，i在j之前降落；λji表示航班j在航班i之前降落；λij=1表示航班i早于航班j降落，否则航班i晚于航班j降落。

2）安全间隔

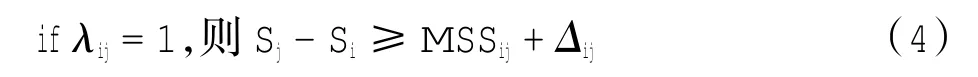
该式表示若航班i早于航班j降落，则航班i与航班j之间的间隔不小于最小安全尾流间隔加一个冗余间隔；Δij由现场管制员的经验决定，MSSij由表2确定。

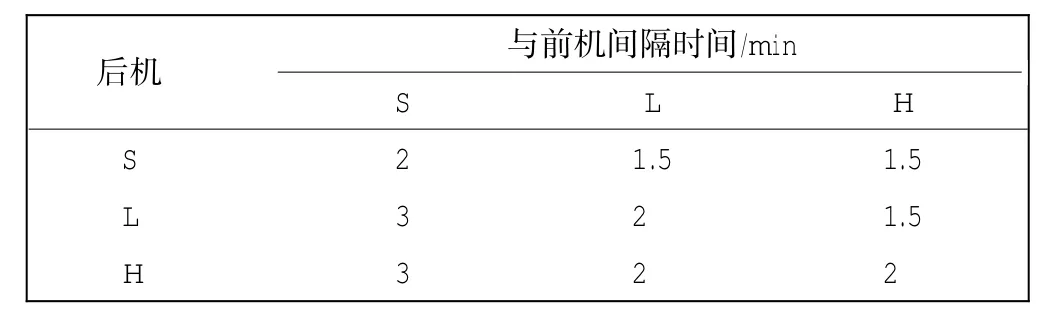
表2 最小安全尾流间隔时间Tab.2 Minimum safe turbulance seperation

3）实际着陆时间窗约束

受到航班的性能、所剩燃油的数量等因素影响，航班的实际着陆时间不能无限制提前或滞后，因此航班i的实际着陆时间为最早着陆时间和最晚着陆时间之间的离散时间段，即Ei≤Si≤Li。

4）管制员工作负荷约束

在满足安全调度的前提下，若没有较大幅度的改进，则尽可能减少航班着陆序列的变更，减少管制员的工作负荷。

5）最大位移限制

各航班的最大位移MPS=3，即每个航班提前或推后的相对位移不得超过3个以上航班。

6）航班加速限制

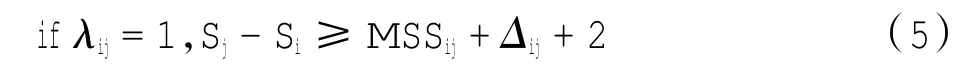
且航班j与其在一个时间片段内的航班有着陆时间冲突时，航班j加速飞行，但加速时间不超过相应安全规定。

7）同一类型的航班相对位置不发生调换

在FCFS序列中的λij值，若TPi=TPj，则在算法调整后的序列中，λij的值不发生变化。

8）间接时间窗限制

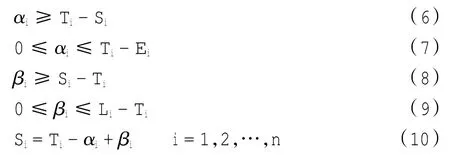
式（6）、式（7）表示航班i早于最佳着陆时间Ti着陆时，最佳着陆时间Ti与实际着陆时间Si的差值不大于αi，而αi是不大于Ti-Ei的非负值；同理，式（8）、式（9）表示航班i晚于最佳着陆时间Ti着陆时，实际着陆时间Si与最佳着陆时间Ti的差值不小于βi，而βi是不大于Li-Ti的非负值；式（10）表示航班i的实际着陆时间Si受到αi和βi的限制，向最佳着陆时间Ti靠近。

2 动态调度算法及其优化

2.1 滑动时间窗策略

就当前时间间隔，根据目前有效信息，对进入时间窗的问题通过免疫粒子群优化算法进行优化。如图2所示，时间窗开始时间为T（k）、结束时间为T（k）+ nt，这一时段就是一个滑动时间窗的长度，它由n个长度为t的时间片段组成，称为第k个滑动时间窗。利用免疫粒子群优化算法，每次优化计算一个时间窗内的航班序列，在符合约束条件的情况下只执行前5个架次航班的结果（结果不足5个时全部执行），此后将时间窗向后推进一个长度为t的时间片，否则重新计算并检验结果。重复执行上述相同优化。这样就形成一个动态效果，在有航班安排着陆的同时，又有新的航班进入终端区等待优化排序。将已经排好序列进入冻结区的航班信息删除，加入新进的航班信息，采用算法重新优化计算。

2.2 标准粒子群算法

图2 滑动时间窗优化示意图Fig.2 Optimization of sliding time window

初始化微粒为一群随机粒子（随机解），通过迭代算法找出问题的最优解或满意的解，每个个体看作N维搜索空间中的一个质点，在搜索空间中以一定的速度飞行，个体速度根据自我认知经验和群体的社会认知经验进行动态调整。第i个粒子表示为：Xi=（xi1，xi2，…，xiN），它所经历的最好位置记为pbest=（pi1，pi2，…，piN），在群体中所有微粒经历过的最好值记为gbest=（g1，g2，…，gN），微粒i的速度记为Vi=（vi1，vi2，…，viN）。每次迭代按如下公式进行速度和位置的变更，即

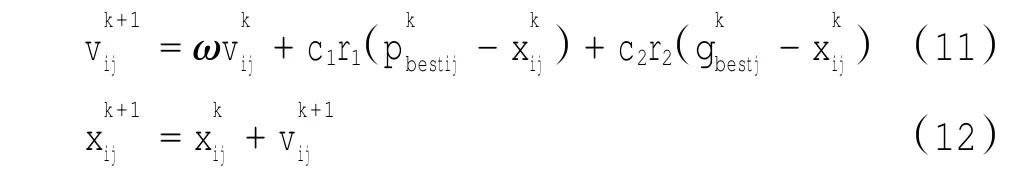
式中：ω为惯性权重，控制着上次迭代粒子的速度对本次迭代的影响；c1、c2为加速常数（accelerationconstant），也称为学习因子；r1、r2为[0，1]之间的随机数，c1r1构成的系数影响粒子从pbest获取更新信息，c2r2构成的系数影响粒子从gbest获取更新信息；1≤j≤N，k为迭代次数。

粒子的种群多样性影响全局搜索能力，分析标准PSO算法得出，在算法迭代过程中，种群多样性逐渐减小，导致出现早熟现象，同时算法收敛到一定精度，陷入局部最优，无法继续优化。为解决该问题，对标准PSO算法做以下改进：①通过PSO与免疫算法机制的结合，增加PSO粒子种群多样性；②调整惯性权重。

2.3 与免疫算法结合

免疫系统是维护生物体健康的防御系统，生物利用该系统抵抗各种病菌入侵，该系统通过识别“自我”和“异己”抗原、免疫应答排除抗原性异物，维持生理平衡。在免疫调节过程中，浓度较低且与抗原的亲和力较大的抗体将会得到促进，反之，将会受到抑制，从而保证了抗体的多样性。免疫系统将与入侵的抗原反应，部分抗体作为记忆细胞被保留，当同类抗原再次入侵时，相应的记忆细胞被激活而产生抗体[10-12]。

借鉴该思想，在优化算法中创建一个记忆库，保留历次迭代中的全局最优个体。通过浓度选择和粒子更新，替换掉种群每代进化中的较差个体，提高算法种群多样性，较大程度上降低算法陷入局部最优的可能。粒子浓度选择公式为

结合免疫思想的改进粒子群算法在航班着陆调度中的实现步骤如下：

1）检查是否有特殊航班需要及时安排着陆，若有则优先调度。

2）设定滑动时间窗的相应参数。

3）读取当前时间窗内的航班信息。

4）确定参数值：学习因子c1和c2，种群规模为N，粒子（抗体）维度为n，最大迭代次数为runmax，免疫记忆库的记忆粒子个数为m。

5）初始化：随机产生N个粒子Xi及“飞行”速度Vi，Xi为待着陆航班的随机排列，Vi为随机产生的调整序，含1个调整因子，将粒子i的初始化位置记为历史最优位置pbesti，i=1，2，…，N，将初始化中位置整体最优的粒子记为全局最优gbest，形成初始粒子种群S0。

6）迭代计算形成免疫记忆库：为减小管制员的工作负荷，使调整后的航班序列与FCFS序列尽量一致，将FCFS序列作为免疫记忆库中的常驻粒子。由式（11）、式（12）迭代计算，每次迭代将各粒子的迭代结果与当前的pbesti进行适应度值比较，若比当前pbesti优，则用本次迭代结果替换当前pbesti；同理选出适应度值最大的粒子和当前全局最优粒子gbest比较，如果较优，则将其作为全局最优粒子，更新全局最优位置gbest，并将其加入到免疫记忆库中，如果记忆库已满，则将该粒子替换记忆库中除FCFS序列以外的适应度最差粒子。

7）粒子库的生成：①由粒子群优化算法速度和位置的更新产生N个粒子；②随机产生M个新粒子。

8）粒子浓度选择：用浓度选择式（13）计算步骤4）中生成的N+M个粒子的选择概率，根据大小选择N个粒子形成种群。

9）粒子更新：用记忆库中的m个粒子替换步骤5）中得到的N个粒子中适应度较差的m个粒子，得到更新后的种群Sk+1。

10）迭代终止判断：若达到最大迭代次数，或者相邻两次迭代结果误差绝对值小于ε=0.001，则终止迭代，否则转步骤3）。

11）对上面提供的结果进行检验，若满足章节1.3中的8个约束条件，则执行前5个航班，不足5个则全部执行。其他航班进入下一个时间窗。否则放弃本次结果，重新计算。

12）判断航班调度是否完毕，若完毕，则结束运算，否则，将时间窗向后滑动一个时间片段，如图2所示，并返回步骤3）。

在免疫粒子群（DIPSO）算法基础上，航班着陆调度流程如图3所示。

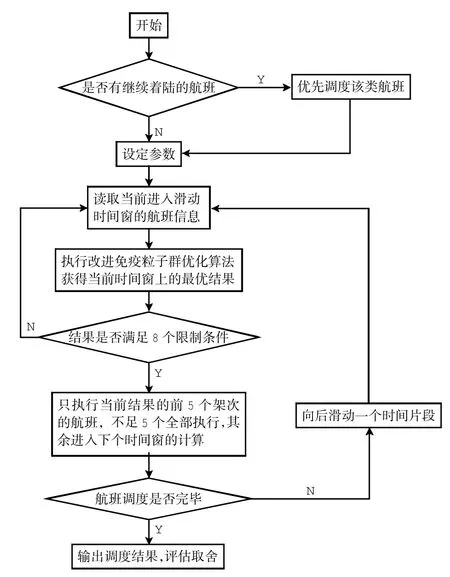
图3 航班着陆调度流程图Fig.3 Scheduling flowchart of flight landing

2.4 改进粒子群算法系数

为避免算法过早收敛并加快收敛速度，Shi等[13]提出了惯性权重的方法，惯性权重决定了对粒子当前速度的继承，较大的惯性权重将使粒子具有较大的速度，从而具有较强的全局探索能力；较小的惯性权重将使粒子具有较强的局部开发能力。在标准粒子群中惯性权重是线性减小的，即

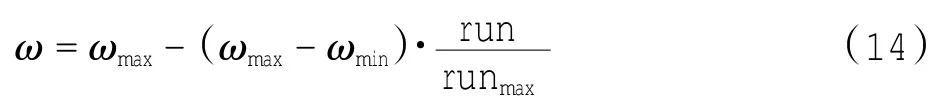
其中：ωmax为最大惯性权重；ωmin为最小惯性权重；run、runmax分别为当前迭代次数和最大迭代次数。但对于一些较为复杂的非线性问题，ω的变化并非都是线性的，找到一种针对解具体问题的曲线变化，对算法的改进至关重要。

就航班着陆排序问题，通过理论和实验的共同研究得出较大的惯性权重ω，能够使得粒子群算法有着较强的全局搜索能力，从而搜索较大的区域，便于更好地确定最优解的大概位置；而较小的ω则使得算法具有更强的局部搜索能力，即小的ω使得PSO算法的速度变化减慢，在局部小范围中能够进行精细的搜索，如此便能更好地确定最优解。对于不同的复杂优化问题，都有着与各自问题相适应的惯性权重ω变化曲线。本文针对航班着陆调度优化问题就PSO算法中ω的变化参考了文献[14]，结合团队合作精神，即利用多条曲线减小函数，产生一组由大到小的变化曲线，根据这组曲线函数制定了一组ω，就航班着陆调度的同一数据进行了多次重复试验。经实验结果对比，不同ω所得结果都有差别，结合航班着陆调度问题的综合考虑，最后对惯性权重ω做出以下改进，即

同理学习因子c1、c2对继承个体最优和全局最优起着很大作用，c1越大，则受个体最优的影响越大，反之越小；c2越大，则受全局最优的影响越大，反之越小；算法开始迭代时，个体最优有利于全局搜索，迭代后期全局最优有利于局部搜索，所以个体最优和全局最优呈反比趋势更有利于算法搜索最优值，因此本文对学习因子c1、c2也做了相应的改进，即

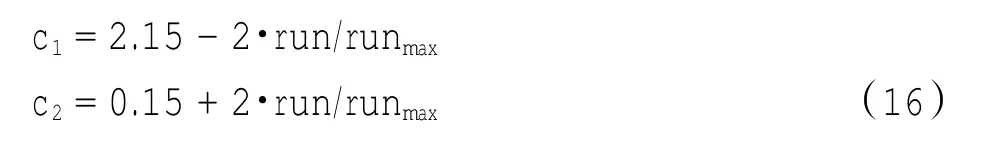
实验数据证明，本文的改进取得了较好的结果。

3 实验结果分析

本文算法在visual studio2010环境中，采用C++编码实现，实验微机的CPU主频为2.0 GHz，表3的航班数据为首都国际机场2007年6月13日上午9：40至11：00间的真实数据。算法参数如下：粒子群规模N为30，记忆库中的免疫记忆粒子个数m为8，每一代随机产生的新粒子的个数M为15，最大迭代次数为2 000。

对航班数据经过多次运行计算，分别就先来先服务（FCFS）和免疫粒子群算法（DIPSO）的结果进行对比，获得两种算法的调度方案及总的延误费用，为方便与FCFS作对比，在表3中本文算法的序列值是相对于FCFS的序列经DIPSO算法计算后调整的序列。

调度结果表明，改进的免疫粒子群算法与传统的先来先服务（FCFS）相比较，有效降低了航班的总延误费用。此外为了进一步验证本文的算法，就同一航班调度问题，分别利用粒子群算法（PSO）、FSFC和本文提到的免疫粒子群（DIPSO）运算结果的各项性能指标做了对比，如图4和表4所示。

从图4和表4可以看出，动态免疫粒子群算法（DIPSO）的运算结果明显优于PSO和FCFS算法，DIPSO算法结果的稳定性较好、收敛效率较高，管制员的工作负荷得到有效减小，由此可见，引入免疫机制的DIPSO算法能够较为稳定的获得最优解，更加适用于航班着陆调度问题。

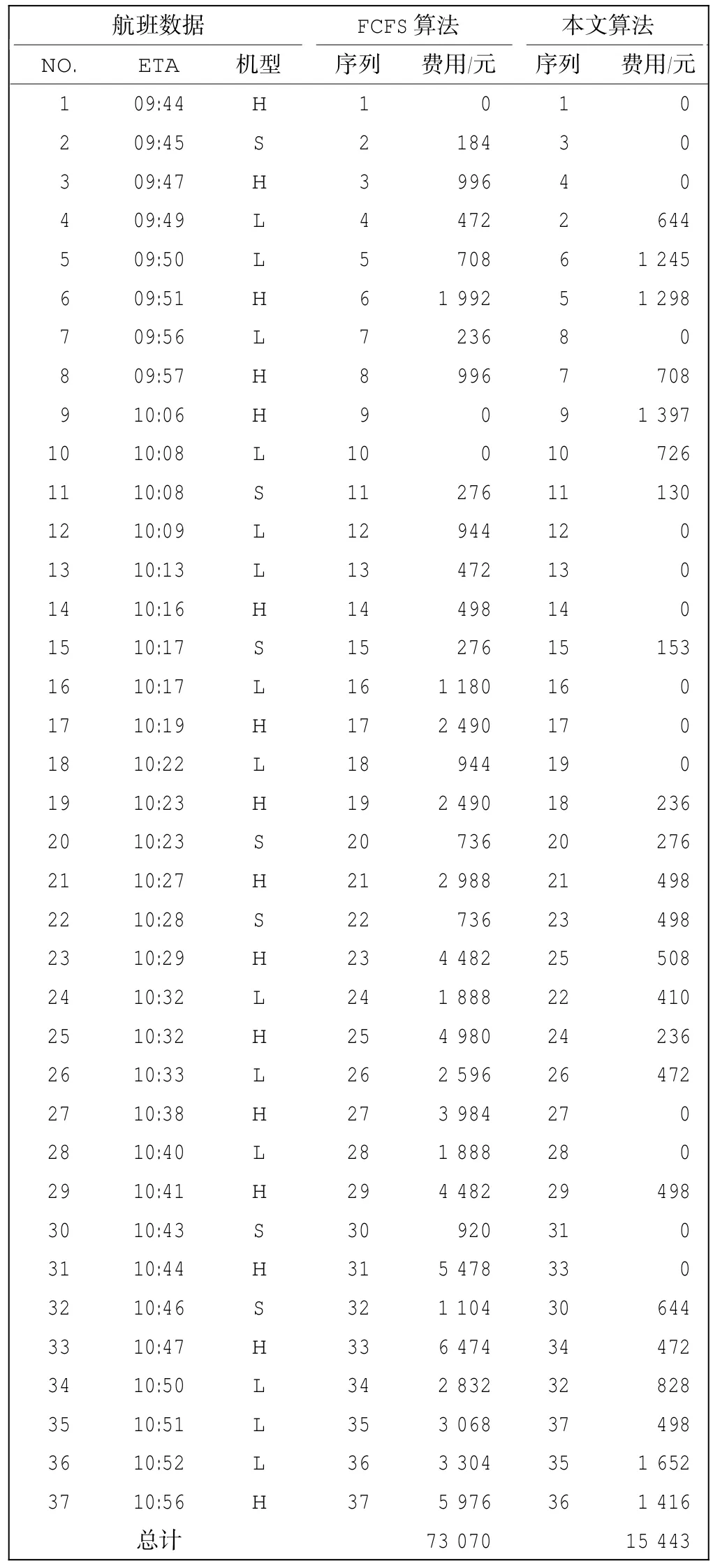
表3 航班数据及调度结果Tab.3 Flight data and scheduling result

图4 迭代收敛对比图Fig.4 Comparison of iteration restrains

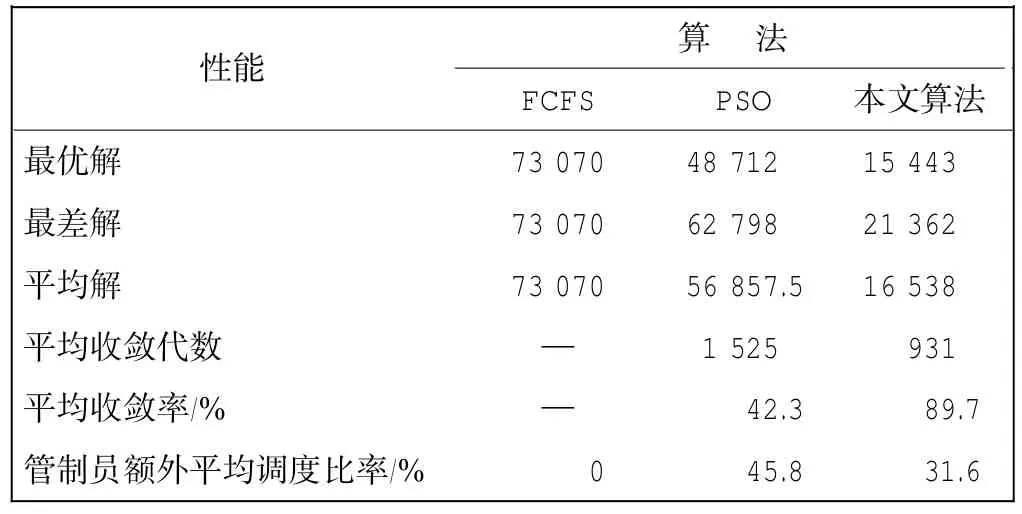
表4 算法性能比较Tab.4 Performance comparison of 3 algorithms

4 结语

本文针对现实航班着陆调度多约束问题，结合滑动时间窗，解决动态航班着陆问题，借鉴生物免疫系统的免疫机制，引入免疫记忆库和粒子浓度选择对传统PSO算法进行改进，同时，以额外耗费成本最小为目标函数，在保证安全且较为公平的原则下有效安排着陆航班的序列。DIPSO在航班着陆调度问题中的进一步研究方向包括：①航班着陆调度问题是一个多约束调度，在实际调度中往往较为复杂，仍需继续探索DIPSO算法在更多现实约束条件下ALS问题中的应用；②大型机场的跑道往往不止一条，需综合考虑航班的起飞与着陆在多跑道中的合理利用。

[1]VOLCKERS U.Arrival Planning and Sequencing with COMPAS-OP at the Frankfurt ATC-Center[C]//Proceedings of the 1900 American Control Conference，California，San Diego，1900：496-501.

[2]JOHN E.Fuzzy Reasoning-Based Sequencing of Arrival Aircraft in the Terminal Area[C]//AIAA Guidance，Navigation and Control Conference，New Orleans，LA，1997：1-11.

[3]BEASLEY J E，KRISHNAMOORTHY M，SHARAIHA Y M，et al.Displacement problem and dynamically scheduling aircraft landings[J]. Journal of the Operational Research Society，2004，55：54-64.

[4]张 伟，王 宏.求解机场终端区航班着陆调度问题的遗传算法[J].计算机工程与应用，2012（12）：931-938.

[5]冯兴杰，孟 欣.基于遗传算法的动态航班着陆调度优化[J].计算机与现代化，2012（1）：181-187.

[6]刘 朕，李 锐.飞机着陆调度优化的混合免疫克隆算法[J].计算机应用与软件，2013，30（2）：116-121.

[7]余 静，杨红雨，马博敏，等.证据理论在机场动态容量预测模型中的研究[J].电子科技大学学报，2010，39（1）：141-144.

[8]刘 洪，杨红雨，彭莉娟.基于分组的MPS进近航班着陆调度算法研究[J].电子科技大学学报，2013，42（4）：1230-1236.

[9]KENNEDY J，EBERHART R.Particle Swarm Optimization[C]//Proceedings of International Conference on Neural Networks.Perth：IEEE，1995：1942-1948.

[10]段 富，苏同芳.免疫粒子群算法的改进及应用[J].计算机应用，2010，30（7）：1183-1188.

[11]阮旻智，李庆民，王红军，等.人工免疫粒子群算法在系统可靠性优化中的应用[J].控制理论与应用，2010，27（9）：1253-1258.

[12]冯 琳，毛志忠，袁 平.一种改进的多目标粒子群优化算法及其应用[J].控制与决策，2012，27（9）：1312-1319.

[13]SHI Y，Eberhart R C.Fuzzy Adaptive Particle Swarm Optimization[C]// Proceedings of the 2001 Congress on Evolutionary Computation.Piscataway，NJ：IEEE Press，2001：101-106.

[14]雷开友.粒子群算法及其应用研究[D].重庆：西南大学，2006.

（责任编辑：党亚茹）

Dynamic aircraft landing scheduling based on improved immune particle swarm optimization

FENG Xing-jie，LIU Dong
（College of Computer Science&Technology，CAUC，Tianjin 300300，China）

In order to improve the air traffic flow management in airport terminal area，the dynamic flight landing sequence is adjusted to achieve the most effective use of the airport and airspace capacity.To reduce the economic loss of flight delays，a novel dynamic immune particle swarm optimization（DIPSO）is designed，focusing on dynamic change of the aircraft landing scheduling，combining with the sliding time window and considering various realistic constraints，ensuring minimum flight delay cost while taking into consideration the work load of controllers and flight landing fairness.Simulation results show that this model effectively reduces the delay cost in dealing with dynamic flight landing compared with first-come，first-served principle.

immune particle swarm optimization；scheduling of flight landing；dynamic；minimum delay cost

V355.2;TP391.9

:A

:1674-5590(2015)02-0018-06

2013-12-24；

:2014-01-15

:国家自然科学基金项目（U1233113）

冯兴杰（1969—），男，河北邢台人，教授，博士，研究方向为数据仓库、数据挖掘与智能信息处理理论与技术.