阵列协方差矩阵与FOCUSS算法的DOA估计方法*

李前言 康春玉

(1.海军大连舰艇学院研究生队 大连 116018)(2.海军大连舰艇学院信息作战系 大连 116018)



阵列协方差矩阵与FOCUSS算法的DOA估计方法*

李前言1康春玉2

(1.海军大连舰艇学院研究生队 大连 116018)(2.海军大连舰艇学院信息作战系 大连 116018)

传统的波达方向(DOA)估计方法往往受到Nyquist采样定理与“瑞利限”的限制,对快拍数、阵元数及信噪比等条件的要求较高,并且不能准确估计信号源的幅度信息。基于目标在空域的稀疏性,针对多维观测向量模型,提出一种正则化的FOCUSS稀疏重构算法,可以有效提高低信噪比条件下的估计性能。阵列接收矩阵快拍数大,含噪声信息多,对高分辨的DOA估计影响较大,而通过对阵列的协方差矩阵求高阶次幂的方法可以有效逼近信号子空间,减小噪声子空间的影响。以阵列接收数据的协方差矩阵作为待分解的数据向量构造稀疏模型,能够使重构信号具有较高的分辨率,对快拍数、阵元数及信噪比等条件的要求更低,对旁瓣抑制效果更好,能够较为准确地估计出信源的幅度信息,且不需要对信源数目进行预估计,体现出明显的优势。

波达方向估计; 正则化FOCUSS算法; 稀疏重构; 协方差矩阵

Class Number TP301.6

1 引言

信号的波达方向(Direction of Arrival,DOA)估计在雷达、通信、声纳等诸多领域都发挥着重要作用,也是阵列信号处理领域研究的重要内容。常规波束形成(CBF)方法与最小方差无失真响应(MVDR)方法利用不同阵元接收信号间的时间延迟实现方位估计,此类方法对快拍数的需求较大,且受到“瑞利限”的限制,分辨率较低。子空间类方法(MUSIC方法、ESPRIT方法)将接收数据分解成信号子空间和噪声子空间,利用二者的正交性构造出“针状”空间谱实现DOA估计,此类方法虽然估计精度与分辨率都较高,但需要预估信源数目,在实际应用中存在一定的不足。

压缩感知理论是一种新兴的信号处理理论,目前已有许多学者在着手研究压缩感知方法在DOA估计中的应用,并且已取得了一定的成果。压缩感知理论的核心问题就是稀疏重构算法的选择与应用问题,目前应用较多的是凸优化类算法与匹配追踪类算法。这些方法的估计思想都有较大差异,但都必须以单快拍的阵列接收数据位待分解的向量构造稀疏模型,再以多块拍平均的方法得到信源的方位信息,而FOCUSS方法能够实现多维观测向量(MMV)模型的稀疏重构[1],具有计算量小、采样数少、收敛速度快的优势,正则化的FOCUSS方法又能够大大改善DOA估计效果[2]。

直接利用阵列接收数据的稀疏分解进行DOA估计极易受到噪声的影响,对阵列接收数据进行奇异值分解(SVD)能够有效减弱噪声的影响,但此方法需要已知信源数目,当信源数过估计或欠估计时,性能显著下降[3]。阵列接收数据的协方差矩阵包含有接收数据的大部分信息,且能够使矩阵的维数显著降低[4],对协方差矩阵求高阶次幂(HOP)的方法可以有效逼近信号子空间,减小噪声子空间,用此矩阵作为待分解的稀疏向量可以有效减少噪声带来的影响,并且避免了对信源数目的估计和对接收矩阵的特征值分解[5]。

2 DOA估计的数学模型

2.1 阵列信号数学模型

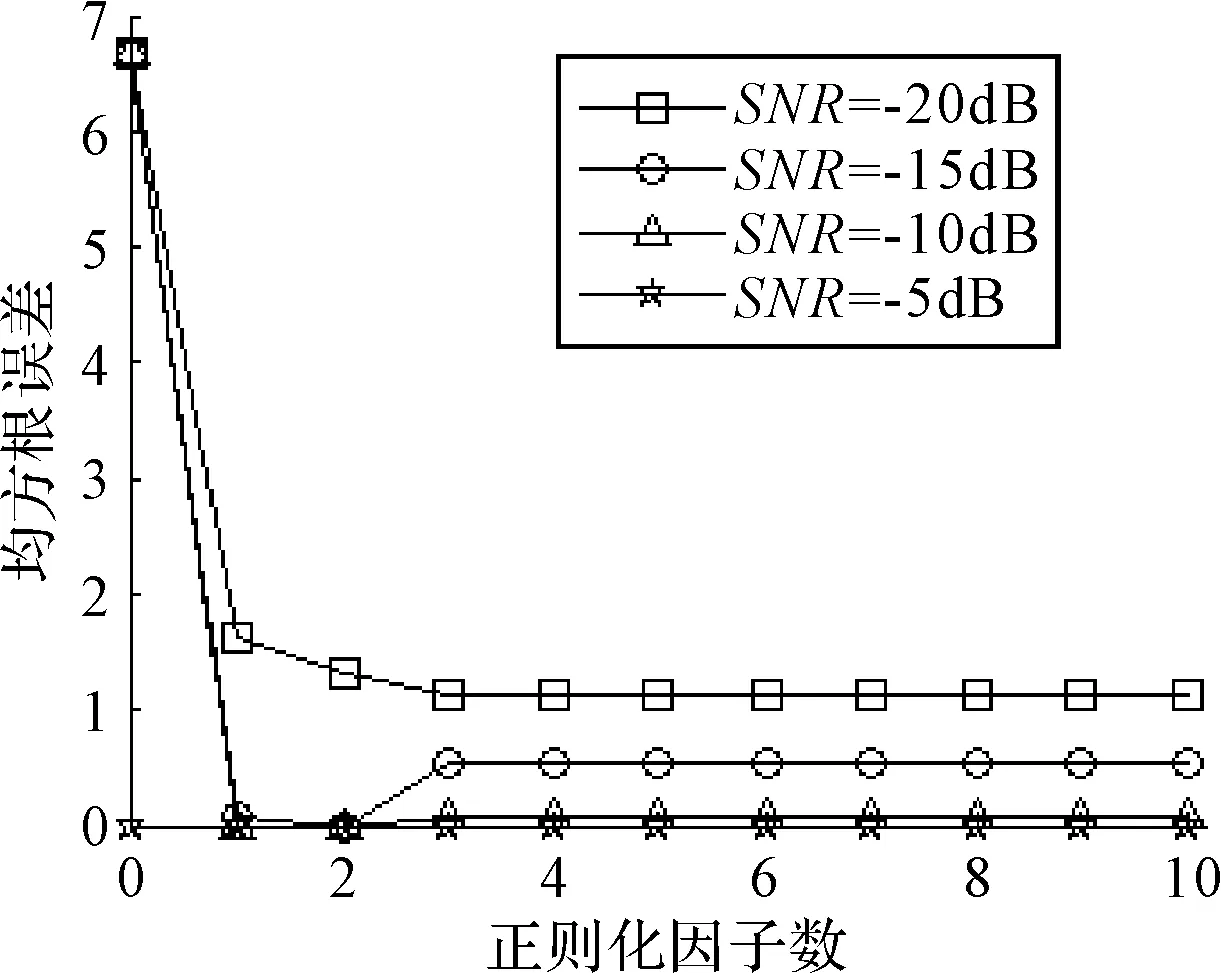
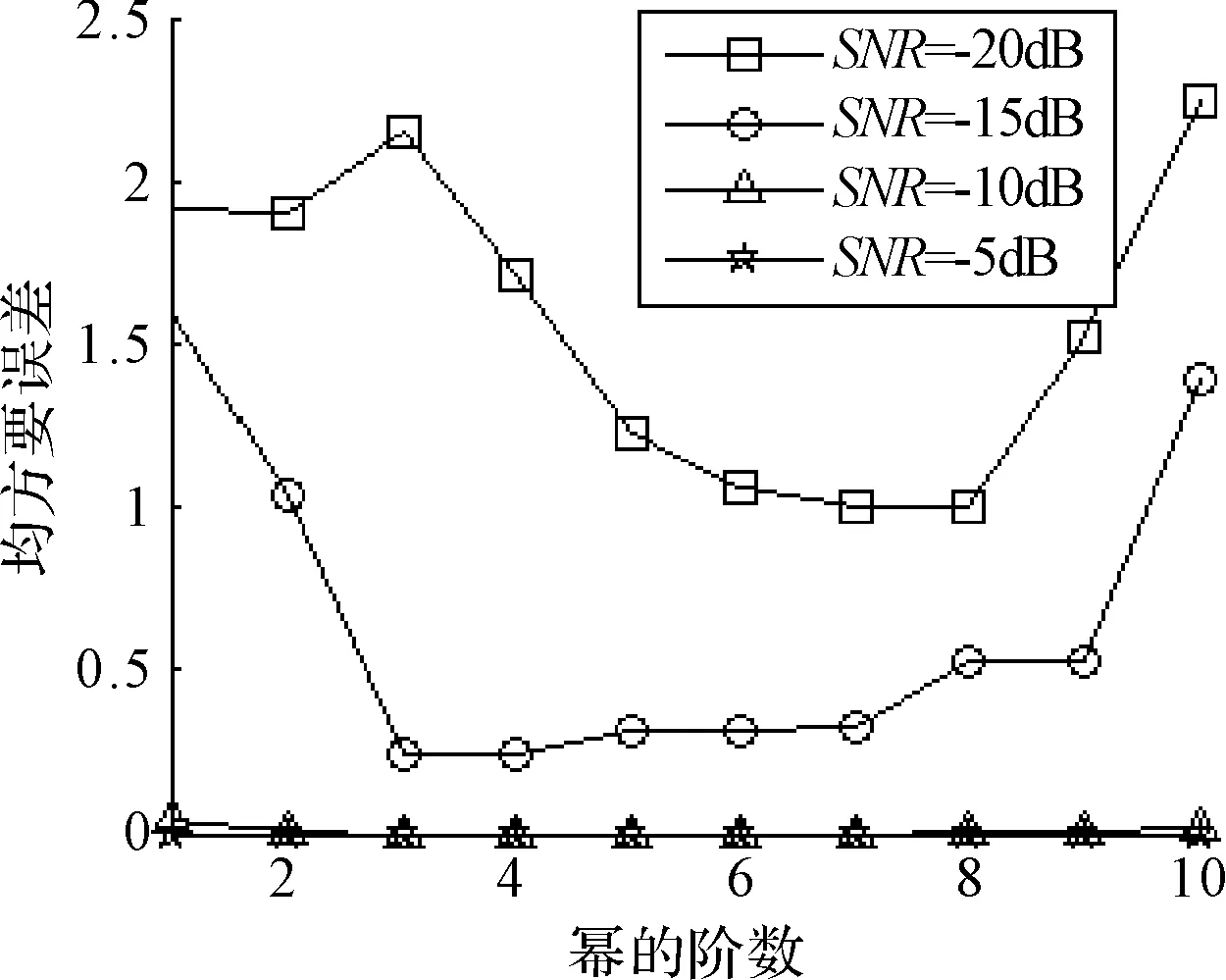
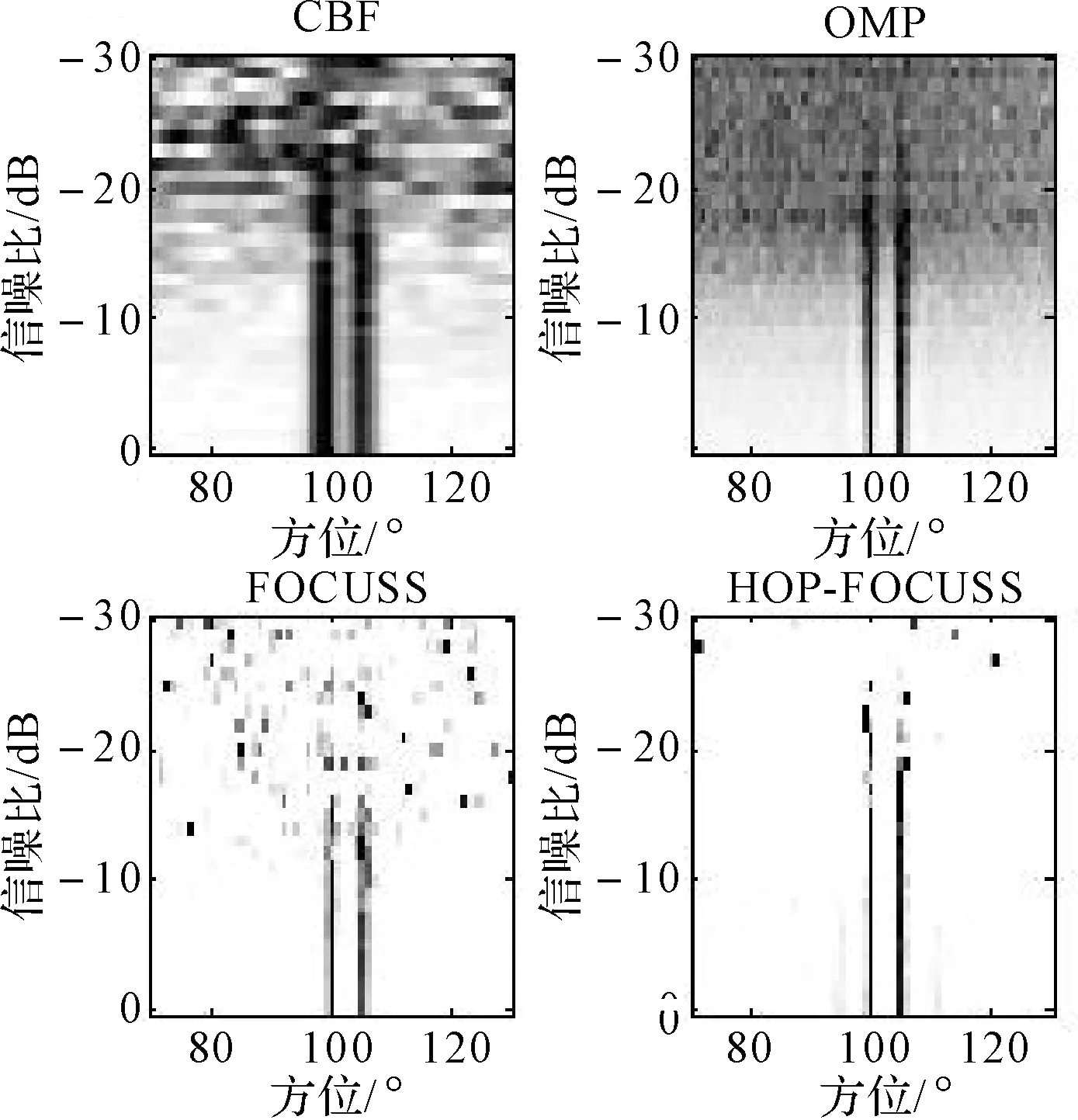
假设均匀线列阵由M个等间距阵元构成,阵元间距为d,空间存在N(N

(1)

式中,ym(t),si(t),nm(t)分别表示t时刻第m阵元的接收信号,第i个目标源信号和第m阵元上的加性噪声,τim表示t时刻第m阵元相对参考点接收到第i个信号的时间延迟,可以表示为

(2)

式中,c为声波在水中的传播速度。

将式(1)写作矢量形式为

Y(t)=A(θ)S(t)+N(t)

(3)

式中,Y(t)为t时刻采集的阵列数据,S(t)为信号源,N(t)为噪声,A(θ)为阵列导向矢量矩阵,可表示为

A(θ)=[a(θ1),a(θ2),…,a(θN)]

(4)

a(θi)=[e-j2πf0τi1,e-j2πf0τi2,…,e-j2πf0τim]T

i=1,2,…,N

(5)

2.2 多维观测矩阵的压缩感知DOA估计模型

假设空间中仅存在少量有限个远场目标源,这样就使得目标源在空间上是稀疏的,满足压缩感知理论的前提条件。

将整个空间均匀划分为{θ1,θ2,…,θH}(H≫N),则根据假设,空间中只在一些位置上存在信号源(N个),在大多数可能的位置并不存在实际的信号源,因此,可以构造稀疏矩阵Aα,表示为

Aα(θ)=[α(θ1),α(θ2),…,α(θH)]

(6)

α(θi)=[e-j2πf0τ1i,e-j2πf0τ2i,…,e-j2πf0τmi]T

i=1,2,…,H

(7)

同时构造出一个空间H×1维信号s,即:

s=[s1,s2,…,sH]T

(8)

s中仅有N个非零元素,其余H-N个元素均为零,且H≫N。对于多维观测矩阵(MMV)的压缩感知模型来说,若阵列接收信号Y有K个快拍,则需要构造出一个与Y维数相同(M×K)维的矩阵x

x=[s(1),s(2),…,s(k)]

(9)

则MMV的压缩感知DOA估计模型为

Y=Aαx

(10)

可以看出,待估计的阵列流形A(θ)是完备阵列流形Aα(θ)的子集,而向量s也是矩阵x的其中一列,即也是x的子集。压缩感知的核心问题就是要解决以下的凸优化问题

(11)

对矩阵x的每一列进行求和平均后便可得到信源的空间谱估计

(12)

通过P(θ)可以实现多快拍的目标方位估计。

3 正则化的FOCUSS重构算法

早在1997年,Gorodnitsky与Rao等研究学者就提出了FOCUSS算法,后经不断改进形成现有的多测量矢量欠定系统聚焦求解(Multi-vectors FOCal Undetermined System Solver,M-FOCUSS)算法。该方法的本质是利用最小2范数来逼近最小0的解,在迭代中加入一个权值W来优化重构函数,首先初始化一个与阵列接收矩阵相同维数的全1阵x,再通过以下迭代求解过程重构原始信号[2]

1)Wk=diag(xk-1)

2)qk=(AαWk)TY

3)xk=Wkqk

(13)

以上的迭代过程是在无噪声环境下推导出的,针对接收矩阵中存在噪声的系统,应用正则化的FOCUSS算法(Regularized-FOCUSS)可以显著减弱噪声影响,使系统更加稳健,正则化的FOCUSS迭代过程为[7]

1)Wk=diag(xk-1[i]1-2/p)

2)Ak=AαWk

3)qk=AkH(AkAkH+γI)-1Y

4)xk=Wkqk

(14)

式中,p∈(0,1]为稀疏因子,γ为正则化因子。

利用正则化的FOCUSS算法可以实现MMV模型的压缩感知DOA估计,并且可以有效抑制噪声,提高估计性能。

4 基于阵列协方差矩阵的DOA估计方法

直接利用阵列接收的快拍数据进行DOA估计容易受到噪声影响,Malioutov等提出了1-SVD方法,对阵列接收矩阵进行奇异值分解(SVD),然后利用最小1范数的约束条件重构原始信号。此方法对抑制噪声有能够起到较好的效果,但需要较为准确地估计出信源数目,在实际应用中存在一定的不足。

而利用接收数据协方差向量的稀疏表示方法来实现DOA估计可以明显提高估计性能。

阵列接收数据的协方差矩阵可以通过K次快拍数据估计得到,表示为

(15)

此时,R为一个M×M的矩阵,若对协方差矩阵进行特征值分解,则R可表示为

(16)

式中,ES、EN分别代表信号子空间和噪声子空间,ΛS、ΛN为其相应特征值,而协方差矩阵的特征值又有如下特点

λ1≥λ2≥…≥λN≫λN+1≥λN+2≥…≥λM

(17)

可以看出,信号子空间对应的特征值大于噪声子空间对应的特征值,只要设法增大协方差矩阵中的大特征值,减小小特征值,就可以有效抑制噪声,提高估计效果。

但通常情况下,协方差矩阵特征值的区分程度并不明显,噪声特征值往往比较发散。对于式(16),若对协方差矩阵求其m次阶幂,可得到

Rm=ESΣSESH+ENΣNENH

(18)

式中,ΣS=diag{λ1m,λ2m,…,λNm},ΣN=diag{λN+1m,λN+2m,…,λMm}。

由于经过高阶幂的运算后,大特征值增加的幅度远远大于小特征值增加的幅度,即λ1m≥…≥λNm≫λN+1m≥…≥λMm,因此高阶幂的协方差矩阵中的小特征值可以忽略不计,表示为

(19)

这就表示阵列协方差矩阵在经过m次阶幂后已经逼近于信号子空间,噪声子空间已经可以忽略不计,这就使得矩阵Rm可以最大程度地逼近于原始信号。而实际应用中,参数m并不需要取到极限,只需要取有限次的整数就完全能够满足收敛要求[8]。

5 实验仿真验证

假设均匀线列阵阵元间隔为0.5m,两个远场窄带相干信号源的方位分别为10°和15°,频率均为1400Hz,采样频率为25kHz,声速为m/s,{θ1,θ2,…,θH}的角度间隔为1°。

5.1 正则化FOCUSS方法中正则化因子的选取

假设均匀线列阵中阵元数为32,快拍数位128,噪声为高斯白噪声。考虑FOCUSS算法中正则化因子γ对估计效果的影响,计算信噪比在-20dB,-15dB,-10dB及-5dB四种情况下,随着γ数值的变化,FOCUSS算法估计出的方位与真实目标方位的均方根误差(RMSE),得到四条曲线如图1所示。

图1 随着γ的变化FOCUSS算法的RMSE曲线

从图1可以看出,采取正则化的FOCUSS方法能够有效减小均方根误差,提高估计准确性,但随着γ数值的进一步增大,均方根误差不会有明显的改善,反而有可能增大,因此再此方针背景下,选择γ在2左右为宜。

为了准确反映空间谱信息,增加快拍数至1024,令γ的值为2,得到CBF方法、MVDR方法、FOCUSS方法及正则化FOCUSS方法的空间谱如图2所示。

图2 四种估计方法的空间谱

从图2可以看出,在有噪声干扰的情况下,未正则化的FOCUSS方法无法准确估计目标的方位,而正则化的FOCUSS方法却明显能够改善估计效果。且相对于CBF方法与MVDR方法,正则化的FOCUSS方法对噪声的抑制效果更好,对方位的估计更加准确。

5.2 协方差矩阵高阶幂方法中幂指数的选取

在与5.1节相同的方针背景下,假设两目标的归一化强度均为1,随着幂指数m的变化,得到HOP-FOCUSS方法在不同信噪比情况下的RMSE曲线如图3所示。

图3 随着m的变化HOP-FOCUSS方法对相同强度目标的方位信息估计的RMSE曲线

从图3可以看出,利用阵列协方差矩阵作为待分解的稀疏向量可以显著提高方位的估计准确率,减小估计误差,尤其在低信噪比条件下有较好的效果,幂指数取到合适的值可以使均方根误差达到最小,但在较高信噪比情况下,协方差矩阵的高阶幂方法对方位信息所起到的作用并不明显。

在实际的空域信号中,目标的强度往往是不同的,且伴随着较多的干扰噪声,若无法准确估计目标的强度,则对区分目标与噪声会造成一定的困难,因此对目标的幅度信息较为精确地估计对方位估计也具有重要的意义。此节讨论HOP-FOCUSS方法估计出目标的幅度信息与真实目标的幅度之间的均方根误差。假设两目标的归一化强度分别为1和0.9,其他仿真条件与5.1节相同,得到HOP-FOCUSS方法在不同信噪比情况下对目标幅度信息估计的RMSE曲线如图4所示。

图4 随着m的变化HOP-FOCUSS方法对不同强度目标的幅度信息估计的RMSE曲线

从图4可以看出,在任何信噪比条件下,对协方差矩阵取高阶幂都能够有效提高对目标的幅度信息的估计效果,但随着幂指数的增大,估计效果趋于稳定,不会再得到明显改善。结合图3与图4,可以看出,在此仿真背景下,取幂指数在5左右可以达到最好的估计效果。

假设两个目标的归一化强度分别为1和0.9,快拍数为1024,m的值为5,其余仿真条件与5.1节相同。在此仿真背景下,得到CBF方法,MVDR方法,压缩感知正交匹配追踪(CS-OMP)方法,正则化FOCUSS方法(Re-FOCUSS),高阶幂正则化FOCUSS(HOP-Re-FOCUSS)方法的空间谱如图5所示。

图5 目标强度不同时五种方法估计的空间谱

从图5中可以看出,CBF方法与MVDR方法的方位估计值与真实值有一定的误差,且旁瓣的幅度值很高,影响估计效果,而CS-OMP方法对旁瓣的抑制效果也较差。而直接使用阵列接收数据进行稀疏分解的方法对方位的估计较为准确且能够有效抑制旁瓣,但无法准确估计目标的幅度值,在遇到较强干扰的情况下,无法有效区分目标信号与干扰信号,对准确的方位估计造成较大影响,因此利用协方差矩阵高阶幂进行的DOA估计具有更好的估计效果。

5.3 不同阵元数条件下的比较

固定信噪比为-3dB,阵元数从2～32变化,快拍数为1024,图6表示阵元数变化时CBF方法、OMP方法、FOCUSS方法、HOP-FOCUSS方法得到的二维方位历程。

图6 阵元数变化时四种方法估计的二维方位历程

从图6可以看出,CBF方法在阵元数为20时才可以分辨两个目标,且波束宽度较宽,OMP方法与FOCUSS方法在阵元数达到16个时就可以分辨两个目标。而HOP-FOCUSS方法在阵元数达到8个时就可以有效分辨两个信号。同时,由于阵列的协方差矩阵是M×M维的矩阵(M为阵元数),因此利用协方差矩阵的高阶幂作为待分解的稀疏向量,可以使运算的快拍数从1024个减少至M个,从而大大降低运算量,加快估计速度,使之更适应于实际应用。

5.4 不同信噪比条件下的比较

固定阵元数为32,信噪比从-30dB～0dB变化,快拍数为1024,图7表示信噪比变化时CBF方法、OMP方法、FOCUSS方法、HOP-FOCUSS方法得到的二维方位历程。

从图7可以看出,CBF方法、OMP方法、FOCUSS方法在信噪比达到-15dB的情况下才能有效分辨两个目标,且对旁瓣的抑制效果较差,在低信噪比时存在较多的虚警。而HOP-FOCUSS方法在-20dB的情况下就能够有效分辨两个目标,且对旁瓣抑制效果更好,两个目标在历程图上的显示更加明显。

图7 信噪比变化时四种方法估计的二维方位历程

6 结语

针对空域目标的稀疏性,着眼于压缩感知理论中的FOCUSS重构算法及以阵列协方差矩阵的特点,通过对两者计算方式的结合并加以改进,得到HOP-FOCUSS方法对空域目标进行有效的DOA估计。实验仿真证明,FOCUSS方法实现了压缩感知中的MMV模型,降低了运算次数,正则化的FOCUSS方法以及对阵列协方差矩阵求高阶次幂的方法能够有效提高对目标的估计性能,HOP-FOCUSS方法在低信噪比、少阵元数条件下依然能够体现出对目标的方位信息及幅度信息较好的估计效果,对旁瓣抑制效果更好,且能够显著减少计算快拍数,降低运算量及运算时间,在目标估计与探测领域具有较好的应用前景。但同时,本文还存有较多问题尚未解决,如在不同仿真背景下的参数选择,在多目标源,多干扰源情况下本文方法的适用性,尤其是当目标信号源强度较小,噪声干扰较大的,阵列协方差矩阵中的大特征值与小特征值区分极不明显的情况下本文方法的适用性还有待于进一步研究论证。

[1] Shane F. Cotter, Bhaskar D. Rao, Kjersti Engan, et al. Sparse solution to linear inverse problem with multiple measurement vectors[J]. IEEE Transactions on Processing,2005,53(7):2477-2488.

[2] 韩学兵.稀疏恢复算法研究及其在DOA估计中的应用[D].北京:清华大学,2011.

[3] 薛会祥,赵拥军.基于CS阵列的DOA估计[J].电子测量与仪器学报,2012,26(3):208-214.

[4] 李新潮,郭艺夺,张永顺.一种未知信源的快速DOA估计算法[J].空间电子技术,2011,1:15-19.

[5] 李鹏飞,钟子发,张旻.未知信源数目的DOA估计方法[J].电子与信息学报,2012,34(3):576-581.

[6] 康春玉,章新华,韩东.盲源分离与高分辨融合的DOA估计与信号恢复方法[J].自动化学报,2010,43(1):129-159.

[7] 薛会祥,赵拥军,陈建宏.基于信号稀疏表示的信源数目和DOA联合估计算法[J].信息工程大学学报,2011,12(6):713-718.

[8] 燕静波.基于压缩感知的DOA估计研究[D].西安:西安电子科技大学,2013.

Direction of Arrival Estimation Method Based on Array Covariance Matrix and FOCUSS Algorithm

LI Qianyan1KANG Chunyu2

(1. Graduate Student Division, Dalian Navy Academy, Dalian 116018) (2. Department of Information Operations, Dalian Navy Academy, Dalian 116018)

Traditional direction of arrival estimation method is always limited with Nyquist sampling theorem and Rayleigh limit, requires better condition such as snapshot number, sensor number and SNR. It also can’t estimate amplifier information of source accurately yet. Based on spatial sparsity of targets, aiming at multiple-dimension vectors model, regularized FOCUSS sparse reconstruction algorithm can improve performance of DOA estimation in the condition of low SNR effectively. Array received matrix has large snapshot number and lots of noise information and it may affect higher resolution DOA estimation deeply. High power of the covariance matrix can approach signal subspace effectively, decrease the influence of noise subspace. Taking the covariance matrix of array received data as data vector to be resolved construct sparse model can improve resolution of reconstructed signal, and requires less snapshot number, less sensor number and lower SNR. This method can also restrain sidelobe better and estimate amplifier information of source accurately. Moreover, it doesn’t need to pre-estimate the number of sources, reflects obvious advantage.

direction of arrival estimation, regularized FOCUSS algorithm, sparse reconstruction, covariance matrix

2015年3月2日,

2015年3月27日

李前言,男,硕士研究生,研究方向:水声信号处理。

TP301.6

10.3969/j.issn.1672-9730.2015.09.016