基于管制员工作负荷的扇区容量评估方法研究*

任 民 闪 乐

(1.海军指挥学院二系 南京 210016)(2.南京航空航天大学民航学院 南京 210016)



基于管制员工作负荷的扇区容量评估方法研究*

任 民1闪 乐2

(1.海军指挥学院二系 南京 210016)(2.南京航空航天大学民航学院 南京 210016)

为准确评估某一空域容量,论文提出一种基于人类动力学测定管制员工作负荷的方法,该方法通过对管制员通信工作负荷特性进行分析,确定管制员工作过程属于典型人类动力学,符合幂律分布。在此基础上,利用多元线性回归基本模型建立了基于管制员工作负荷的扇区容量评估模型。最后通过案例分析验证了扇区容量评估模型的准确性。

空中交通管理; 容量评估; 人类动力学

Class Number V355.1

1 引言

终端空域的空中交通管制服务是由管制员来实施进行的,准确地评估管制员工作负荷是确定空域容量的基础[1]。目前在该领域主要针对以下三个方面进行管制员工作负荷研究:第一是通过对管制员的生理状态指标和行为种类数目的监测。由于难以确定众多生理和行为指标的重要程度、各指标之间的关联性等,导致评估工作较难实现[2]。第二是通过观察和问卷形式的主观测评管制员工作负荷,但该方法存在难以度量主观精神工作负荷的局限性[3]。第三是通过评估不同的空域复杂程度下的管制指挥,获取管制员工作负荷的水平。该方法对不同空域下的交通特征进行研究,进而确定管制员的工作负荷水平[4]。

除上述三种管制工作负荷研究外,理解和掌握空中交通系统中管制行为的动力学规律,可为确定管制员工作负荷准确评估提供依据,也是实现空域容量预测的前提和基础。本文结合现有人类动力学方面的研究成果,将其运用到管制员的工作负荷中,提出基于人类动力学的终端容量评估方法。

2 管制员通信工作负荷的人类动力学分析

幂律分布及各种包含幂律分布的扩展分布形式是人类动力学中普遍存在的分布形式[5]。数学上,随机变量X的概率密度函数如果可用如下公式表示:

f(x)=Cx-α

(1)

则称变量X服从幂律分布。式中α是一个常量,被称为幂律分布的幂指数或标度参数,幂律分布是一类特殊的重尾分布形式,它具有多种多样的表现形式并广泛存在于众多学科领域之中[5]。

经过研究表明[6],线性装箱法需要大量数据支撑且要求的箱体宽度要很精确,而这在实际应用中很难实现(通常应用中设置的箱体宽度比较随机),故其在求解过程中的不是最优的;对数装箱法虽然解决了数据需求方面的问题,但仍然对箱体宽度的选择有较高要求;累积分布函数拟合法对变量的累积分布函数进行分析,避免了选择箱体的问题,但其仍不能直接求得α的值,而是通过求α+1得到α的值,其中难免会形成一定的误差;而极大似然估计法则可避免上述问题,故本文采用极大似然估计法进行求解,具体过程如下。

对常数C做归一化处理,归一化方程为

(2)

若α>1,则上式可简化为

(3)

则幂律分布方程为

(4)

给出由n个xi组成的集合{xi},则分布中xi出现的概率与下数成正比:

(5)

该数称之为数据集的似然值。而真正想得到的是基于集合{xi}的α的概率值,由贝叶斯定律可知:

(6)

数据的先验概率P(x)是固定的——在集合{xi}中为1,其他时候为0。通常认为,在没有任何不满足该条件的情况下,指数α的先验概率P(α)是统一的,即一个常数。因此,P(α|x)∝P(x|α)。为方便起见,通常使用极大似然函数L的对数值logL来代替的P(α|x)对数值,它们在数值上是相等的,其中:

(7)

现在通过α的极大似然估计值来计算最可能的α值。由于L是个单调增的函数,令δL/δα=0,可得:

(8)

或者

(9)

定义1 管制事件为一段连续的包含一条或多条管制指令(包括给机长发布指令和听机长复述指令)的语音通话。

其中,相邻管制事件间的间隔时间X是本文主要研究对象。通过对具体空域的录音数据分析可以得到连续管制事件的间隔时间,并按上述方法求得相应的α值,即可求得对应管制员通信工作负荷的人类动力学函数。

依据幂律函数的性质,由公式:

(10)

求得样本的数学期望E(X),则该扇区一小时内管制事件的发生频率为3600/E(X)。

3 基于人类动力学的终端容量预测

终端空域由若干扇区构成,而每个扇区中管制事件的发生必然与该扇区空域内的航空器数量有关,即当空域内无航空器时,管制事件就不会发生。据此,本文利用多元线性回归分析的方法来建立各扇区的容量评估模型,最后通过综合评定来确定整个终端空域的预测容量值(由于航路的联系各扇区间相互关联,终端空域容量不是简单的将各扇区容量值相加求和得到)。多元线性回归的基本模型为

y=β1X1+β2X2+…+βnXm+e

(11)

通过对原始数据集的分析和整理,共提取如下模型求解变量:某时段管制事件发生的次数、对应时段扇区各走廊口进出港及飞越航空器的数量、对应时段扇区内进出港及飞越航空器的数量。回归模型的响应变量为某时段管制事件发生的次数。经线性回归分析及求解,综合评价了预测变量对模型的贡献作用,本文最终选择了三个预测变量:即对应时段扇区内的进场航空器数量、离场航空器数量和飞越航空器数量。

定义2 因变量y为单位时间内管制事件发生的次数,自变量x1、x2、x3分别为单位时间内空域中的进、离场及飞越航空器的数量。

建立的回归方程如式(2):

y=β1x1+β2x2+β3x3+e

(12)

通过对前文所述扇区的数据的采集与处理,可以获得回归方程中需要的各变量值,利用多元线性回归法可以求得相应的回归方程。根据得到的回归方程,分析扇区内的管制员工作负荷,并参照DORATASK方法[7]评估扇区的容量。由于DORATASK方法设定了80%的阈值标准,则评估时间内的管制事件发生频率变为2880/E(X)。以此作为约束条件,带入已知的回归方程,从而确定对应扇区的空域容量。

4 算例分析

提取由成都终端空域某扇区的录音数据分析得到1000个连续管制事件的间隔时间,通过对这些数据观察可知管制事件具有阵发性,即在某些时段会集中发生,间隔时间短,发生的频率高(如8h～11h、14h～17h、19h～21h),而其余时段则有较长的间歇时间。这样的分布是符合实际的工作情况的,管制事件高发时段恰恰为实际运行单位的繁忙时段。

对已知数据进行分析,采用极大似然估计法并按照公式(9)计算得出幂指数α=2.55,并用已知幂指数为2.55的理论曲线和数据的散点图进行类比。其分布情况及密度分布情况如图1和图2所示。由图2可以明显的观察到管制事件间隔时间的密度分布具有明显的重尾特性,说明其的确符合幂律分布。

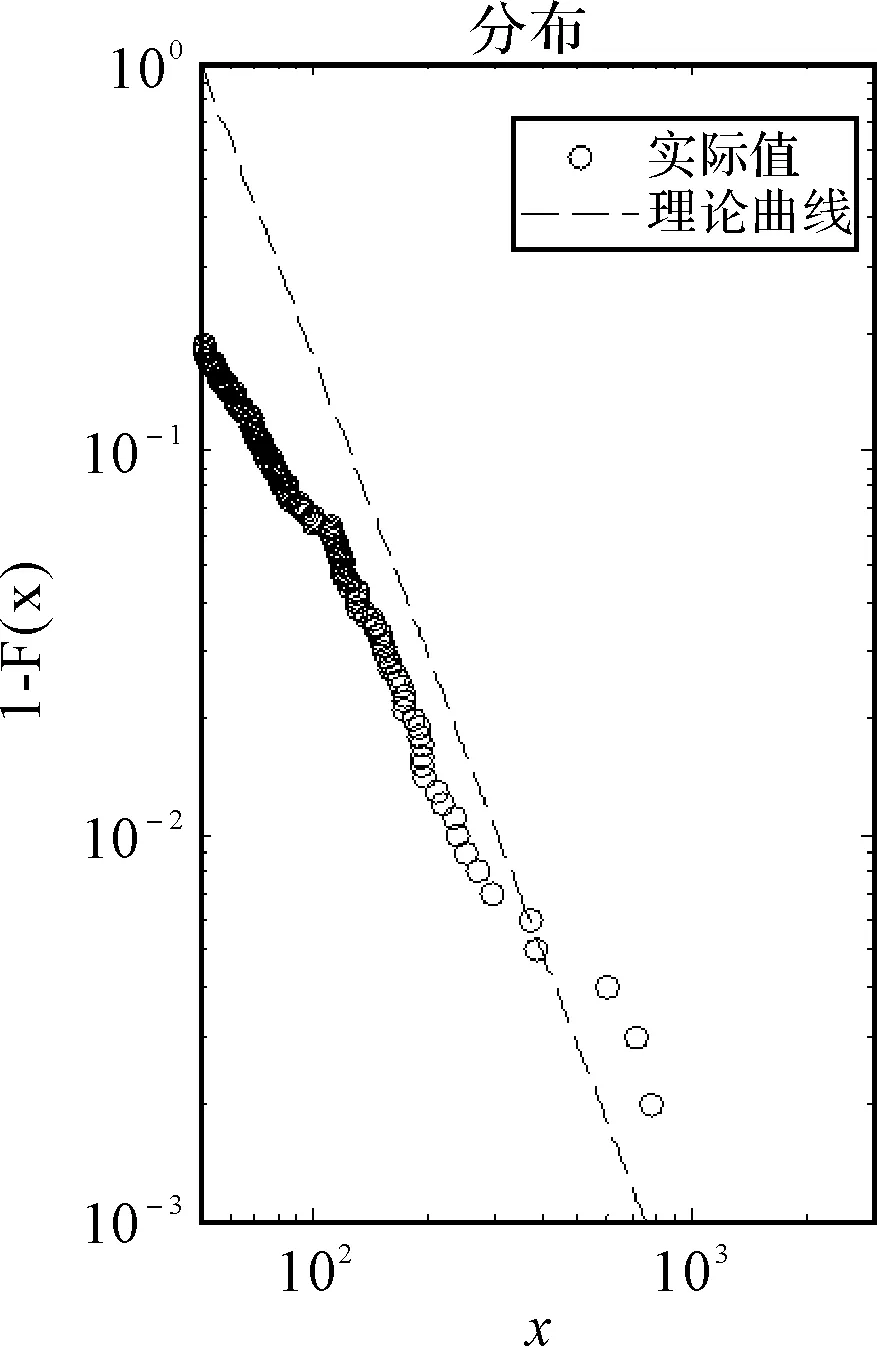
图1 管制事件时间间隔的分布

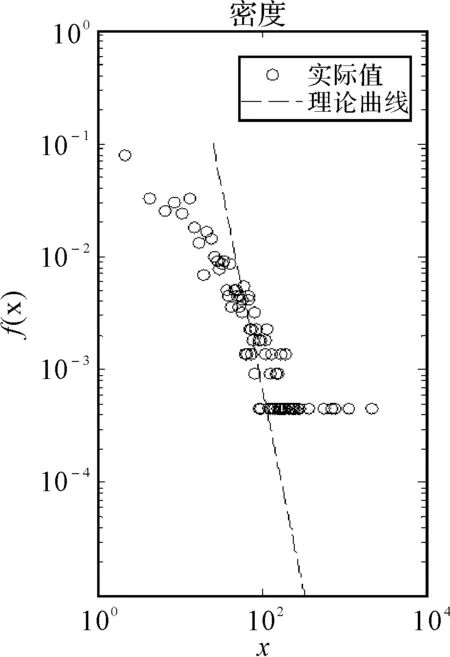
图2 管制事件时间间隔的密度分布

经过进一步的拟合得到该样本下的管制事件的密度函数为

f(x)=122.36x-2.55

(13)

由式(10)计算得E(X)=47.21s,则该扇区一小时内管制事件的发生频率为3600/47.21≈76次/小时。

分析回归方程中需要的各变量值,其中部分样本数据如表1所示(表中数据持续时间段均为1小时)。

对总体样本进行回归分析,根据多元线性回归分析的结果,确定最终的模型为

y=1.385x1+2.768x2+1.75x3

(14)

从回归模型的系数来看,离场航空器对管制事件的发生次数影响最大,其次是飞越航空器对管制事件的影响。考虑到实际管制中区域管制室的指挥席管制员的大部分精力用于指挥从进近扇区移交过来的离场航空器,以及对飞越航空器进行扇区之间的移交,故回归模型中系数的大小关系是合理的。

考虑成都区域雷达管制指挥席管制员的实际工作情况,可以发现管制事件是其工作的重心,与航空器之间的语音通信占据了其工作时间中的绝大部分,这部分工作包括给机长下达相关机动指令和听机长对指令进行复述。除此之外,管制员在实际工作中还涉及很少一部分诸如拖拽标牌等主观负荷,由于受到各管制员的行为习惯影响,所表现的主观性较强,所以没有在回归模型中考虑这些因素。最后,现在实施的是雷达管制,指挥席管制员还需关注雷达显示屏,只要管制区域内有航空器,按照规定管制员必须对其进行监视。由于监视活动很多时候是与管制事件同时发生的,故可认为管制事件中已包含此部分负荷,所以本文的模型中没有考虑监视活动的影响。

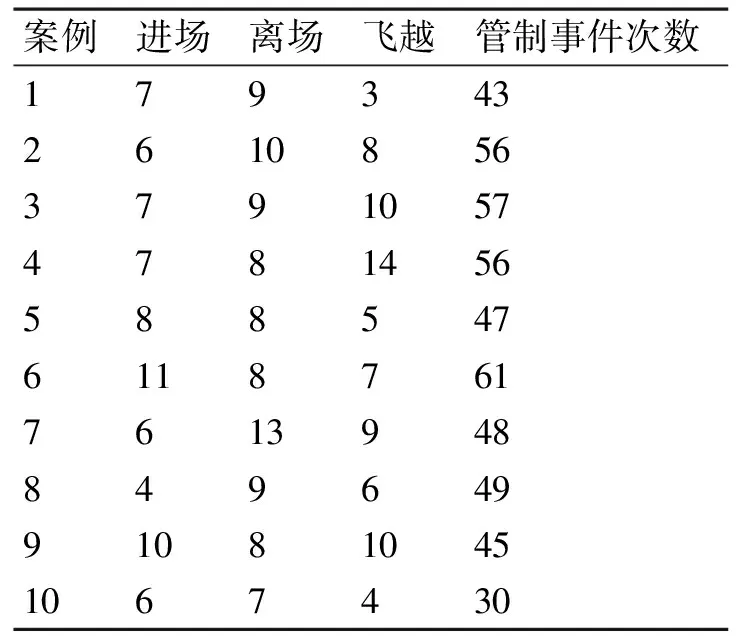
表1 部分管制事件及对应架次数据

根据得到的回归模型(14),可以分析扇区内的管制员工作负荷。由于DORATASK方法设定了80%的阈值标准,则评估时间内的管制事件发生频率变为2880/47.2.1≈61次/小时。

根据实际运行情况,设定进离场比例为1∶1,进离场总架次分别从25架次/小时到37架次/小时,分别计算扇区内飞越的航空器占扇区内总航空器数量的30%、40%、50%时对应的管制事件的发生次数,可得出如下结论:

1) 飞越数量占扇区内所有飞机数量的30%时,运行容量为30架次/小时;

2) 飞越数量占扇区内所有飞机数量的40%时,运行容量为31架次/小时;

3) 飞越数量占扇区内所有飞机数量的50%时,运行容量为32架次/小时。

同样的,用此方法考察终端空域中的各个扇区,即可得到对应扇区的运行容量值,最后综合考虑机场容量和最先达到饱和的扇区等容量限制因素,利用加权求和的方法获得终端空域的运行容量值。

5 结语

本文研究了基于管制员工作负荷的扇区容量评估问题,将人类动力学的相关研究运用到管制员工作负荷评估研究中,并运用回归分析的方法建立了整套的容量评估模型。与以往的研究相比较,本文简化了模型,考虑了飞越航空器对扇区容量的影响,并简化了数据的统计工作,增加了模型的可操作性和普适性。最后,结合成都地区的数据,验证了模型的可行性,评估结果是合理的。

[1] 2012年全国民航运输指标统计公报[R].中国民用航空局,2012.

[2] Doc9426-AN/924. Manual for air traffic service plan[S]. International civil aviation organization,2010.

[3] Zhou T, Kiet H A T, Kim B J, et al. Role of activity in human dynamics[J]. Europhysics Letters,2008,82(2):105-108.

[4] Clauset A, Shalizi C R, Newman M E J. Power-law distributions in empirical data[DB/OL]. [2013-11-10]. http://arxiv.org/abs/0706.1062v2.

[5] Wikipedia. Pareto_distribution[DB/OL]. [2013-11-10]. http://en.wikipedia.org/wiki/Pareto_distribution.

[6] Hong W, Han X P, Zhou T, et al. Heavy-tailed statistics in short-message communication[J]. Chinese Physics Letters,2009,26(2):132-136.

[7] 中国民航局空中交通管理局,IB-TM-2009-008,空域建模与评估实施方法指导材料[S].中国民航局空中交通管理局,2009.

[8] 彭文华,卫平凡,刘国光.基于效能的舰炮武器系统RMS指标设计方法[J].舰船电子工程,2010,30(1):172-174.

[9] 张兆宁,王莉莉.空中交通流量管理理论与方法[M].北京:科学出版社,2009:79.

The Evaluating Method of Sector Capacity Based on the Workload of ATC

REN Ming1SHAN Le2

(1. Second Department, Navy College of Command, Nanjing 210016) (2. Civil Aviation College, Nanjing University of Aeronautics and Astronautics, Nanjing 210016)

In order to accurately evaluate airspace capacity, a method was proposed to measure the workload of atc based on human dynamics, the work process of atc was determined to belong to the typical human dynamics by analyzing the characteristics of atc communication workload, and according with power law distribution. On this basis, the evaluation model of sector capacity was established by using multiple linear regression model based on the workload of atc. In the end, the accuracy of the model was verified by the case analysis.

air traffic management, capacity assessment, human dynamics

2015年4月8日,

2015年5月26日

任民,男,副教授,研究方向:兵种指挥、航空兵管制运行。闪乐,男,硕士研究生,研究方向:新一代空管自动化系统。

V355.1

10.3969/j.issn.1672-9730.2015.10.008