基于人工智能的兵棋推演作战分析研究与设计*
2015-03-14钟剑辉傅调平
钟剑辉 傅调平 邓 超
(1.海军陆战学院研究生队 广州 510431)(2.海军陆战学院模拟训练中心 广州 510431)
基于人工智能的兵棋推演作战分析研究与设计*
钟剑辉1傅调平2邓 超1
(1.海军陆战学院研究生队 广州 510431)(2.海军陆战学院模拟训练中心 广州 510431)
20世纪,随着计算机的出现,使得繁琐、严格的兵棋规则可以在计算机中处理,冯·莱斯威茨父子发明的兵棋迎来了新的春天。论文首先从战斗力度量、战斗结果裁判两方面详细分析了兵棋推演与其它战争分析方法的联系,并总结了兵棋推演应用于战争分析的实践意义。接着以兵棋推演为基础,介绍了相关的对策论、有信息的对抗搜索和局部优化搜索等人工智能技术。最后以一个战术想定为背景,详细阐述了设计兵棋系统时应用人工智能需要解决的数字化、博弈树生成和局面评估等问题。
战争分析; 兵棋推演; 机器博弈; 人工智能
Class Number TP18
1 引言
兵棋是普鲁士军人冯·莱斯威茨父子于19世纪发明的一种作战模拟器材,以棋盘来描述地形、地貌,用棋子来描述作战实体和事件,并引入了作战经验和时间概念,在军事人员的参与下形成基于数学计算的作战模拟系统。兵棋可定义为:以推演回合流程、规则和数据裁决两方或多方对抗行动的作战模拟工具[1]。
由于冯·莱斯威茨父子发明的兵棋规则繁琐且严格,普鲁士军人冯·凡尔第把兵棋变成一种图上作业,使得对阵结果主要依据有经验的军官来判断,而不是详细的兵棋规则。图上作业虽然简单易行,但在对阵结果的评判上因为引入的主观因素较多,使这种作战模拟在客观性方面不如兵棋。
20世纪,计算机的出现使得繁琐、严格的兵棋规则可以在计算机中处理,冯·莱斯威茨父子发明的兵棋迎来了新的春天。本文讨论的兵棋,就是这种具有繁杂推演规则的严格式兵棋,其对阵结果的评判不依赖于某个人的判断。本文首先分析了兵棋推演在诸多战争分析方法中的地位,接着介绍了应用推演方式分析战争的技术基础,最后以一个战术想定为背景,详细阐述了设计兵棋系统时应用人工智能需要解决的数字化、博弈树生成和局面评估等问题。
2 基于兵棋推演的作战分析方法
兵棋推演的本质是“推演”,而推演是基于仿真与实验的战争分析方法之一。兵棋推演的分析方法离不开其它定量分析方法,离开了定量分析,兵棋推演就是无水之源、无木之本。
2.1 基于兵棋推演的分析方法与其它分析方法的联系
人们在探索、发现战争规律的实践过程中,不仅创造了军事理论,同时也总结出了许多战争分析的方法。这些战争分析的方法主要包括基于历史与经验的分析方法、基于解析的分析方法、基于仿真与实验的分析方法以及综合分析方法,如图1所示[2]。
基于兵棋推演的分析方法与其它分析方法有着密切的联系,主要涉及如下几个方面:
1) 兵棋棋子战斗力值的度量。在兵棋推演的战斗结果裁决中,为了方便作战模拟的组织实施,让所有的战斗力值都等价。为了得到等价战斗力值,需要用到基于历史经验的定量分析方法。
2) 兵棋推演中战斗结果的裁判。战斗结果的数据可以利用基于随机仿真实验的统计试验法与基于半经验半理论的兰彻斯特方程结合生成。
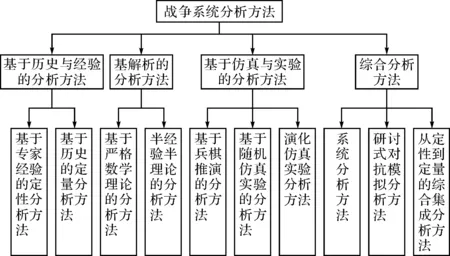
图1 战争系统分析方法
3) 兵棋推演中的决策离不开基于严格数学理论的方法,如对策论。对策论把策略选择的得失表示为定量形式进行研究,为最优策略的选择提供一种算法。

表1 海湾战争兵棋中的各国联队战斗力值(节选)
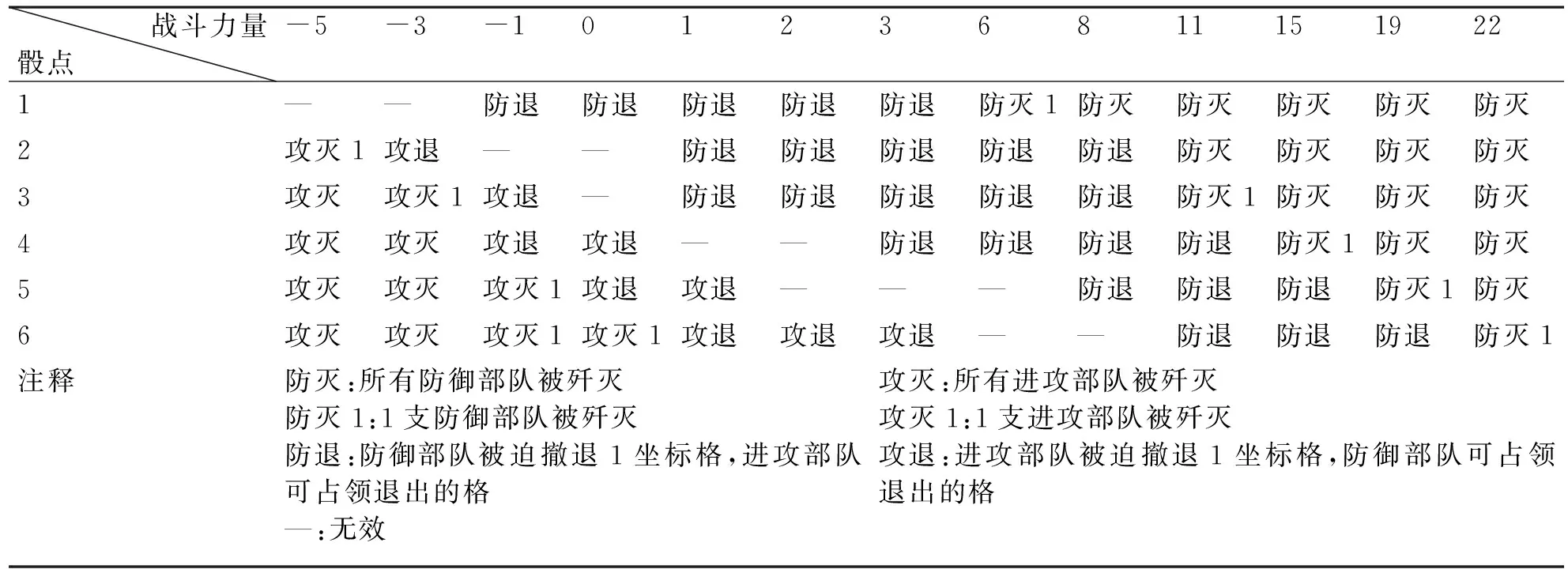
表2 海湾战争兵棋中的地面战斗结果表
2.2 战斗力值的度量
在作战模拟分析中,对部队整体战斗力的度量标准,称为战斗力值。战斗力值的量化过程采取了完全经验式的途径。首先,根据历史经验给武器杀伤力确定量化标准;然后,在此基础上附加各种影响武器杀伤力的量化因素;最后,把得出的这些量化标准放到历史战例中去检验,通过不断修正获得最接近战例实际的战斗力值。
美国军事历史学家杜派在武器的理论杀伤力指数和应用杀伤力指数的基础上,设计出军队战斗力的框架结构,即定量判定模型。这个理论包括两个部分:战斗实力值和战斗潜力值。战斗实力值是经过环境因子修正的应用杀伤力指数总值;战斗潜力值是经过战斗因子修正的战斗实力值。比较敌我双方战斗潜力值的大小,可以对战斗效果的可能性做出推测[3]。
为了方便作战模拟的组织实施,就要使作用于相同目标的战斗力值有一个统一的价值标准,即作用于同一个目标上的各军兵种兵力兵器的战斗力值可以相加,同一场战斗中敌我双方的战斗力值可以相减或相乘。表1中例举了美国1990年出版的模拟海湾战争的兵棋中使用的近千种等价战斗力值的一部分。
2.3 战斗结果的裁判
有了等价战斗力,就能对敌对双方的战斗结果进行基本裁判。兵棋推演存在许多不确定性,需要抽取随机数,导致相同的策略下可能产生很多不同的战斗结果[4]。在战果的裁判中,还需要引入偶然因素。表2为海湾战争兵棋中的地面战斗结果表。表中的结果既可以来自战争经验中的战例统计,也可以利用统计试验法与兰彻斯特方程结合生成。
这种基于战例统计、统计试验的方法,在兵棋中有着非常广泛的应用,伤亡、轰炸、侦察、射击、电子对抗、气象、投降等由偶然因素导致的事件,都设计有专门的概率表,用以确定某一事件是否会发生及其对战局会造成什么样的影响。
2.4 基于兵棋推演的战争分析方法应用于战争分析实践的意义
与其它分析方法相比较,基于兵棋推演的战争分析方法在战争分析实践的应用,具有特殊的意义。
1) 使军事人员在对战争的动态性研究中牢固树立定量分析的思想。随着运筹学在第二次世界大战后的快速发展,解析分析方法得到了广泛的运用。但这种以解析计算为手段的研究方法,即使引入随机变量来考虑随机性因素,一旦初始条件确定,其作战的结果基本上也是确定的,难以反映战争过程中各个体系之间的动态对抗、不断演化的特性。而基于兵棋推演的战争分析方法,既能反映战争的动态、演化特性,同时基于等价战斗力的战果裁决方法的广泛应用,又使动态的作战推演也能实现定量分析。
2) 数字化的兵棋使人工智能技术能够应用于战争的动态分析中。人工智能、机器博弈技术的相关理论及其应用取得了很大的成功,尤其在下棋方面的智能,甚至已经超过了人类。在战争的静态研究中,计算机技术的应用已经取得了很大的成功;而兵棋推演在战争分析中得到积极的应用,是在战争的动态研究中应用计算机技术的基础。
3 兵棋推演中应用人工智能的理论基础
3.1 对策论
对策论又称博弈论,是研究具有对抗或竞争性质现象的数学理论和方法。在这类对策现象中,参加竞争或对抗的各方具有不同的利益和目标。为了达到各自的利益和目标,各方必须考虑对手的各种可能的行动方案,并力图选择对自己最有利或最合理的方案[5]。
为对对策现象进行数学上的分析,需要建立对策问题的数学模型,称为对策模型。对策模型包括三个基本要素:局中人、策略和赢得函数。
“局中人”确定了有权决定自己行动方案的对策参加者,对策论中对局中人的一个重要假设是:每个局中人都是理智的。“策略”是对策中可供局中人选择的一个实际可行的完整的行动方案。一个对策中,每一个局中人所出策略形成的策略组称为一个局势。设si是第i个局中人的一个策略,则n个局中人的策略形成的策略组:
S=(s1,s2,…,sn)
S就是一个局势。当一个局势S出现后,应该为每一局中人i规定一个赢得值Hi(S)。Hi(S)称为局中i的“赢得函数”。

图2 一棵两层的双人博弈树
在对策现象中,由初始状态、后继函数、终止测试和赢得函数等要素定义了一个博弈树。如图2所示是一棵两层的双人博弈树[7]。节点A的值由红方选择,节点B、C、D的值由蓝方选择,终止节点显示了红方的赢得值,值越高被认为对红方越有利,而对蓝方则越不利。所以,节点B、C、D的值由蓝方选择所属叶子节点的最小值3、2、2;节点A的值由红方选择最大值3。在对策中,红方的任务是利用博弈树来确定最佳策略,特别是终止状态的赢得值。
3.2 有信息的对抗搜索
根据对策论,问题的求解过程转变为在博弈树中搜索解的过程,通过遍历博弈树,找出符合条件的一个终止节点。这种搜索策略被称为无信息搜索,按照扩展节点的次序,可分为深度优先搜索、宽度优先搜索、一致耗费搜索[6]。
现实中常常遇到这样的对策现象,由于其博弈树的节点数太多,很少有计算机的主存大小能够满足遍历博弈树所需的存储,而且时间上也不允许。一个典型的例子是国际象棋,其平均分支因子大约是35,一盘棋每个游戏者一般走50步,所以博弈树大约有35100或者10154个节点。这意味着现有计算能力无法找出这类问题的最优决策,无信息搜索策略在这类问题上是无效的。
为此,需要应用有信息的搜索策略来处理这类问题。通过截断函数将非终止节点有效地转变为叶子终止节点,然后由评价函数对要扩展的节点进行选择,使得在最优决策不可处理的情况下,也能做出和取胜的实际机会密切相关的决策。
搜索的性能表现取决于评价函数的质量,质量好的设计应具备如下特征: 1) 评价函数应该以赢得函数同样的方式对终止状态进行排序; 2) 评价函数的计算不能花费太多的时间; 3) 评价函数对于非终止状态的估值应该和取胜的实际机会密切相关。
评价函数的关键元素是基于问题给予的额外信息而设计的启发函数。启发函数的实现有很多方式,其中一种是计算每个特征单独的数值贡献,然后把它们结合起来找到一个总值。数学上称这种函数为加权线性函数
E(s)=w1f1(s)+w2f2(s)+…+wnfn(s)
其中,每个wi是一个权值,fi是棋局的某个特征。
启发函数的应用,一个成功例子是中国象棋对弈程序。根据著名象棋理论家黄少龙提出的理论,可依照千分制的计算方式,制作子力分值表,用于局面评估。比如,帅:无限大;车:1000分;马:开局时400分,中局时450分,残局时500分等等。除了子力分值之外,还有棋子的灵活性、棋盘控制、棋子关系等因素需要考虑[8]。加入这些因素能提高评价函数的知识水平,详细的论述可参考文献[7]。
3.3 局部搜索算法
根据对抗搜索理论,搜索的关键是评价函数的设计,其中启发函数是所求特征的线性或非线性的加权组合,因此,特征权值的确定是评价函数设计的重点。
假设启发函数有n个特征,则其权值数组为[w1,w2,…,wn]。数组的一个取值称为一个具有n个分量的状态,当其中一个状态分量发生变化,则由一个状态转变为另一个状态,且这两个状态称为相邻状态。数组的所有取值组成了状态空间。
上述特征数组的一个状态对应对抗搜索中的一种启发函数。我们需要找到一种方法来寻找状态空间中的最优状态,称为最优化问题。一种方法是人工调整,根据经验,能够确定一些状态分量值的大小及比例。设置这些状态分量,并通过与机器反复对弈,测试获胜机率;然后根据其它经验改变状态分量,试验程序的能力是增强还是降低了;经过多次测试找出一个较优的状态。另一种方法是通过计算机程序辅助,在状态空间中搜索最佳状态。
在对抗搜索中,当找到目标时,到达目标的路径同时也构成了这个问题的一个解。然而在启发函数的特征权值的优化问题中,到达目标的路径与最终路径是无关的。解决这类优化问题的算法称为局部搜索算法,算法从一个当前状态出发,通过某种方式在状态空间中选择最佳相邻状态作为当前状态,直至找到符合目标函数的最佳状态。
局部搜索根据选择相邻状态的方式的不同,可分为爬山法搜索、模拟退火法搜索、局部剪枝搜索和遗传算法搜索。
爬山法搜索又称贪婪局部搜索,它只选择相邻状态中最好的一个,其成功与否在很大程度上取决于状态空间地形图的形状,局部最大值、局部平坦值会影响到最优状态的搜索。为了解决这个问题,已经发展了几种随机算法,用于跳出局部最大和平坦值。
模拟退火搜索是允许下山的爬山法搜索,它随机选择一个状态作为相邻状态。如果该状态优于当前状态,则接受该状态为当前状态;否则,以某个小于1的概率接受该状态为当前状态。这个概率以状态评价指数和倒计时间T为参数,随机相邻状态恶化程度越大,被选上的概率越小;T越接近0,被选上的概率越大。
局部剪枝搜索以k个随机生成的状态开始。然后生成全部k个状态的所有后继状态,形成后继列表。接着从后继列表中选择k个最佳的后继,直至后继列表中存在目标状态。如果一个状态生成了几个好的状态都在k个最佳的后继中,状态群很快聚集到状态空间中的一小块区域内。因此,局部剪枝搜索的缺陷是会使状态缺乏多样性。解决这个问题的方法是按一定概率随机地选择k个后继状态,这个概率是状态评价值的递增函数。
对于一些非线性、多模型、多目标的函数优化问题,用其他优化方法较难求解,遗传算法却可以方便地得到较好的结果[9]。遗传算法搜索是随机剪枝搜索的一个变化形式,它不是通过状态的相邻关系来生成后继的,而是通过随机配对两个父状态结合生成后继,称为杂交。生成的后继状态数组是以随机位置为杂交点,前后两部分分别属于两个父状态数组的一个新数组。状态的评价值与其它状态结合的概率成正比。搜索过程的早期,状态是多样化的,到了后期,随着状态相似度的提高,结合生成的后继状态的变化减少,这点类似于模拟退火。
4 兵棋仿真系统的设计
兵棋仿真系统的设计需要解决如下几个问题: 1) 兵棋各要素的数字化,包括棋盘、棋子及规则的数字化; 2) 博弈树的生成,包括主要是由规则库构成的后继函数、战果判断函数; 3) 局面的评估,包括局面特征的选择、特征加权值的优化。
4.1 想定描述
为了问题描述的方便,参考文献[10]中的一个作战想定来描述系统的设计。
4.1.1 背景
C国和P国之间长期以来一直存在H岛的争议,由于历史原因,几十年来,H岛一直由P国实际控制。C国派遣巡逻艇等在H岛附近海域进行常态化巡逻,保护本国渔船并宣示主权。
作为对C国巡逻的反制,P国也计划派遣舰艇前往相关海域,并企图登岛。为了本国的海洋权益,C国也紧急抽调一支增援编队赶往事发海域,与前线舰只共同守卫海岛主权[10]。
4.1.2 双方兵力对比
C国(以下称红方)的兵力组成包括:三艘巡逻艇(X),五艘快艇(K),一艘轻型护卫舰(F),以及一支包括二艘巡逻艇和一艘快艇的增援编队。
P国(以下称蓝方)的兵力组成包括:三支小型编队以及一艘登陆舰。
4.1.3 双方作战使命
蓝方计划分两个梯次,第一梯次派出两支编队分别从南北两个方向向H岛挺进,其中一个路线是主攻方向,另一个则为助攻方向。作战任务是击退前来拦截的红方舰艇,为后续登陆提供保障。第二梯次,登陆舰在小型编队护送下,突破红方防御,实现登陆的作战目标。
红方为了阻止蓝方逼近H岛,在外围海域构建了一道防线,对蓝方的两条进攻路线进行拦截,如果防御不利,紧急增援编队来不及休整就必须加入作战。双方的初始态势如图3所示。

图3 初始态势图
4.2 兵棋要素的数字表示
4.2.1 棋盘表示
采用正六边形网格来量化地形,如图4所示。

图4 棋盘表示
设原点坐标为(0,0),则绿格坐标为(3,4)。因此棋盘可用一个二维数组来表示:

数组中数值0表示白色格,数值1表示绿色格。
这种坐标系与直角坐标系不同,格与格之间的位置关系不能用二维数组中相邻元素来表示。坐标为(x,y)的格,其相邻格集合Φ为
Φ= {(x-1,y),(x+1,y),(x,y-1),
(x,y+1),(x-1,y-1)}
如图5所示。
图中的橙格与绿格相邻,蓝格距离绿格两步。用数值2、3分别表示橙格与蓝格,这样二维数组为


图5 格与格之间的关系
4.2.2 棋子表示
棋盘二维数组的数据类型为三个数据的结构体,第一个用于标该位置是否有兵力以及兵力是红方还是蓝方;第二个用于标识地形类型;第三个是一个数组地址,该数组中存储有处于该位置的兵力信息,遍历数组能计算出兵力叠加后的攻、防值。
本例中兵力组成不多,分别用数字1~5来表示C国巡逻艇、快艇、轻型护卫舰以及P国小型编队、登陆舰。
4.2.3 战斗力表示
根据3.3节的战斗力值的度量,参考成熟兵棋的等价战斗力量,考虑本想定的兵力情况,战斗力值只涉及舰对舰进攻战斗力值,舰对舰防御战斗力值。具体值如表3所示。
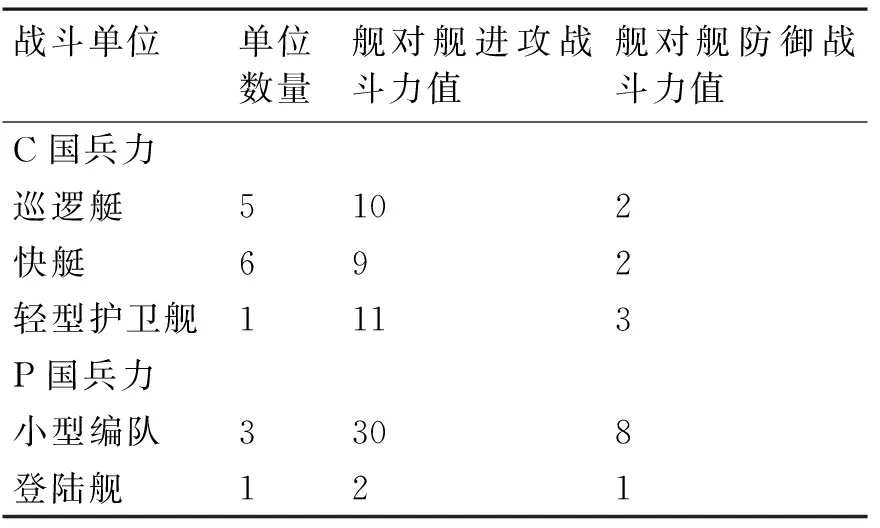
表3 战斗力值
4.3 走法产生器
4.3.1 一般规则
经过简化,棋子的走法遵循如下规则:
1) 红、蓝双方以回合制的方式轮流走子;
2) 每个回合可以对所有棋子进行操作;
3) 每一回合每一个棋子只能走一格;
4) 兵力的移动受到地形的限制;
5) 登岛需要两个回合的时间;
6) 同一方的棋子可以处于一格内。
与交战相关的规则简化如下:
1) 进入已有敌方兵力存在的格子即为交战;
2) 棋子的探测距离为一格;
3) 同一格内的同方棋子攻、防值可叠加;
4) 相邻格的同方棋子的攻、防值叠加可忽略不计。
4.3.2 战术规则
根据战术目的,确定胜负规则如下:
1) 蓝方登陆舰进入H岛相邻格且未被红方攻击,则蓝方能顺利登岛,蓝方胜;
2) 蓝方登陆舰生命值为0,则蓝方败;
3) 40回合内,蓝方未能登岛,则判蓝方输。
其他兵力战术运用规则:
红方后备兵力在双方交战前只能在H岛相邻格活动,双方交战后根据战果选择支援方向;
4.3.3 走法产生器的设计
走法产生器包括下面几个重要的函数:
1) 根据上述规则,设计走法合法性判断函数;
2) 设计走法生成函数,函数有三个形参,包括当前棋盘状态、当前走法的层次、哪一方棋子的走法。该函数遍历棋盘状态下操作方的所有棋子,并通过合法性判断函数筛选出合法走法存入当前层次的数组。
4.4 局面估值函数
以兵棋要素的数据表示及走法产生器的设计为基础,我们能够生成博弈树。根据第3节中介绍的对抗搜索理论,局面估值函数是博弈树中选择扩展节点的关键,这也是人工智能在兵棋推演中运用的核心。我们设计局面估值函数时,可选择“棋子基本价值”、“棋子位置附加值”、“棋子间关系”作为局面的特征。
棋子的基本价值能够反映一个态势的最基本的情况,是估值的过程所不能缺少的。

图6 棋子位置附加值示意图
处于不同位置的兵力,其对达成作战目标的贡献的大小是不同的。根据本案例的战术目的,棋子越靠近H岛,其附加值越高。
我们设定蓝方的棋子位置附加值如图6所示,以H岛为中心,由里向外,第1~10圈的附加值数列为(110,90,70,70,50,50,50,30,30,30)。
附加值矩阵如下所示:

红方棋子的位置附加值与蓝方类似,其附加值矩阵如下所示:

棋子间的关系包括:棋子灵活性、被威胁的信息、被保护的信息、棋子间的配合等。在本想定中,蓝方兵力靠近H岛其价值会增加,但如果红方兵力在旁边,则价值会大打折扣。蓝方登陆舰是其实现战术目的的关键,如果作战编队的护航,其价值也会降低。
特征选择及其权值的确定应充分考虑战法、战术及兵力使用的细节问题。这也正是兵棋推演的价值所在。
5 结语
手工兵棋在作战裁决方面,棋子战斗力以攻防值描述,基本采用力量对比方式,通过表格进行裁决和修正,并考虑偶然性因素,最终得到裁决的结果。其优点是裁决规则简单,可以用于各类部队,不需要对每个棋子都重新建模;缺点也很明显,一般只适于规模较小的行动,不太适合高速平台及精确武器的作战行动,难以完成复杂的联合作战行动的模拟。
古老的兵棋推演方法再次引起人们的兴趣,与其适于应用于计算机技术是分不开的。传统的兵棋需要采用更多的信息化技术,可以在新的信息化系统中加以体现,最终发展成为计算机模拟系统。而采用计算机化的模拟系统,模型规则亟待设计完整,这正是计算机兵棋系统所要研究和解决的问题
[1] 何昌其.战术兵棋发展应用研究[M].北京:解放军出版社,2012:14.
[2] 胡晓峰,等.战争复杂系统仿真分析与实验[M].北京:国防大学出版社,2008:100-176.
[3] 杨南征.虚拟演兵——兵棋、作战模拟与仿真[M].北京:解放军出版社,2007:163-176.
[4] 李乃金.兵棋推演人机博弈决策模型的设计与实现[D].沈阳:东北大学,2009:4.
[5] 胡运权.运筹学教程[M].第三版.北京:清华大学出版社,2007:371.
[6] 胡桐清.人工智能军事应用教程[M].北京:军事科学出版社,1999:9-17.
[7] 姜哲,等译.人工智能——一种现代方法[M].第二版.北京:人民邮电出版社,2010:127.
[8] 王小春.PC游戏编程(人机博弈)[M].重庆:重庆大学出版社,2002:26-27.
[9] 傅调平,陈建华,李刚强.海战智能辅助决策技术及应用[M].军事科学出版社,2010.
[10] 鲁大剑.面向作战推演的博弈与决策模型及应用研究[D].南京:南京理工大学,2013:47-49.
Research and Design of Wargaming Combat Analysis Based on AI
ZHONG Jianhui1FU Tiaoping2DENG Chao1
(1. Graduate Student, Naval Marine Academy, Guangzhou 510430) (2. The Simulation Center, Naval Marine Academy, Guangzhou 510431)
In the 20th Century, with the appearance of computer, the complicated and strict wargame can be processed in computer, thus the wargame invented by Feng rice witts Father receives a new spring. From the aspects of combat strength, and combat result judgement, the relationship between wargame deduction and other combat analysis method is analyzed in detail, and the practical significance of wargame deduction in combat analysis is summarized. Then based on the wargame deduction, the related countermeasure theory, information search and local search optimization are introduced. Finally, in a tactical scenario, the application of artificial intelligence in solving the digital is analyzed.
combat analysis, wargame, game machine, AI
2014年7月8日,
2014年8月27日
钟剑辉,男,硕士研究生,研究方向:战术建模与仿真、人工智能。傅调平,男,博士,教授,硕士生导师,研究方向:战术理论、人工智能、战术建模与仿真。邓超,男,硕士,研究方向:战术建模与仿真。
TP18
10.3969/j.issn1672-9730.2015.01.007
