双频组合观测值解算北斗模糊度的探讨*

陈海岳 汪 捷 徐冠楠

(1.海军湛江航保修理厂 湛江 524002)(2.海军工程大学导航工程系 武汉 430033)



双频组合观测值解算北斗模糊度的探讨*

陈海岳1汪 捷2徐冠楠2

(1.海军湛江航保修理厂 湛江 524002)(2.海军工程大学导航工程系 武汉 430033)

针对北斗双频组合方式,基于矩阵变化和迭代过程,以两种不同线性组合的扩波方法,采用一种新的迭代过程,在满足波长较长以及降低模糊度解相关性的条件下,减小了模糊度搜索空间大小,提高了模糊度解算效率和速度。

北斗双频; 线性组合; 模糊度; 模糊度空间

Class Number V474

1 引言

根据官方公布的数据,北斗导航系统第二阶段和第三阶段都将播发B1,B2和B3三个频率的信号。北斗相应的频率fB1,fB2,fB3分别为1561.10MHz,1207.14MHz和1268.52MHz,对应波长λB1,λB2,λB3分别为19.22cm,24.85cm和23.65cm。正是由于各频率之间存在着相应的比例关系,因此可以将频率之间做线性组合,传统的组合方式包括北斗宽巷组合、北斗窄巷组合、北斗超宽巷组合等,三种方式的优缺点明显,实际应用中根据不同需要选择。本文根据北斗B1,B2和B3中的任意两个频点,在构建观测矩阵方程时,独立考虑双差载波相位观测值和双差伪距观测值,而并非将两种观测值放进同一个方程,最后,在检测判断其可行性时,综合考虑了波长,观测噪声,组合模糊度的方差等因素,还最大程度降低了每一个单一模糊度的相关性,保证定位精度。

为了表达方便,设双差观测方程统一换算成米作单位。

2 传统的直接双频解算法

(1)

将上式中的双差关系上下标省略,简写为

(2)

传统的双频组合方式,例如宽巷组合在求解整周模糊度时,组合波长变长,可以在精度不高的要求下进行解算,窄巷组合之后的观测误差均方差降低,但组合波长变短,因此不利于求解整周模糊度。

根据式(2),分别对进行双频解算的两个频率列出双差载波相位观测方程以及双差伪距观测方程:

(3)

观测方程为L-ε=Ax,根据观测方程列出系数矩阵,即

(4)

(5)

又由于标准差与各自频率之间的关系为

(6)

(7)

在式(4)中,未知向量的标准差可以根据传播矩阵公式计算得到,其值为

(8)

3 改进的北斗双频算法

(9)

(10)

(11)

同样的,设组合后的双频观测方程为

Ld-εd=Adxd

(12)

记T为变换矩阵,xd为待求量。

(13)

则观测向量Ld其协方差矩阵∑Ld可以表示如下

∑Ld=T∑LTT

(14)

同样的,根据误差传播定律可以得到误差协方差矩阵QLd为

(15)

4 改进的算法分析求解

(16)

鉴于北斗双频组合方式很多,通过上述方法可以排除一些不理想的组合,下表给出了几组满足条件的双频组合,组合系数以及组合波长均已给出。

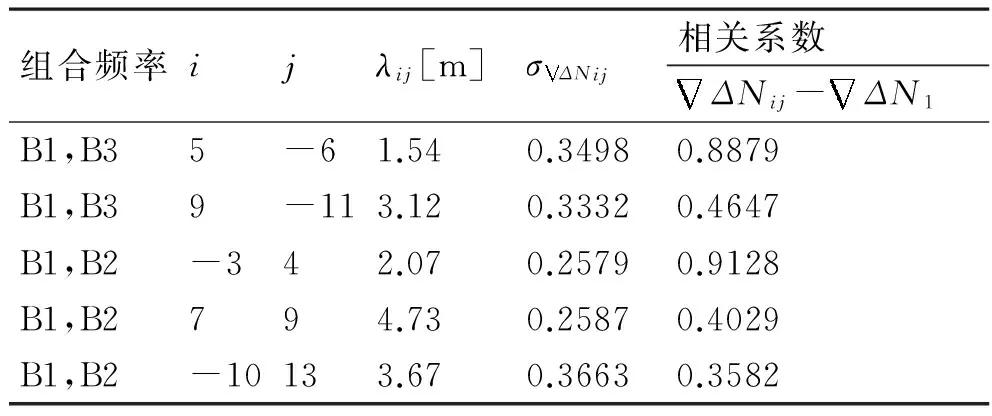
表1 几种北斗双频组合参数

5 结语

通过本文理论分析与研究数据表明,在观测时间较短的情况下,求解整周模糊度时,双差模糊度的搜索空间较大,通常是一个扁长度很大的椭球体,需要花费很多时间搜索,并且搜索的结果精度往往不高。通过采用线性组合的方式,选取适当的系数达到波长较长与观测标准差较小的双重标准时,组合观测值的整周模糊度要比直接计算单频B1或者B2的模糊度有更高的效率。利用两组或者多组合适的组合观测值,即如本文采取的几种组合来计算短基线B1和B2的整周模糊度,具有更高的正确性和稳定性,可以广泛地用于工程应用中。

[1] 邱蕾,花向红,蔡华,等.GPS短基线整周模糊度的直接解法[J].武汉大学学报:信息科学版,2009(1):97-99.

[2] 李征航,黄劲松.GPS测量与数据处理[M].武汉:武汉大学出版社,2009.

[3] 邢喆,王泽民,伍岳.利用模糊度聚类方法筛选GPS载波相位组合观测值[J].武汉大学学报:信息科学版,2006(1):23-26.

[4] 李卫军,姜卫平,王泽民.GPS载波相位三频组合观测值的模型研究[J].测绘信息与工程,2008(3):6-8.

[5] 李学逊.GPS载波相位观测值的线性组合及其相关性分析[J].测绘通报,1994(3):10-15.

[6] 刘超,王坚,路鑫,高井祥.GPS载波相位观测值随机模型的比较研究[J].测绘科学,2010(6):151-154.

[7] 赵亮,叶世榕,陈德忠,刘炎炎.组合观测值确定L1&L2的模糊度的探讨[J].测绘地理信息,2013(4):36-38.

[8] Melbourne W. G. The Case for Ranging in GPS-base Geodetic Systems. Rockville, Maryland[C]//Proceeding of the First International Symposium on Precise Positioning with the Global Positioning System,1985.

[9] Landau H, Euler H J. On-the-fly ambiguity resolution for precise differential positioning[C]//Proceedings of GPS-92. Alexandria Virginia: The institute of navigation,1992:607-613.

[10] CHEN D. Fast ambiguity search filter(FASF): a novel concept for GPS ambiguity resolution[C]//Proceedings of GPS-93. Alexandria, Virginia: The Institute of Navigation,1993:781-787.

Beidou Ambiguity Calculation by Double Frequency Combination Observation Value

CHEN Haiyue1WANG Jie2XU Guannan2

(1. Naval Aviation Insurance Repair Factory in Zhanjiang, Zhanjiang 524002) (2. Department of Navigation Engineering, Naval University of Engineering, Wuhan 430033)

Based on beidou dual-frequency combination, matrix change and the iterative process, a new iterative process is adopted with a linear combination of two different wave method. In a longer wavelength and lower ambiguity solution under the condition of correlation, the ambiguity search space is reduced and the fuzzy degree of calculating efficiency and speed are improved.

beidou dual-frequency, linear combination, ambiguity, ambiguity space

2014年12月6日,

2015年1月27日

陈海岳,男,工程师,研究方向:卫星导航。汪捷,男,副教授,研究方向:导航制导,定位方向理论与应用。徐冠楠,男,硕士研究生,研究方向:卫星定位和精密动态定位。

V474

10.3969/j.issn1672-9730.2015.06.013