基于微粒群算法的舰艇计划修理资源调度优化*
2015-03-14刘磊王平
刘 磊 王 平
(海军工程大学管理工程系 武汉 430033)
基于微粒群算法的舰艇计划修理资源调度优化*
刘 磊 王 平
(海军工程大学管理工程系 武汉 430033)
为解决舰艇修理计划中时间和资源制约带来的问题,提出了基于微粒群算法的舰艇计划修理资源调度优化方法。将不确定性多项式的求解问题转化为优先级搜索问题,并利用微粒群算法实现了问题的快速有效求解。工程实例的求解得到了合理有效的分配方案,解决了在资源制约下最小化工期的问题。
微粒群算法; 计划修理; 资源调度; 优先级
Class Number U674.7
1 引言
舰艇的修理受到时间和资源两方面的制约。当前舰艇计划修理中,由于承修单位同时承修多个项目,因而对于单个修理项目,其修理所配备的人力、物力等资源都是有限的。继而提出了在以缩短修理工期为前提的计划修理中如何优化调度有限资源的问题[1]。
计划修理资源调度优化是一个不确定性多项式求解问题,在工程管理方面现行的主要方法是关键路径法,但是该方法以时间最短为前提,无法满足资源条件的约束,容易出现资源超负荷的问题。
2 舰艇计划修理进度安排优化模型
一个舰艇修理工程由多个有序的修理项目构成,每个修理项目都有明确的工期要求以及资源需求。修理进度安排优化的目标是充分利用有限的资源,在尽可能短的工期内完成项目,每个项目进行过程中不能中断,寻优解为各个项目开始与结束的时间。
2.1 舰艇维修工程网络计划图
特定的舰艇修理工程中,各修理项目之间具有前后约束关系,即各修理项目有固定的开工先后顺序,将某修理项目之前需要完成的修理项目集合称为该项目的紧前修理项目,反之为紧后修理项目。通常,用网络计划图表达各维修项目之间的前后约束。
工程网络计划图的实质是有向无环图(Directed Acyclic Graph,DAG),可以用邻接矩阵表示。如图1所示,图1(a)为一个工程网络计划图,{x1,x2,…,x6}该维修工程所包含的六个维修项目。每个项目对应节点的父节点即为其紧前项目,子节点即为其紧后项目。为了统一工程开始和结束的时间,x1和x6为虚项目,所需工时为0。

图1 工程网络计划图及其邻接矩阵
2.2 舰艇计划修理进度安排数学模型
舰艇计划修理进度优化的目标是缩短工期,约束条件包括三项: 1) 修理项目顺序制约; 2) 各个修理项目的固定工期; 3) 各种资源限制。其数学模型可表达如下[2]:
mintN
s.t.ti-tj≥dj, ∀j∈Zi,i=1,2,…,N
(1)
(2)
其中,N为维修工程包含的项目总数,tN为维修工程的总工期。ti和tj为项目i和项目j的开始时间,di为维修项目i所需要的工期,Zi为项目i的紧前修理项目,m为维修需要的资源种类,rik为修理项目所需要第k类资源的数量,bk为维修工程所配备的第k类资源总量。
上述优化模型中,s.t.(1)隐含约束ti-tj≥0对应于前文的约束条件(1)和(2),表示紧后维修项目必须在紧前维修项目完成的前提下进行,并且项目工期必须足够。s.t.(2)对应于约束条件(3)为资源约束。
2.3 优化模型的转换
2.2节描述的数学模型是一个不确定性多项式(NP)问题,需要借助搜索算法寻找问题的解。对于特定的工程网络计划图,其网络结构确定,节点权值(项目完成时间)确定,因此可以转化为节点排序的次优求解问题。即将问题的求解转化为寻找一种项目的优先排序(优先级越高的项目,在资源足够的条件下,越先进行),使得在该顺序之下,维修工程的总计划工期最短。
由于每个项目的工期固定,为满足s.t.(1),只需保证紧前项目的优先级大于紧后项目,且紧前项目工期足够。由于工期所需资源固定,可将s.t.(2)转化为固定资源的分配,即一旦资源不足,优先级低的维修项目便需要等待前期项目完成再进行资源分配。
3 基于微粒群算法的优化搜索
微粒群算法(Particle Swarm Optimization,PSO)是由美国心理学家Kennedy和电气工程师Eberhart于1995年提出的一种模拟鸟类群体觅食行为的仿生智能计算方法[3~4]。PSO模型简单、易于实现、无需梯度信息并在各种连续型优化问题中表现出良好求解效果[5~8]。
微粒群算法的基本思想是通过群体中个体之间的协作和信息共享来寻找最优解。微粒群算法将每个个体看作是在n为搜索空间中的一个没有重量和体积的微粒,并在搜索空间中以一定的速度飞行,该飞行速度由个体的飞行经验和群体的飞行经验进行动态调整[9~10]。
3.1 PSO的搜索方案
(3)
设群体中微粒数为s,群体中所有微粒所经历过的最好位置为B(t),B(t)∈{P0(t),P1(t),…,Ps(t)},
T(B(t))=min{T(G1(t)),T(G2(t)),…,T(Gs(t))}
(4)
微粒群算法的进化方程可描述为
(5)
式中,下标“i”表示微粒的第i维,即第i个项目的优先级;“k”表示微粒k;t表示第t代;c1、c2为加速常数;为两个相互独立的随机函数。
3.2 目标函数的计算
维修工程需要的总工期是模型的优化目标,对于一个优化方案P,其工程的总工期T(P)的计算方法如图2所示。具体步骤如下:
Step1 初始化项目调度表,令T(P)=0,调度项目Xj指向虚项目X1。
Step2 查询调度项目Xj的紧后项目Sj。
Step3 查询Sj中优先级最高的项目。若该项目已调度过,转入Step2,否则转入Step4。
Step4 查询项目的紧前项目,若完成,转入Step5,否则转入Step3。
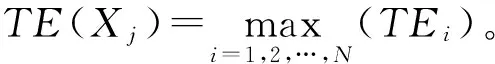
Step6 判断项目是否全部调度完毕,若未完成,存储已调度项目序号,并令j=j+1,转入Step2,否则,转入Step7。
Step7 令T(P)=TE(Xj)。
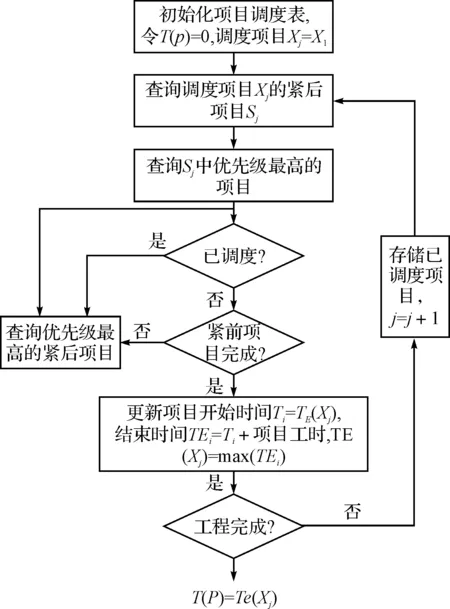
图2 总工期计算流程
4 实例
选取某舰艇维修工程实例部分计划进行优化分析。该工程所需人力资源包括电工、钳工和铜工三种,每天可调度人数分别为30、10、20。图3为该维修计划的工程网络计划图,表1为各个项目所需工期和资源。

图3 工程网络计划图
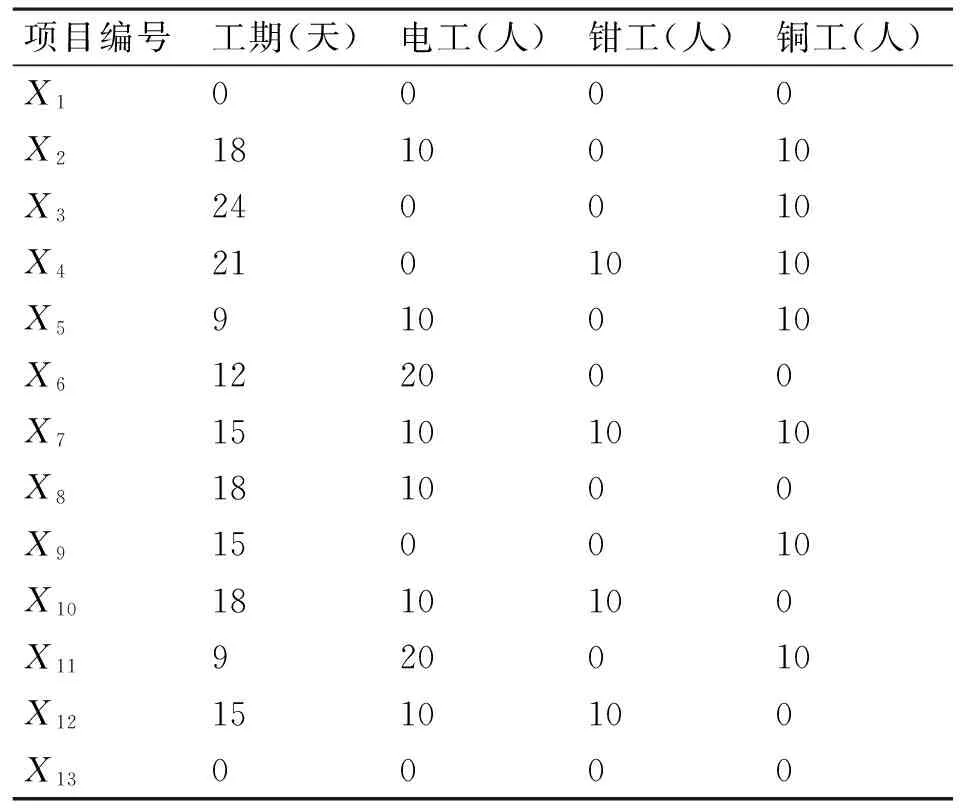
项目编号工期(天)电工(人)钳工(人)铜工(人)X10000X21810010X3240010X42101010X5910010X6122000X715101010X8181000X9150010X101810100X11920010X121510100X130000
为了满足微粒群体搜索范围的有效性,设定群体规模s为10,加速常数c1、c2均为0.5,采用Matlab2009R编程,Win7操纵环境,搜索结束条件为运行100代(t=100),或最优目标值保持不变10代。
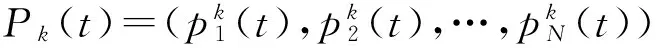
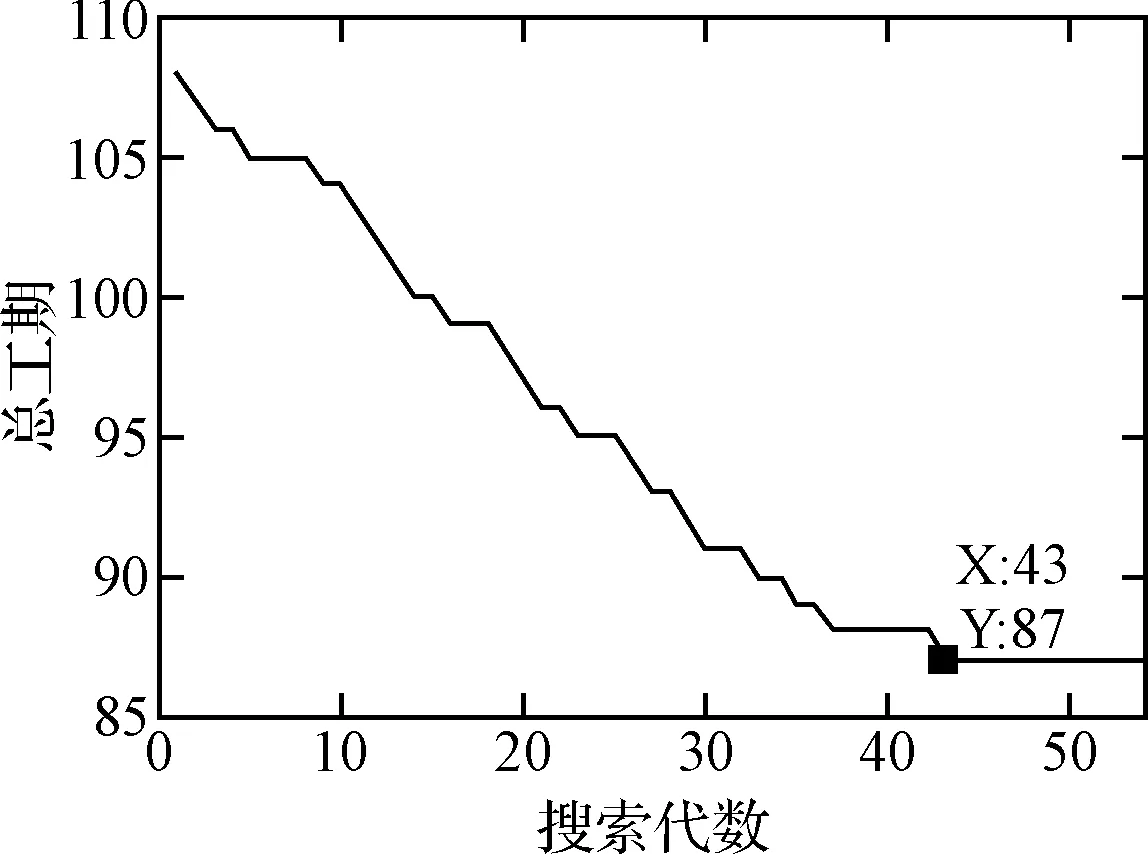
图4 优化搜索过程
图4为优化搜索的过程,如图所示,随着搜索代数的增加,维修工程的总工期(图中取值为所有微粒最好位置时的工期)逐渐缩短,优化呈现收敛态势。在第44代时到达最优维修工期87天,最优值保持10代到达54代时搜索停止。
根据总工期计算流程,可以得到修理工程计划调度如表2所示。
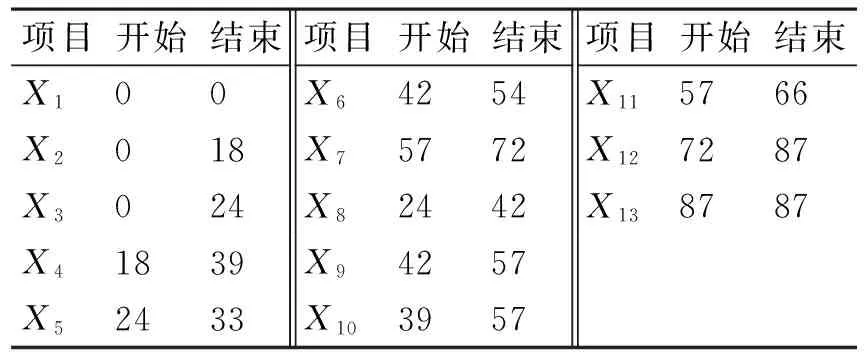
表2 修理工程计划调度表
5 结语
解决资源受限的计划维修项目调度问题,其难点是NP问题的寻优求解。本文将NP问题转化为优先级的寻优搜索,利用PSO算法求得调度方案。所研究方法具有一定的工程实用价值。
[1] 高健.船舶修理管理研究及信息系统开发[D].上海:上海海事大学,2007.
[2] 周世雷,郑映烽,刘子杨,等.舰艇计划修理资源约束性项目调度优化[J].四川兵工学报,2013,34(8):86-89.
[3] Kennedy J, Eberhart R C. Particle swarm optimization[C]//Proceeding of 1995 IEEE International Conference on Neural Networks. New York, NY, USA: IEEE,1995:1942-1948.
[4] 谢晓锋,张文俊,杨之廉.微粒群算法综述[J].控制与决策,2003,18(2):129-134.
[5] 沙立成,宋珺琤.基于改进粒子群优化LS-SVM的变压器故障气体预测[J].华北电力大学学报,2011,38(1):35-38.
[6] 朱童,李小凡,鲁明文.位置加权的改进粒子群算法[J].计算机工程与应用,2011,47(5):4-6.
[7] 赵志刚,常成.带变异算子的自适应粒子群优化算法[J].计算机工程与应用,2011,47(17):42-44.
[8] 任子晖,王坚.加速收敛的粒子群优化算法[J].控制与决策,2011,26(2):201-206.
[9] 梁昔明,董淑华.动态惯性权重和维变异的粒子群优化算法[J].计算机工程与应用,2011,47(5):29-31.
[10] 高浩,冷文浩,须文波.一种全局收敛的PSO算法及收敛分析[J].控制欲决策,2009,24(2):196-201.
Optimization of Resource-Constrained Ship Project Scheduling Based on PSO
LIU Lei WANG Ping
(Department of Management Engineering, Naval University of Engineering, Wuhan 430033)
To solve the problem caused by the time and resource constraints in the ship scheduled repair, the particle swarm optimization algorithm for resource scheduling is put forward. The problem of solving polynomial uncertainty is converted into priority search problem, and then the particle swarm algorithm is used to achieve a rapid and effective solving. The engineering examples has been solved reasonably and effectively, solving the problem of minimal with the chemicals resource constraints.
particle swarm optimization, scheduled repair, resource scheduling, priority
2014年11月19日,
2014年12月30日
刘磊,男,硕士研究生,研究方向:军事运筹、装备保障。王平,男,教授,硕士生导师,研究方向:指挥等。
U674.7
10.3969/j.issn1672-9730.2015.05.029
