基于Kalman滤波的激光陀螺系统极标定方法研究*
2015-03-14霍庚
霍 庚
(92941部队95分队 葫芦岛 125000)
基于Kalman滤波的激光陀螺系统极标定方法研究*
霍 庚
(92941部队95分队 葫芦岛 125000)
针对传统的分立标定方法标定精度受姿态基准精度的制约,且不满足带减振器的惯性测量单元(IMU)标定及现场标定的需求,提出一种基于Kalman滤波器的系统级标定方法。为了确保解的唯一性,该方法引入了基准坐标系的约束条件,以速度误差为观测量,对激光陀螺及加速度计相关误差参数进行最优估计及辨识。仿真结果证明该方法的有效性及可行性,满足高精度惯导系统的标定需求。
激光陀螺; Kalman滤波器; 系统级标定; 最优估计
Class Number U666.1
1 引言
目前国内精度最高的激光陀螺为机抖激光陀螺,为了隔离外界运动,保证机抖陀螺稳定可靠地工作,机抖陀螺惯性测量单元(Inertial Measurement Unit,IMU)一般通过减振器与载体相连[1]。传统的分立标定[2~5]方法需要依靠精密转台等设备提供高精度姿态基准,而减振器在标定过程中将产生一定的形变,间接地降低了姿态基准的精度,从而使标定精度降低。即使不存在减振器的情况,文献研究表明[6~9],基于精密转台等设备提供姿态基准的标定方法精度受设备自身精度的制约,如角秒级精密转台将引入同量级的安装误差标定误差,不能满足高精度姿态测量系统在高动态环境下的应用需求。另外,传统的分立标定方法需要精密转台等高精度姿态基准设备和隔振地基,一般只有实验室环境才能满足其使用要求,惯性测量单元在长期使用过程中如果需要维护、更换惯性元器件,将需要返回实验室进行重新标定,既很繁琐也很费时费力。因此,研究实现不需要高精度姿态基准且灵活方便的系统级标定方法是非常有意义的。
2 系统级标定Kalman滤波模型
2.1 参考系与惯性器件误差模型
在进行惯性测量单元标定时,首先必须指定一个惯性元器件的正交参考坐标系,基于精密转台的分立标定方法一般选取转台坐标性作为其参考系,系统级标定方法中没有转台系作为基准,必须作出新的约束[10]。本文建立了附加约束条件的陀螺和加速度计安装坐标系数学模型,在理想的情况下,要求三个陀螺仪的各敏感轴方向是互相正交的,并且与固联在其安装框架上的惯性测量参考系xryrzr一致,各加速度计的敏感轴方向也应该与参考系一致。
实际上,由于机械加工及装配工艺的限制,三个加速度计组成的加速度计坐标系xayaza和三个陀螺组成的陀螺坐标系xgygzg均不是正交坐标系,两者也不重合,标定实验的目的之一就是寻找这两个非正交坐标系到一个正交的参考坐标系的转换矩阵,这两个矩阵即陀螺和加速度计的安装误差阵Mg、Ma,分别表示为[5,11]
(1)
(2)
基于精密转台的分立标定方法一般选取转台坐标性作为其参考系,系统级标定方法中没有转台系作为基准,应该做出新的约束,这种约束是有效的且必要的,没有约束将导致安装误差标定的解不唯一。一种常用的定义惯性测量参考系的办法是令xryrzr系中的xr与xa即x加速度计的敏感轴方向一致,并且规定yr在oxaya平面内,然后根据右手系确定zr,此时ηxz、ηxy、ηyx均为零。加速度计安装误差表示式可改写为
(3)
激光陀螺IMU系统级标定是建立在误差方程基础上的,因此首先必须建立系统的误差模型。参考坐标系建立以后,考虑激光陀螺及加速度计常值漂移、刻度系数误差与安装误差,激光陀螺惯性测量单元中陀螺的输出误差方程可表示为[6,10~11]:
Δω=εb+δkgω+Mgω
(4)
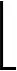
考虑加速度计零偏、刻度因子误差及安装误差,加速度计的误差输出方程表示如下:

(5)

2.2 Kalman滤波器设计
1) 状态变量的选取
本文选择以加速度计输入轴为基础确定参考坐标系,此时加速度计安装误差系数简化为三个参数,激光陀螺安装误差用共六个系数描述,此时用于系统级标定的Kalman滤波器状态变量选取如下,共27维:
(6)
2) 系统误差状态方程
在考虑各器件相关误差项的影响之后,系统误差方程表示如下[10~12]。
速度误差方程:
(7)
3) 观测量的选取
为了使标定算法不依赖于高精度姿态基准,本文研究仅以速度误差为观测量的系统级标定方法,姿态误差不可直接观测,在标定过程中只存在角运动,没有线运动,在没有惯性元件误差的理想情况下输出速度为零,本文选取观测量为Z=[δVEδVNδVU]。仅以速度误差为观测量的系统级标定方法的标定流程如下:惯性测量系统进入测量状态后,陀螺仪、加速度计的各误差量(刻度因子、安装误差、零偏)在设定的标定路径下得到激励,通过误差传播影响系统的解算输出,以速度解算误差作为观测量,通过设计的系统级标定用27维Kalman滤波器对各标定参数进行最优估计与辨识,从而完成标定过程。
3 仿真研究
3.1 参数设置
为了验证本文提出方法的有效性,对各误差参数进行充分的激励。参照实验室现有的某型机抖激光陀螺惯性测量单元实际的标定参数大小,按照合适的标定路径,利用C语言程序模拟产生了标定过程中的陀螺和加速度计数据,并根据误差状态方程设计了一个包含27维状态变量的Kalman滤波器,仿真参数设置如下所示:陀螺零偏(°/h):0.05/0.05/0.05,陀螺比例因子误差(10-6):100/50/100,陀螺安装误差(arcsec):-173.02/277.51/-31.65/82.26/-34.53/253.67,加速度计零偏(mg):0.05/0.05/0.05,加速度计比例因子误差(10-6):100/50/100,加速度计安装误差(arcsec):-217.00/382.30/-25.20
3.2 仿真结果及分析
按照上面的参数设置,运行仿真程序,得到陀螺及加速度计各误差参数估计结果。限于篇幅的原因,仅给出陀螺零偏及比例因子误差曲线图,如图1、图2所示。


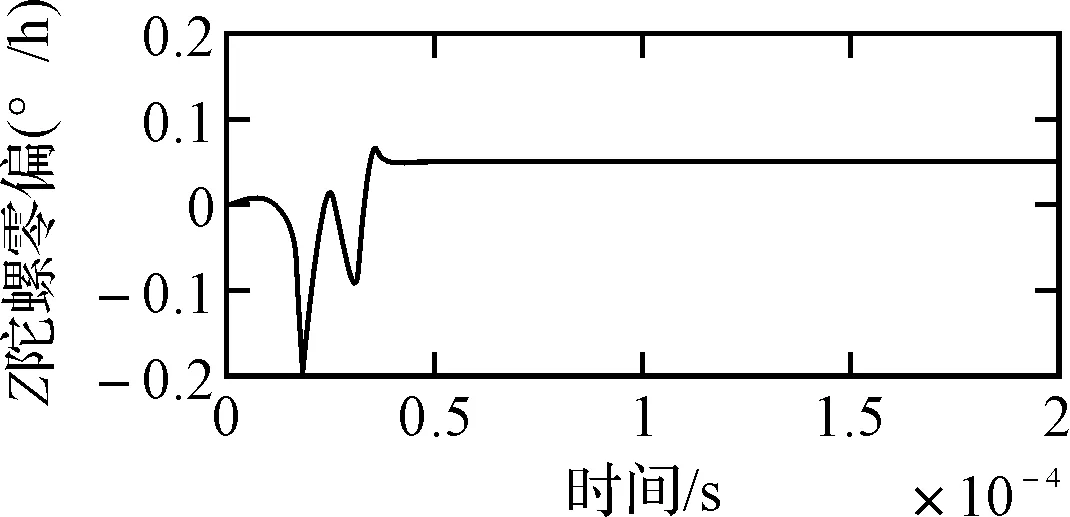
图1 各陀螺零偏标定结果
图1为各陀螺零偏标定结果,最终估计值为0.0515/0.0511/0.0492,参数精度优于0.005°/h;图2为各陀螺比例因子误差标定结果,最终估计值为99.8/50.1/100.2(10-6),参数精度优于0.5(10-6);陀螺安装误差(arcsec):-173.25/277.13/-31.99/81.4/-34.85/253.93,安装误差估计精度优于1″;加速度计零偏(mg):0.046/0.054/0.047,加速度计比例因子误差(10-6):99.8/49.6/100.2,加速度计安装误差(arcsec):-217.31/382.63/-25.52。从数据可以看出,陀螺和加速度计各标定参数均得到很好的估计,满足高精度惯导系统的标定需求。

图2 各陀螺比例因子误差标定结果
4 结语
本章研究了一种基于Kalman滤波并以速度误差为观测量的IMU系统级标定方法,指出不对参考坐标系进行约束将导致安装误差标定解的不唯一,引入了系统级标定方法基准坐标系的约束条件,推导了此约束条件下的安装误差表达式,使标定结果具有唯一解。推导了惯性测量单元的系统级误差参数标定Kalman滤波模型,此模型仅以速度解算误差为观测量,因而系统的标定精度不受转台精度的限制。通过理论分析及仿真研究表明,本文设计的标定路径及滤波算法在无需精密转台提供精确姿态基准的情况下,能准确估计出了激光陀螺惯性测量单元与陀螺相关的各误差参数。适用于带减振器条件和现场标定环境,标定精度不受转台精度的限制,适用于高精度惯导系统的标定。
[1] 王宇.机抖激光陀螺捷联惯导系统的初步探索[D].长沙:国防科技大学,2005.
[2] Rice H, Kelmenson S, Mendelsohn L. Geophysical navigation technologies and applications[C]//Position Loction and Navigation Symposium, PLANS2004, 26-29 April 2004:618-624.
[3] Zhang Hongliang, Wu Yuanxin, Wu Meiping, et al. A multi-position calibrationalgorithm for inertial measurement units[C]//AIAA Guidance, Navigation and Control Conference and Exhibit. Honolulu, Hawaii,2008.
[4] Bekkeng J K. Calibration of a novel MEMES inertial reference unit[J]. IEEE Transactions on Instrumentation and Measurement,2009,58(6):1967-1974.
[5] GUO Peng-fei, WANG Mei, REN Zhang, et al. The new calibration algorithm for the low-cost fiber-optics gyroscope[C]//Proceedings of the 2006 IEEE/ION Position, Location and Navigation Symposium,2006:739-743.
[6] 严恭敏,秦永元.激光捷联惯组的双轴位置转台标定仿真[J].中国惯性技术学报,2007,15(1):123-127.
[7] 白雪峰,赵剡.单轴速率三轴位置惯性测试转台误差及传递分析[J].航天控制,2006,24(2):26-29.
[8] 邓志红,刘亚辰,王清哲.转台角位置基准误差对激光捷联惯导标定的影响分析[J].中国惯性技术学报,2009,17(4):498-504.
[9] 肖桂平.光学陀螺捷联惯导系统的标定精度分析[D].长沙:国防科学技术大学,2008.
[10] 袁保伦,饶谷音.一种新的激光陀螺惯性测量组合标定方法[J].中国惯性技术学报,2007,15(1):31-34.
[11] 袁保伦.四频激光陀螺旋转式惯导系统研究[D].长沙:国防科学技术大学,2007:100-102.
[12] 刘锡祥,徐晓苏.惯性测量组件整体标定技术[J].中国惯性技术学报,2009,17(5):568-576.
Systematic Calibration Method for RLG Based on Kalman Filter
HUO Geng
(Unit 95, No. 92941 Troops of PLA, Huludao 125000)
The precision of traditional calibration method is limited by the attitude reference, and it doesn’t satisfy the IMU calibration with shock absorbers and field calibration requirements. So an systematic calibration method based on Kalman filter is developed in this paper. A restriction on the reference frame of RLG and acceleraters is added in order to make the calibration result exclusive, and this filter only uses the velocity errors as the observational vectors, and relative parameters of RLG and acceleraters are made optimal estimation and identification. The simulation results indicate that the method is so feasibal and effective that it could satisfy the requirements of high precision inertial navigation system.
RLG, Kalman filter, systematic calibration, optimal estimation
2014年11月8日,
2014年12月27日
霍庚,女,硕士,工程师,研究方向:惯性导航。
U666.1
10.3969/j.issn1672-9730.2015.05.012
