DOE技术在起重臂优化设计中的应用

侯云霞

(德州职业技术学院,山东 德州 253000)

DOE技术在起重臂优化设计中的应用

侯云霞

(德州职业技术学院,山东 德州 253000)

摘要：为提高某船用起重机起重臂结构刚度，减小其最大应力以及结构质量，首先对各变量进行灵敏度计算，去除对目标函数不灵敏的设计变量，以提高后续计算效率。基于DOE试验设计理论及有限元法构建优化问题的近似模型，借助拉丁采样对该近似模型拟合精度进行检验。基于遗传优化算法(GA)对该近似模型进行优化。优化结果表明：刚度提高9.4%，最大应力值减小21.4%，结构质量减轻9.3%。

关键词：结构优化； DOE； 遗传优化； 灵敏度； 起重臂

0引言

起重臂在起重机设计过程中是最主要部件之一，起重臂的研究已引起广泛关注[1]。在以往工程实践中，起重臂的设计大多为经验设计。对于桁架式的结构则选型相应的角钢进行连接，对于非桁架式结构大多采用厚金属板焊接而成。这种焊接式结构存在的问题是结构质量大，结构在工作时并不能使所有材料发挥其最佳性能，材料利用率不高。随着优化算法的不断进步，对这类结构进行优化设计成为可能。DOE(Design of Experiment)试验设计是一项以概率论、数理统计为理论基础的试验理论，能够科学地安排试验参数，以最少的试验次数获得准确的响应结果。目前常用的理论有Full Factorial，Fractional Factorial，Hammersley，Latin HyperCube，Plackett Burman[2-4]。本文将基于DOE设计理论对某起重臂结构钢板厚度进行优化设计，以提高结构刚度为目标函数，以质量和应力为约束，改进其性能。

1结构以及有限元模型

本文研究的起重臂高度为8 m，宽度为7 m，起重臂截面为一边长为60 cm的正方形梁结构，具体尺寸参数如图1所示。首先采用三维软件对结构进行三维建模，并利用Hypermesh对该起重臂结构进行有限元建模。由于本文后续对起重臂结构钢板厚度优化，实体单元并不能返回结构厚度参数，故选用四节点壳单元对起重臂结构进行有限元建模，选择单元边界尺寸为100 mm，最终有限元模型节点数为3 680，单元数量为3 675。结构材料为45号钢板，其弹性模量为200 GPa，泊松比为0.3，材料密度取为7 800 kg/m3，有限元模型如图2所示。

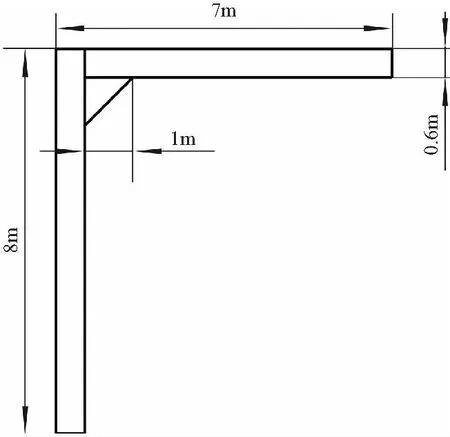
图1　起重臂结构Fig.1　Boom structure

图2　起重臂有限元模型Fig.2　Finite element model of the boom

2DOE优化流程

DOE优化流程如图3所示。其优化流程可大致描述为：根据DOE采样理论对结构钢板厚度设计空间进行科学采样，通过有限元软件二次开发的方法，将采样值植入fem求解文件，将求解文件提交有限元求解器，并返回结构目标函数以及约束的响应值。根据样本点以及对应的响应值构建优化问题的近似模型，并基于该模型采用优化算法对齐进行搜索。这种方法的优势在于，不需要对原模型进行搜索，因为搜索算法的局限性，有很多搜索歩会陷入无效搜索过程，反而对原模型进行返回响应值会浪费大量的计算时间。构建优化问题的近似模型可以使得优化算法在优化过程中只针对优化近似模型进行搜索，而不从原模型返回响应值，采用近似模型返回响应值速度较快。

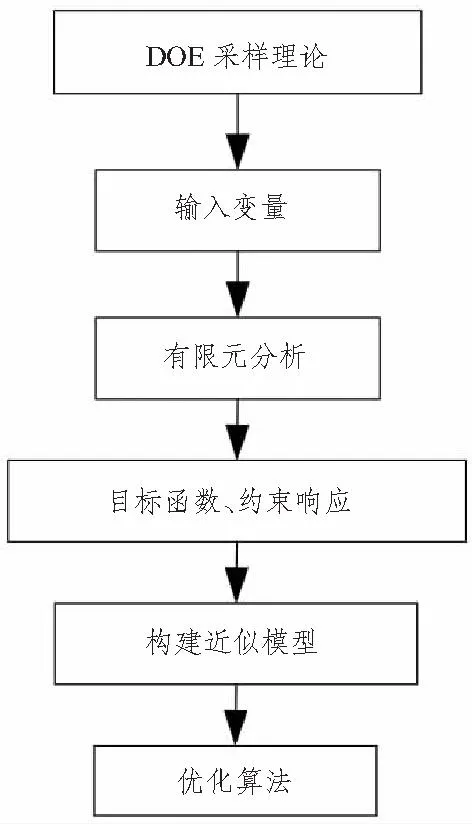
图3　DOE优化流程Fig.3　DOE optimization process

3灵敏度计算

为仔细研究起重臂结构，将起重臂每块钢板厚度均作为设计变量进行考虑。各设计变量编号如图2所示。共有10个设计变量，个数较多，然而并不是所有的设计变量均对结构目标函数较为灵敏，可能在后续的优化过程中浪费计算时间。因此本文基于Plackett Burman试验设计理论对设计空间进行采样,样本点如表1所示。通过二次开发方法将这些样本点嵌入fem有限元求解文件，提交给有限元求解器，并提取其响应值。各样本点返回的结构刚度、最大应力及结构质量列于表1。对表1的设计变量以及其响应值进行灵敏度分析，分析每个变量对结构刚度、最大应力、结构质量的灵敏程度，结果列于表2。可以看出，变量1设计厚度对结构刚度、最大应力以及结构质量均不灵敏，表明后续对该变量研究意义不大，故将该变量去除。最终只对变量2~10进行研究。

表1　Plackett Burman采样数据

表2　设计变量灵敏度

4近似模型构建

构建近似模型分为2个步骤：1)基于Hammersley采样理论对设计变量2~10的设计空间进行采样，根据样本点通过有限元过程返回结构的响应值，并拟合优化问题的近似模型；2)基于Latin HyperCube采样理论对设计变量2~10设计空间进行采样,同样地借助有限元过程返回其响应值。Hammersley采样得到的样本点以及其响应值列于表3。由于采用不同的理论，得出的样本点也不同，限于文章篇幅，Latin HyperCube采样得到的样本点本文并未给出。采用Latin HyperCube对设计空间采样是为了验证拟合得出的近似模型的正确性。使近似模型返回该样本点的响应值，并与样本点有限元过程返回响应值对比于表4。对比发现，近似模型返回的响应值与有限元模型返回的响应值相对误差较小，尤其是结构质量的误差几乎为0，说明该近似模型具有较好的可靠性。

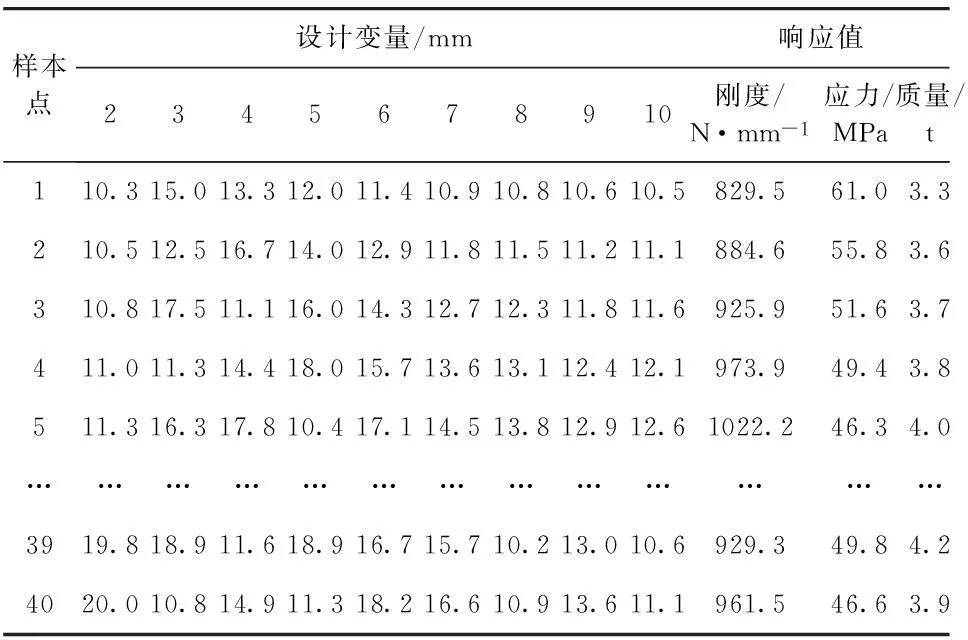
表3　Hammersley采样数据

表4　近似模型误差

5结构优化

遗传算法是模仿生物进化过程的一种算法，具有较好的鲁棒性，不管是线性问题还是非线性问题，均具有较好的收敛性。对于给定的收敛精度，能够以较少的搜索时间达到计算要求。本文将基于遗传算法对该近似模型进行优化，在优化过程中，取最大计算步数为200，最小搜索歩数为25，种群数量取50，变异率取为0.01，随机因子取为1，惩罚因子取为2，分布系数取为5，收敛精度为0.001。初始结构刚度为1 135 N/mm，最大应力值为44.3 MPa，结构质量为4.3 t。在该优化中，目标函数为最大化结构刚度，约束条件为结构最大应力不超过35 MPa，并且结构质量不超过3.9 t。结构刚度、最大应力、质量的搜索过程如图4~图6所示。优化经过27次搜索以后得到最优化结构。

图4　刚度迭代历程Fig.4　Iterations of the stiffness

图5　应力迭代历程Fig.5　Iterations of the stress

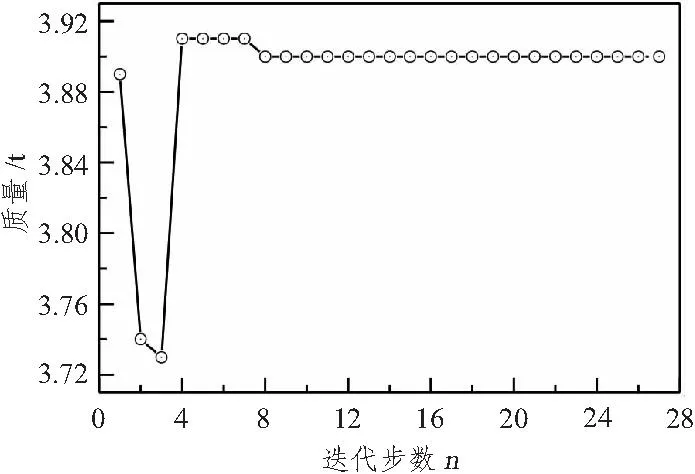
图6　质量迭代历程Fig.6　Iterations of the mass

最终优化结果为：变量1~10的厚度依次为10 mm，10.01 mm，10.00 mm，10.00 mm，10.00 mm，19.96 mm，15.13 mm，20.00 mm，10.87 mm，20.00 mm。优化得到的结构刚度为1 241.82 N/mm，结构最大应力值为34.82 mm,得出的结构质量为3.9 t。

相比初始结构，优化得出的结果刚度提高了9.4%，最大应力值减小了21.4%，结构质量减轻

9.3%。由于优化只正对结构钢板厚度进行研究，对结构的拓扑结构以及形状均不影响，加工时只需选型不同厚度钢板便可实现。

6结语

1)建立了某船用起重机起重臂有限元模型，并借助二次开发的方法使得有限元模型厚度参数化研究。

2)借助各种DOE试验设计理论，对各设计变量进行了科学的采样并提交有限元过程。通过样本点以及其响应值，基于最小二乘理论拟合得到了具有较高精度的优化近似模型。

3)基于遗传优化算法对近似模型进行了优化搜索。结果表明，相比初始结构，优化得出的结果刚度提高了9.4%，最大应力值减小了21.4%，结构质量减轻9.3%。由于优化只正对结构钢板厚度进行研究，对结构的拓扑结构以及形状均不影响，加工时只需选型不同厚度钢板便可实现。

参考文献：

[1]王阳.船用起重机防摇装置设计研究[J].舰船科学技术,2013,35(7):105-108.

WANG Yang.Research and design of an anti-swing mechanism for a shipborne crane[J].Ship Science and Technology,2013,35(7):105-108.

[2]HINRICHS A.Discrepancy of hammersley points in besov spaces of dominating mixed smoothness[J].Mathematische Nachrichten,2010,283(3):478-488.

[3]刘刚,钟小军,董鹏,等.基于遗传算法和神经网络的舰船电子装备备件优化模型研究[J].舰船科学技术,2008,30(5):138-142.

LIU Gang,ZHONG Xiao-jun,DONG Peng,et al.Research on warship electronic equipments spare parts optimize model based on genetic algorithm and neural network[J].Ship Science and Technology,2008,30(5):138-142.

[4]王爱岭,何祖军.基于遗传算法的舰船破舱浮态调整措施优化研究[J].舰船科学技术,2010,32(3):29-31.

WANG Ai-ling,HE Zu-jun.A study on righting measure optimization in damaged ship floatation adjustment based on genetic algorithm[J].Ship Science and Technology,2010,32(3):29-31.

The application of the DOE technology in boom optimal design

HOU Yun-xia

(Texas Vocational Technical College,Dezhou 253000,China)

Abstract：In order to improve a marine crane boom′s structural rigidity and reduce its maximum stress and mass. Firstly, the objective function sensitivity of each variables are calculated, the design variables insensitive to the objective function are then removed in order to improve the efficiency of the subsequent calculations.Approximate model of the optimization problem was established based of the DOE test design theory and the finite element method, and the fitting accuracy of the approximate model was then tested with Latin sampling. The optimization was the carried out with the Genetic Algorithm (GA). The optimization results show: the stiffness of the optimal structure increased by about 9.4%, maximum stress value decreased by about 21.4% and mass decreased by about 9.3%, this study provide a guide for the similar design.

Key words：structural optimization;DOE;genetic optimization;sensitivity;boom

作者简介：侯云霞( 1972 - ) ，女，副教授，从事机械制造、数控技术教学工作。

收稿日期：2014-06-18； 修回日期： 2014-10-10

文章编号：1672-7649(2015)02-0180-04

doi：10.3404/j.issn.1672-7649.2015.02.040

中图分类号：U653.921

文献标识码：A