某船用风力发电机叶片降噪设计

桑露萍

(潍坊科技学院,山东 潍坊 262700)

某船用风力发电机叶片降噪设计

桑露萍

(潍坊科技学院,山东 潍坊 262700)

摘要：为降低风力发电机叶片噪声，探索从形貌优化到降低风叶噪声的解决方案。根据薄壁结构高刚度形貌优化以提高某阶模态频率为优化目标的特点，通过对风叶结构模态分析，为形貌优化确定合适的目标模态。以风叶几何形状作为设计变量，体积作为约束函数，第一阶固有频率作为目标函数，对风叶结构进行了形貌优化。优化结果表明：改进后风叶第一阶固有频率值由42.3 Hz提高到57.6 Hz，提高了36.2%。在相同的激励下，优化得出的结构具有更多的振动衰减时间，从而达到减少振动以及噪音的目的。

关键词：形貌优化；有限元；风力发电机；噪声

0引言

风力发电是技术成熟，具有大规模发展潜力的可再生能源。目前该技术在舰船设备上已有所应用[1]。舰船噪声作为其使用性的一个重要指标开始受到越来越多的关注[2]。因此，风力发电机的振动噪声控制成为发电机结构设计领域的又一热点。

风力发电机是由薄板制造而成，刚度小，面积大，很容易与跟它相连的船体部件发生共振，辐射噪声较大。因此，有效降低风力发电机叶片噪声成为风力发电机优化设计的重要目标。舰船振动和噪声控制一般从降低噪声源与控制噪声传播途径两方面进行。目前，在控制噪声传播途径方面已有较多的应用研究, 但其研究对象多集中于阀、管路等结构[3-5]。抑制噪声源方面的应用研究仍然较少。

随着各种优化算法的不断完善，出现了一些新的优化设计方法。其中形貌优化是一种形状最佳化的方法，即在板壳结构中寻找最优的加强筋分布的方法来改变结构的频率与强度。由于风叶结构为薄壁结构，以往在工程实践中提高风叶结构频率减少振动以及噪声往往是通过增加脊梁的方法，但是这样会使得风叶结构质量大幅增加，增加成本的同时也会使得风叶工作可靠性降低。采用形貌优化对风叶结构进行优化得出的结果，大多可采用冲压工艺实现，该方法对结构的质量影响很小，并且对于已经成型的产品，仍然有较大的改造空间。本文将基于形貌优化方法，结合结构模态分析，为风叶结构形貌优化选择合适的目标函数进行优化。

1有限元模型建立

某船用风力发电机结构如图1所示，主要由6片风叶组成，每片风叶通过2个风叶支架与风力发电机壳体进行连接。风叶有薄钢板冲压而成，成为一直径为220 mm的半圆筒状结构，长度为1 200 mm。为简化问题，本文采用Ug软件对其中一片风叶进行三维建模，并采用Hypwemesh对叶片结构进行网格划分。建立有限元模型前，首先借助CAD软件对几何结构进行清理。由于工艺上采用的小孔以及倒角对计算精度影响较小，在有限元模型中不予体现，从而有效简化有限元模型，节省计算精度。由于风叶为薄壁特征，采用壳单元进行描述，定义单元类型为CTRIA3和CQUAD4的混合单元，即在划分中以CQUAD4为主，CTRIA3不超过总数的5%。最终划分节点数为36 383,单元数为35 930，建立的有限元模型如图2所示。风叶结构材料为45号薄钢板，其弹性模量为200 GPa，泊松比为0.3，材料密度取为7 800 kg/m3。

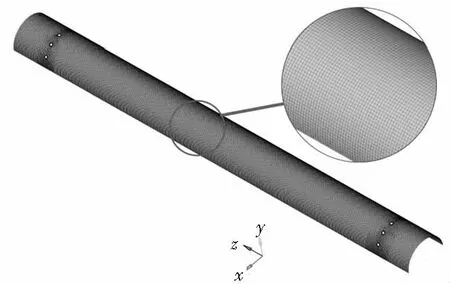
图2　风叶有限元模型Fig.2　Finite element model of the blade

其中风叶与风叶支架连接部位一圈采用reb-2单元进行描述，并对reb-2单元进行单点约束6个自由度，有限元模型边界条件如图3所示。

图3　有限元模型约束条件Fig.3　Constraints

2形貌优化

形貌优化是一种形状最佳化的方法，该方法可以在结构中找出加强筋的最佳位置，来提高系统的固有频率，间接提高结构刚度。形貌优化数学模型可表述为：

S.T.gi(X)≤0，(j=1,2,…,m)，

式中，X=x1,x2,…,xn为设计变量；F(x)为目标函数；gj(X)为不等式约束函数；上角标L和U分别为设计变量下限与上限。

式中：VOL1为形貌优化前叶片体积；VOL2为形貌优化后叶片体积。取g1(X)≤1.1，即优化后的叶片体积不能大于优化前的1.1倍。

目标函数F(x)为枪管结构的某阶模态频率值，该频率值在优化过程中将被最大化，来提高枪管刚度。在此，目标函数F(x)与优化前后枪管结构体积VOL1、 VOL2为有限元分析过程返回的结构响应函数。Optistruct软件允许用户自定义各种响应函数，使得该形貌优化顺利进行。OptiStruct使用迭代的程序，通过逼近的方法来求解优化问题，其提供的形貌优化方法可以对静力、模态、屈曲、频响等分析过程进行优化，优化流程如图4所示。

优化流程可大致描述为：有限元求解器首先对fem文件提交的网格以及单元信息，进行刚度矩阵的组装。并将边界条件一同提交给有限元模型求解器，通过有限元求解，返回各单元的响应值，将响应值与设计给出的收敛要求进行对比，如果满足收敛要求，则停止搜索，返回最优解。如果不满足收敛条件，则对结构进行灵敏度计算，将对于目标函数灵敏的单元进行设计并优化，对于优化的结构重新组装其刚度矩阵，并返回其响应值再与收敛要求进行比较。并重复上述步骤，直到满足收敛要求为止。

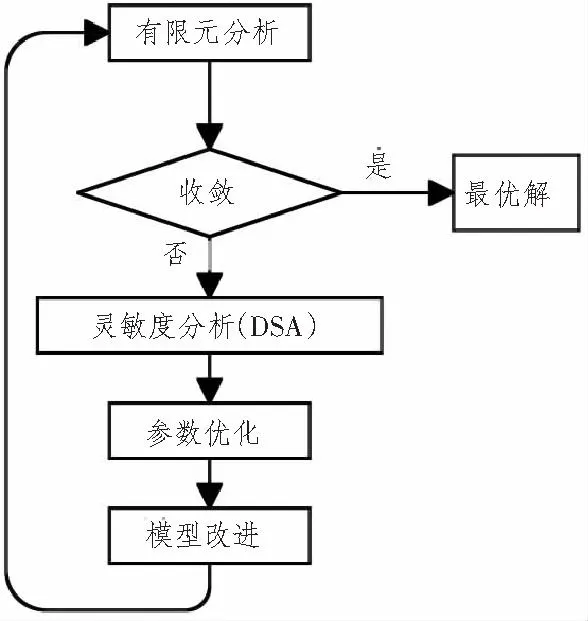
图4　优化流程Fig.4　Optimization process

2.1　目标函数选取

形貌优化方法是基于对结构某阶模态频率最大化为目标的优化求解，优化得到的结构在该频率附近的刚度将得到加强，因此对结构模态的选择对优化结果有着决定性的影响。

风叶结构由薄钢板压制而成，并且风叶支架与风叶连接处相距较远。风力发电机在工作时，风叶在风载激励下很容易发生低频振荡，从而辐射出噪声影响人员舒适性。

因此，需要对风叶结构进行模态分析，并结合风力发电机振动情况选择叶片模态数作为目标函数，使得优化出来的叶片结构能够在工作时具有较高的动刚度，降低噪音。

对于一个n自由度线性定常系统，其运动方程可写成：

Mz··+Cz·+Kz=p。

式中：M，C，K分别为结构质量、阻尼和刚度矩阵；z··，z·， z和p分别为系统各点加速度响应向量、速度响应向量、位移响应向量和激励力向量。

由于模态分析求解的是固有频率和振型参数固有模态，与外载荷无关，取p=0。忽略结构阻尼的影响，运动方程可表示为：

Mz··+Kz=0；

则特征方程可表示为：

式中：ωi为第i阶模态固有频率值；n为自由度系统有n个固有频率。

对于矩阵阶数超过1 000的大型问题，子空间迭代法、Ritz向量法和Lanczos法被公认为求解部分低阶极端特征值和特征向量的有效方法。本文采用Lanczos法进行求解，采用eigrl关键字调用该子程序对风叶有限元模型进行模态分析，提取其前6阶模态，结果如图5所示。

图5　风叶结构振型Fig.5　Mode shapes of the blade

由于风叶在工作过程中，主要体现为横向振动。通过对比模态分析结果，风叶前六阶模态振型，其中第1阶模态振型主要为风叶结构的横向振动，故在该优化中取第一阶模态作为目标函数。

2.2　形貌优化

风叶与风叶支架配合处结构采用螺栓连接，该部分由于连接的需要结构不能在优化过程中发生变形。为此将各螺栓孔周围单元作为非设计区域，其余部分为设计区域，二者在图中通过不同颜色区分，如图6所示。非设计区域在计算过程中不会发生变化。而设计区域会在计算过程中发生变形，以使得风叶的一阶频率最大化，来提高风叶结构的刚度。

图6　设计与非设计区域Fig.6　Design and no-design domains

为了使得优化出来的风叶结构易于加工，约束壳单元的变形均沿着风叶结构表面法线方向，且变形量小于8mm。通过eigrl关键字提取枪管的第一阶频率值，并将其定义为目标函数。定义优化后与优化前枪管体积比作为约束函数，约束其值小于1.1。由于在优化过程中，随着单元形状变化结构频率与振型有可能阶次发生交错，因此在优化过程中定义了param、modetrak关键字来反复对比结构振型来追踪结构模态频率，使得结构优化能够顺利进行。形貌优化模型经过15次迭代以后达到收敛，风叶结构优化结果云图如图7所示。同时为了使得优化出来的结构易于加工，本文在有限元模型中设置了1-psym关键字控制设计变量的对称性，使得优化出来的结构对称于风叶结构中心面。每个优化过程具有3个要素：目标函数，设计变量，以及约束。本文在设计变量的上限设置中已将其下限设为0，其上限设为8mm，以使得加工能够顺利进行，故在后续设置中不需设置其约束条件。

图7　形貌优化结果Fig.7　Topography optimization results

由于风叶为薄壁结构，可采用冲压工艺实现，容易实现，该优化结果有一定参考价值。

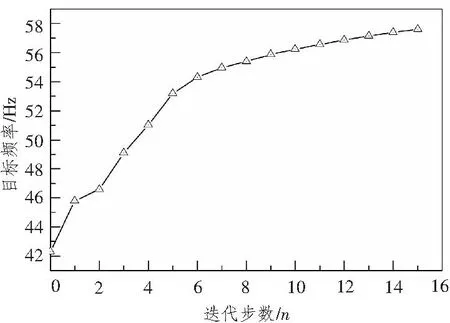
图8　目标函数迭代结果Fig.8　The objective function iteration results

优化过程中，优化搜索算法有可能陷入局部最优解，从而使得优化出来的结构不是全局最优，这样优化出来的结构并不能发挥其最佳性能。为此，采用Optistruct软件提供的opticontrol关键字进行控制，本文将opticontrol关键字值设为0.001，以避免优化搜索程序过早结束搜索过程，最终优化在迭代15歩以后停止搜索，得出结构在以一阶模态为目标函数情况下的最优解。目标函数迭代过程见图7，风叶结构第一阶模态频率值为42.3Hz，频率值提高为57.6Hz，相比原始结构频率提高了36.2%。相比原始风叶结构，优化得出的结构在相同的激励下，会有更多的振动衰减时间，从而达到减少振动以及噪声的目的。

3结语

1)通过对某船用风力发电机叶片进行模态分析，为形貌优化找到了合适的目标模态。优化后的叶片目标模态频率由42.3Hz提高到57.6Hz，提高了36.2%。相比原始风叶结构，优化得出的结构在相同的激励下，会有更多的振动衰减时间，从而达到减少振动以及噪声的目的。

2)优化得到的结构为风叶表面凸起的筋特征，由于风叶为薄壁特征，可采用冲压工艺进行加工，优化结果具有较好的工艺性。

3) 形貌优化是一种形状最佳化优化算法，其优化出的结构便于冲压加工。结合结构模态分析，能够为优化过程选择较优的目标函数，从而使优化出的结构能够发挥最佳性能。本文提出的方法具有一般性意义，同样可以应用于其他机械结构设计。

参考文献：

[1]叶志浩,方明,马凡,等.舰船综合电力系统发电机组投切条件分析[J].舰船科学技术,2012,34(10):49-52.

YEZhi-hao,FANGMing,MAFan,etal.Theprincipleofgeneratorunitsswitchingon/offinnavalvesselintegratedpowersystem[J].ShipScienceandTechnology,2012,34(10):49-52.

[2]仇远旺,王国治,胡玉超,等.舰船振动噪声的快速预报技术[J].舰船科学技术,2011,33(11):89-93.

QIUYuan-wang,WANGGuo-zhi,HUYu-chao,etal.Researchonfastpredictmethodforvibrationandunderwaternoiseofwarship[J].ShipScienceandTechnology,2011,33(11):89-93.

[3]吴石,张文平,封海波,等.充液管路系统中阀门流噪声的研究[J].噪声与振动控制,2005,25(3):51-53,57.

WUShi,ZHANGWen-ping,FENGHai-bo,etal.Studyonflownoiseofvalvesinfluid-filledpipplinesystem[J].NoiseandVibrationControl,2005,25(3):51-53,57.

[4]徐洋,华宏星,张志谊,等.舰船主动隔振技术综述[J].舰船科学技术,2008,30(2):27-33.

XUYang,HUAHong-xing,ZHANGZhi-yi,etal.Summaryofshipactivevibrationisolationsystem[J].ShipScienceandTechnology,2008,30(2):27-33.

[5]程晶,那建,杨会金,等.舰船设备振动监测阈值设定方法[J].舰船科学技术,2012,34(11):68-70,116.

CHENGJing,NAJian,YANGHui-jin,etal.Approachtothresholdingvibrationmonitoringofon-boardmachinery[J].ShipScienceandTechnology,2012,34(11):68-70,116.

A wind turbine blade noise reduction design

SANG Lu-ping

(Weifang University of Science and Technology,Weifang 262700,China)

Abstract：A topography optimization approach was proposed to reduce the noise of the wind turbine blade. As increasing one mode frequency was the high rigidity optimization objective for topography optimization, appropriate optimization objective was determined by conducting a modal analysis. Considering the blade shape as design variables, volume as constraint function, and maximize the first mode as objective function of the topography optimization using optistruct. The results show that the first order natural frequency increased by 36.2%. The optimized blade structure will have more vibration decay time under the same excitation, so as to achieve the purpose of reducing vibration and noise.

Key words：topography optimization;finite element method;wind turbine blade;noise

作者简介：桑露萍( 1970 - ) ，女，讲师，研究方向为机械设计与制造。

收稿日期：2014-07-08； 修回日期： 2014-11-12

文章编号：1672-7649(2015)02-0156-04

doi：10.3404/j.issn.1672-7649.2015.02.034

中图分类号：TK83

文献标识码：A