风电场集电线路路径优化研究

刘军，刘庆超，魏超

风电场集电线路路径优化研究

刘军1，刘庆超2，魏超2

（1.华电新疆发电有限公司，新疆乌鲁木齐830063；2.华电电力科学研究院，浙江杭州310030）

风电场集电线路路径直接影响工程造价，因此如何选择合理的路径对于控制工程造价，提高风电场效益具有至关重要作用。本文提出“集电线路全寿命周期运行费用最小”的思想，通过分别建立如下模型：线路投资费用折现函数模型、不同截面及长度线路造价模型、线路长度与线损造价模型、线路回数与造价模型，从而可以实现集电线路路径优化，为投资者及设计人员提供最佳路径方案。

粒子群算法；集电线路；路径优化；遗传算法

0 引言

风电场集电线路设计过程中，路径优化及导线选型不仅对工程造价有较大影响，而且还影响着运行后的线路损耗等收益指标，因此集电线路导线选型及路径优化相关研究对于提高风电场的设计水平具有重要意义[1-3]。主要集中在设计方面，如：集电线路电缆选型，主要通过研究连接风机台数及通过电流的大小，从而选择合适的电缆型号；线路整体设计，主要从设计条件出发，针对杆塔分析、导线型号、导线安全系数、防雷及接地等因素进行考虑；接线方式的研究，主要也是从设计角度出发，对如何能够完成及达到预期标准进行完整设计。以上研究并没有从风电场节约成本及提高效益角度出发，进行技术经济比较。

因此本文提出基于“全寿命周期费用最小”思想对集电线路路径进行优化，针对目前风电场集电线路路径选择的主观性和不合理性，运用优化理论对其进行理论计算分析，从而确定最佳路径，解决影响集电线路工程造价的决定性问题，达到经济效益最优的目的。

1 集电线路路径优化模型

1.1 线路投资费用折现函数

线路投资费用应计算比较资金的等年值，由于该部分费用在工程项目的前期支付，因此应考虑资金的时间价值。线路投资的现值和等年值的转换系数按下式计算。计算公式如下：

式中K—现值和等年值的转换系数；

r—资金贴现率；N—分摊年限。

1.2 不同截面及长度线路造价影响模型

1.2.1 截面面积计算模型

风电工程与一般的电网工程不同，风电场的出力受环境、风资源的变化的影响。风电场一般采用架空集电线路方式，存在对导线截面的选取的问题[1]。

对于拥有较大导线截面的架空线路，虽然风电工程一次投资较大，但由于运行中电能损耗较小，因此能降低运行费用。反之，若导线截面较小，虽能使工程造价降低，但会增加其运行费用。因此对风电场架空线路来说，存在导线截面的最佳选择的问题。导线截面应按“经济电流密度”来选择，也就是指年运行费用最低时所对应的电流密度。年运行费最小时所对应的截面积，称为经济截面积。经济电流密度值Ij见表1。

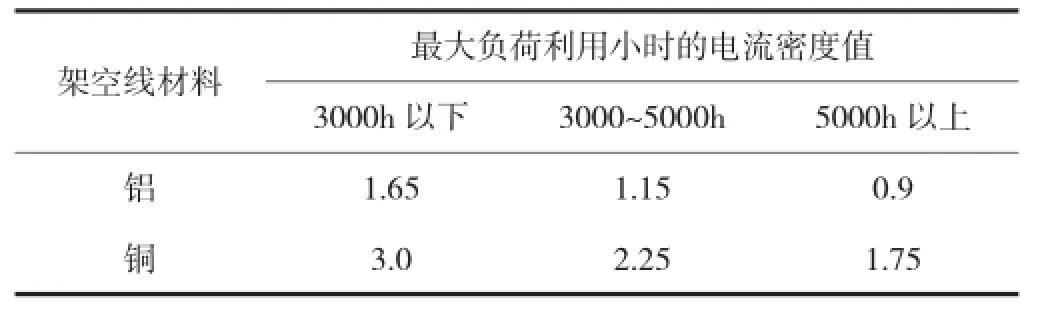
表1 经济电流密度

目前，国内风电场通常年运行小时数小于3000h，极少风电场年运行小数为3000～5000h，线路类别通常为钢芯铝绞线，因此最大负荷利用小时的电流密度值为1.65或1.15。

当已知经济电流密度和线路最大工作电流时可计算出经济截面积Sj，即：Sj=Ig/Ij。Ig为计算工作电流，由下式计算得到：

式中Igm—第m条集电线路计算工作电流，A；

Pi—第i台机组功率，kW；

α—功率因数；

U—集电线路电压等级，kV；

n—风机台数，也可表示集电线路回数。

因此第m条集电线路截面面积为：Sjm=Igm/Ij。

1.2.2 线路长度计算模型

线路长度指不同回数线路连接各个风机至升压站线路的总长度。

通常各个风机位置及升压站进线点的坐标为（x，y），因此两点间的距离为[5，6]：

式中l—（xi，yi）与（xi+1，yi+1）两点间的距离。因此计算单条集电线路长度模型如下：

式中lm—第m条线路总长度，km；

x0，y0—升压站进线点坐标；

xi，yi—第m条线路连接的从升压站至各个风机点的顺序坐标，其中i，j=1……n。

1.2.3 线路截面、长度与线路造价函数模型

根据《电力装置性材料价格》（2006年版）提供的不同型号架空线价格，可建立截面面积与线路造价的函数模型，如下[7]：

式中A—线路总投资，元；

m—线路回数；

Am—第m条线路总投资，元。

1.3 线路长度与线损函数模型

线损是电能在电力网传输，分配过程中客观存在的能量损失现象。集电线路线损主要因素是：各线路中箱变出线至开关柜进线之间线路的电能损失。计算公式如下[8～10]：

式中P—线路年损耗；

Rm—第m条线路电阻，Ω；

h—年运行小时数。

式中rm—第m条线路每千米电阻。

1.4 线路回数与造价函数模型

线路回数的多少影响接入升压站中的开关柜数量，通常线路1条，进线1条，其相关函数如下：

式中Cm—线路为m条时开关柜总造价，元；

c—单台开关柜价格，元。

1.5 集电线路规划模型

根据以上各个函数模型，可以建立集电线路路径优化模型，其数学描述如下：

式中F—总费用，不同回路集电线路投资费用的等年值和年线损费用之和；

B—电价，元/kWh。

2 基于遗传算法混合粒子群算法的风电场路径优化

2.1 基于粒子群的混合遗传算法描述

传统PSO（Particle Swarm Optimization）算法公式如下[11]：

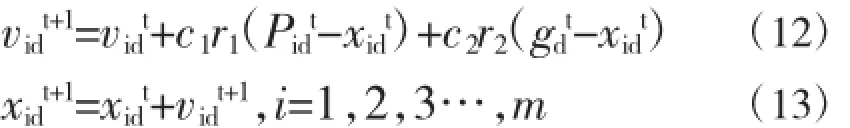
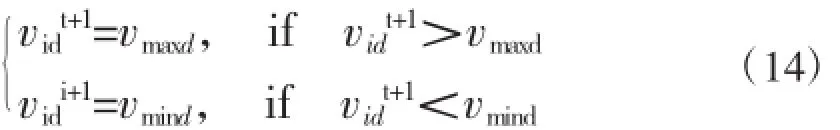
对传统PSO算法引入GA算法后的主要变动如下[11，12]：

交叉操作：将用粒子历史最优和粒子当前做交叉，如果得到的结果更优，则更新粒子，否则保持粒子当前状态。再用粒子群最优和粒子当前做交叉，如果得到的结果更优，更新粒子，否则保持粒子当前状态。

诱导矩阵：诱导矩阵的作用是，诱导粒子的变异方向。诱导矩阵为（34，K）型，行数即为诱导粒子的维数，即对每个风机及升压站进行诱导。列表示诱导的结果，对于某行的任一列的值，表示该行标号的风机，下一连接的风机的可能编号。列如：K取5，第i（i为1～34的值）行为（3，5，7，8，2），则可以看出风机i后面连接风机3的概率最大，其次是5，再次是7、8、2。诱导矩阵是固定的，可以根据经验来设定，比如风机4，按照经验可能的连接为2，3，5，7，8，而其中最可能连接的顺序为3，5，7，8，2。则诱导矩阵的第4行就为（3，5，7，8，2）。诱导矩阵的作用在于用人的经验去影响变异，加快求解的速度。本次的诱导矩阵取值是靠风机间的距离得出的，风机离得越近，诱导的概率越大。

变异操作：按一定概率选取粒子，随机选取粒子的解的某一位A，有概率的参考诱导矩阵，将该位的下一位C间插入另一值B，然后修复解，将另外一个B的位置删除，则得到变异的解。计算变异后的适应值，如果比变异前的更优，则替换。

2.2 基于粒子群的混合遗传算法主要步骤

本文在Matlab中编程实现基于粒子群的混合遗传算法，步骤如下[13，14]：Step1，初始化粒子群m，随机生成m个1到33+M-1的排列，计算每个粒子的个体极值Pi，并初始化为Xi，将全局极值g初始化为所有粒子中适应值评价最好的Xi。生成诱导矩阵K；Step2，每个粒子同它的粒子历史最优进行杂交，如果杂交结果的适应值优于粒子的当前适应值，则将粒子替换为杂交后的更优结果。对每个粒子，有一定概率对它进行变异，变异概率参照诱导矩阵，如果变异结果的适应值优于粒子的适应值，则将粒子替换为杂交后的更优结果；Step3，更新个体极值Pi：对每个粒子，将其适应值和个体极值Pi比较，如果优于Pi，则替换Pi；Step4，更新全局极值g：对每个粒子，将其适应值与全局极值比较g，如果优于g，则替换g；Step6，检查终止条件，若满足条件，则终止迭代，否则返回Step2。

3 实例分析

3.1 基本参数

拟建风电场一期装机容量为49.5MW，安装33台风力发电机组，单机容量为1500kW，风电机组接线方式采用一机一变单元接线方式。各个风机机位坐标见表2。

升压站坐标为：644000，4829000。

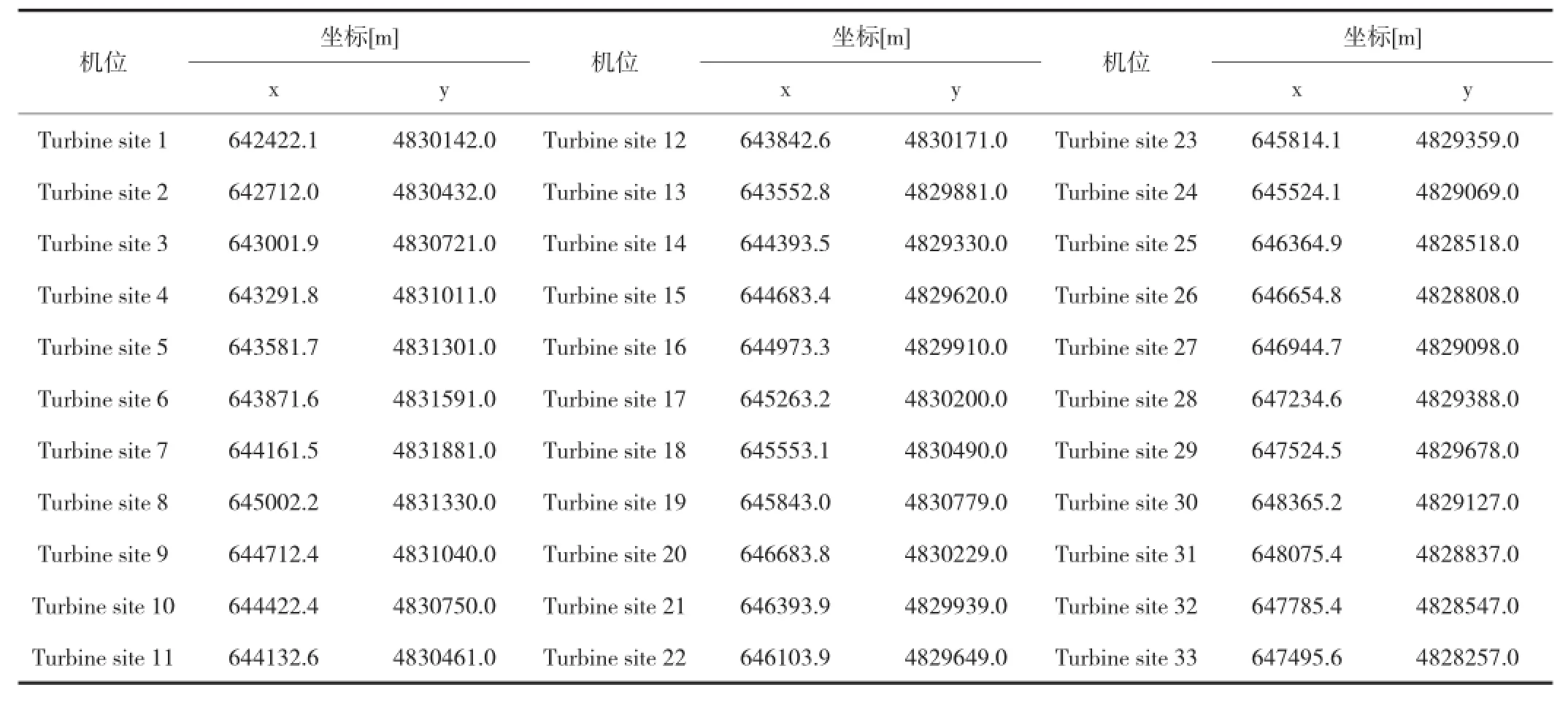
表2 机位坐标

其他参数设置见表3。

表3 其他参数设置表

3.2 运算结果

首先选取粒子群规模为50，迭代次数为100，取回路数为1-33进行循环，发现比较优的结果处于6-9回路之间。然后选取粒子群规模为500，迭代次数为1000，回路数为6-9，进行迭代，并且运行3次，观察迭代结果，发现7回路数总为最优。

选取粒子群规模为500，迭代次数为2000，回路数为7。运行程序10次。结果见表4。

观察结果，发现其中最优解为289362.0210元。运行10次共得到3次。最优解如图1所示。

最优解为（1，2，3，34，13，4，5，6，7，35，12，11，10，9，8，36，15，16，17，18，19，37，14，23，22，21，20，38，24，26，27，28，29，39，25，33，32，31，30）

方案为：

0-1-2-3；0-13-4-5-6-7；0-12-11-10-9-8；0-15 -16-17-18-19；0-14-23-22-21-20；0-24-26-27-28-29；0-25-33-32-31-30

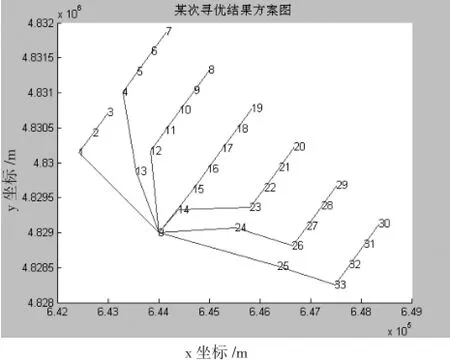
图1 某次寻优结果方案图

程序实现的收敛图如图2所示。

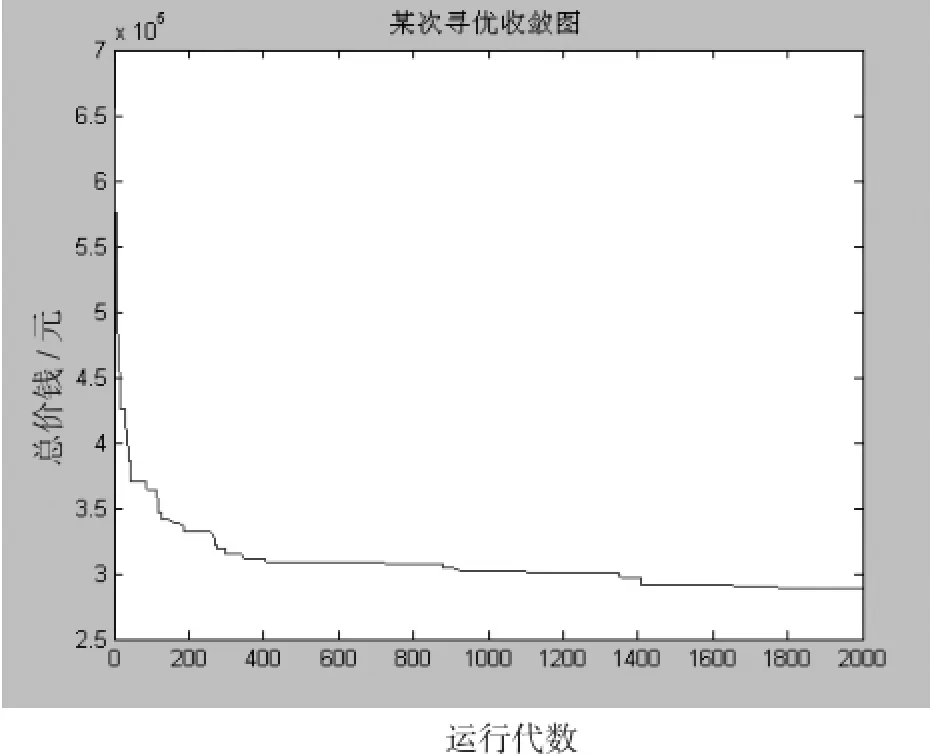
图2 某次寻优收敛图

从图2中可以看出，当迭代次数大于1600时，总价已趋于收敛，程序实现了总价精度达到30万元以内，可满足项目的工程造价需求。

4 结语

本文研究并实现了运用改进的PSO算法对风电场集电线路路径的优化。详细的分析了路径优化的过程实现及可以采用的方法，由于风电场集电线路路径优化问题，是一种类NP问题，并非多项式可表达问题，而是非线性的、离散的、多峰值问题。本文采用粒子群算法是由于其具有算法简单、计算速度快及收敛性较好的特点，但是传统的PSO算法还不能满足设计的要求，因为对于多峰值问题，PSO很容易陷入局部最优，很难求出最优或者近似最优解。因此本文对基本PSO做了进一步的改进，尽可能提高其收敛性能。在实现过程中借助遗传算法的选择，交叉及变异等较好方法达到了优化的要求。

[1]王锡凡.电力系统优化规划[M].北京：水利电力出版社，1990.

[2]苏志扬.浅谈电源规划与电网规划[J].电力建设，2004，25（8）.

[3]胡建秀，曾建潮.具有随机惯性权重的PSO算法[J].计算机仿真，2006，23（8）.

[4]王俊伟，汪定伟.粒子群算法中惯性权重的实验与分析[J].系统工程学报，2005，20（2）.

[5]王治国，刘吉臻.基于改进PSO算法的快速性厂级负荷优化分配研究[J].华北电力大学学报，2006，33（5）.

[6]任苹，李楠.集成粒子群优化算法在电网规划中的应用[J].系统仿真学报，2007，19（10）.

[7]袁晓辉，王乘.粒子群优化算法在电力系统中的应用[J].电网技术，2004，28（19）.

[8]孟懿，孟强，郭福娜.关于电网规划研究方法的探讨[J].黑龙江电力，2007，29（2）.

[9]Sensarma P.S，Rahmani M.A Comprehensive Method for Optimal Expansion Planning Using Particle Swarm Optimization[A].Proceedings of the IEEE Power Engineering Society Transmission and Distribution Coherence [C].New York（USA）：2002.1317～1322.

[10]肖燕，奚杰，阳薇.遗传算法在电网规划中的研究与应用[J].华北电力技术，2004，（6）.

[11]Da Silva E.L，Gil H A，Areiza J.M.Transmission network expansion planning under an improved genetic algorithm[A].IEEE Transactions on Power Systems[C].2000，15（8）：1168～1174.

[12]Sensarma P.S，Rahmani M，Carvalho A.A comprehensive method for optimal expansion planning using particle swarm optimization[A].Power Engineering Society Winter Meeting[C].27-31 Jan 2002，IEEE 2002，（2）：317～1322.

[13]Boeringer D.W，Werner D.H.A comparison of particle swarm optimization and genetic algorithms for a phased array synthesis problem[A].Antennas and Propagation Society International Symposium[C].22～27 June 2003，IEEE 2003（1）：181～184.

[14]Y.H.Shi，R.C.Eberhart.A modified particle swarm optimizer[A].in：Proc.of the IEEE Congress on Evolutionary Computation[C].USA：IEEE Service Center，1998.69～73.

Wind Farm Electric Transmission Line Optimization Based on Hybrid Genetic Algorithm and PSO Algorithm

LIU Jun1，LIU Qing-chao2，WEI Chao2
（1.Huadian Xinjiang Power Co.，Ltd，Urumqi 830063，China；2.Huadian Electric Power Research Institute，Hangzhou 310030，China）

As collecting power lines of wind farm has a direct impact on project cost，so how to choose reasonable path is crucial to the cost control and effectiveness improvement of wind farm.This paper proposed a thought about the minimum cost in the whole life-cycle running of collecting power lines，though establishing models below：line investment discounted function model，lines with different sections and length cost model，line length and loss cost model and line circuits and cost model，to realize the collecting circuit path optimization，provide the best path program to investors and designers.

Particle Swarm Optimization；current collection line；path optimization；genetic algorithm

10.3969/J.ISSN.2095-3429.2015.01.008

TM614

A

2095-3429（2015）01-0034-05

2014-09-02

修回日期：2014-12-05

刘军（1972-），男，湖北武汉人，本科,经济师,工程师，主要从事电力工程项目管理和造价控制工作。