密排六方金属{10 2}形变孪晶 长大机制的研究进展

涂 坚 ，周志明 ，柴林江 ，黄 灿

(1. 重庆理工大学 材料科学与工程学院，重庆 400054； 2. 重庆理工大学 重庆市高校模具技术重点实验室，重庆 400054)

镁合金具有质轻、导电性好和阻尼减振等优异性能，在交通、通讯和航空航天等领域有广阔的应用前景。发展高性能镁合金材料、提高镁合金的制备加工水平对于实现从镁资源优势向经济优势的转化具有重要意义。但由于镁合金具有密排六方(Hexagonal close packed, HCP)晶体结构的特点，在室温变形条件下独 立的滑移系少，导致室温塑性低以及变形加工困难，已成为阻碍镁合金材料大规模应用的瓶颈问题[1]。细化晶粒可作为提高镁合金力学性能与塑性加工能力的有效途径。目前，针对镁合金细化晶粒的方法主要有合金化、粉末冶金、快速凝固、剧烈塑性变形等[2-8]。但是，合金化中昂贵的稀土元素增加了材料的成本；粉末冶金和快速凝固等方法不可避免地会引入杂质或缺陷，且工艺复杂；剧烈塑性变形需要特殊的加工设备并消耗大量热能。因此，如何利用简单易行和低成本的方法细化镁合金晶粒，改善镁合金的室温塑性和加工性能将对推进镁合金材料大规模应用至关重要。

最新研究表明，预置{1 012}孪晶可作为开发低加工成本及高性能镁合金的有效途径[9-11]。预置{1012}孪晶调整镁合金组织和性能具有3 个优势：1) 孪晶分割晶粒，细化基体组织，提高镁合金综合性能；2) 孪晶改变晶粒晶体取向，弱化基面织构，改善镁合金塑性变形能力；3) 室温下沿特定方向的预变形可轻易的引入大量的{1 012}孪晶。因此，深入、系统地理解{1 012}孪生变形的微观物理本质，是利用{1 012}孪生变形调整镁合金组织和性能的关键。

迄今为止，国内外学者应用孪生晶体学理论[12]、分子动力学计算机模拟[13-27]和高分辨透射电镜[28-40]等研究手段，对{1 012}孪生的变形机制开展了一系列的研究工作。但对{1 012}孪晶长大机制存在很大的争 议[1,41-43]，主要争议在于如何解释{1 012}孪晶界大角度偏离{1 012}孪晶面。孪晶界面精细结构调控孪晶界的迁移扩展形式，因此，考察孪晶界面精细结构则显得至关重要[12]。对此，本文作者从{1 012}变形孪晶界面形态及其精细结构着手，对{1 012}孪晶长大机制进行综合评述。

1 {10 12}孪晶界面精细结构

经典孪生晶体学理论表明，孪生后晶体的切变部分与未变形部分以孪生面保持镜面对称的位相关系，因此，{1 012}孪晶界面应严格地处于{1 012}孪生面(K1面)。这一晶体学理论上的定义在实验上得以验证(见图1)。图1(a)所示为 Mg-Zn 合金的{1 012}孪晶界的大倾角环形暗场扫描透射电子显微镜(HAADF-STEM)像[44]，图1(b)所示为Co 金属{1012}孪晶界的高分辨透射电镜(HRTEM)[29]，图1(c)所示为单晶镁{1 012}孪晶界的HRTEM 像[45]。图1 表明{1 012}孪晶界为连续性的完全共格界面(Coherent twinning boundary, CTB)，即{1 012}孪晶界位于{1 012}孪晶面。在{1 012}孪晶界面迁移扩展过程中，{1 012}孪晶面可作为分离基体和孪晶的一个对称 界面。

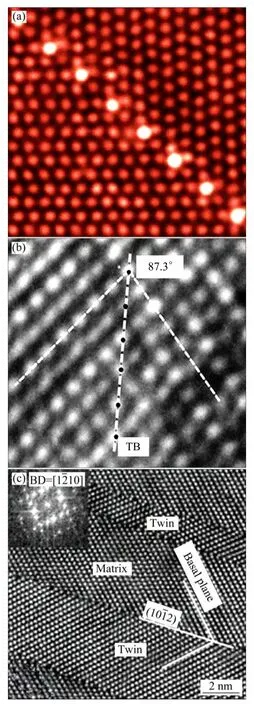
图1 {1 012}孪晶界面精细结构 Fig. 1 Microstructures of {1 012} twins in alloys[44] (a) AZ31 Mg alloy; (b) Co[29]; (c) Single crystal magnesium[45]

{1 012}孪晶宏观形貌为凸透镜状，允许{1 012}孪晶界偏离{1 012}孪晶面，但偏离通常为小角度偏离。这种小角度偏离被众多研究者认为是滑移应变的容纳，滑移位错与孪晶间的相互作用，以及孪晶和孪晶间的相互作用等的结果，从而破坏了完全共格孪晶界面(CTB)，最终以界面缺陷的形式存在于孪晶界 上[18-19,32-33,46]。图2 所示为金属Zn[31]、Co[29]和Ti[33]的{1 012}孪晶界中界面缺陷的HRTEM 像，图2 中界面缺陷表现为共格型孪晶界面存在断开的部分，呈现界面不连续的特征。

图2 {1 012}孪晶不同类型界面缺陷的HRTEM 像 Fig. 2 HRTEM images of different kinds of interface defect existing in {1 012} twinning boundary in Zn (a) [31], Co (b) [29] and Ti (c) [33]

图3 Co 和镁合金AZ31 的{1 012}孪晶TEM 明场像 Fig. 3 Bright field TEM images of deformation twins in Co (a) and AZ31 Mg alloys (b) (Apparently trace of {1 012} twinning plane does not match actual twin boundary[30])

最近实验结果显示：{1 012}孪晶界并不在{1012}孪晶面上(存在大角度的偏离)，表明{1 012}孪生所需的不变平面这一规则在{1 012}孪生中是不成立 的[15,30,47-49]。图3 所示为Co 和AZ31 的{1 012}孪晶 TEM 明场像[30]，基面(0001)和{1 012}面用绿虚线表示。由图3 可知，{1 012}孪晶界并不在{1 012}孪晶面，{1 012}孪晶界大角度偏离{1 012}孪晶面。{1 012}孪晶界偏离孪生面的现象在HRTEM下也得到证实(见图4)。图4(a)所示[30]为 Co 的{1 012}孪晶高分辨像，表明在原子尺度下{1 012}孪晶界的确不位于{1 012}孪晶面；图4(b)所示为AZ31 的{1 012}孪晶高分辨像[47]，表明即使{1 012}界面(绿虚线)为连续性共格孪晶界界面(CTB)，但基体中的{1 012}面(红实线)和孪晶中的{1 012}面(黄实线)仍然不重合，即{1 012}孪晶界不位于{1 012}孪晶面。

图4 Co 和镁合金AZ31{1 012}孪晶界的HRTEM 像 Fig. 4 HRTEM images of {1 012} twin boundaries in Co and AZ31 Mg alloys: (a) {1 012} TB in Co[30]; (b) {1 012} TB in AZ31[47]

以上为国内外学者利用透射电镜对{1 012}孪晶界精细结构的表征研究结果，其中有研究结果表明在{1 012}孪生变形过程中，{1 012}孪晶面可作为分离基体和孪晶的一个对称界面，为完全共格界面(见图1)，且孪晶界小角度偏离孪晶面可用界面缺陷弥补(见图2)；但有实验结果表明{1 012}孪晶界并不在{1 012}孪晶面(存在大角度的偏离)(见图3 和4)。经典孪生晶体学表明，在共格型的{1 012}孪晶界面上存在一种孪生位错(该位错的剪切方向严格平行于孪生方向〈1 0 11〉)，因此，该位错在剪切应力作用下使得孪晶界扩展，最终导致孪晶长大[12]。但是，非共格{1 012}孪晶界面已经完全偏离了{1 012}孪晶面的孪生方向，那么这种孪晶界面的长大方式能否由孪生位错来控制有待于进一步研究。

2 {10 12}孪晶长大机制

2.1 滑动型界面机制

滑动型界面机制是指界面的移动是靠位错的滑动而迁移的，其结果使基体点阵切变而转化为生长 相[12]。经典的孪生晶体学理论表明孪晶的生长，是以孪生位错的运动来完成的(属于滑动界面机制)。针对于{1 012}孪晶生长，为孪生位错在{1 012}孪晶面上做相对迁移的结果(见图5)[12]。{1 012}孪生位错在图5中标记为“⊥”，且对孪生位错更为具体的描述见文献[12]。若相继的原子面上各扫过一个孪生位错，即造成均匀切变的孪晶，可满足形成共格的{1 012}孪晶 界面。

图5 孪生位错示意图[12] Fig. 5 Schematic diagram of twinning dislocation[12]

图6 Co[29]和Zn[31]中{1 012}孪生位错的高分辨像和计算机模拟{1 012}孪生位错[42] Fig. 6 HRTEM images of {1 012} twinning dislocation in Co (a)[29] and Zn (b)[31] and atomic computer simulation (c)[42]

图6(a)[29]和(b)[31]所示分别为金属Co 和金属Zn中{1 012}孪生位错的HRTEM 像。由图6(a)可知，Co中{1 012}孪晶的孪生位错核心结构紧凑，孪生位错的柏氏矢量大小为0.154a(由构造柏氏回路计算得出)，其台阶高度(h)为两倍的{1 012}晶面间距。由图6(b)可知，Zn 中{1 012}孪生位错的核心结构也很紧凑， 与Co 中的{1 012}孪生位错结构类似。{1 012}孪生位错也存在于计算机模拟中(见图6(c))[42]，SERRA 等[42]围绕着这个“台阶”构造柏氏回路，证实这个台阶为{1 012}孪晶的孪生位错。{1 012}孪生位错在分子动力学计算机进行模拟，结果表明该位错的能量和其移动能力与其核心宽度有关，且模拟结果表明{1 012}孪生位错核心结构宽大[20-21]。尽管目前国内外学者对孪生位错核心宽度的认识上存在争议(实验和模拟结果不符合)，但以上的研究结果表明{1 012}孪生位错的确存在于{1 012}孪晶中。

BILBY 等[50]基于孪生晶体学理论，构造了基体原子经孪生位错的剪切和曳步组合运动后而转变为孪晶(见图7)。在{1 012}孪生过程中，孪生位错内部原子的具体过程包括：剪切运动(Shear，运动方向平行于孪生方向〈1 0 11〉，见图 7 中Ⅰ步骤)和曳步运动(Shuffle，运动方向不平行于孪生方向〈1 0 11〉，见图7中Ⅱ步骤)的组合运动，从而使得基体中的原子转变为孪晶的原子，形成{1 012}孪晶，从而满足基体与孪晶之间的镜面对称关系。因此，一旦孪生位错形成，则可通过{1 012}孪生位错的剪切和曳步组合运动，使得基体中的原子转变为孪晶的原子。国内外学者的研究表明，形成孪生位错的机制包括极轴机制[51]、界面缺陷机制[52]等。这两种生成孪生位错的机制将分别被介绍。

极轴机制为当一个〈c〉型位错(b=[0001])插入在孪晶界的两个点，随后它分解成一对孪生位错[51]。这种分解方式如同弗兰克位错源，孪生位错使孪晶沿垂直于孪生面 K1的方向增厚。但是，问题在于{1 012}孪晶的长大速度非常快，所以孪生位错需要在很短的时间里大量地形成，且孪生位错必须是高速移动的。遗憾的是，现在没有任何实验证据能够表明极轴机制可以满足孪晶的长大所需条件。

图7 基体原子经孪生位错的剪切和曳步组合运动后转变为孪晶的示意图[50] Fig. 7 Schematic diagram of atomic movement combined with Shearing and Shuffling in {1 012} twin[50]

另一种形成孪生位错的机制为界面缺陷机制 (见图8[52])。该机制的基本思想为，当一个螺型位错b=1 /3〈1 120〉穿过{1 012}孪晶界时与孪晶界发生相互作用，反应式为b1/10→b-(2n-1)/-2n+nb2/2，最后残余位错在高应力集中的作用下可作为孪生位错的发射源。对于金属Ti，分子动力学计算机模拟表明[52]，在反应式b1/10→b-(2n-1)/-2n+nb2/2中，当n=3 时，即b-5/-6为最稳定的压杆缺陷(见图8(a)和(b))。而当压杆缺陷存在一个应力集中时，一对孪生位错将会在压杆缺陷的台阶处的两端(A 和B)处形成(见图8(c))。在A 处的孪生位错标记为正刃型位错并且在剪切应力τ 下向左移动，在B 处的孪生位错为负刃型位错在剪切应力τ 下向右运动。此时，当一对孪生位错滑移并远离了界面缺陷，孪晶界则会以2d 的晶面间距高度向下迁移(见图8(d))。而另外一对孪生位错可以形核并且在孪生剪切应力的作用下重复以上的运动，从而使得孪晶不断地以2d 的间距增厚，最终导致孪晶长大。从以上分析得到，一个稳定的界面缺陷(压杆位错)可以作为孪生位错形成的核心，在这个缺陷处会有源源不断的孪生位错被发射出来(其过程类似于弗兰克位错源)。但是，目前尚未有实验证据表明存在这一类的压杆缺陷来作为孪生位错源，仅仅只是在计算机模拟上得到证实。

2.2 非滑动型界面机制

最近的高分辨实验结果(见图3 和4)表明，{1012}孪晶界可以完全偏离{1 012}孪晶面[30,40,47-49]。有学者认为：这一实验现象不能通过经典的{1 012}孪生理论来解释，即{1 012}孪晶长大不能由一个均匀的剪切机制(孪生位错机制)所完成[41]。原因在于：1) {1012}晶面间距为0.19 nm，比(0001)基面间距(0.26 nm)要小的多；且{1 012}晶面的原子实际上是处于两个分开的面上(“褶皱”效应)，有效的晶面间距会更小；所以孪生位错在{1 012}面滑移是非常困难的；2) 孪生位错机制只能使得{1 012}孪晶界严格地平行于孪生方向，而与一些实验结果不符(见图3 和4)。对此，LI 等[41]提出的纯曳步(shuffle)机制(为非滑动性界面机制)来完成{1 012}孪生过程，曳步机制不需要通过孪生位错的剪切，而是通过原子晶胞的重构使得基体转变为孪晶 (见图9)。

图9 所示为{1 012}孪生曳步机制的过程[41]。图9(a)所示为一个密排的Mg 单胞晶格结构，…ABAB…代表不同的基面，用不同的颜色标记。图9(b)所示为沿着〈 01 10〉方向投影的Mg 单胞晶格，在这种二维的图像中好像“隐藏”着一个新的“基面”，正如在图9(b)中用{1 012}的实线连出来的那样。曳步机制可以实现基面和柱面之间的转换，也就是基体中的柱面在发生孪生变形时， 通过曳步的运动方式转变为孪晶中的基面。然而，如果只是按图9(b) 中所描述的那样，其结 果仅仅是晶格结构的重新构建，还是无法满足正确的密排六方结构，原子必须还要经过一些位置上的调整。再次，为了新形成的晶面方向也满足…ABAB…的堆垛关系(见图9(c))，要求第二层的原子(用蓝色标记的原子面还有深粉色的原子面)还必须向下移动1/6[0001]，约等于/6距离，到达在图9(c)中标出的原子位子(如M 移动到N)。最后，原子间还需要较小的曳步来调整轴比的关系，从而满足{1 012}孪晶 关系。

图8 缺陷b-(2n-l)/-2n 作为发射孪生位错(b2/2)源的示意图[52] Fig. 8 Schematic diagrams of role of b-(2n-l)/-2n defect for emitting twinning dislocations (b2/2)[52]: (a) Sessile disbocations existing in {1 012} twinning boundary; (b) b-(2n-1)/-2n defects consisting of b1/0 and nb-2/-2; (c) Nucleation of a pair of equal and opposite b2/2 twinning dislocations at A and B; (d) Twinning boundary and step moving toward by 2d

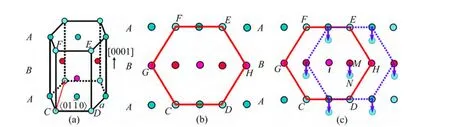
图9 {1 012}孪晶长大的曳步机制原子示意图[41] Fig. 9 Schematic diagrams of shuffling mechanism[41]: (a) 3D view of HCP Mg lattice (Colored basal planes showing normal stacking sequence ABAB…along 〈c〉 direction); (b) New basal plane constructed by connecting atoms with spacing in direction along 〈0 1 10〉; (c) Establishing correct HCP stacking sequence to shuffle by 1/6〈c〉 (0.09 nm)

密排六方晶格的重新构建实现了基面和柱面的转换，使得孪晶与基体成90°的取向关系。而当取向差不等于90°时，每个原子的曳步的幅度和方向可以稍微调整一下，使得对90°的偏离可以得到补偿[47]。由此可见，当曳步机制作为{1 012}孪晶形成长大机制时，可使{1 012}孪晶面偏离孪生面(K1面)。另外，研究表明：原子的曳步运动能够产生一个垂直于c 轴的应变，而不一定要涉及到孪生位错和孪生切变，且在孪生过程中产生的应变可以由基体和孪晶之间的不匹配应变所容纳[47]。

SERRA 等[46]对LI 等学者所提出的曳步机制进行了综合评述，认为LI 等[47]误解他们分子动力学计算机模拟结果，且指出{1 012}孪晶的长大是由孪生位错在孪晶界上的移动所完成的，而不是纯曳步机制。SERRA 等[46]认为，孪生位错在某种概念上来讲的是一个“完整”一部分，且孪晶界倾斜于K1面是由于界面缺陷的存在导致的(而不是由曳步机制导致的)。但是需要注意的是，在实验观察中(见图3 和4)，{1012}孪晶界已经完全不在{1 012}孪晶面上，所以不能简单地认为孪晶界倾斜K1面是由于界面缺陷的存在导致，原因在于即使孪晶界偏移孪晶面，那么在非缺陷处的孪晶界也要回到{1 012}面上(见图2)，不大可能完全偏离{1 012}面，所以仅仅用界面缺陷来解释孪晶界的大角度偏差是不完全合理的。而通过原子曳步机制可以轻微地调整来满足这些偏差而不引入任何均匀剪切，可以解释{1 012}孪晶界已完全不在{1 012}孪晶面上。

值得关注的是，最近本人作者笔者对钴中{1012}孪晶界精细结构进行细致表征，首次在实验上将{1 012}孪晶界面系统地表征为连续性界面(Coherent twinning boundary, CTB)和基面-柱面孪晶界面(Basal-prismatic interface, BP/PB)[28]。鉴于BP/PB 界面的提出，本文作者认为{1 012}孪晶界的迁移扩展形式不能由孪生位错简单的剪切滑移完成[28]。随后，针对BP/PB 界面的研究引起了计算机模拟工作者的极大兴趣，且研究结果表明：BP/PB 界面的存在可提高{1 012}孪晶界的迁移扩展能力[23-26,39-41,53]。但是，针对BP/PB 界面是如何调控{1 012}孪晶界大角度偏离孪生面(K1面)，以及BP/PB 界面是如何影响{1 012}孪晶界面迁移扩展是不清楚的。因此，仍需进一步对{1 012}孪晶界面精细结构进行表征，尤其是对BP/PB界面的表征。另外，借助分子动力学计算机模拟BP/PB界面的迁移形式，可进一步揭示的{1 012}孪生变形的物理本质。

3 结论与展望

1) 近年来，学者们结合孪生晶体学理论、分子动力学计算机模拟以及高分辨透射电镜对密排六方(HCP)金属的{1 012}孪晶界面精细结构进行了研究与表征，但依据不同理论和实验结果所提出来的{1012}孪生长大机制却存在很大的差异，导致对HCP 金属变形过程中孪晶长大过程认识不清，观点也不统一。对此，本文作者认为有必要对{1 012}孪生长大机制进一步深入研究。

2) 首先，孪晶界面性质决定孪晶界面的迁移形式，所以有待系统地利用高分辨透射电镜表征{1012}孪晶形态及其界面精细结构，和与孪晶界面密切相关的晶体缺陷的性质。其次，在实验表征结果的基础上，结合位错理论和孪生晶体学理论，以及借助分子动力学计算机模拟技术模拟{1 012}孪晶界面的迁移形式，从而进一步探讨和确定{1 012}孪生变形时其原子的移动规律，最终期待揭示{1 012}孪晶长大的物理本质。最后，值得研究人员注意的是，{1 012}孪晶长大是在{1 012}孪晶形核的基础上，所以研究{1 012}孪晶形核也具有重要的科学意义，这将有利于进一步探索{1 012}孪晶长大机制。

3) 然而，利用高分辨透射电镜只能观察到已经长大了的孪晶。对此，本文作者认为利用分子动力学再结合位错理论等可作为研究孪晶形核的一个重要科研手段，模拟{1 012}孪晶的长大过程。总之，对HCP金属{1 012}孪生变形机制的探索，无论是对物理冶金基础科学问题认识的丰富和发展，还是对HCP 金属塑性加工关键技术的发展都具有非常重要的理论意义与实际意义。

[1] 余 琨, 黎文献, 王日初. 镁合金塑性变形机制[J]. 中国有色金属学报, 2005, 15(7): 1081-1086. YU Kun, LI Wen-xian, WANG Ri-chu. Plastic deformation mechanism for magnesium alloy[J]. The Chinese Journal of Nonferrous Metals, 2005, 15(7): 1081-1086.

[2] HU Hong-jun, ZHANG Ding-fei, YANG Ming-bo, DENG Ming. Grain refinement in AZ31 magnesium alloy rod fabricated by extrusion-shearing severe plastic deformation process[J]. Transactions of Nonferrous Metals Society of China, 2011, 21(2): 243-249.

[3] XU Yan, HU Lian-xi, YU Sun, JIA Jian-bo, JIANG Ju-fu. Microstructure and mechanical properties of AZ61 magnesium alloy prepared by repetitive upsetting-extrusion[J]. Transactions of Nonferrous Metals Society of China, 2015, 25(2): 381-388.

[4] XIA Xiang-sheng, CHEN Ming, FAN Fu-you, ZHU Chun-hua, HUANG Jing, DENG Tian-quan, ZHU Si-feng. Microstructure and mechanical properties of isothermal multi-axial forging formed AZ61 Mg alloy[J]. Transactions of Nonferrous Metals Society of China, 2013, 23(11): 3186-3192.

[5] 杨 伟, 陈寿辉, 张守银, 余 欢, 严青松, 蔡长春. 冷却速率对AZ91D镁合金非平衡凝固组织的影响[J]. 中国有色金属学报, 2014, 24(3): 593-599. YANG Wei, CHEN Shou-hui, ZHANG Shou-yin, YU Huan, YAN Qing-song, CAI Chang-chun. Effect of cooling rate on non-equilibrium solidified microstructure of AZ91D magnesium alloy[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(3): 593-599.

[6] YAMASHITA A, HORITA Z, LANGDON T. Improving the mechanical properties of magnesium and a magnesium alloy through severe plastic deformation[J]. Materials Science and Engineering A, 2001, 300: 142-147.

[7] STJOHN D, EASTON M, QIAN M, TAYLOR J. Grain refinement of magnesium alloys: A review of recent research, theoretical developments, and their application[J]. Metallurgical and Materials Transactions A, 2013, 44: 2935-2949.

[8] 李玉娟, 汤爱涛. 镁合金晶粒细化的研究进展[J]. 材料导报, 2013. 27: 125-130. LI Yu-juan, TANG Ai-tao. Recent development of grain refining technologies for magnesium alloys[J]. Materials Review, 2013. 27: 125-130.

[9] XIN Y, ZHOU X, LÜ L, LIU Q. The influence of a secondary twin on the detwinning deformation of a primary twin in Mg-3Al-1Zn alloy[J]. Materials Science and Engineering A, 2014, 606: 81-91.

[10] SONG B, GUO N, LIU T T, YANG Q S. Improvement of formability and mechanical properties of magnesium alloys via pre-twinning: A review[J]. Materials & Design, 2014, 62: 352-360.

[11] XIN Y, WANG M, ZENG Z, NIE M, LIU Q. Strengthening and toughening of magnesium alloy by {1 012} extension twins[J]. Scripta Materialia, 2012, 66: 25-28.

[12] CHRISTIAN J W, MAHAJAN S. Deformation twinning[J]. Progress in Materials Science, 1995, 39: 1-157.

[13] YUASA M, HAYASHI M, MABUCHI M, CHINO Y. Atomic simulations of (1012),(1 011) twinning and (1 012) detwinning in magnesium[J]. Journal of Physics: Condensed Matter, 2014, 26: 015003.

[14] XU B, CAPOLUNGO L, RODNEY D. On the importance of prismatic/basal interfaces in the growth of {1 012} twins in hexagonal close packed crystals[J]. Scripta Materialia, 2013, 68: 901-904.

[15] LIU B, LI B, SHAN Z. Twin boundary migration creating zero shear strain: In-situ TEM observations and atomistic simulations[J]. Magnesium Technology, 2013: 107-111.

[16] MORRIS J R, YE Y, YOO M H. First-principles examination of the twin boundary in HCP metals[J]. Philosophical Magazine, 2005, 85: 233-238.

[17] BÉRÉ A, BRAISAZ T, RUTERANA P, NOUET G. Twinning and extended defects in HCP metals with large c/a ratio: Modelling and microscopic observations[J]. Physica Status Solidi, 2005, 202: 2900-2911.

[18] SERRA A, BACON D J, POND R C. Dislocations in interfaces in the HCP metals—Ⅰ. Defects formed by absorption of crystal dislocations[J]. Acta Materialia, 1999, 47: 1425-1439.

[19] POND R C, SERRA A, BACON D J. Dislocations in interfaces in the HCP metals—Ⅱ. Mechanisms of defect mobility under stress[J]. Acta Materialia, 1999, 47: 1441-1453.

[20] SERRA A, POND R C, BACON D J. Computer simulation of the structure and mobility of twinning disclocations in HCP metals[J]. Acta Materialia, 1991, 39: 1469-1480.

[21] SERRA A, BACON D J. Computer simulation of twinning dislocation in magnesium using a many-body potential[J]. Philosophical Magazine, 1991, 63: 1001-1012.

[22] SERRA A, BACON D J. Computer simulation of twin boundaries in the HCP metals[J]. Philosophical Magazine, 1986, 54: 793-804.

[23] WANG J, LIU L, TOME C, MAO S, GONG S. Twinning and de-twinning via glide and climb of twinning dislocations along serrated coherent twin boundaries in hexagonal-close-packed metals[J]. Materials Research Letters, 2013, 1: 81-88.

[24] OSTAPOVETS A, SERRA A. Characterization of the matrix– twin interface of a twin during growth [J]. Philosophical Magazine, 2014, 94: 2827-2839.

[25] BARRETT C D, El KADIRI H. The roles of grain boundary dislocations and disclinations in the nucleation of {1 012} twinning[J]. Acta Materialia, 2014, 63: 1-15.

[26] KADIRI H, BARRETT C D, WANG J, TOMÉ C N. Why are twins profuse in magnesium[J]. Acta Materialia, 2015, 85: 354-361.

[27] GUO Y, WANG Y, QI H, STEGLICH D. Atomistic simulation of tension deformation behavior in magnesium single crystal[J]. Acta Metallurgica Sinica, 2010, 23: 370-380.

[28] TU J, ZHANG X Y, WANG J, SUN Q, LIU Q, TOME C N. Structural characterization of {1 012} twin boundaries in cobalt [J]. Applied Physics Letters, 2013, 103: 051903-1-4.

[29] TU J, ZHANG X Y, LOU C, LIU Q. HRTEM investigation of {1 012} twin boundary and interface defects in deformed polycrystalline cobalt [J]. Philosophical Magazine Letters, 2013, 93: 292-298.

[30] ZHANG X Y, LI B, WU X L, ZHU Y T, MA Q, LIU Q, WANG P T, HORSTEMEYER M F. Twin boundaries showing very large deviations from the twinning plane[J]. Scripta Materialia, 2012, 67(10): 862-865.

[31] BRAISAZ T, RUTERANA P, NOUET G, POND R C. Investigation of {1 012} twins in Zn using high-resolution electron microscopy: Interfacial defects and interactions[J]. Philosophical Magazine, 1997, 75(4): 1075-1095.

[32] BRAISAZ T, RUTERANA P, NOUET G. Twin tip defects related to the nucleation and growth mechanisms of the twin (1 012) in zinc characterized by high-resolution electron microscopy[J]. Philosophical Magazine, 1997, 76(1): 63-84.

[33] BRAISAZ T, RUTERANA P, NOUET G. High-resolution electron microscopy study of the (1 012) twin and defects analysis in deformed polycrystalline alpha titanium[J]. Philosophical Magazine Letters, 1996, 74(5): 331-338.

[34] LAY S, NOUET G. Morphology of (0 112) twins in zinc and related interfacial defects[J]. Philosophical Magazine, 1995, 72: 603-617.

[35] LAY S, NOUET G. Interaction of slip dislocations with the (0 112) twin interface in zinc[J]. Philosophical Magazine, 1994, 70: 1027-1044.

[36] LAY S, NOUET G. HRTEM study of the (0 112) twin interface in zinc[J]. Philosophical Magazine, 1994, 70: 261-275.

[37] LAY S, AYED P, NOUET G. A study of (0 112) twin deviating from exact orientation in magnesium[J]. Acta Materialia, 1992, 40: 2351-2359.

[38] SUN Q, ZHANG X, TU J, REN Y, QIN H, LIU Q. Characterization of basal-prismatic interface of twin in deformed titanium by high-resolution transmission electron microscopy[J]. Philosophical Magazine Letters, 2015, 95: 145-151.

[39] SUN Q, ZHANG X, TU J, REN Y, QIN H, LIU Q. Interfacial structure of {1 012} twin tip in deformed magnesium alloy [J]. Scripta Materialia, 2014, 90: 41-44.

[40] LIU B, WAN L, WANG J, MA E, SHAN Z. Terrace-like morphology of the boundary created through basal-prismatic transformation in magnesium[J]. Scripta Materialia, 2015, 100: 86-89.

[41] LI B, MA E. Atomic shuffling dominated mechanism for deformation twinning in magnesium[J]. Physical Review Letters, 2009, 103: 033503-1-4.

[42] SERRA A, BACON D J, POND R C. Comment on atomic shuffling dominated mechanism for deformation twinning in magnesium[J]. Physical Review Letters, 2010, 104: 029603.

[43] LI B, MA E. LI and Ma reply[J]. Physical Review Letters, 2010, 104: 029604.

[44] NIE J, ZHU Y M, LIU J Z, FANG. X Y. Periodic segregation of solute atoms in fully coherent twin boundaries [J]. Science, 2013,340: 957-960.

[45] YU Q, QI L, CHEN K, MISHRA R K, LI J, MINOR A M. The nanostructured origin of deformation twinning[J]. Nano Letters, 2012, 12: 887-892.

[46] SERRA A, BACON D J. Interaction of a moving {1 012} twin boundary with perfect dislocations and loops in a HCP metal[J]. Philosophical Magazine, 2010, 90: 845-861.

[47] LI B, ZHANG X. Strain generated by shuffling-dominated twinning[J]. Scripta Materialia, 2014, 71: 45-48.

[48] LIU B Y, WANG J, LI B, LU L, ZHANG X Y, SHAN Z W, LI J, JIA C L, SUN J, MA E. Twinning-like lattice reorientation without a crystallographic twinning plane[J]. Nature Communications, 2014, 5: 3297.

[49] ZHANG X, LI B, TU J, SUN Q, LIU Q. Non-classical twinning behavior in dynamically deformed cobalt[J]. Materials Research Letters, 2015, 3: 142-148.

[50] BILBY B A, CROCKER A G. The theory of the crystallography of deformation twinning[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1965, 288: 240-255.

[51] THOMPSONA N, MILLARDA D J. Twin formation, in cadmium[J]. Philosophical Magazine, 1952, 43: 422-440.

[52] SERRA A, BACON D J. A new model for {1 012} twin growth in HCP metals[J]. Philosophical Magazine, 1996, 73: 333-343.

[53] BARRETT C, KADIRI H. Impact of deformation faceting on and embryonic twin nucleation in hexagonal close-packed metals[J]. Acta Materialia, 2014, 70: 137-161.