步进电动机细分精度自动补偿的研究

罗东辉

(中国电子科技集团公司第二十一研究所，上海200233)

0 引 言

步进电动机作为开环位置和速度伺服驱动元件，具有使用方便、可靠性高等优点，目前在很多运动控制场合依然采用了步进电动机伺服驱动方式。但由于步进电动机的固有特性，因此在应用中通常存在以下两个问题:

(1)由于步进电动机的力矩脉动较大，因此在运行过程中尤其是在低频运行时存在着较大的振动和噪声;

(2)由于步进电动机的加工原因，一般步进电动机的步距角都比较大，二相混合式步进电动机的整步步距角一般为0.9°和1.8°，因此在一些场合满足不了定位分辨率的要求。

为了解决上述这两个问题，在步进电动机驱动方式上大多采用了细分驱动(国外称为微步驱动microstep drive)的方法，细分驱动是一种增加电机运行平稳性、提高定位分辨率的有效方法。

本文通过对二相混合式步进电动机在细分运行时的步距均匀性的分析，给出了对步矩角细分精度的自动补偿方法，从86BH001 型二相混合式步进电动机进行自动补偿前后的数据对比可以看出，经过自动补偿后步进电动机的细分步矩角精度得到了很大提高。

1 步进电动机细分精度分析及补偿方法

二相混合式步进电动机的简单模型如图1 所示，当步进电动机单相通电时，其稳态转矩:

式中:θ 为电机转子偏离参考点的角度，i 为绕组中通过的电流。假设:

(1)电机磁路为线性，即T =k1i;k1为力矩系数。

(2)矩角特性为正弦型，即T=TMsinθ;TM为最大转矩;θ 为电机转子偏离参考点的角度。

图1 二相混合式步进电动机的简单模型

这时当电机二相绕组通以正交的正弦波电流，即:

Im为步进电动机绕组的最大电流时，电机的稳态转矩可表达成:

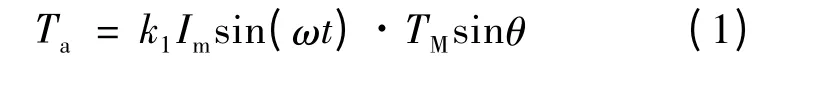
根据电机的向量时空图，如图2 所示，式(1)、式(2)可写成:

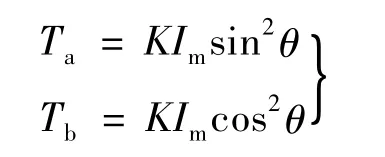
式中:K=k1TM。

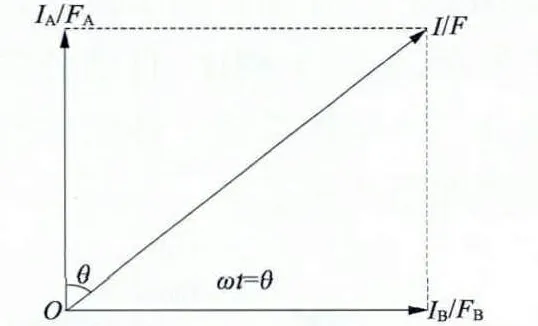
图2 向量时空图

因此电机的合成输出转矩T = Ta+ Tb= KIm。可见，当二相绕组通以正交的正弦电流时，对于理想的二相混合式步进电动机，其输出转矩为恒定值，如果将正弦电流等分量化后(量化后的正弦波称之为拟正弦波)，则能够得到均匀的细分步距角。

但是，对于通常的二相混合式步进电动机，由于电机的矩角特性并非为理想的正弦型和电机磁路的饱和造成的电机磁路非线性，因此当二相绕组通以正交拟正弦电流时，细分步距角的精度将会变差。实测86BH001 型二相混合式步进电动机当二相绕组通以16 细分量化的正交拟正弦波电流时的细分步矩角与细分步数之间的关系如图2 所示，与理论值相比，其最大误差达0.216 5°，而理想的细分步距角为0.112 5°。

由此可见，当直接通以拟正弦波电流时细分步矩角误差相当大。如果想得到均匀的细分步距角就必须对图3 中的曲线进行补偿。

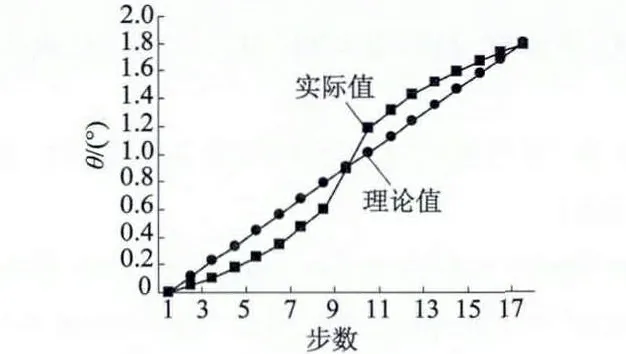
图3 二相步进电动机细分角度测试曲线

对步进电动机细分电路进行电流补偿，一般采用先在步距角测量仪上测出二相绕组通以细分量化的正交电流时的细分步距角与步进电动机的转子机械位置角之间的关系，再利用插值的方法对其误差进行补偿。插值的方法有很多种，如诺顿插值、线性插值等等。实验表明，在对步进电动机细分步距的数据进行插值时，采用线性插值即可得到满意的结果。

设θ 为步进电动机的整步步距角，N 为细分数。对于N 细分时每一细分步的拟正余弦电流值可表示:

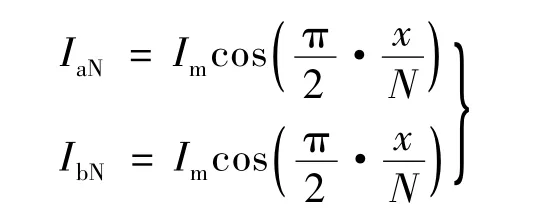
式中:x=1，2，…，N;Im为步进电动机绕组的最大电流。

通过试验而测得的一组实际细分步距角为θ'

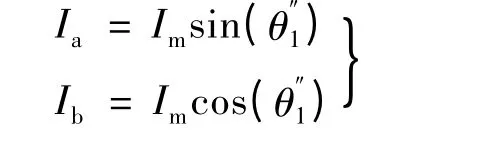
2 细分电路电流补偿的实际实现

由以上讨论可见，要实现步进电动机的细分，必须在步进电动机的二相绕组中通以补偿后的拟正弦波电流。目前，国内外有很多集成电路生产厂家均推出了系列的步进电动机细分专用驱动芯片，如海华博远、TI、ALLEGRO、ONSEMI、TOSHIBA 等公司均提供集成的此类芯片。这类芯片外围电路简单、工作稳定可靠，但是都存在一个共同的缺陷:它们都通过采用在电机绕组中通以拟正余弦电流来实现细分驱动，对于专为细分运行设计的步进电动机来讲，这种电流波形在驱动时能得到较高的细分精度，但是，当驱动通用步进电动机时，往往会产生较大的细分角度误差，影响了步进运行的均匀性，而采用步进电动机细分专用驱动芯片时，要对步进电动机的相电流进行补偿比较困难。

随着半导体技术的发展，嵌入式微处理器的功能越来越丰富、性能越来越提高、价格越来越便宜，采用嵌入式微处理器为核心设计的二相步进电动机驱动器，可以方便地进行细分电流的自动补偿，其电路框图如图4 所示。其中嵌入式微处理器采用ST公司的M3 系列的ARM 处理器STM32F103，桥式功率放大器采用八只分立的VMOS 管IRF540 组成二个H 桥，VMOS 管的驱动由IR2104 来完成。

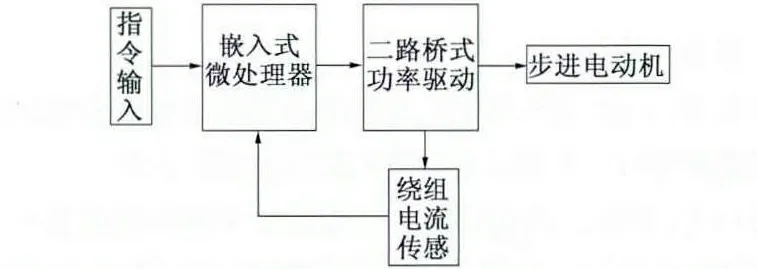
图4 细分驱动器系统框图

3 细分电路电流的自动补偿方法和试验结果

采用上述测出二相绕组通以细分量化的正交电流时的细分步距角与步进电动机的转子机械位置角之间的关系，然后进行插补求出补偿后的电流值，再写入程序中进行校验的方法比较繁琐，工作量较大。

针对这种情况，本文给出了一种细分电流的自动补偿办法，试验装置安装示意图如图5 所示。试验时用联轴器将步进电动机与编码器连接在一起，安装时尽量保证电机和编码器的同轴性。其中步进电动机驱动器采用图4 所示的驱动器;步进电动机为与图3 测试时所用同一电机，整步步距角为1.8°;编码器采用增量式光电编码器，型号为RI40K/35CQ，每圈脉冲数40 000，经微处理器STM32F103内部四倍频后分辨率可达8.1″。

图5 试验装置安装示意图

步进电动机细分自动补偿的软件框图如图6 所示。试验时设置补偿精度为0.012 5°、步进电动机细分数为16。上电后，首先在电机二相绕组中通以16 细分量化的正交电流，每一细分步时单片机均读取相对应的细分步距角，测出一组16 个步进电动机细分步距的数值，然后对细分电流进行插值求出细分电流的补偿值，然后使用补偿后的细分电流值再一次测量细分精度，如果补偿后精度达不到要求，则对补偿后的细分电流数值再次进行插值补偿，直至达到所期望的精度。

图6 自动补偿的软件框图

补偿后，采用日本小野公司的AP -370 测角仪和AM-610 信号处理器对步进电动机补偿后的步距角精度进行了测试，测试数据显示补偿后的最大细分误差为0.011 5°。补偿后的步距角和理论步距角对照如图7 所示，与图1 相比，自动补偿后的细分步距角精度提高了一个数量级。补偿后的绕组电流和理论电流对照如图8 所示。

图7 补偿后的步距角和理论步距角对比

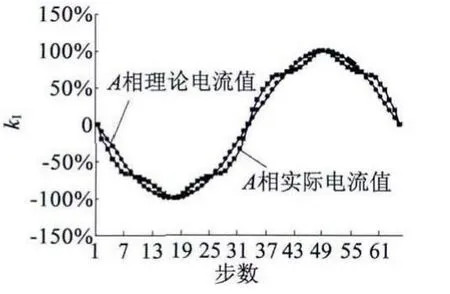
图8 补偿后的实际电流和理论电流对照

4 结 语

对于二相双极型混合式步进电动机的细分，由于不同的电机T/I 曲线的不同，因此需要采用不同的细分电流曲线来对其步距角进行细分。而试验表明，对于同一厂家的同一型号步进电动机，其补偿值基本相同，因此，在这种情况下只需要对一台电机进行补偿即可满足要求。

采用可编程驱动器进行自动补偿使得对细分电流的修正变得十分方便，在不增加硬件电路成本的情况下，大大减小了细分补偿的工作量，提高了步进电动机驱动器的性价比。

［1］ 王季秩，曲家骐. 执行电动机［M］. 北京:机械工业出版社，1997.

［2］ 坂本正文. 步进电机应用技术［M］.王自强，译.北京:科学出版社，2010.

［3］ Driving bipolar stepper motors using a medium-density STM32 -F103xx micro_controller［EB/OL］.http://www.st.com/st-web- ui/static/active/en/resource/technical/document/application _note/CD00207733.pdf.