水轮机影响域的数值仿真计算
2015-03-12韩端锋高良田
韩端锋,张 媛,高良田,孙 帅
(哈尔滨工程大学船舶工程学院,黑龙江哈尔滨150001)
0 引言
随着CFD技术的迅速发展,利用CFD对水轮机进行水动力性能数值模拟、叶片优化等方面的研究日趋成熟,计算精度也越来越高。
潮流能水轮机水动力性能直接关系到水轮机发电功率的大小,提高水轮机的水动力性能对水轮机的工程应用具有重要意义。试验分析、CFD方法和理论分析3种方法是目前研究潮流能水轮机性能的主要方法。英国Lunar公司[1]运用CFD方法分析了导流罩水轮机的水动力性能,对导流罩水轮机进行了1∶20水槽模型试验,验证了CFD方法的准确性;英国南安普顿大学可再生能源实验室的Bahaj等人从获能原理和试验分析的角度全面研究了水轮机特性,系统研究了水轮机效率、空化现象及波流耦合状态下水轮机水动力学性能,Bahaj[2]等的研究为潮流能水平轴水轮机的研究奠定了理论和试验基础。国内方面,北京风能分析小组和Glasgow海洋能小组[3]运用三维CFD模型研究了阵列水轮机性能与排布,分析了不同排布方式水轮机的水轮机水动力性能,描绘了机组尾流场的速度场。本文通过CFD方法,研究水轮机对周围流场的影响,主要为一种新型的海洋新能源综合发电平台 (见图1)的总布置提供必要的参考。
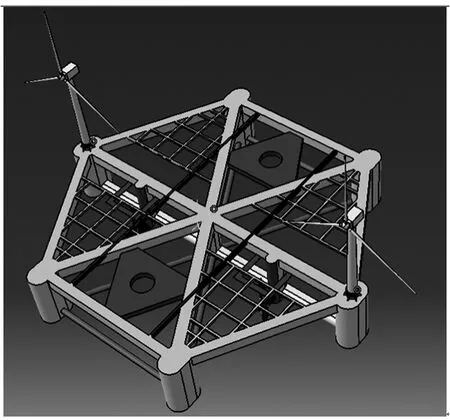
图1 海洋新能源综合发电平台Fig.1 Marine new energy integrated power generation platform
1 数学模型
计算流体动力学是通过计算机数值模拟及显示图像对包含有流体流动等物理现象的系统做分析。其主要思想是用一系列有限个离散点上的变量值的集合来代替原来在空间及时间域上连续的物理量的场,通过一定的方式和原则建立这些离散点上场变量之间关系的方程组,然后通过求解这些方程组得到场变量的近似值。它能够不受实际试验所需各种条件的限制,对计算对象进行离散和分析得出变量的近似值。本文主要是针对水轮机的流场进行分析。
1.1 控制方程
流体动力学的基本控制方程包括:质量守恒方程[3](连续性方程)、动量守恒方程和能量守恒方程。本文中的计算首先假定流体为不可压缩的流体,不涉及到求解能量守恒方程,对于牛顿流体而言,质量守恒方程和动量守恒方程的表达式为:
连续方程:
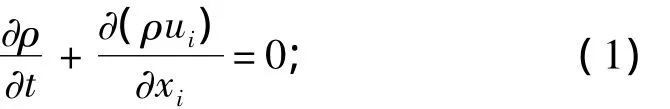
动量方程:

其他变量输运方程:
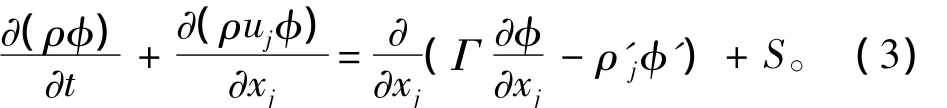
这里的(i,j)指标取值范围是 (1,2,3)。根据张量的有关规定,当某个表达式中一个指标重复出现2次,则表示要把该指标的取值范围内遍历求和。

这里,τij实际对应了6个不同的雷诺应力项,即3个正应力和3个切应力。
由式(1)~式(3)构成的方程共有5个方程 (雷诺应力为3个方程),而6个雷诺应力再加上原来的5个时均未知量 (ui,p,φ),总共有11个未知量,因此方程不封闭,必须引入新的湍流模型 (方程),才能使方程组封闭。这就涉及到后面的湍流模型。
1.2 湍流模型
湍流是指雷诺数大于临界值时,流动特征发生变化,流动成无序的这种状态。它是一种高度非线性的流动。为了研究这种流动,通常把它看做时间平均流动和瞬时脉动流动这2种流动的叠加。引入雷诺平均法经过转换就得到式(3)的雷诺时均N-S方程 (RNAS),然后通过引入湍流模型来封闭这个方程。
标准k-ω模型由于会在固壁上出现非物理的奇点,且不易处理避免附近变化剧烈的情况,Wilcox的k-ω被引入用于分析剪切流以及低雷诺数、可压缩性的流体。其控制方程为:
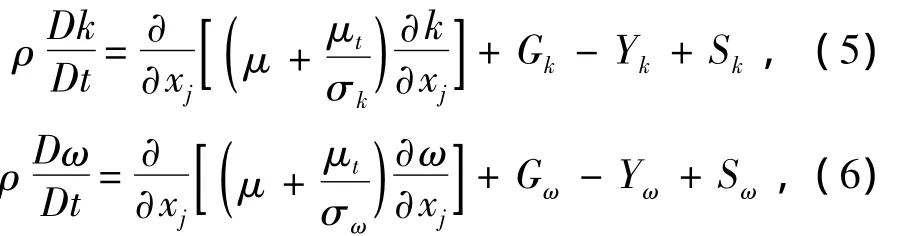
式中:Gk与Gω分别为层流速度梯度与湍流频率产生的湍动能;Yk与Yω为扩散产生的湍流;Sk与Sω为用户定义的源项。
该模型对于低雷诺数下的流动比标准k-ε模型具有更高的精度和数值稳定性。
1.3 数值计算方法
采用有限体积法对三维不可压缩RANS方程进行离散,压力速度耦合采用SIMPLEC算法进行计算。压力、密度以及动量各项采用一阶格式,为保证计算的收敛性,亚松弛因子均设置为0.2,设置残差小于0.000 01时结果收敛。
2 计算模型及网格划分
2.1 水轮机模型的建立和计算域的划分
数值模拟计算的第一步是建立精确的几何模型。它需要遵循在复合实际情况的前提下尽可能的简化模型。本文利用Catia软件,根据表1中提供的数据,建模得到水轮机的几何模型,如图2(a)所示。考虑到水轮机的旋转运动,计算域分为2个区域,内域和外域,内域为水轮机旋转区域,内含水轮机,外域为固定区域,为消除外域边界对水轮机水动力性能计算的影响,根据计算要求及模型尺寸建立恰当的控制域,使其在满足周围流场影响可忽略的情况下让控制域尽可能的小。这样可以在保证计算结果准确的前提下尽可能的提高计算效率。本文取叶片和桨毂的表面作为内边界面,取直径约为水轮机直径4倍的圆柱体表面看作是无穷远边界,作为外边界面,取水轮机直径1.1倍的小圆柱作为小域,便于进行局部加密。具体模型如图2(b)所示。

表1 潮流水轮机模型主要参数Tab.1 Geometry coefficients of the turbine
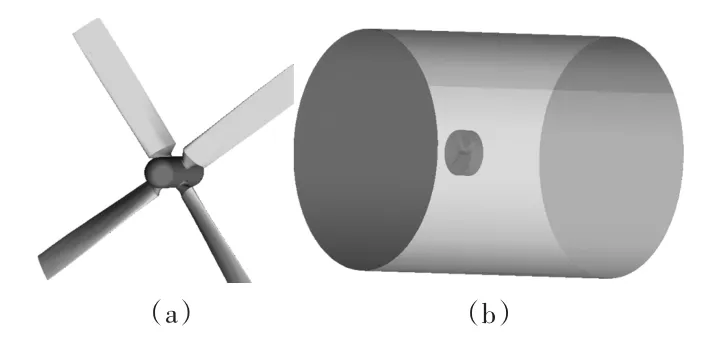
图2 水轮机几何模型和计算域Fig.2 Geometry model and calculation domain of turbine
2.2 网格划分
网格的离散划分是数值模拟中非常重要的工作,其好坏的程度将直接影响到求解的效率和精度。网格又分为结构和非结构网格两大类。结构网格适用于简单的模型,而对于复杂模型一般采用非结构网格。所以对于流场计算问题一般采用非结构网格,但是,全部使用非结构网格不仅网格质量不是很好,大扭曲率的网格数较多,影响计算精度,也影响计算效率。对于这种情况,一般把整个流场划分成几个子域,然后根据具体情况在每个子域上选则适当的网格类型。此外,网格的数目也是一个问题,网格过梳会导致结果不精确甚至错误;网格过密则会使计算时间过长,计算难于收敛。因此在网格划分过程中,我们需要合理安排网格数量,既要避免流场变化缓和区域的计算资源浪费又要避免流场变化大的区域网格过疏造成计算不准确,确保在节点数一定的情况下使用的网格模型能最大限度提高计算精度。另外,网格的划分是一项非常繁琐耗费时间的工作,需要不断的尝试,直到生成复合要求的网格。本文采用混合式网格,在小域内使用非结构网格,并对水轮机叶面及桨毂进行加密处理,在大域使用结构网格,提高计算效率,缩短计算时间,具体网格如图3所示。
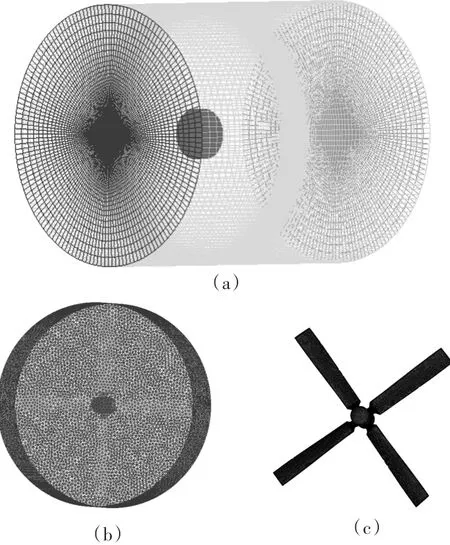
图3 网格的划分Fig.3 Mesh of the turbine
2.3 边界条件及参数的设定
边界条件是指位于求解域边界上的位置变量或其一阶导数随时间或者位置变化的规律只有选定合适的边界条件,才能获得流场正确的解。在Fluent中的基本边界条件有流动进出口边界,给定压力边界,壁面边界,对称边界,周期性边界。
进 (出)口边界指在进 (出)口指定流动参数的情况,一般可以设置速度、压力、质量进 (出)口边界,针对可压流动的质量进 (出)口边界在这里不适用。由于流场进行数值计算时,压力有相对值表示,实际求解相对于进口压力而言所以有时须给定压力参考值。壁面边界作为最常用的边界,采用它需修正压力方程,尤其对于湍流计算,近壁面湍流演变为层流,需对离散方程的源项做特殊处理。对于周期性运动采用周期性边界可以节约时间,提高计算效率。
由于水轮机在流体中运动时,流体不能与桨叶(毂)面分离又不能穿透桨叶 (毂)面,因此必须要求流体质点在桨叶 (毂)面运动的法向分量与桨叶 (毂)面运动的法向分量相同。其次,水轮机置于无限大的流场中运动时,远处的流体基本不受扰动,此时可认为流体仍保持静止状态。再次,由于不对尾流做研究可以假定尾涡面的厚度为零并且无流体和压力降穿过尾涡面并且根据Kelwin涡量守恒条件得知流场中的涡不会消失。最后,要满足库塔条件即认为随边叶面和叶背的压力差为0,随边速度为有限值。
因此,针对此流场,在Fluent中将来流的入口设为速度入口,根据海域流速情况,选择海域平均流速2.2 m/s为入口速度,将出口设为自由流动。此外,将大域即整个流场设为无滑移壁面,而将水轮机设为滑移壁面与小域一起运动。
在设定边界条件后,选择SIMPLEC算法,剪切压力传输 (SST)k-ω模型形成封闭的控制方程,然后通过设置求解的控制参数,初始化流场解得数值模拟的计算结果。
3 计算结果分析
3.1 水轮机影响域计算
图3为水轮机轴向截面流速分布云图,该图直观地显示了水轮机在尾流区域的流动速度变化情况。由图中可看出,水轮机对轴向方向上的速度影响范围较大,在径向方向上影响范围较小;在叶梢位置形成一高速区,由于轮毂的阻碍作用,轴向速度迅速减小;尾流在水轮机的下游持续较长,由图5可知,距离轮毂中心位置越近,则速度恢复较慢;轮毂中心线处,由于轮毂的阻碍作用,轴向速度迅速减小为0,然后沿尾流方向,速度逐渐恢复;在距离水轮机1.5D时,尾流速度为入口流速的63%;在距离水轮机2.5D时,尾流速度为入口流速的88%;叶尖位置处,在距离水轮机4D时,尾流速度为入口流速的93%;距离轮毂中心线0.5R处,沿尾流方向,速度先减小后恢复,其恢复较快。
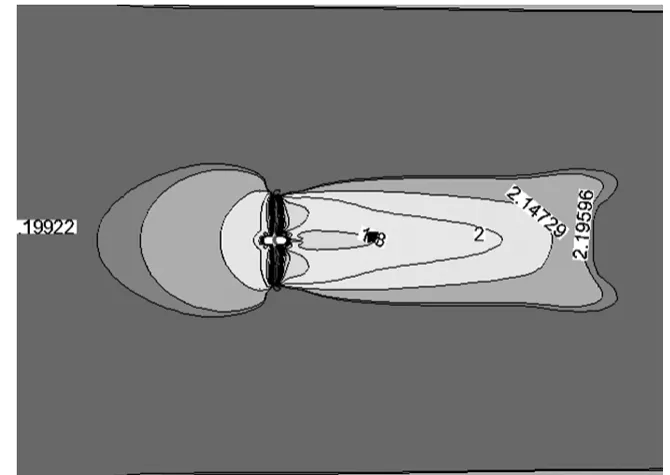
图4 单个水轮机影响域计算结果Fig.4 The influence domain calculation results of single turbine

图5 不同位置轴向速度分布Fig.5 The distribution of axial velocity
3.2 水轮机间距对受力的影响
在相同的条件下,改变两水轮机的横向距离,进行相关模拟计算[4],得到水轮机距离分别为叶片直径的1.5,2,3倍时水轮机受力情况,表2为两水轮机受到的轴向力和转矩值。

表2 不同间距下两水轮机所受轴向力和转矩值Tab.2 The axial force and the torque
由表2可看出,两水轮机距离大于2倍直径时,各水轮机的受力值在数值上接近单个水轮机的受力值,水轮机的距离对轴向力和转矩的影响非常小,可忽略不计;而当水轮机间距为1.5 D时,对水轮机性能影响较大,两水轮机轴向力及转矩均有所减小。
3.3 水轮机间距对尾流场的影响
由图6可看出,当2个水轮机的间距为2倍直径时,两水轮机尾流速度之间几乎没有干扰;而当水轮机间距缩小为1.5 D时,两水轮机尾流方向速度存在较大的相互干扰,导致受影响的尾流区域相对变大。
为更好地描述水轮机工作的性能参数,选择以下特征系数来表示:
水轮机从海流中获取的能量用能量系数Cp表示,是评价水轮机性能最重要的参数,其表达式为:

式中:P为功率;V为水流速度;R为叶片半径。
为研究水轮机在不同转速下的特性,定义叶尖速比为λω,其表达式为:

式中ω为水轮机角速度。

图6 水轮机间距对尾流场的影响Fig.6 The influence of turbine spacing on the wake flow field

图7 水轮机性能曲线Fig.7 The performance of turbine
由图7可知,采用CFD数值模拟得到的结果与实验值[6]趋势相同,最大误差在5%左右;当尖速比为3.4时,试验值与数值计算值的Cp均开始下降。CFD方法可以较为准确得出水轮机的性能趋势和最大效率,相比于试验方法,CFD方法更加简洁,成本较低,且能够更加准确地捕捉水轮机周围流场细节,对工程应用具有一定的指导作用。当2个水轮机间距为2D时,水轮机效率较单个水轮机效率略有减小,而当间距减小为1.5D时,效率进一步下降,尤其是当尖速比增大时,效率下降明显。说明随着水轮机转速的增加,水轮机间相互干扰加强。
4 结语
本文首先对流体流动的基本概念与相关流动模型做了简单介绍,对Fluent软件的基本结构、数值求解方法和求解过程做了概述。其次,采用k-ε湍流模型结合混合网格技术开展了水轮机敞水性能预报,计算了水平轴水轮机的水动力性能,并对水轮机周围流场情况作了简要分析,讨论了水轮机的安放间距对水轮机性能和流场的影响,研究发现,当水轮机间距为1.5 D时,水轮机之间的相互影响较大,水轮机性能下降,间距为2 D时,水轮机相互之间几乎没有影响。
[1] KERWIN JE,TAYLOR T E,BLACK SD,et al.A JSME Fluids Engineering,July 6-11,2003,Honolulu,Hawaii:ASME,2003:1-7.
[2] BAHAJ A S,BATTEN W M J,MCCANN G.Experimental verifications of numerical predictions for the hydrodynamic performance of horizontal axis marine current turbines.Renewable Energy,2007,32:2479 -2490.
[3] BAI L,ROY R G S,GREGORY D.Investagation of influence of array arrangement and spacing on tidal energy converter performance using a 3-Dimensional CFD model.
[4] 陈存福.潮流能水平轴水轮机叶片优化及水动力性能研究[D].青岛:中国海洋大学,2012.CHEN Cun-fu.Study on blade optimization and hydrodynamic performance of horizontal axis marine current turbine[D].Qingdao:Ocean University of China,2012.
[5] 刘志华,熊鹰,叶金铭,等.基于多块网格混合的RANS
方法预报螺旋桨水动力性能的研究[J].水动力学研究与进展,2007,22(4):450 -456.LIU Zhi-hua,XIONG Ying,YE Jin-ming,et al.Based on hybrid RANSmethod of forecast of the grid block propeller hydrodynamic performance research[J].Water Dynamics Research and Development,2007,22(4):450 -450.
[6] 安佰娜.潮流能发电场尾流场数值模拟及其多机组影响规律研究[D].青岛:中国海洋大学,2012.An Bai-na.Numerical Analysis of the Wake and Interaction Effect Analysis for tidal arrays in the Tidal Farm[D].Qingdao:Ocean University of China,2012.
[7] 王福军.计算流体动力学分析[M].北京:清华大学出版社,2004.WANG Fu-jun.Computational fluid dynamics analysis[M].Beijing:Tsinghua University Press,2004.
