横风对涡环旋转伞系统运动的影响

马晓冬 刘荣忠 郭锐 吕胜涛

（南京理工大学机械工程学院，智能弹药技术国防重点学科实验室，南京 210094）

0 引言

涡环旋转伞是一种常见的旋转降落伞，伞衣的高速旋转，使得带涡环旋转伞的物伞系统在下降时具有良好的稳定性。此外，它还具有阻力系数大、开伞动载小、易维护等优点，广泛应用于兵器的弹道控制、飞机的着陆减速和控制、空降空投、航天飞行器的安全回收技术以及外太空的探险和着陆等领域[1-2]。

作为一种常见的气动力减速器，降落伞的下落运动状态很大程度上易受风的影响。文献[3]以灾难环境下翼伞空投机器人系统为背景，建立翼伞系统六自由度的简化运动模型，设置常值侧风的仿真环境，分析了风对系统的影响；文献[4]对某型号飞船在几种不同风场条件下的回收过程进行仿真研究，分析了风对返回舱各项参数的影响；文献[5]针对某型弹射座椅建立考虑风速的弹射过程动力学模型，选取不同风速风向和不同弹射速度作为计算状态，对弹射救生过程进行数值仿真，分析了风对弹射座椅救生性能的影响；文献[6-8]研究了复杂风场条件下伞降系统的定点回收和航迹规划问题。

本文利用伞塔投放实验数据和理论运动模型，对涡环旋转伞的气动力参数进行识别，并在此基础上，计算横风影响下的弹道规律，并与高塔实验数据进行对比分析。通过改变横风速度，得到涡环旋转伞系统在横风作用下的运动规律。

1 伞物系统运动模型

1.1 模型的建立

本文研究的涡环旋转伞系统主要由4部分组成，包括涡环旋转伞、伞盘、旋转接头和载物[9]，如图1所示。涡环旋转伞的结构复杂，一般由4片伞衣幅和多根不同长度的伞绳连接而成。伞衣幅上不对称的开口设计可以实现在充满的情况下，形成一定的凸面和倾斜度，在不对称空气动力和力矩的作用下实现旋转性能，伞盘通过旋转接头带动载物旋转。

本文主要研究涡环旋转伞系统受横风作用的横向运动，为简化问题，作如下假设：

1）假设涡环旋转伞充满后形状不再变化，涡环旋转伞与载物之间刚性连接；

2）关注涡环旋转伞系统水平方向和竖直方向上的平移运动；

3）只考虑涡环旋转伞的气动力。

1.2 运动方程的建立

涡环旋转伞系统运动模型如图2所示。图中O-xyz为大地坐标系；O为初始时刻系统质心位置；轴Oz方向竖直向下；轴Ox水平且指向系统运动方向；轴Oy由右手定则确定； O1-x1y1z1为系统轴坐标系；O1为系统质心；轴O1z1方向沿伞轴向下；轴O1x1垂直于伞轴指向运动方向；Oc和Op分别为涡环旋转伞和载物的质心；Lc为伞质心到系统质心的距离；Lp为载物质心到系统质心的距离；θ为伞轴与铅垂轴的夹角。

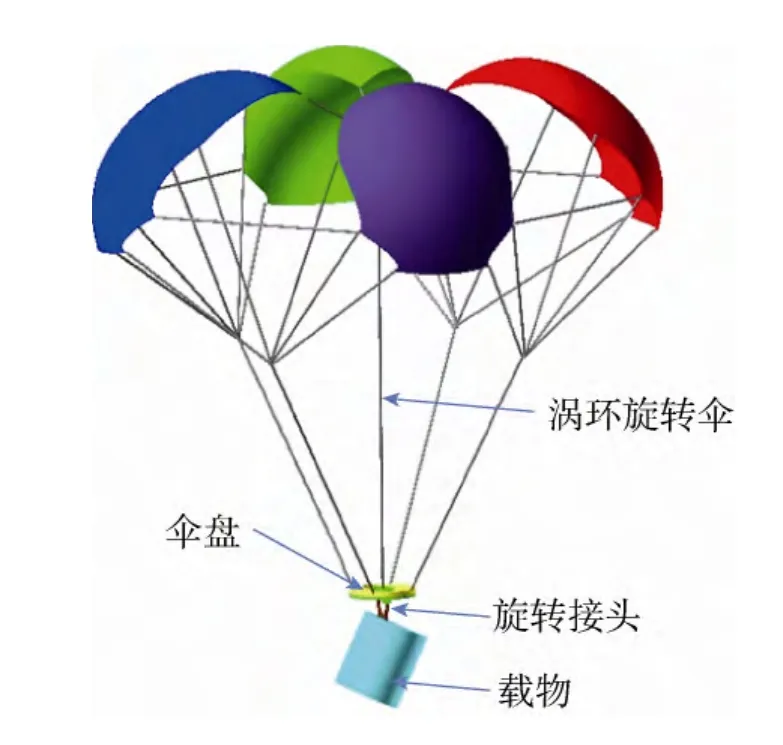
图1 涡环旋转伞—载物系统Fig.1 Vortex ring parachute-payload system

图2 涡环旋转伞系统运动模型Fig.2 Motion model of vortex ring parachute system

涡环旋转伞系统的4自由度弹道方程为

2 伞塔实验

2.1 实验环境与条件

伞物系统实验模型从高塔顶部100m处投放，初始落速和转速均为0。实验用的高速录像机为Red lake dk100，拍摄频率为1kHz，照片尺寸为640×480像素，距投放点地面投影100m。标志物为铅垂放置且有固定尺寸刻度的绳索，如图3所示，通过测量底部标志物B点的实际高度确定各标志物的高度。图中，A和B为标志物的顶部点和底部点，P为载物底部点；xA、xB和xP分别为A、B和P在图片中像素的横坐标；zA、zB和zP分别为A、B和P在图片中像素的纵坐标；XA、XB和XP分别为A、B和P距离地面原点的水平距离；ZA、ZB和ZP分别为A、B和P距离地面原点的高度。为准确记录伞物系统下落时间和转速变化，在载物上装有姿态参数存储测量仪[10]。

图3 正在下落的涡环旋转伞—载物系统Fig.3 Falling vortex ring parachute-payload system

2.2 数据提取

（1）基于图像提取涡环旋转伞系统运动轨迹

涡环旋转伞系统自由飞行时间较短，天空背景几乎不变，利用Surendra算法[11]提取高速摄影图片中的天空背景。选取系统在视场中的高速摄影图片序列，与天空背景差分并去噪后得到伞物系统运动图像序列[12-14]，最终得到涡环旋转伞系统的上下左右像素极值，可由载物下缘像素坐标来确定伞物系统的位置和运动。

图3中，AB之间的连线垂直于地面，假设点A的地面投影为原点，则XA=XB=0，可得：

设高速录像的频率为f，伞物系统抛出后拍摄第一张图像的时刻为t1，则在拍摄的第n张图片中，伞物系统的飞行时间为t1+n/f，P距地面原点的水平距离和高度为Xp,n和Zp,n。选取一系列的高速录像图片，可确定伞物系统飞行时间向量T及对应的水平距离向量Xtest和高度向量Ztest。

（2）基于姿态储存测量仪提取转速

载物内部装有姿态参数存储测量仪，实验结束后读取测量仪中的数据，可得到涡环旋转伞系统在下落过程中的转速变化和飞行时间，具体见文献[10]。

3 结果与分析

3.1 涡环旋转伞系统的气动力参数

当涡环旋转伞系统达到稳定状态时，ωy=0，θ=0，且 Vr=V - Vw=0，本文只考虑水平横风的作用，则Vx=Vw。由T和Xtest可得到涡环旋转伞系统的水平速度序列，如图4所示，由图可见，系统水平速度大部分计算值约为3.19m/s，其它值有较大的偏离。原因如下：进行伞塔实验时，为了使伞物系统的运动过程尽量在高速录像机的视场中，可将高速录像机布置在距离伞塔较远位置，由于其分辨率相对较低，因此图片中伞物系统的轮廓较模糊。在提取载物下缘坐标序列时，不可能每次都选择同一位置，导致水平速度值产生波动，因此在本次实验中，当水平速度约为3m/s时，即认为涡环旋转伞系统达到稳定运动状态。将该速度序列的平均值作为涡环旋转伞系统的水平稳定速度，即横风速度，得 Vx=Vw=3.19m/s。

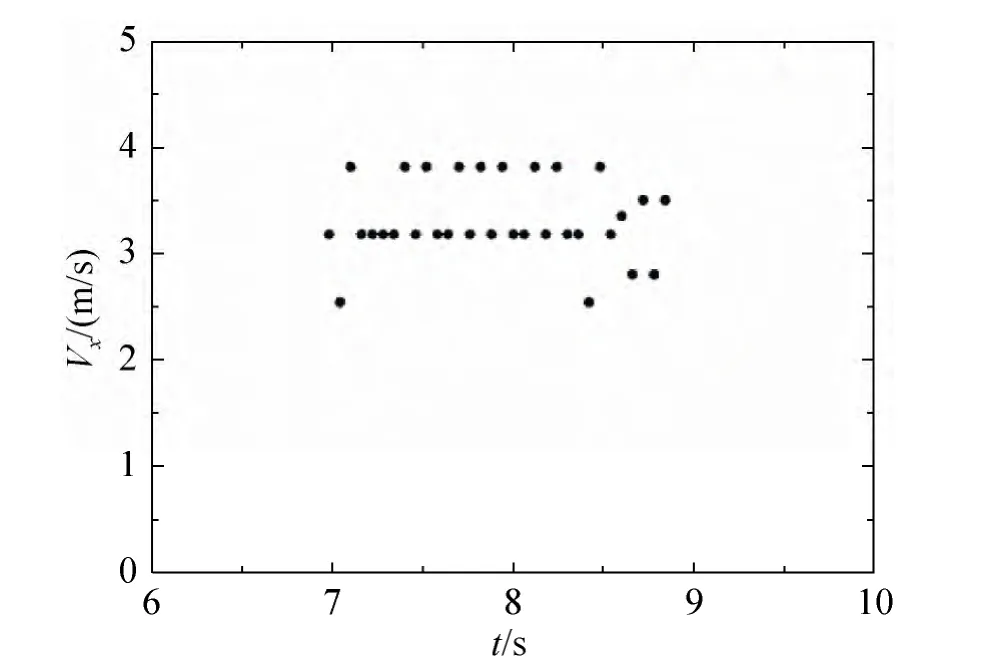
图4 伞塔实验的系统水平速度序列Fig.4 Horizontal velocity sequence of tower test

涡环旋转伞系统的主要参数为：mc=0.35kg，mp=10.5kg，L=1.7m，S=1.19m2，Iy=1.04kg·m2， Iz=0.07kg·m2。为研究涡环旋转伞系统的弹道特性，根据文献[15-16]，设CT=CT0，CN=CN0⋅α，其中CT0和CN0为常数，α为系统攻角；CR0和CRd无法通过伞塔实验数据获取，故利用计算流体力学方法得到CR0=0.87，CRd=0.31。利用龙格—库塔法对4自由度运动方程进行求解，利用遗传算法[16]对涡环旋转伞的气动力参数进行识别，其中目标函数为

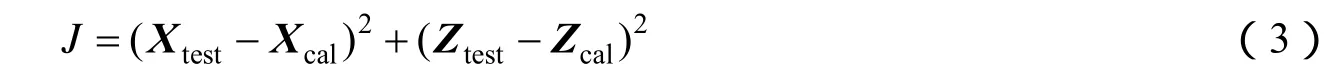
式中 Xcal和Zcal分别为理论计算得到水平位移序列和高度序列。

在上述参数设置下，经过仿真分析发现，通过遗传算法可准确地识别出涡环旋转伞的轴向力系数CT=1.02。由于伞塔实验中涡环旋转伞系统在水平方向上经过很短的时间内就达到稳定，高速录像机捕捉到的图像中系统水平速度已与风速一致，因此通过水平位移序列不能有效地识别出法向力系数。

文献[15]中指出，轴向力和法向力系数与阻力和升力系数存在以下关系：

式中 CD和CL分别为阻力和升力系数。在小攻角条件下，sinα≈α，cosα=1，且忽略升力，CD为常数，则有：CT=CD=1.02，CN=CDα=1.02α，CN0=CD。

将上述气动力参数代入式（1）中，可求得系统弹道规律。涡环旋转伞系统水平位移和高度变化的理论值及实验值如图5～6所示，理论值和实验值的吻合较好。涡环旋转伞系统下落过程中的转速变化情况如图7所示，可见t ≈3s时理论值达到稳定值3.30r/s，实验中系统的稳定转速在3.30r/s附近浮动，二者吻合较好。因此，本文建立的4自由运动模型可在一定程度上反映涡环旋转伞系统的真实运动情况。

图5 涡环旋转伞系统水平位移Fig.5 Horizontal displacement

图6 涡环旋转伞系统落高度变化Fig.6 Altitude change

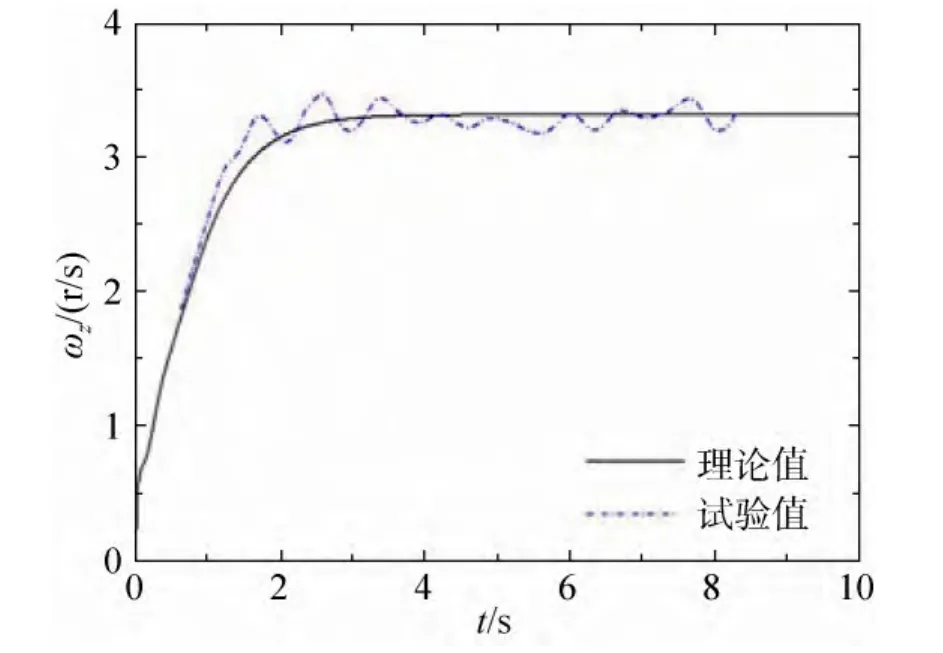
图7 涡环旋转伞系统转速变化Fig.7 Spinning rate change

3.2 横风对涡环旋转伞系统运动的影响

为了更直观地分析横风对涡环旋转伞系统运动的影响，设置初始条件：系统初速 V0=0； ωz= 0；（x0,z0）=（0,100m）。改变Vw大小，对式（1）进行求解，得到系统运动变化规律。

横风对系统水平速度和下落速度的影响规律如图8～9所示。由图8可以看出，在横风的作用下，涡环旋转伞系统Vx从0开始增大，其值最终达到Vw。Vx极值稍大于稳定值，这是由初始偏角θ和横风使系统在运动开始阶段发生摆动引起的。Vw越大，Vx达到稳定的时间越长。由图9可以看出，与Vx情况类似，由于θ的存在，对 Vz的影响较大，在初始的一段时间内，Vw越大 Vz的增速越慢，当 Vw=10m/s时，Vz出现负值，即受风影响系统向上方运动约0.6s。系统z方向的加速度在不同风速下大致相同，Vw越大，Vz达到稳定的时间越长。

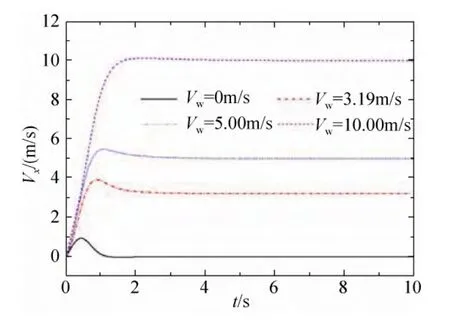
图8 风速对系统水平速度的影响Fig.8 Effect of wind on horizontal velocity

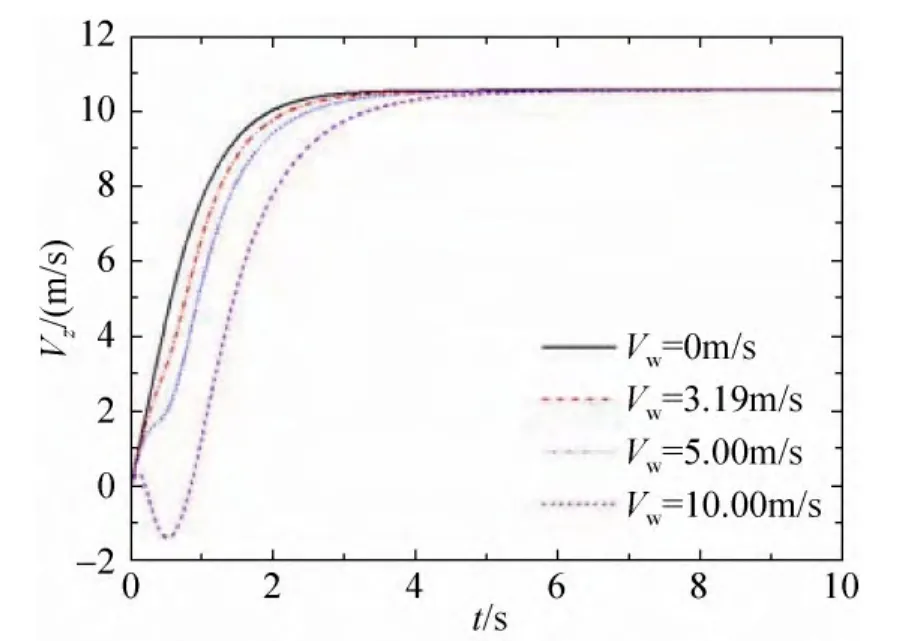
图9 风速对系统下落速度的影响Fig.9 Effect of wind on vertical velocity

横风对涡环旋转伞系统转速变化的影响如图10所示。系统的稳定转速与风速大小无关，这是由于结构确定的涡环旋转伞具有恒定的转速落速比，Vz稳定值不变，则zω稳定值也不变。在初始的一段时间内，受Vw的影响zω急剧增大，且Vw越大zω越大。t ≈1.6s时，不同风速影响下的zω数值趋于一致，逐渐达到稳定状态。

风速对侧向力的影响规律如图11所示。由于Vx能在2s内达到风速，因此Fx亦在2s内衰减至0。显然，侧向力远小于载物重力，所以根据式（1）判断可知，系统的摆动角不会在平衡位置附近发生大范围的多次震荡，理论计算结果如图12所示。但Vw越大，摆动角的极值越大。0～10s涡环旋转伞系统的空间运动轨迹如图13所示，显然其水平方向的运动受横风影响严重。

图10 风速对伞系统转速的影响Fig.10 Effect of wind on rotating speed

图11 风速对侧向力的影响Fig.11 Effect of wind on lateral force

图12 风速对摆动角的影响Fig.12 Effect of wind on swing angel

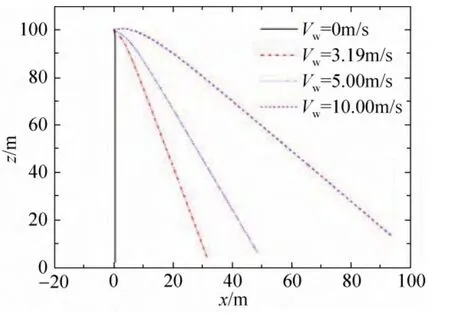
图13 风速对运动轨迹（0～10s）的影响Fig.13 Effect of wind on trajectory（0～10s）

3.3 实际工况

涡环旋转伞的一个重要作用就是减速和导旋，其展开充满开始工作时，伞物系统已具有一定的初速和转速。为了解涡环旋转伞系统实际工作情况，设置初始条件：V0=（36.7m/s，41.6m/s），ωz0=14.2m/s，（x0, z0）=（0, 200m）。

实际工况和不同横风条件下涡环旋转伞系统的水平速度和下落速度变化曲线如图14～15所示。由图14可以看出，在不同风向和风速条件下，Vx均在较短的时间内达到稳定值Vw，这是由于初始速度V0值较大，使得相对速度Vr较大，侧向力Fx较大，因此系统在水平方向上具有较大的加速度。由图15可以看出：在运动初始阶段，Vz大幅增加，这主要由式（1）中的ωyVx项引起。当Vx较大时会发生此种情况，而Vx较小时Vz不会增大。当Vw不同时，Vz达到稳定的时间差别不大。但在顺风时Vw越大及逆风时Vw越小的情况下，Vz变化越平缓。

在给定实际工况的初始条件下，涡环旋转伞系统的转速变化受横风风速的影响不明显，与Vz类似，zω在运动开始阶段会小幅度地增大，如图16所示。由于Vx和Vz在很短时间内达到稳定，因此涡环旋转伞系统的运动轨迹除起始阶段外，其余近似直线，且系统稳定后的运动轨迹与上节中的情况类似，如图17所示。

图14 风速对系统水平速度的影响Fig.14 Effect of wind on horizontal velocity

图15 风速对系统下落速度的影响Fig.15 Effect of wind on vertical velocity

图16 风速对系统转速的影响Fig.16 Effect of wind on rotating speed

图17 风速对系统运动轨迹（0～10s）的影响Fig.17 Effect of wind on trajectory（0～10s）

4 结束语

1）通过 Surendra方法提取涡环旋转伞系统背景图像，对高速录像拍摄的图像进行运动目标提取，获得系统下落时间、高度向量及水平距离向量，结合运动模型，利用遗传算法对涡环旋转伞系统的气动力参数进行识别。该方法简单、快速、有效，可用于其他类型伞物系统。

2）涡环旋转伞的轴向力系数为1.02，大于一般其他类型伞。

3）在横风作用下，涡环旋转伞系统产生横向漂移；在气动力和载物重力的共同作用下，系统不会发生多次震荡和摇摆；水平速度和下落速度在较短的时间内达到稳定值，风速越大，稳定时间越长；实际工况下，较大的水平初始速度会导致下落速度和转速在短时间内的增大。

4）对于结构确定的涡环旋转伞系统，横风不会影响其稳定落速和转速；在实际工况下，横风几乎对转速变化无影响。

5）本文分析了横风对涡环旋转伞系统运动的影响，但理论模型较简单。后续工作将建立涡环旋转伞系统的多体动力学模型，详细探究横风对涡环旋转伞和载物运动及二者间相对运动的影响。

（

）

[1] 王利荣. 降落伞理论与应用[M]. 北京: 宇航出版社, 1997. WANG Lirong. The Theory and Application of Parachute[M]. Beijing: Astronautics Press, 1997. （in Chinese）

[2] Ewing E G, Bixbu H W, Knacke T W. Recovery Systems Design Guide[R].Gardena: Irvin Industries Inc., 1978.

[3] 焦亮, 孙青林, 亢晓峰. 翼伞空投机器人系统的六自由度仿真[J]. 计算机仿真, 2011, 28（1）: 39-42. JIAO Liang, SUN Qinglin, KANG Xiaofeng. Simulation of 6-DOF Parafoil and Air-dropped Robot System[J]. Computer Simulation, 2011, 28（1）: 39-42. （in Chinese）

[4] 廖前芳, 程文科, 宋旭民, 等. 风场对舱—伞系统着陆姿态影响的仿真研究[J]. 航天返回与遥感, 2005, 26（2）: 6-10. LIAO Qianfang, CHENG Wenke, SONG Xumin, et al. The Simulation Study of Wind Influence on Attitude of Landing of Cabin-parachute Systems[J]. Spacecraft Recovery & Remote Sensing, 2005, 26（2）: 6-10. （in Chinese）

[5] 郁嘉, 毛晓东, 林贵平, 等. 风对弹射座椅救生性能的影响[J]. 航空学报, 2013, 34（4）: 727-740. YU Jia, MAO Xiaodong, LIN Guiping, et al. Impact of Wind on Ejection Seat Escape Performance[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34（4）: 727-740. （in Chinese）

[6] 席庆彪, 张波, 田小雄, 等. 基于风场估测的无人机伞降定点回收研究[J]. 西北工业大学学报, 2004, 22（4）: 452-456. XI Qingbiao, ZHANF Bo, TIAN Xiaoxiong, et al. On Navigation Control of UAV in Recovery Stage to Ensure Reliable Parachute Landing on Assigned Spot with Wind Disturbance Estimation Considered[J]. Journal of Northwestern Polytechnical University, 2004, 22（4）: 452-456. （in Chinese）

[7] 孙守明, 李恒年, 王海涛, 等. 基于回收着陆段精细模型的飞船落点预报[J]. 飞行力学, 2013, 31（2）: 143-147. SUN Shouming, LI Hengnian, WANG Haitao, et al. Landing Point Prediction of Spacecraft Based on Fine Model of Recovery and Landing System[J]. Flight Dynamics, 2013, 31（2）: 143-147. （in Chinese）

[8] 于海涛, 陈楸, 李德荣, 等. 基于 Bezier和改进 PSO算法的风环境下翼伞航迹规划[J]. 电子设计工程, 2014, 22（19）: 28-34. YU Haitao, CHEN Qiu, LI Derong, et al. Route Planning of Parafoil Airdrop System in Complex Wind Field[J]. Electronic Design Engineering, 2014, 22（19）: 28-34. （in Chinese）

[9] 马晓冬, 刘荣忠, 郭锐, 等. 涡环旋转伞系统开伞充气过程仿真研究[J]. 航天返回与遥感, 2013, 34（2）: 1-8. MA Xiaodong, LIU Rongzhong, GUO Rui, et al. Simulation Research on Inflation of Vortex Rotating Parachute System[J]. Spacecraft Recovery & Remote Sensing, 2013, 34（2）: 1-8. （in Chinese）

[10] 郭锐, 刘荣忠, 胡志鹏, 等. 涡环旋转伞开伞稳定性及减速导旋运动特性研究[J]. 空气动力学学报, 2013, 31（6）: 733-738. GUO Rui, LIU Rongzhong, HU Zhipeng, et al. Study on the Inflated Stability and Motional Characteristics of Vortex Ring Parachute Canopy[J]. Acta Aerodynamica Sinica, 2013, 31（6）: 733-738. （in Chinese）

[11] 王正勤, 刘富强. 自适应背景崎岖算法的比较[J]. 计算机工程, 2008, 34（23）: 220-223. WANG Zhengqin, LIU Fuqiang. Comparison of Adaptive Extract Algorithm of Object Scene[J]. Computer Engineering, 2008, 34（23）: 220-223. （in Chinese）

[12] 范盈, 郭成安. 一种运动图像的检测与识别技术[J]. 大连理工大学学报, 2004, 44（1）: 122-126. FAN Ying, GUO Cheng’an. A Method for Detection and Recognition of Moving Objects in Sequential Images[J]. Journal of Dalian University of Technology, 2004, 44（1）: 122-126. （in Chinese）

[13] 刘贵喜, 绍明礼, 刘先红, 等. 真实场景下视频运动目标自动提取方法[J]. 光学学报, 2006, 26（8）: 1150-1155. LIU Guixi, SHAO Mingli, LIU Xianhong, et al. Video Moving Object Auto-extraction in Real Scene[J]. Acta Optica Sinica, 2006, 26（8）: 1150-1155. （in Chinese）

[14] 胡志鹏, 刘荣忠, 郭锐, 等. 基于弹丸图像的末敏弹阻力系数计算方法[J]. 探测与控制学报, 2012, 34（3）: 8-12. HU Zhipeng, LIU Rongzhong, GUO Rui, et al. TSP Drag Coefficient Calculation Based on Projectile Image Processing[J]. Journal of Detection & Control, 2012, 34（3）: 8-12. （in Chinese）

[15] Doherr K F. Nine-degree-of Freedom Simulation of Rotating Parachute Systems[J]. Journal of Aircraft, 1992, 29（5）: 774-781.

[16] 王海涛, 郭叔伟, 郭鹏, 等. 遗传算法在大型降落伞气动力参数识别中的应用[J]. 宇航学报, 2010, 31（4）: 981-985. WANG Haitao, GUO Shuwei, GUO Peng, et al. Application of Genetic Algorithms for Aerodynamic Parameter Estimation of Large Parachute[J]. Journal of Astronautics, 2010, 31（4）: 981-985. （in Chinese）