弯扭组合载荷下圆轴表面裂纹应力强度因子计算

张 宇，黄小平，闫小顺

(1．上海交通大学海洋工程国家重点实验室，上海200240;2．中国舰船研究设计中心，湖北武汉430064)

0 引言

轴类构件在船舶结构中有许多应用，如用作螺旋桨轴等。这些构件需承受周期性的应力，并因此导致疲劳等结构损伤而提前失效。在传统的设计思想中，人们通常把构件材料视作无缺陷的连续均匀体，只根据S－N曲线来估计疲劳寿命，并不考虑裂纹萌生和裂纹扩展的时间，然而在实际结构中，初始裂纹或者缺陷无法避免。已有研究表明，由表面缺陷引起的结构断裂是轴类构件失效的主要原因之一。随着断裂力学的发展，现在已经可以通过研究疲劳裂纹的扩展行为来更准确地预测构件的疲劳寿命。应力强度因子作为判断结构断裂和裂纹扩展的重要参数，也日益引起了人们的重视。

当前，对于轴类或者管类构件表面裂纹的研究，多集中在拉弯载荷下的Ⅰ型应力强度因子上［1－6］。对于许多轴类构件来说，除了承受外力和自身重量所引起的弯曲应力之外，还要承受扭转载荷，因此计算弯扭组合载荷下表面裂纹的扩展寿命更有意义。由于弯扭组合载荷下的裂纹不再是单一的张开型裂纹，而是复合型裂纹，相关的研究要少得多，且对表面点应力强度因子计算存在较大误差［7－9］。本文在前人研究成果的基础上，以含半椭圆表面裂纹的实心圆轴为研究对象，对裂纹体网格划分进行了改进，运用插值方法得到了裂纹表面点处的应力强度因子，研究了扭转载荷下裂纹形状对应力强度因子的影响，以及裂缝前缘各点Ⅱ、Ⅲ型应力强度因子沿裂缝前缘的分布规律，并探讨了弯、扭组合载荷下同型应力强度因子叠加原理的有效性。从而为评估该类裂纹的扩展寿命提供参考。

1 复杂载荷下的应力强度因子计算

三维裂纹形状如图1所示，x方向是裂纹正前方，y方向是裂纹面法线方向，z方向和裂纹面平行。考虑一个离裂端很近，位置在极坐标 (r，θ)的单元，根据弹性力学，可以将裂纹尖端的位移场表示为:

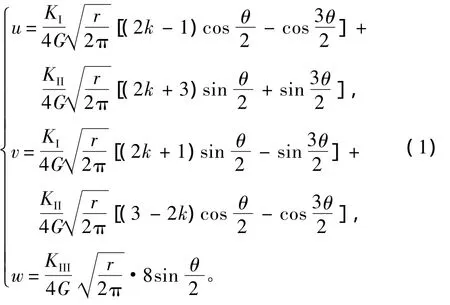
式中:u，v，w 分别为直角坐标系中 x，y，z方向的位移分量;r和θ为极坐标系下的2个坐标分量，且r的值远小于裂纹长度。G为剪切模量，G=E/2(1+μ)，κ为与材料泊松比μ有关的常数，对于平面应变问题，κ=3－4μ;对于平面应力问题，κ=(3－μ)/(1－μ)。KI，KII，KIII分别是 I，II，III型应力强度因子。由于裂纹前缘绝大部分范围为平面应变状态，平面应力状态只在紧靠自由表面的一个很小的区域内存在。因此，本文取κ=3－4μ。

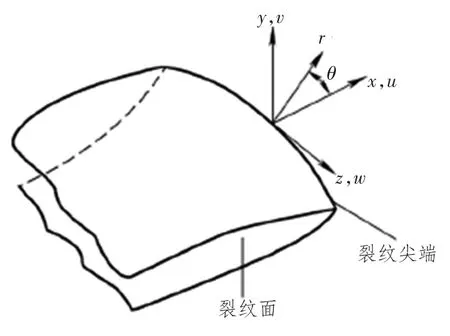
图1 三维裂纹模型Fig.1 Three dimensional crack model

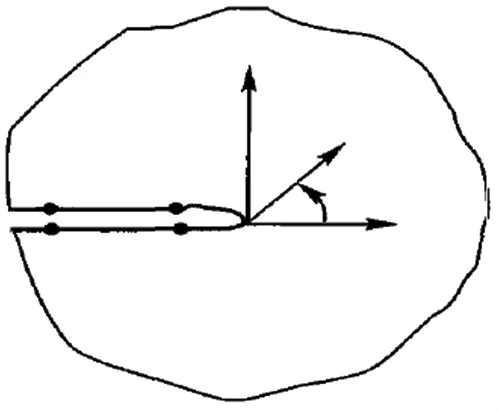
图2 定义求解路径Fig.2 Defined path for solving the SIFs

根据式(1)，如果裂纹表面上(θ=180°)某一点的位移已知，那么可以得到:

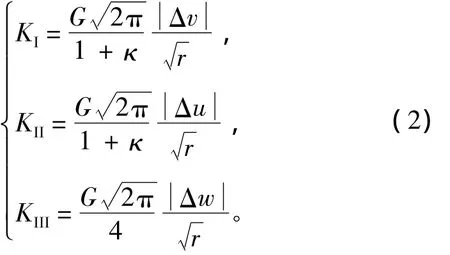
式中:Δu，Δv，Δw分别为2个裂纹面之间沿x，y，z方向的相对位移。在用Ansys自带命令kcalc计算应力强度因子时，需要定义各个节点处的局部坐标系和计算路径，并且要求局部坐标系的x轴垂直于裂纹前缘，y轴垂直于裂纹所在平面，求解路径如图2所示。在得到2～5点的相对位移之后，代入式(2)，即可得到这些节点处的应力强度因子。然后再利用最小二乘法，即可外推得到裂纹尖端处的各型应力强度因子的数值解。

为了使所研究的应力强度因子变化规律具有普适性，这里对应力强度因子进行无量纲化处理，无量纲应力强度因子表示如下:

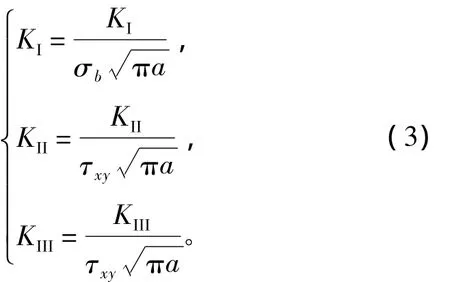
式中:σb为弯曲应力;τxy为圆轴表面最大剪切应力;a为裂纹深度。对于实心圆轴来说，弯曲应力σb=，剪切应力;M为施加的弯矩;T为施加的扭矩。

2 有限元分析

2.1 模型基本参数

本文中，计算所使用的实心圆轴直径d=50 mm，长度l=300 mm，裂纹在圆轴中部，裂纹所在横截面如图3所示。用无量纲参数a/d和a/c描述裂纹形状，其中，a/d为裂纹相对深度，a/c为裂纹形状比。a，c分别为裂纹深度和裂纹长度，β为裂纹面与圆轴表面的交角，称为裂纹嵌入角。用x/h来表示裂纹前缘上任意一点D的相对位置，h为裂纹宽度，x为裂纹前缘上D点的横坐标。a/c变化范围为0.2～1.0，a/d的变化范围取为0.05～0.5，x/h的变化范围为0～1.0。考虑到扭转载荷的不对称性，建立的模型为全模型，建模时采用商用有限元软件Ansys14.0。为了适应裂纹尖端节点处的应力奇异性，裂纹前缘采用1/4 20节点等参退化奇异单元。对于圆轴的其他部分，则采用等参三维六面体单元solid95进行自由网格划分，含裂纹的实心圆轴有限元模型如图4所示。材料弹性模量为E=210 000 MPa，泊松比μ=0.3。

在施加弯矩或者扭矩时，本文采用cerig命令的方式，在构件中心位置建立一个节点，定义为mass21单元，将该节点和其他受力节点耦合，形成刚性区域，然后在该节点上直接施加力矩。图5是弯矩加载示意图。圆轴另一端施加全约束，边界条件如图6所示。

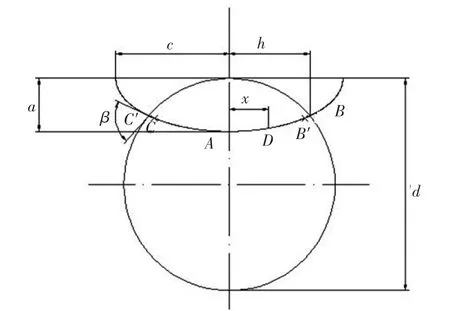
图3 裂纹所在横截面Fig.3 Geometry of semi-elliptical surface crack

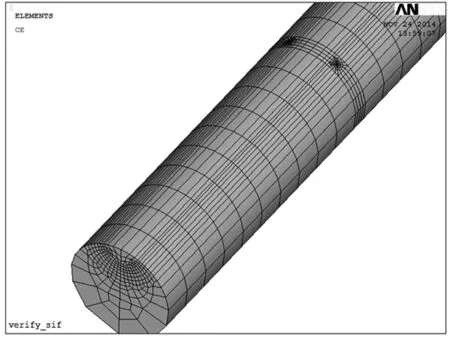
图4 实心圆轴有限元模型Fig.4 Finite element model of shaft

图5 弯矩加载Fig.5 Applied bending moment by using mass21 element

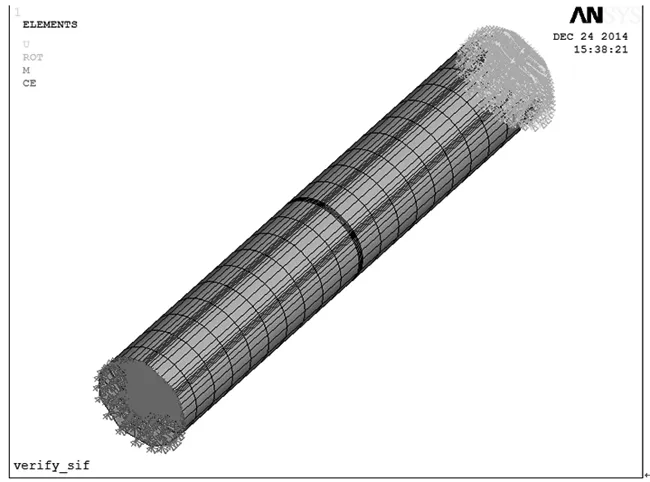
图6 载荷及边界条件Fig.6 Loading and boundary conditions

2.2 裂纹体网格划分

在第1节中已经提到，用Ansys自带命令计算裂纹前缘各节点的应力强度因子时，需要首先定义合适的局部坐标系和求解路径。在目前常用的裂纹体网格划分中，通常是由面单元拖拉形成整个裂纹体单元［10］，如图7所示。然而这种方法无法保证裂纹前缘各节点处局部坐标系中的x轴垂直于裂纹前缘。由式(2)可知，在求解Ⅰ型应力强度因子时，仅需要y轴方向的相对位移Δv。只要局部坐标系的y轴方向垂直于裂纹所在平面，即可得到比较准确的KI值。求解Ⅱ，Ⅲ型应力强度因子时，则需要局部坐标系下的x，z方向的相对位移Δu，Δw，如果局部坐标系设定不合理，KII，KIII的求解结果会产生很大的误差。

为此，本文对裂纹体网格划分方法作了如下改进:将裂纹体切割成两部分，再分别对这2个部分进行网格划分，如图8所示。从而使除了表面点附近区域外的裂纹前缘各节点处局部坐标系中的x轴尽量垂直于裂纹前缘。网格划分方法改进前后裂纹前缘各节点的局部坐标系对比如图9所示。当a/c=0.4，a/d=0.1时，分别对裂纹体网格划分改进前后的模型施加弯曲和扭转载荷，计算得到KI，KII，KIII沿着裂纹前缘的分布规律如图10所示。可以看到，网格划分改进与否对于KI的影响很小，而对于裂纹前缘上的各点来说，愈靠近表面点处，网格划分对局部坐标系中x轴的方向影响愈大，从而对KII，KIII的计算结果的影响也愈大。需要指出的是，改进后的网格划分方法仍然无法保证每一个局部坐标系的x轴都完全垂直于裂纹前缘，但和改进前的网格划分方法相比，相对而言要更加合理，下文中均采用改进后的网格划分方法。

图7 常规裂纹体网格划分Fig.7 Regular crack meshing

图8 改进网格划分方法后的裂纹体模型Fig.8 Crack model after improving meshing method

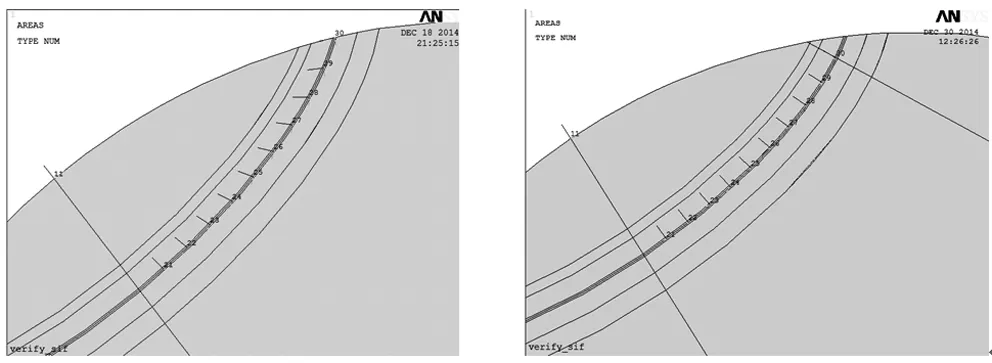
图9 网格划分改进前后裂纹前缘各节点局部坐标系对比Fig.9 Local coordinate system comparison between regular crack meshing and changed crack meshing

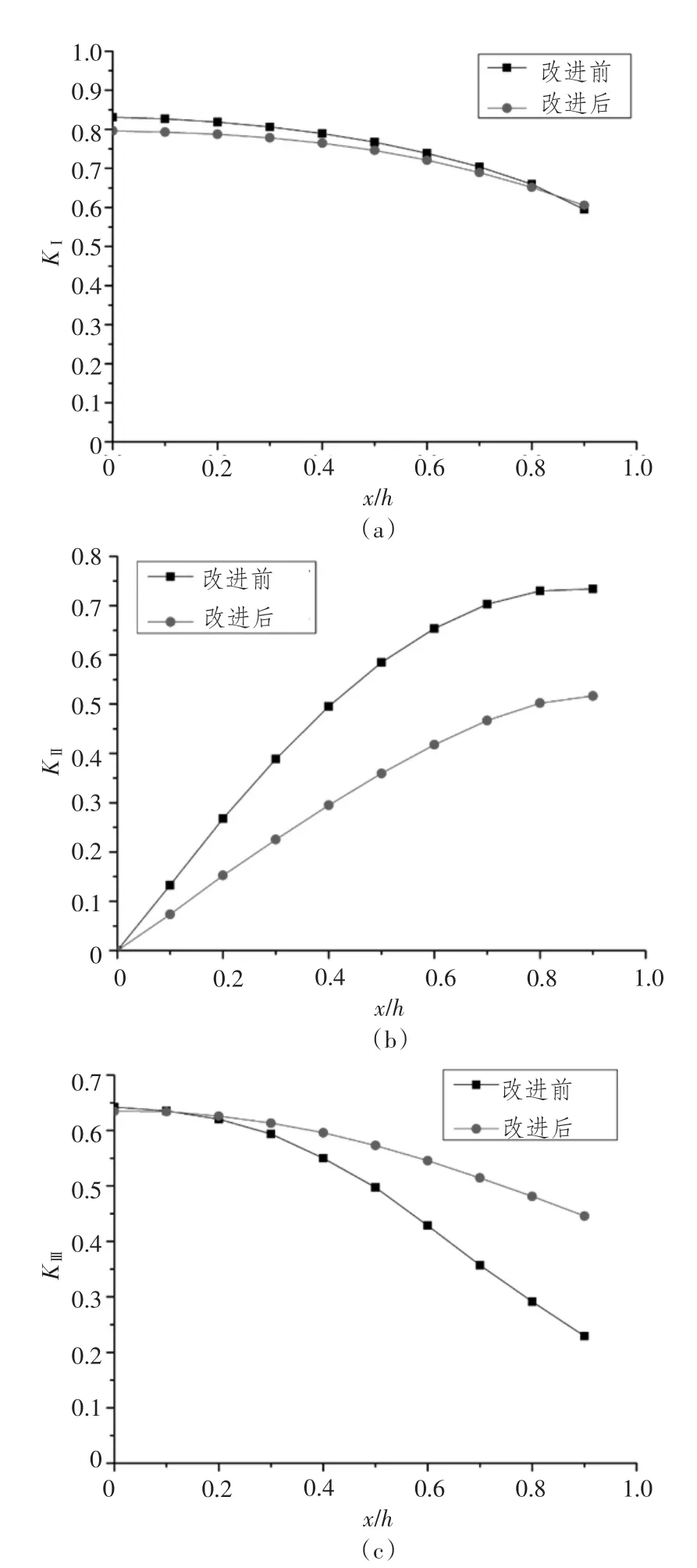
图10 K I、K II、K III沿裂缝前缘分布对比(a/c=0.4，a/d=0.1)Fig.10 The comparison of K I，K II，K III along crack surface

2.3 模型验证

为了验证上述模型以及网格划分的正确性，本文计算了在弯曲载荷下，裂纹形状比a/c=1.0时最深点A处和近表面点B'处的Ⅰ型应力强度因子，并 和 Murakami［3］， Shih ＆ Chen［4］， Couroneau ＆Royer［11］等的计算结果进行对比，如图11所示。对比结果显示，最深点的无量纲应力强度因子KI与Murakami，Shih＆Chen以及Couroneau＆Royer等人的计算结果基本相符，误差极小，只有裂纹深度很小时误差才大于3.0%;对于近表面点B'处，本文的结果和已有文献的平均值相比，误差基本不超过5%，且变化趋势和上述文献相同，从而证明了本文建模以及应力强度因子求解方法的正确性。

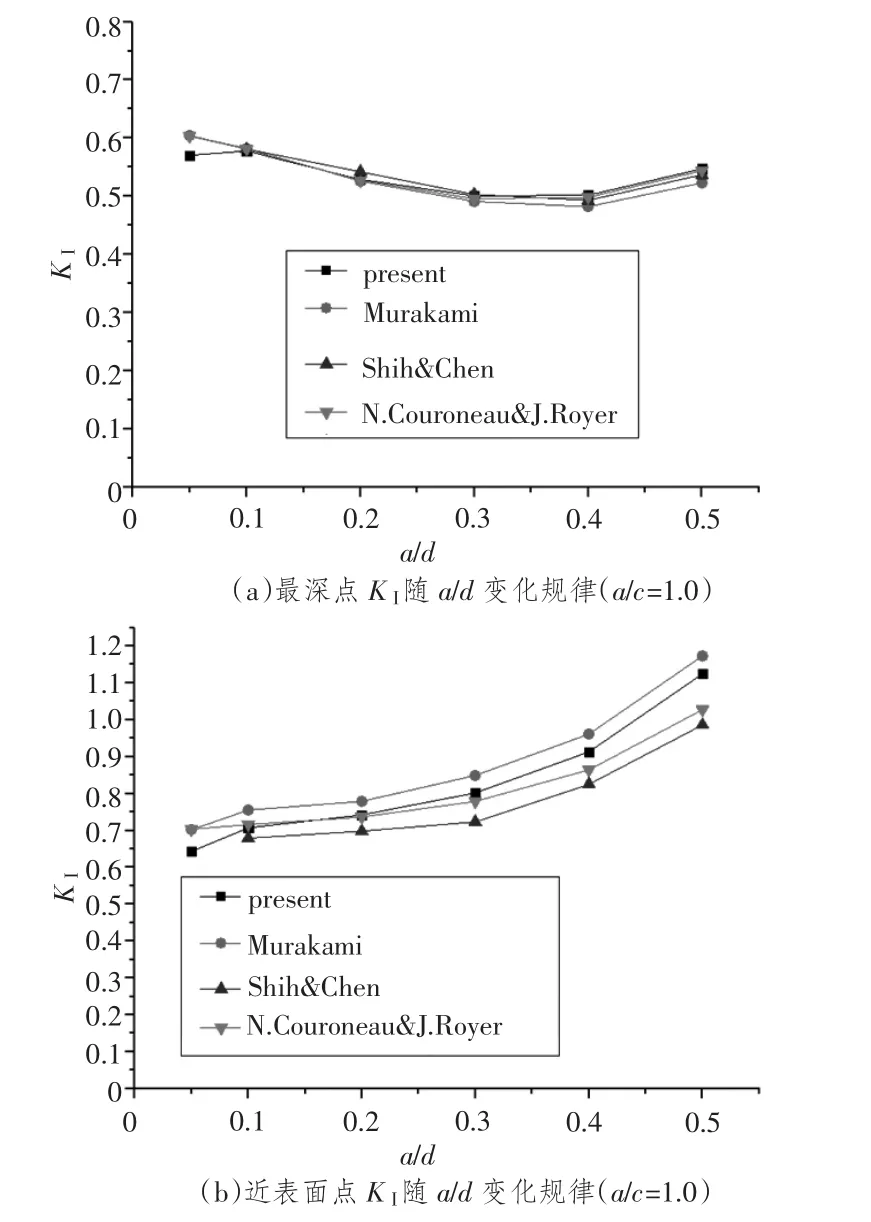
图11 弯曲载荷下应力强度因子对比结果Fig.11 Comparison of SIFs under bending loading

2.4 表面点应力强度因子处理

有必要指出，线弹性断裂力学的主要假设之一是裂纹前缘的连续性，对于裂纹前缘和几何体自由表面的交点，即裂纹的表面端点来说，这一假设不再适用［7］。已经有人从断裂能量的角度出发，在理论上证明了在裂纹表面端点附近，应力奇异性的次数取决于材料泊松比 μ 以及裂纹嵌入角 β［12－13］。Pook指出，在用三维有限元方法分析含有裂纹的几何体时，所得到的裂纹表面端点附近的断裂力学参数不可信。对于裂纹表面端点来说，运用退化1/4节点单元来模拟应力和应变的奇异性并不能得到准确的结果。当裂纹嵌入角β很小时，表面点处的应力强度因子会突然趋向于0，而在裂纹嵌入角β很大时，表面点处的应力强度因子会突然趋向于无穷大。但是这种突变只发生于表面端点附近很小的区域之中［12］。在已有的文献里，人们在研究Ⅱ、Ⅲ型应力强度因子沿裂纹前缘的分布时，通常避开这一区域，将x/h的最大值取在0.8～0.9之间［9］。然而对于构件疲劳寿命预报来说，裂纹表面点的应力强度因子非常重要。考虑到应力强度因子沿裂缝前缘分布的连续性，本文采用插值方法外插得到表面点处的各型应力强度因子，从而将x/h的取值范围拓展到0～1.0。

3 结果分析与讨论

3.1 扭转载荷

对模型施加扭转载荷后，本文计算了裂纹前缘各点的Ⅱ、Ⅲ型无量纲应力强度因子KII，KIII。当裂纹形状比a/c=1.0，a/d=0.05～0.5时，KII，

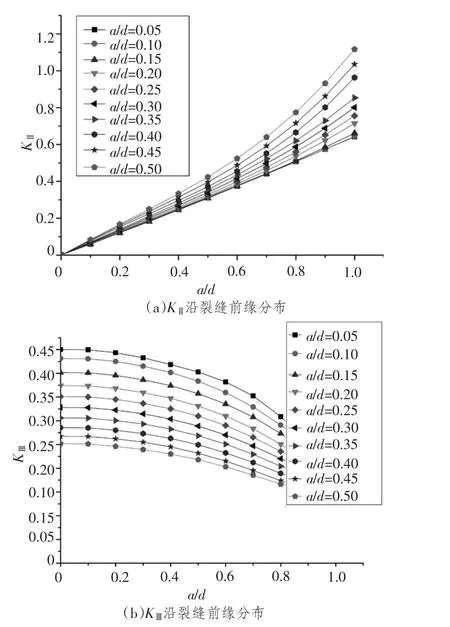
图12 各型应力强度因子沿裂缝前缘分布Fig.12 K I，K II variation along the crack surface

KIII沿着裂缝前缘的分布如图12所示。从图中可以看到，除最深点外，裂纹前缘上其他各点均同时存在KII和KIII，说明扭转载荷下裂纹并不是单一型裂纹，而是II－III型复合裂纹。KII在裂缝最深点为0，沿裂缝前缘随着x/h的增大而逐渐增大，且随着裂纹相对深度的增加，其增长速度逐渐变快;KIII在裂纹最深处达到最大值，沿着裂缝前缘随x/h的增加而逐渐减小。

对于裂纹最深点，在扭转载荷下，只有KIII存在，随着相对深度a/d的增加，KIII逐渐减小;随着裂纹形状比a/c的增加，KIII逐渐减小。其变化规律如图13和图14所示。

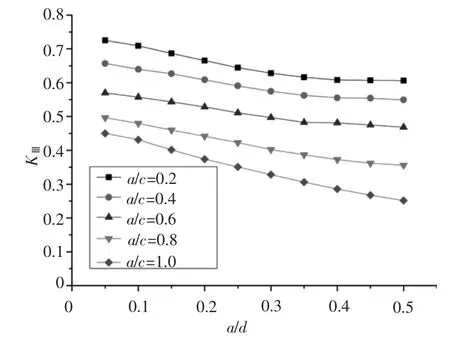
图13 最深点K III随a/d变化Fig.13 K III variation with a/d at deepest point

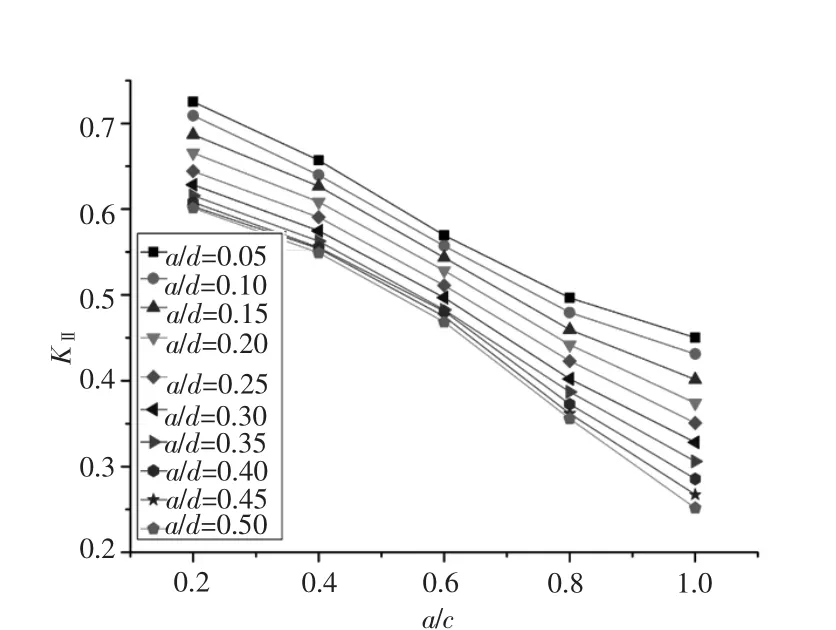
图14 最深点K III随a/c变化Fig.14 K III variation with a/c at deepest point

3.2 弯扭组合载荷

在裂纹形状比a/c=1.0，相对深度比a/d=0.1时，本文分别计算了弯曲、扭转和弯扭组合载荷这3种载荷情况下的各型应力强度因子。3种载荷下的KI，KII，KIII沿裂纹前缘分布对比分别如表1～表3所示。可以看到，在计算表面裂纹的应力强度因子时，弯扭组合载荷可以视作弯曲载荷和扭转载荷的简单叠加，两者之间相互影响可以忽略。如果已知弯曲载荷和扭转载荷下的应力强度因子经验公式，可以直接用于求解弯扭组合载荷下的各型应力强度因子，从而避免复杂耗时的有限元计算。

表1 K I沿裂纹前缘分布对比(a/c=1.0，a/d=0.1)Tab.1 K I variation along the crack surface(a/c=1.0，a/d=0.1)

表2 K II沿裂纹前缘分布对比(a/c=1.0，a/d=0.1)Tab.2 K II variation along the crack surface(a/c=1.0，a/d=0.1)

表3 K III沿裂纹前缘分布对比(a/c=1.0，a/d=0.1)Tab.3 K III variation along the crack surface(a/c=1.0，a/d=0.1)

4 结语

本文采用三维有限元方法，对弯曲、扭转和弯扭组合载荷下实心圆轴表面裂纹应力强度因子进行了研究，主要研究内容和结论如下:

1)对裂纹体网格划分进行了改进，使得裂纹前缘各点的Ⅱ，Ⅲ型应力强度因子计算结果更加准确。

2)基于应力强度因子沿着裂缝前缘分布的连续性，运用插值方法外插得到表面点处的应力强度因子。

3)扭转载荷之下的裂纹是Ⅱ－Ⅲ型复合裂纹，在裂纹最深点只有Ⅲ型应力强度因子存在，且最深点Ⅲ型应力强度因子随着裂纹相对深度a/d的增大而减小，随着裂纹形状比a/c的增大而减小。裂缝前缘除最深点外均同时存在Ⅱ型和Ⅲ型应力强度因子，随着x/h的增大，Ⅱ型应力强度因子占比逐渐增大。

4)弯扭组合载荷下的裂纹是Ⅰ－Ⅱ－Ⅲ型复合裂纹，裂纹前缘各点的Ⅰ、Ⅱ、Ⅲ型应力强度因子可以视作分别施加弯曲载荷和扭转载荷下裂纹前缘相同位置的同型应力强度因子的叠加。本结论可为弯扭组合载荷下轴类构件疲劳寿命预报提供参考。

［1］ RAJU I S，NEWMAN J C．Stress intensity factors for circumferential surface cracks in pipes and rods under tension and bending loads［J］．Fracture Mechanics，1986，17:789－805．

［2］ SHIRATORI M，MIYOSHIT，SAKAY Y，et al．Analysis and application of influence coefficients for round bar with a semi-elliptical surface crack［M］．In:Murakami Y，editor．Stress Intensity Factors Handbook， Vol II．Oxford:Pergamon Press，1987:659 － 65．

［3］ MURAKAMI Y，TSURU H．Stress intensity factor equations for semi-elliptical surface crack in a shaft under bending［M］．In:Murakami Y，editor．Stress Intensity Factors Handbook，Vol II．Oxford:Pergamon Press，1987:657 －8．

［4］ SHIH Y S，CHEN JJ．The stress intensity factor study of an elliptical cracked shaft［J］．Nuclear Engineering and Design，2002，214:137 －145．

［5］ CARPINTERI A，BRIGHENTI R．Fatigue propagation of surface flaws in round bars:a three-parameter theoretical model［J］．Fatigue ＆ Fracture of Engineering Materials ＆Structures，1996，19(12):1471 －1480．

［6］ TOBIRIO J．A critical review of stress intensity factor solutions for surface cracks in round bars subjected to tension loading［J］．Engineering Fatigue Analysis，2009，16(3):794－809．

［7］ MANUAL DA F，MANUEL DE F．Stress intensity factor for semi－elliptical surface cracks in round bars under bending and torsion［J］．Journal of Fatigue，1999，21(5):457－463．

［8］ SHAHANI R，HABIBI S E．Stress intensity factors in a hollow cylinder containing a circumferential semi-elliptical crack subjected to combined loading［J］．International Journal of Fatigue，2007，29:128 －140．

［9］ ISMAIL A E，ARIFFIN A K，ABDULLAH S，et al．Stress intensity factors under combined tension and torsion loadings［J］．Indian Journal of Engineering ＆ Materials Sciences，2012，19:5 －16．

［10］瞿伟廉，鲁丽君，李明．带三维穿透裂纹结构的有限元实体建模方法［J］．武汉理工大学学报，2008，30(1):87－90．QUE Wei-lian，LU Li-jun，LI Ming．Solid modeling method for structure with 3 － D straight through crack［J］．Journal of Wuhan University of Technology，2008，30(1):87 －90．

［11］ COURONEAU N，ROYER J．Simplified model for the fatigue growth analysis of surface cracks in round bars under mode I［J］．Journal of Fatigue，1998，20(10):711－718．

［12］ POOK L P．On fatigue crack paths［J］．Journal of Fatigue，1995，17(1):5 －13．

［13］王效贵，郭乙木，许金泉．与界面相交的裂纹尖端的应力奇异性分析［J］．固体力学学报，2002，23(4):412 －418．WANG Xiao-gui，GUO Yi-mu，XU Jin-quan．On the stress singularity of crack terminating at the interface［J］．Acta Mechanica Solida Sinica，2002，23(4):412 －418．