交叉口处轨道交通与常规公交的换乘模型研究
2015-03-11孙凡松张开冉王若成
孙凡松 张开冉 王若成
西南交通大学,交通运输与物流学院,成都610031
0 引 言
国内外关于轨道交通换乘问题的研究较多,大致上分为以下几类:第一类研究主要是通过对轨道交通换乘方式的比例进行对比分析,根据区域适应性不同选择最优的换乘方式[1-3];第二类研究是针对轨道交通车站换乘客流、行为特征以及换乘客流路径进行,然后对具体的换乘设备设施进行设计[4];第三类则主要通过选取步行距离、延误时间、换乘次数等指标进行计算和分析,给出了轨道交通和其他方式交通衔接的建议和指导[5]。
上述的研究往往是从整体着手,对轨道交通出入口处各种交通出行方式进行分类,选定换乘的效率和经济性等指标进行研究。本文研究发现,在交叉口处尚存在轨道交通站点到常规公交的走行距离过长、轨道交通与常规公交时间匹配度不高、换乘站的设置不合理等衔接换乘问题,并且对于交叉口处既有常规公交和轨道交通的换乘优化问题也尚未得到妥善解决。因此,交叉口处轨道交通与常规公交的换乘模型设计对目前解决交叉口处的交通拥堵问题会有很大的帮助。
本文通过对轨道交通出入口客流换乘方式的比例分析和常规公交停靠站位置比选,在综合考虑各种影响因素的情况下进行主成分分析,建立了交叉口处轨道交通与常规公交的换乘模型。
1 轨道交通车站客流换乘方式比例分析
通过对出行者出行方式选择影响因素的分析[6],结合全国各大城市居民使用轨道交通出行的调查结果,将与轨道交通衔接的其他交通方式分为常规公交、出租车、私家车、摩托车、自行车、步行、其他交通方式七种,其具体比例如表1所示。

表1 轨道交通车站客流换乘方式比例分布Tab.1 Transfer proportion distribution of rail transit station passenger flow
由表1可见,除日常步行方式外,公交衔接所占的比例尤为突出,占总体的 1/4,并且这个比例还在不断扩大,同时,这也是建立城市客运一体化研究的重点之一。找出公交和轨道交通的衔接特征,提高二者的衔接服务水平和配套的政策支持,才能更好地推动公交系统的建立进程。
2 常规公交停靠站位置比选
通过实地调研常规公交停靠站的布设位置,发现设置情况主要分为路段设置和交叉口设置两种方式,每种设置方式均有各自的特点。
将路段和交叉口两种位置进行比较[5,6],如表 2所示,由于在路段是否设置行人过街设施对换乘乘客的安全性有较大影响,故把路段分为有行人设施和无行人设施两种情况。

表2 路段和交叉口设站的位置比选Tab.2 Comparison of road section and intersection station location
可见,在设有行人过街设施的路段设置公交站要明显优于交叉口设站和未设行人过街设施的路段设站,但其缺点在于不方便乘客的换乘,而在交叉口设站的优点又恰恰在于方便乘客换乘。考虑到设有行人过街设施的路段较为少见以及城市公交换乘体系的建立,常规公交站大多设置在交叉口附近。
3 既有公交站优化设计的影响因素分析
目前,我国的轨道交通尚处在初步发展阶段,除了有限的几个特大城市以外,其他城市的轨道交通尚未形成网络,所以本文主要讨论的是轨道交通单线站台与接运的常规公交系统的换乘;另外,由于轨道交通相对于常规公交起步较晚,故在轨道交通建成后,相应交叉口处的常规公交就存在最佳换乘的优化问题。对于城市交叉口处的换乘优化,具体的换乘影响因素如表3所示。

表3 既有公交站换乘因素表Tab.3 The existing bus station transfer factors
对于以上列出的各种交叉口换乘的影响因素,采用调查问卷的方式(采取百分制)对交叉口处的行人进行问卷调查,得到各个因素的影响参数值分别为η1、η2、η3、η4、η5、η6,进行标准化处理后采用 Matlab进行回归分析,得到一个6×N的矩阵:

得到初始矩阵后,对调查数据进行变量的标准化:
X=X';
Stdr=std(x);
[n,m]=size(x);
Sddata=x/stdr(ones(n,1):);
在进行调查数据标准化后,采用 Matlab的princomp指令来进行优化过程中影响因素的主成分分析:
[p,princ,egenvalue]=princomp(sddata);
p3=p(:,1:3);
Sc=princ(:,1:3);
egenvalue
Per=100·egenvalue/sum(egenvalue);
由此得到前三位的主成分系数和主成分得分,并且进一步得到各个主成分的贡献率p1、p2和p3。这样,对于不同的特定交叉口,可以相对客观地得到既有公交优化后的主要影响因素和标准化后所得到的贡献率。对于交叉口既有公交站优化的情况,因平均小时客流量的变化会对衔接模型产生影响,所以在建立模型的时候需要考虑增加一个如下所示的调整系数ε:

式中:Px,y——点(x,y)的平均小时客流量;
pi——此前得出的各个主成分的贡献率。
4 轨道交通站点与常规公交站点换乘设计
4.1 常规公交站点设计流程
根据轨道交通和常规公交的吸引范围,确定轨道交通站点附近可能的公交站点集,并选择有代表性的点集进行研究,建立相应的数学模型和目标函数。对有代表性的点进行求解,找出最优或较优的站点设置位置。设计流程如图1所示。
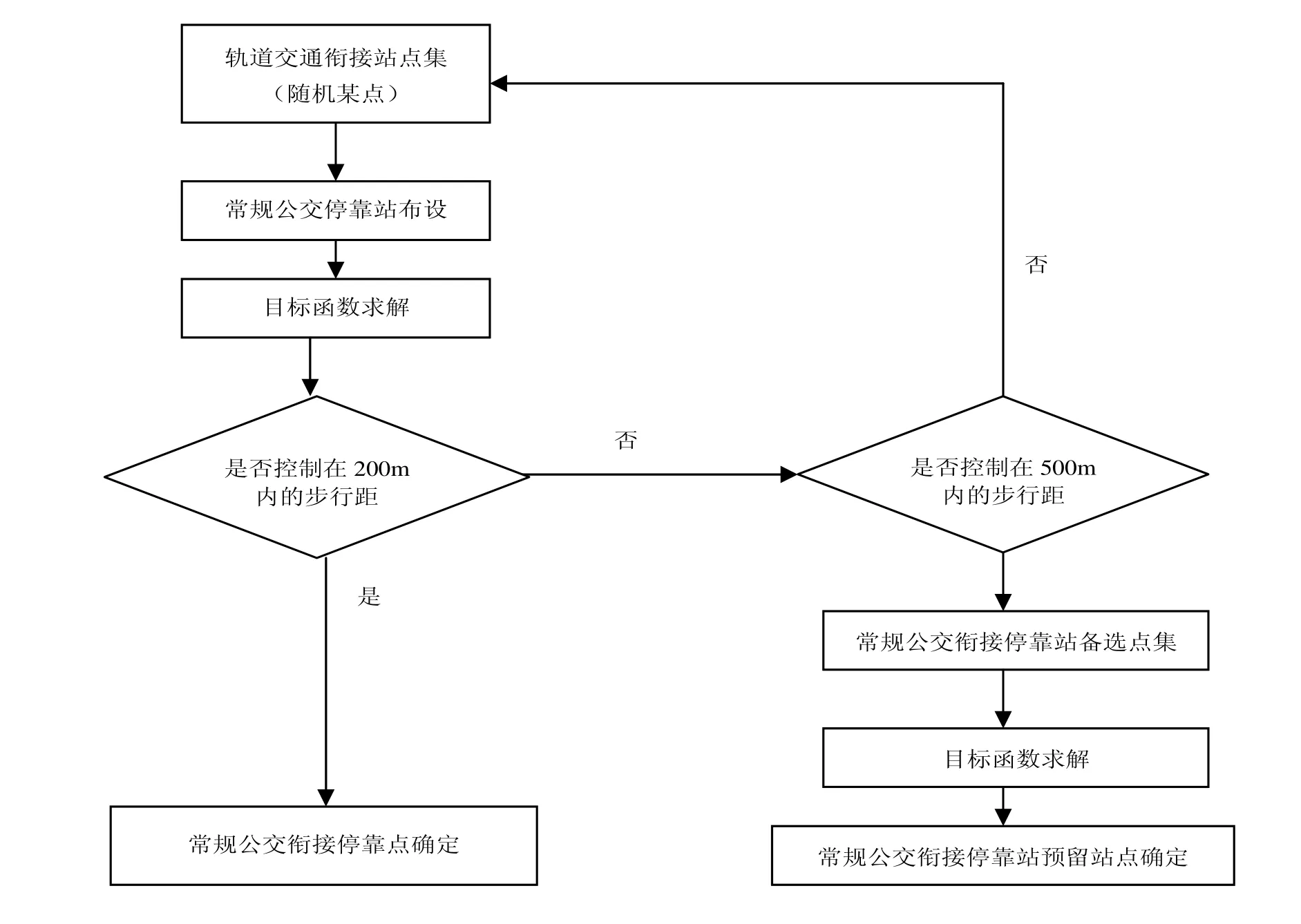
图1 基于换乘的常规公交站点的设计流程Fig.1 Design flow chart based on the conventional bus transfer station
4.2 交叉口处基于换乘的常规公交站点定位模型
目前城市轨道交通的出入口均处在人流量相对较大的交叉口附近,依据在轨道交通出入口附近设置常规公交站点的距离优先原则,在交叉口最常见的常规公交站点设置方式如图2阴影所示。
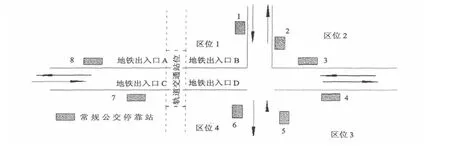
图2 交叉口处常规公交衔接站布局Fig.2 Connection layout of a conventional bus station at an intersection
已知条件:(1)定位模型的坐标原点设置在交叉口的中心点处;
(2)轨道交通各出入口坐标(Xj,Yj),
j∈ {A,B,C,D};
(3)停车线中心坐标( a14,b14),( a34,b34),( a23,b23),( a12,b12),(坐标下面的字母表示其所连接的区位,如14表示连接区位1和4);
未知求解:常规公交各衔接站点坐标( xi, yi),
i∈ { 1,2,3,… ,8 };
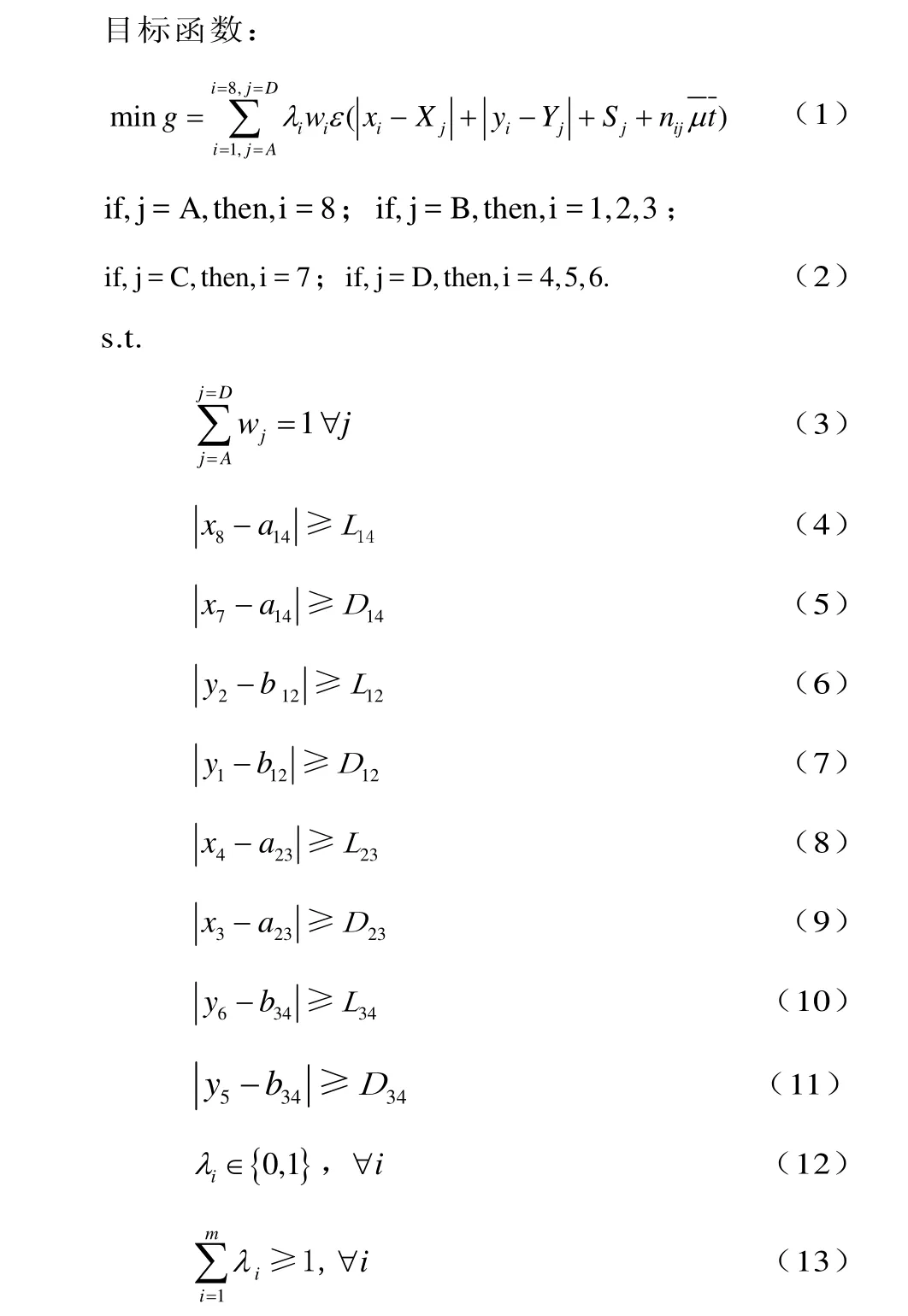
式中:j——轨道交通站点所对应的某个交叉口;
i
λ——第i个常规公交站点建设与否,1为建设,0为不建设;
wj——轨道交通某出入口的换乘客流占总换乘客流的比重;
ε——衔接调整系数;

L, D ——都为最大排队长度,L为在公交站排队的最大长度,D为在交叉口停车线排队的最大长度,二者计算公式均为:车辆平均到达率×平均车头时距×红灯时长[9];
nij——常规公交站i到j出口的过街次数;
μ——乘客平均步速,一般为3.5~4.5km/h;
t——换乘平均延误时间。
其中:式(1)为目标函数,求解在满足条件的情况下如何设置常规公交站才能使走行距离最短;式(2)权重和为 1;式(3)到式(10)是使常规公交站点的设置满足最大排队长度的要求;式(11)(12)表示常规公交站设置与否的变量,0为不设置,1为设置,且至少设置一处。
5 结 论
结果表明:
(1)既有公交站的优化对于换乘模型会产生一定的影响,通过对实地调查数据的标准化处理,得出影响的主要因素特征和比例,并采用主成分分析法求解出对应模型的调整系数。
(2)在交叉口处,行人的交通换乘行为受到轨道交通和常规公交吸引范围的影响,根据实际调研数据和相关文献资料,将步行间距分别控制在 200 m和500 m的区间内,确定出行人换乘所需的衔接停靠点和衔接预留停靠点的位置。
(3)建立了交叉口处基于换乘的常规公交站点定位模型,并给出了模型的具体求解方法。在满足最大排队长度的条件下,通过综合考虑过街次数、延误时间等和换乘选择的线性函数关系以及既有公交优化调整系数的影响,得到了行人走行距离最短的换乘方案。
[1] 隋晓波.城市轨道交通换乘站设施协调研究[D]. 北京:北京交通大学, 2008, 06.
[2] 彭其渊, 段力伟, 文超, 余晓珂. 突发大客流对轨道交通换乘站服务水平和列车运行影响分析[J].城市轨道交通研究, 2014, (2): 46-49
[3] 纪成亮. 浅谈轨道交通地铁换乘车站方案设计[J].城市建设理论研究, 2012,(11):210-214
[4] 何静. 铁路上海站南北广场换乘通道改建方案分析[J].中国铁路,2006(8):66-69
[5] 陈莎, 马林, 杨少辉. 北京轨道交通与其他交通方式的衔接研究[J]. 中国城市规划年会, 2008- 09-19.
[6] 杨晓光, 张海雷, 汪涛. 双港湾式公交停靠站的研究[J]. 公路交通科技,2007, (9): 104-108
