高速铁路声屏障在列车脉动风载荷下的强度计算

姚 澍 李人宪 康 健

西南交通大学，机械工程学院，成都 610031

0 引 言

高速列车运行速度的提高，会产生很大的噪声问题。而高速铁路线路大都要通过人口稠密、经济发达的地区，降低噪声已经成为高铁建设的一项重要课题。高速铁路声屏障是解决沿线噪声问题的有效措施之一[1-2]，并在国内外普通铁路以及高速铁路上有较广泛的应用。

声屏障一般距离轨道中心线3.65～4.8 m，由于距离较近，除了受到自然风载荷外，还受到列车通过时产生的脉动风载荷。德国科隆至法兰克福线路采用的声屏障就出现了损伤，影响到了行车安全以至于几乎全线拆除[3-4]。目前，对声屏障的研究主要集中在降噪以及声屏障顶部结构优化方面，对声屏障的结构强度和疲劳强度研究较少。在交变的气动力作用下，声屏障受到反复的冲击，有可能造成疲劳破坏，甚至影响行车安全。我国铁路声屏障的设计主要参考城市道路声屏障的规范，目前的结构设计以静力分析为基础，这是不够完善和科学的[5-6]。

列车通过时声屏障上的压力是怎么变化和分布的？在这个交变的气动力作用下，声屏障立柱的应力和变形是怎么变化的？立柱的应力和变形随列车速度又是怎么改变的？不同的声屏障距离气动载荷和结构应力如何变化？还有相当多的问题需要解决。本文采用计算流体力学仿真模拟列车通过声屏障的过程，采用流固耦合技术，将声屏障受到的气动压力较真实的加载为边界条件，利用有限元方法分析声屏障的受力情况，为声屏障疲劳寿命的估计提供一定的参考判据。

1 列车风的气动力特性计算

1.1 流场计算模型

本文采用CRH2车型，较细致的建立了头车、中间车和尾车组合的列车模型，长76.9 m。双线轨道，线间距5 m。路基及声屏障尺寸参考铁道部经济规划研究院发布的《路基声屏障通环8225、8325》[7]，列车轨道面高于声屏障基座0.9 m。声屏障不考虑列车进出边缘带来的影响，简化为高2.95 m的长直板。列车通过时车周围是一个三维、粘性、可压缩、非定常瞬态的流场，我们采用有限体积法对这一流场描述方程进行数值求解。图1为列车及声屏障的计算网格模型。

图1 计算模型的网格Fig.1 Gird of the computation model

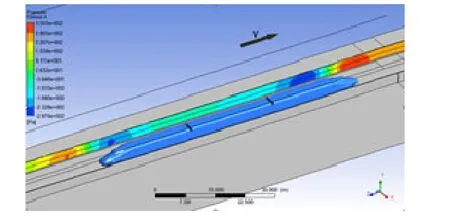
图2 列车在350km/h时声屏障上的压力云图Fig.2 Stress cloud chart on the noise barrier when train passes at a speed of 350km/h

1.2 声屏障上气动作用力计算

为分析不同工况下声屏障上气动载荷的变化，作者计算分析了三种声屏障距轨道中心距离（3.34，3.90，4.65 m）和三种列车行驶速度（350，400，450 km/h）的流场。图2为当车速350 km/h时某时刻声屏障面板靠近列车侧面的压力分布。此时，靠近列车头部的声屏障面板上形成了一个正压的“压力靶”和一个负压的“压力靶”[8]。压力靶的中心压力绝对值最大，向四周辐射状减小，列车中间声屏障区域的压力值较小。尾部与头部正好相反，先出现一个负压的“压力靶”，再出现一个正压的“压力靶”。随着时间的变化，压力靶位置也随着列车前进。

1.3 声屏障上气体压力变化规律

在声屏障内外两侧自下而上均匀取 8个测点测量列车经过时的压力，位置如图 3所示。列车以350 km/h的速度通过时，距轨道中心3.34 m（±0.05 m）声屏障上测点的压力变化如图4所示，各点的压力分布规律类似。压力表现为两个脉冲，车头靠近时压力骤升，至峰值后立即下降至负压的峰值。车尾接近时产生较大的负压，随即骤升至较大的正压峰值。随着列车远离，压力也下降的较快。

图3 测点位置示意Fig.3 Location of the observation points

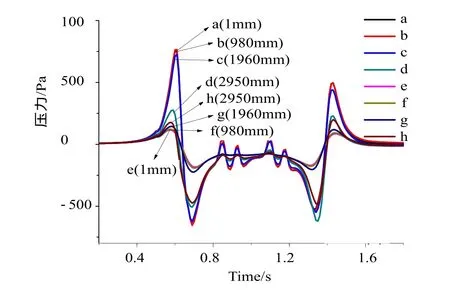
图4 车速为350km/h时测点的压力变化Fig.4 Pressure changes of the points when train passed at 350km/h

图 5是中心距 3.34 m的声屏障，在不同列车速度下测点的车头压力峰值。a—d点位于声屏障内侧面，压力自下而上变小，正压比负压的峰值变化剧烈。声屏障内侧面底部与顶部的正压相差64%左右，负压相差 22%左右。E—h点位于声屏障板的外侧面，压力自上而下减小。外侧面顶部与底部正压相差34%左右，负压相差61%左右。同一测点在不同速度下的压差最大能达到2 426 Pa，可见列车运行速度对声屏障上气动作用力的影响相当大。用a测点压力波的正负峰值差作为衡量指标，不同中心距气动力峰值差随车速变化如图6所示。

图5 不同速度下测点的压力峰值Fig.5 Peak pressures of the measuring points under different speeds

图6 不同中心距气动力峰值差随车速变化Fig.6 Aerodynamic force peak differences with the speed at different center distances

在声屏障同一高度上的压力变化，反映了随列车运动声屏障上气动力的变化。

声屏障受到的压力为一个随时间变化且不均匀分布的面载荷，如果用平均值或者最大值来代替这个分布的面载荷并不合理[9-10]。为模拟较真实的载荷条件，本文采用流固耦合技术将流场计算得到的面板压力加载到固体壁面上进行立柱的强度计算。

2 声屏障的强度分析

2.1 计算模型

根据铁路工程建设声屏障标准，金属插板式声屏障由 H型钢立柱和金属声屏障单元板构成。钢立柱间距为2 m，声屏障单元板安装在H型钢立柱之间，它们之间固定有单管橡胶垫。H型钢底部与底板有加劲板，并由底板固结地面[11]。图7为结构示意图。

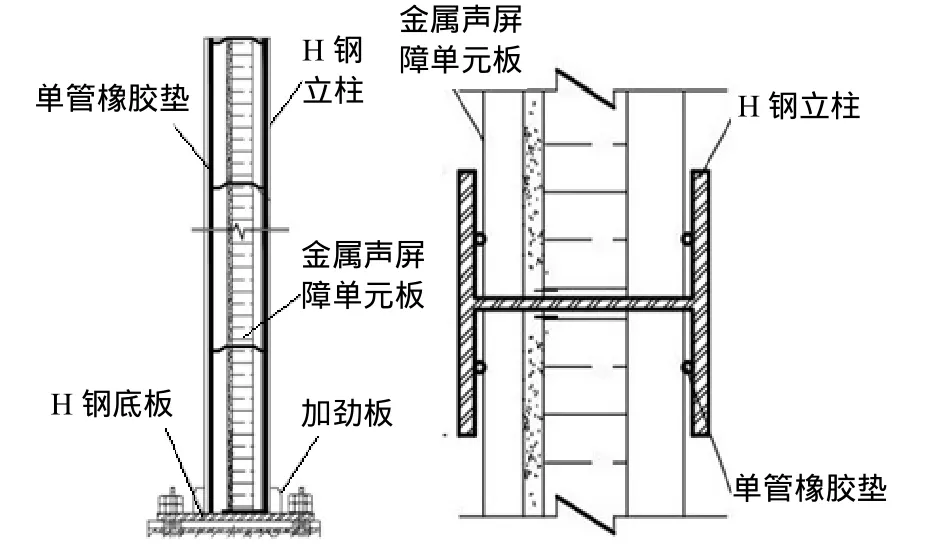
图7 金属插板式声屏障结构示意Fig.7 Structure of the metal noise barrier

根据通环标准，声屏障单元板最大挠度不超过L/100，结构变形在几厘米之间，结构变形对流场的影响可以忽略不计。利用流固耦合技术实现流场压力数据转换为固体计算的边界条件，在耦合面尽量使流场网格和固体网格尺度相接近。

气动力作用在声屏障单元板上，单元板通过橡胶垫施加力到立柱两侧的翼板上。本文将单管橡胶垫简化为只受压缩的弹簧单元。建立立柱和单元板受力计算模型，利用有限元法对中间的H钢立柱进行强度计算。

2.2 H钢立柱的受力规律

按上述模型，计算三种中心距(3.34，3.9，4.65 m)三种速度(350，400，450 km/h)九种工况。图8是中心距3.34 m，时速350 km/h时中间H钢立柱的变形和按照第四强度理论的等效应力在各个时间点的峰值，图8下方图为立柱最大变形随时间变化。每当列车经过一次，等效应力产生四个脉冲，其中第一个脉冲值最大。立柱的变形则反应了正负脉动列车风的影响，车头经过，立柱先向外侧倾斜，再向内侧移动。车尾经过则相反。不同中心距声屏障立柱最大等效应力随速度的变化如图9所示。最大等效应力随车速的增大而增大，随着声屏障距线路中心距增大而减小。同一距离声屏障上立柱最大应力随速度几乎是线性增加的，而斜率随距离的增大而减小。

图8 350km/h时H型钢出现的最大变形及应力Fig.8 The maximum deformation and stress of H-beam when train passed at 350km/h

图9 不同距离立柱随速度变化的最大等效应力Fig.9 Maximum equivalent stresses of columns at different distances with speed

为进一步分析立柱受力状况，分析加劲板顶端与H钢结合处四个节点位置的应力变化（图10）。图11为测点应力值，其中正应力方向为立柱高度方向y，切应力为底板平面xz方向。从图11可以看出，A、B点正应力变化趋势相同。车头通过时先产生正值应力脉冲，再变化为负值应力脉冲，车尾通过时则相反；C、D点正应力变化趋势相同，车头通过时先产生负值应力脉冲，再变化为正值应力脉冲，车尾通过时反向。A、B点车头通过时在y方向先受到拉伸后受压缩，C、D点y方向先受到压缩后受拉伸。说明车头通过时立柱先向远车侧弯曲，再反向弯曲。而车尾通过时则相反。

图10 测点位置Fig.10 Locations of the measuring points

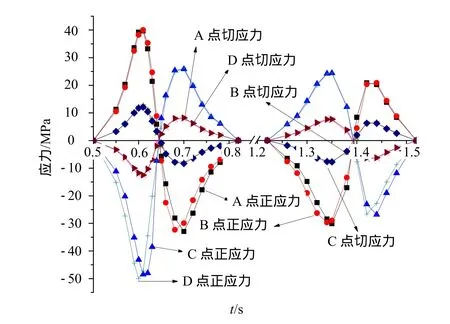
图11 测点应力变化Fig.11 Stress variation of the measuring points

切应力的存在说明立柱除受到弯曲变形外还受到扭转变形。切应力 A、D点变化趋势相同，B、C点变化趋势一致。A、D点切应力在车头通过时先负后正变化，B、C点切应力先正后负变化，说明立柱在车头通过时先向迎车头方向扭转，然后再向相反方向扭转，而车尾通过时扭转变化方向相反。

列车通过立柱产生弯扭组合变形，且弯矩扭矩各经历两次换向，使声屏障很可能产生疲劳破坏。

2.3 H钢立柱的疲劳分析

依据设计标准，声屏障要在一天经过210对列车条件下保证一定的使用寿命（立柱50 a）。根据上述计算，立柱受到的应力并不大，未达到材料的屈服极限，但有可能出现疲劳破坏。因此，下面依据疲劳强度理论估算声屏障立柱的疲劳寿命。依据上述强度计算，可获得危险点应力最大值的应力时间历程曲线，用雨流计数法进行统计分析，得到各个工况下的应力谱[12]。利用立柱钢材料的S-N曲线，运用 Goodman曲线进行平均应力的修正，得到表1的疲劳寿命预测。

表1中2.5E8是出现疲劳破坏的循环次数，按照疲劳理论对应无限寿命。表1的计算结果表明，该结构声屏障，在车速为350 km/h时，三种距离声屏障H钢立柱寿命均可实现超过50 a。车速为400 km/h时，中心距 3.34 m的立柱仅有 2.55 a。车速为 450 km/h时，中心距3.34 m处的立柱寿命减为0.63 a；中心距3.9 m的立柱寿命减为 1.06 a。可见除车速外，声屏障距离对其疲劳寿命也有非常大的影响。因此，车速在 400 km/h以上运行时，需要加强加劲板的高度和厚度，或者将声屏障安装至4.65 m的安全距离。

表1 各工况下的疲劳寿命Tab.1 The fatigue life under various working conditions

3 结 论

（1）列车经过时声屏障受到的压力为一个随时间变化且不均匀分布的面载荷。任意点压力随时间呈两个脉冲状变化。声屏障沿高度方向，内侧面压力自下而上变小，外侧面压力自上而下减小。声屏障上相同高度点上压力随列车运行速度向前变化。

（2）H钢立柱受到弯扭组合变形，弯矩扭矩各经历两次换向。车头通过时立柱先向远车侧弯曲，再反向弯曲，而车尾通过时则相反。同时，车头通过时先向迎车头方向扭转，然后再向相反方向扭转，而车尾通过时扭转变化方向相反。（3）每当列车经过一次，等效应力产生四个脉冲，其中第一个脉冲值最大。等效应力随车速的增大而增大，随着声屏障距线路中心距增大而减小。同一距离声屏障上立柱最大应力随速度几乎是线性增加的。

（4）H钢立柱受到的应力不大，可能出现疲劳破坏，车速和声屏障距离对其疲劳寿命也有非常大的影响。

[1] 赵丽滨，龙丽平. 列车风致脉动力下声屏障的动力学性能[J]. 北京航空航天大学学报，2009，35(4):505-508.

[2] 焦长洲，高 波，王广地. 声屏障结构的列车脉动风致振动分析[J]．西南交通大学学报，2007，42(5):531-536.

[3] 罗 锟，雷晓燕. 铁路声屏障降噪效果影响因素分析[J]．噪声与振动控制，2008，142(5): 142-146.

[4] 房 建，雷晓燕. 高速列车环境噪声评价标准及应用[J]. 交通运输工程与信息学报, 2007, 3: 50-56.

[5] 李晏良，李耀增，辜小安 等. 高速铁路声屏障结构气动力测试方法初探[J]．铁道劳动安全卫生与环保，2009，36(1): 22-26.

[6] 戚振宕，李人宪. 高速铁路声屏障气动特性仿真分析[J]．路基工程，2011,（4）：9-12.

[7] 吕坚品，张继文 等. 既有铁路桥梁声屏障的高速列车脉动风致相应[J]. 西南交通大学学报，2009,44(4): 548-551.

[8] 颜 坚，王乾锁 等. 高速铁路插板式声屏障抗弯能力有限元分析[J]．环境工程，2012，4(30): 75-78.

[9] 朱正清，成志强. 高速铁路声屏障气动力的数值模拟研究与试验验证[J]．铁道标准设计，2011 10:77-80.

[10] 陈向东，李树德等. 基于ALE的高速列车声屏障脉动力数值模拟研究[J]．铁道学报，2011，（12）：21-26.

[11] 通环(2009)8225/8325. 铁路工程建设通用参考图时速350km客运专线铁路路基插板式金属声屏障[S].

[12] 李舜酩. 机械疲劳与可靠性设计[M]. 北京：科学出版社，2006.