不同类型城市轨道交通车站站台客流特性对比研究

孙小菲 陈旭梅 王佑安

北京交通大学，交通运输学院，北京100044

0 引 言

乘客是城市轨道交通系统中最复杂最灵活的因素，客流特性的研究对提高轨道交通车站服务效率至关重要，因此，城市轨道交通客流特性研究备受国内外学者关注。早在 20世纪 50年代末，Hankin和Wright[1]就调查了伦敦地铁通道的行人交通流，建立了单方向行人流的速度、密度和流量之间的关系。随后，Fruin[2]、Harris[3]、Daly[4]分别研究了不同交通设施内的行人交通特性。国内的专家和学者也开展了一系列的研究工作。许婷[5]提炼出“环境-心理-行为”的微观分析模式，并对行人个体和行人流的行为从形成机理角度进行了分类研究。邹晓磊[6]构建了城市轨道交通车站乘客群体行为研究框架，进一步建立了群体行为模型，形成了乘客群体各层次行为描述的完整体系。常丹[7]、张晓军[8]、杨涵[9]等对轨道交通车站内客流特性进行了宏观和微观层次的建模研究。

行人行为的复杂多样性、灵活性和随机性为研究工作带来了一定难度，使得既有研究存在角度不全面等问题。城市轨道交通车站内的行人交通行为受到其所在环境的影响，所以，对乘客行为特性的分析需要考虑到城市轨道交通车站的特点。本文以乘客为出发点，围绕不同类型城市轨道交通车站站台客流特性对比这一研究目标，根据车站地理位置和其主要功能将城市轨道交通车站进行分类（分为换乘站、首末站和中间站），从微观和宏观两个层次进行研究，即乘客个体行为特性分析和乘客群体行为特性分析，从而提高乘客乘降效率，减少安全事故发生率。

1 不同类型城市轨道交通车站站台乘客个体行为特性分析与建模

速度是反映行人交通特性的重要指标之一，受到步幅和步频的影响。步幅是指乘客行走时每跨出一步，两脚脚跟与脚跟或脚尖与脚尖的距离。步频是指乘客行走的频率，即乘客行走时单位时间内跨步的次数。速度等于步幅和步频的乘积。每个人具有习惯步幅、步频，整体表现为个人的习惯行走速度[10]。故在此重点对乘客行走速度、步幅和步频进行研究。

考虑到北京地铁1号线和2号线使用时间长，客流稳定，本文选取首末站苹果园站（侧式站台）、换乘站复兴门站（岛式站台）和中间站长椿街站（岛式站台）三个车站，采取视频观测加以人工辅助的方法进行实地调研，以三个车站下午平峰（13:00~15:00）和晚高峰（17:00～19:00）实测数据为依据。其中，在每个车站取40人为样本，对城市轨道交通车站站台的男女乘客速度（m/s）、步幅（m）和步频（步/s）特性进行分析，进而建立反映城市轨道交通乘客速度、步幅和步频特性间关系的数学模型。

1.1 不同类型城市轨道交通车站站台乘客个体行为建模

对调研得到的数据进行处理分析得到平峰和高峰时期三个车站站台男女乘客的步频-步速和步幅-步速图及模型。以苹果园站男性乘客为例进行说明，如图1所示。

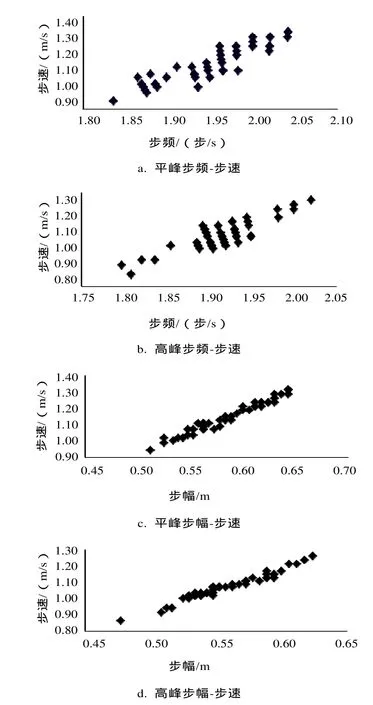
图1 苹果园站男乘客步频-步速、步幅-步速关系Fig.1 Relationships among stride, velocity and stride frequency of male passengers at Pingguoyuan station platform

图 1表明，苹果园车站站台平峰男乘客步频越大，速度越大，步速与步频基本呈正线性关系。同理，乘客步速随步幅的增大而增大，且步幅和速度基本呈线性关系。

分别以步频、步幅为自变量，建立模型：

模型中，1b、2b分别表示速度v对步频stepf、步幅paced的敏感程度，即1b或2b越大，速度对步频或步幅的敏感程度越高，1a、2a为常数。

利用SPSS软件进行线性回归，计算相关系数，通过统计分析发现其他车站男女乘客步频-步速、步幅-步速呈现同样规律，故用相同方法进行建模。

1.2 不同类型城市轨道交通车站站台乘客个体行为模型对比分析

通过SPSS线性拟合得到不同类型城市轨道交通车站站台乘客个体行为模型的参数，如表1所示。

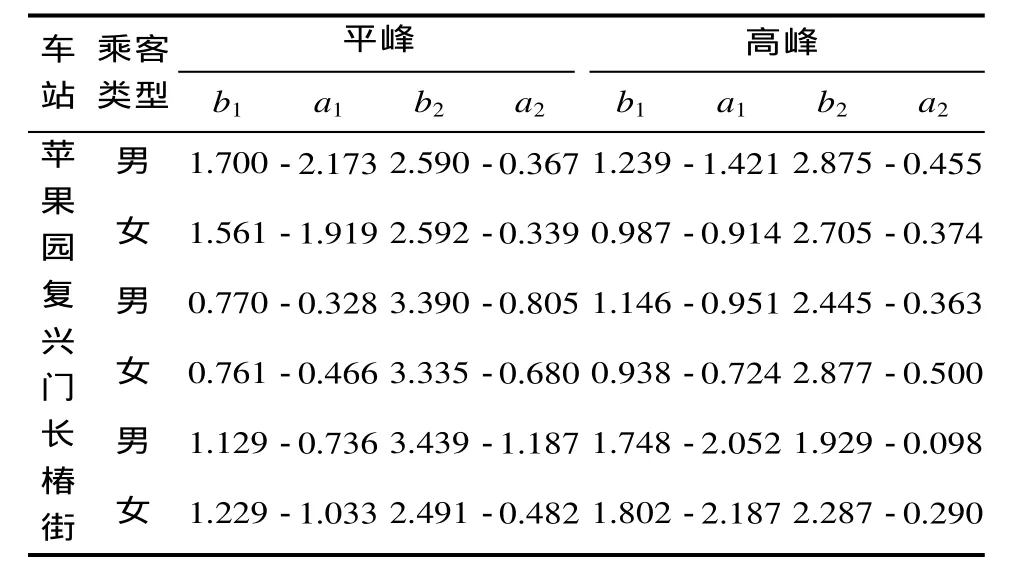
表1 不同类型车站站台乘客个体行为模型参数Tab.1 Models parameters of individual behavior on platforms of different stations

总体来看，步速对步幅比步速对步频的敏感程度高。长椿街车站站台男女乘客步速对步频的平均敏感程度最高，平均1b为1.477，复兴门车站站台男女乘客步速对步幅的平均敏感程度最高，平均2b为3.012。这是由于换乘站复兴门站客流复杂，流量相对较大，站台密度较大，故乘客步幅对步速影响大。而长椿街站作为中间站，站台宽度较苹果园宽，且客流量相对较小，乘客可保持正常步幅，所以乘客步速更多取决于步频。

2 不同类型城市轨道交通车站站台乘客群体行为特性分析与建模

车站作为城市轨道交通网络中的节点，大量乘客在此集散。当列车到达车站时，站台出入口处会出现脉冲式的局部客流拥挤现象，如果出站客流得不到及时疏散，将导致地铁站台拥堵，降低地铁车站运营效率，甚至成为安全隐患。出站客流特性研究对客流组织工作至关重要。同时，站台上乘客分布和流线分布受乘客对候车区选择特性的影响，根据乘客对候车区的选择特性设置站台设施将利于提高站台服务效率。因此，从群体角度研究站台出站客流密度与行进速度的关系以及乘客对候车区选择特性，对分析地铁站台疏散能力、提高地铁服务水平和乘客安全具有重要意义。

2.1 不同类型城市轨道交通车站站台客流速度-密度分析及建模

2.1.1 不同类型城市轨道交通车站站台客流速度-密度分析

通常，人流拥挤程度直接影响行进速度。人流密度越大，行人之间的间隙越小，行人行进越缓慢；反之，人流密度越小，行人行进越迅速。目前，国外对拥挤状态下的人员移动速度与人流密度的研究已经积累了大量的观测数据，通过将人流密度和速度进行拟合，获得了线性关系、对数关系、指数关系、三角函数关系等。我国陆君安、方正等专家根据交通动力学理论，建立了行人行进速度关系模型[11]。

仍然选取以上三个车站，并针对临近出站楼梯区域进行实地调研，苹果园车站选取出站楼梯附近长4.5 m、面积为 11.48 m2的区域；复兴门车站选取临近站台东部楼梯长4 m、面积为9.6 m2的区域；长椿街车站则是选取临近站台东部楼梯长 3.6 m、面积为11.52 m2的区域。利用调研得到的数据绘制各车站平峰和高峰速度-密度图，如图2所示。

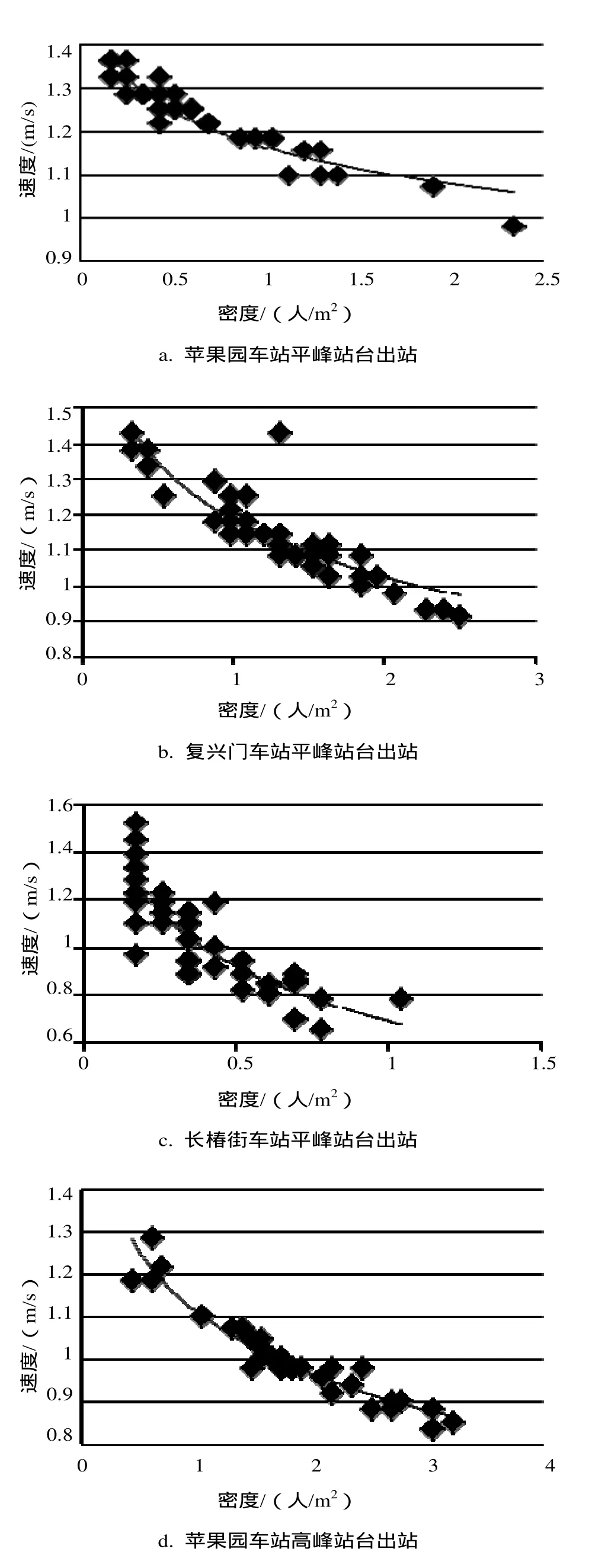
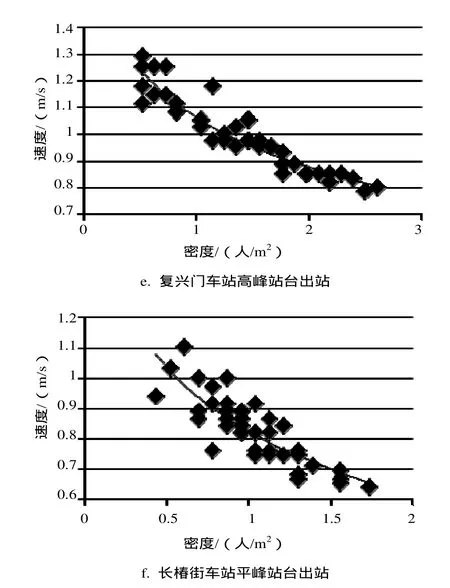
图2 各车站平峰和高峰速度-密度图Fig. 2 Relationship between speed and density at the peak hours and off-peak hours of each station

用统计软件SPSS对观测数据进行处理和分析，结果表明，对数关系能较好地表达密度和行走速度之间的关系，关系式如下：

式中，ρ为人流密度；v为人流速度；E、F为常数。

通过实地调研，发现三个车站站台出站客流呈脉冲式，随着列车的到来，客流短时间内聚集。三个车站在平峰时期，客流速度较大，密度较小；在高峰时期，客流量较大，出站客流速度随密度的增大而减小。平峰时期，换乘站复兴门站客流量较大，出站客流密度较大。高峰时期，由于苹果园站为侧式站台，站台宽度小，出站乘客大量集聚，密度较大。

2.1.2 不同类型城市轨道交通车站站台出站客流速度-密度模型对比分析

通过SPSS软件对数据进行拟合分析，得到三个车站出站乘客密度-速度关系模型（见表2）。

表2 不同类型城市轨道交通车站站台客流速度-密度模型Tab.2 Relationship models between passengers’ speed and density at different stations

模型v(p) =Eln(ρ)+F中的常数E可以表示速度受密度影响程度的大小。从标定的模型可以看出，无论平峰还是高峰，长椿街车站的站台出站乘客速度最易受密度影响，其平峰时期和高峰时期E的绝对值分别为 0.332和 0.306；复兴门车站次之，其平峰时期和高峰时期E的绝对值分别为0.231和0.268；苹果园车站最小，其平峰时期和高峰时期E的绝对值分别为 0.124和 0.209。随着密度的增大，长椿街车站站台出站乘客的速度下降最快。这是因为长椿街车站站台作为中间站，站台宽度比复兴门车站小，一旦密度变大，出站乘客速度要比复兴门车站乘客出站速度下降得快；而且复兴门车站和长椿街车站均为岛式站台，存在进站方向客流和站台上徘徊的客流的干扰，苹果园车站是首末站且为侧式站台，乘客出站站台上仅有一个方向的客流，没有其他方向客流的干扰，所以，长椿街车站站台乘客速度最易受密度影响。

2.2 不同类型城市轨道交通车站模型标定与分析

以下采用的模型借鉴李灿[12]建立的模型，并在其基础上引入候车区最大容纳人数加以改进。该模型依据交通流分配中的用户均衡原理和Beckmann交通平衡分配模型建立候车区乘客平衡分配模型。首先，对模型条件进行说明：

（1）若站台的设计形式为岛式，站台内会有两个不同方向的候车乘客。本模型中只考虑一个方向的候车乘客，模型中提到的候车乘客和候车区都是指在同一方向上的。

（2）假设进入站台的乘客是随机到达的。

（3）假定进入站台的乘客对候车区的选择明确，本模型中不考虑乘客会处于徘徊状态的情况，认为乘客进入站台后直接进行候车区。

（4）在进行新一个候车周期的乘客分配时，模型假定各候车区初始的候车乘客人数为零。

对模型中所用到的参数和变量说明如下：

aj—— 候车周期内j入口到达的乘客量；

ci—— i候车区最多能容纳的人数；

xi—— i候车区的候车人数， xi≤ ci；

lij—— i候车区到j进口的走行距离，单位为m；

Fij—— i候车区对从第j入口进入站台的乘客的吸引度；

Fi—— 候车区i的吸引度；

uj—— 各候车区对j进口乘客吸引度的最大值；

其次，从影响乘客候车区选择行为的因素出发对候车区选择行为进行分析。

（1）候车区阻扰度

阻扰度表示了各候车对某一入口进入乘客的“排斥”，这种“排斥”是由车站的物理布局确定的，它与是否存在乘客无关，也就是候车区具有特定的客观不变特性。在乘客整个选择过程中，候车区对乘客产生的阻扰度始终保持不变。

（2）候车区面积

乘客在进行候车区选择时会考虑候车区面积，该因素决定候车区能够容纳的人数，候车面积直接影响乘客候车的舒适度。

（3）候车区可用面积

对于候车区来说，容纳不同的人数时，对乘客的吸引度不同，候车区的可用面积直接影响乘客上车的难易程度。因此，候车区可用面积也是必须考虑的因素之一，可由候车区还能容纳的人数表示。

（4）候车区距入口距离

候车区距入口距离也是乘客在进行候车区选择时考虑的主要因素，直接决定乘客在站台的走行距离。一般而言，若其他条件相同，乘客更愿意选择距自身所在进口近的候车区。

通过上述分析，将各影响因素代入模型，建立乘客候车区选择模型如下：

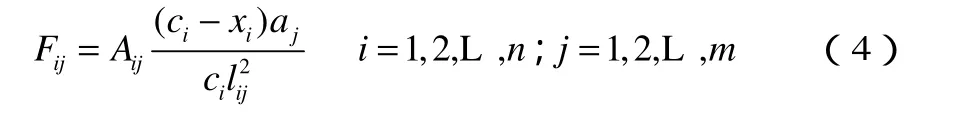
该模型的约束条件如下：

首先，平衡分配过程中应该满足交通流守恒的条件，即各候车区内的乘客之和等于各进口的乘客总量。其次，候车区的总吸引度是候车区对各个进口的吸引度的累加。最后，候车区的候车人数应满足非负约束。上述定义的变量和参数用公式表示如下：

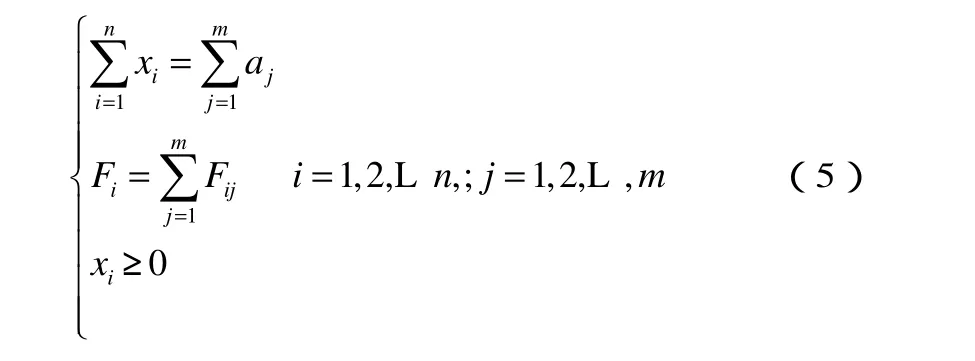
基于模型的参数设定和上述约束条件，用求解目标函数极大值的方法来求解候车乘客分配问题，构建候车区乘客平衡分配模型如下：

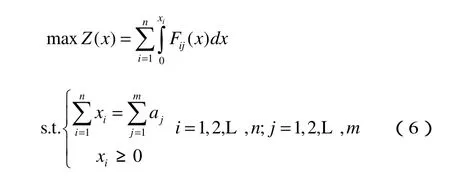
由平衡分配模型知，大量的乘客选择最终形成了最后的平衡状态，由此可以得出，在未到达平衡状态前，候车区对乘客的吸引总是不平衡的，乘客选择某个候车区，也就使该候车区逐渐向平衡状态接近。当候车区乘客交通分配达到平衡时，若有xi＞ 0 ，必有Fij=uj，同时有u1=u2= K =um，说明如果i候车区内有乘客候车，那么该候车区对所有进口的吸引度相等；同时，若有xi= 0 ，必有Fij＜uj，说明如果i候车区内没有乘客候车，那么该候车区的吸引度一定小于有乘客候车的候车区的吸引度。

应用模型首先对模型待定参数Aij进行标定。Aij表示候车区i对某入口j进入的乘客的“排斥”，Aij值越大，也就说明i候车区对j进口进入的乘客越“排斥”。平峰时段客流量较少，难以达到平衡状态，故选用晚高峰时段的调查数据。苹果园站和复兴门站站台为南北走向，自南向北依次对24个候车区进行编号，长椿街站站台为东西走向，自东向西依次对候车区进行编号，如图3所示。测量每个候车区面积、各入口到各候车区距离。对乘客候车区选择行为观测11次，取前 10次数据进行模型标定（令u1=u2= K =um=1，代入ci、xi、aj、lij，标定各候车区Aij，标定结果如表 3所示），第 11次数据进行模型验证，验证结果表明三个车站各候车区人数平均误差绝对值为1.28人/候车区，误差较小，证明标定的模型能较真实的反映乘客候车区的选择情况。

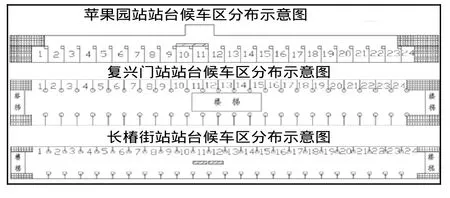
图3 三个车站站台候车区分布示意Fig.3 Layouts of the waiting areas of three station platforms

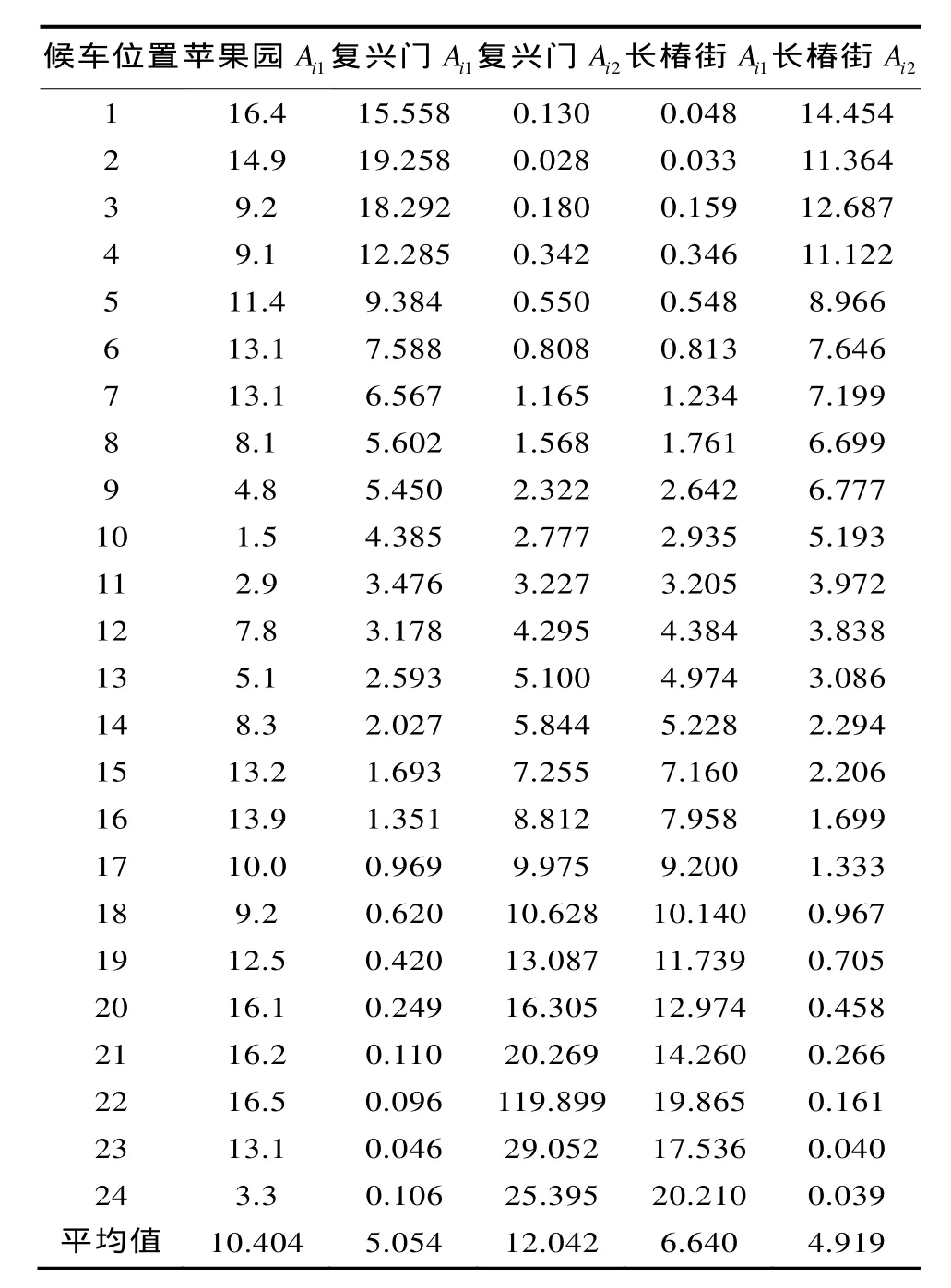
表3 不同类型城市轨道交通车站 ijATab.3 ijAof different urban rail transit stations

通过建模分析可以看出，同一车站乘客对不同位置候车区选择不同，不同类型车站的乘客对同一位置候车区的选择也不同。乘客对候车区的选择主要基于到达候车区的便捷程度、候车区面积以及该候车区已有人数。候车人数平均值在不同类型车站站台上的分布如图4。苹果园车站乘客更倾向选择距进口近且面积大的候车区，因为苹果园车站是首末站，每一辆到站的车辆均为空车，所以乘客不愿意也没必要往站台两端走去寻找候车乘客少的候车区。虽然候车区10和11是离站台进口最近的两个候车区，但是这两个候车区候车面积相对其相邻候车区面积较小，而且，在调研过程中发现，候车区10和11处有防护栏，导致乘客必须绕过防护栏才能到达候车区，并不方便，所以，乘客倾向选择方便到达、空间大的候车区。复兴门车站乘客更愿意选择距离入口近的候车区，复兴门车站作为换乘车站，换乘客流较大，1号线换乘2号线距离较长，乘客经过换乘，不愿意选择距离入口远的候车区。长椿街车站乘客除了同样倾向选择距离入口近的候车区外，对候车区已有人数也很敏感，这是因为长椿街车站是中间站，进站乘客从进站口到站台走行距离不长，而且乘客考虑到车上已有乘客，会根据候车区已有人数来预测自己上车难度，综合考虑进行候车区的选择。

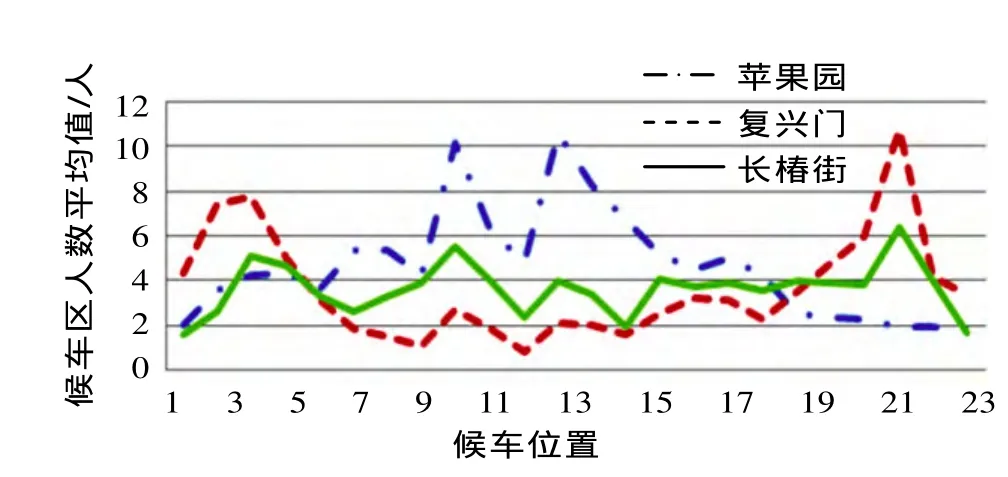
图4 三个车站各候车区平均人数对比图Fig.4 Comparison among the mean people numbers in the waiting area of the three stations

3 结 论

本文基于客流特性调查数据，从乘客个体行为特性和群体行为特性两大方面出发，通过建立数学模型，对三个不同类型车站站台的客流特性及模型进行了对比分析，主要得到以下结论：（1）不同类型城市轨道交通车站频-步速、步幅-步速呈现线性关系；（2）中间站长椿街车站站台乘客速度最易受密度影响，这与车站类型、站台形式有关；（3）文中建立的乘客候车区选择模型能较好地描述乘客候车区选择行为；（4）乘客对候车区的选择主要基于到达候车区便捷程度、候车区面积以及该候车区已有人数。本文仅限于车站站台上乘客行为特性的研究，不同类型城市轨道交通车站通道、楼梯及自动扶梯等其他设施处乘客行为特性有待进一步研究。

[1] Hankin B.D. Wright R.A．Passenger flow in subways[J]．OR(Operational Research Quarterly)．1958, 81-88．

[2] Fruin J. Pedestrian planning and design[M]. New York: Metropolitan Association of Urban Designers and Environmental Planners Inc，1971．

[3] Harri N G．Capacity restraint simulation in a public transport environment[J]. London：Traffic Engineer and Control, 1989, 30(6)：312-315．

[4] Daly P. N., McGrath, Annesley. Pedestrian speed/flow relationships for underground station[J]. Traffic Engineer and Control, 1991, 32(2):75-78.

[5] 许婷. 城市轨道交通枢纽行人微观行为机理及组织方案研究[D]. 北京：北京交通大学，2007年.

[6] 邹晓磊.城市轨道交通车站乘客行为及客流组织研究[D]. 上海：同济大学，2009年.

[7] 常丹，地铁行人微观行为参数量化研究[D]. 北京：北京交通大学，2010年.

[8] 张晓军，张宁，陈晖. 城市轨道交通行人通道路阻函数拟合[J]. 城市轨道交通研究，2011，14（1）：33-37.

[9] 杨涵，伍梦欢，张含笑，刘智丽. 地铁换乘站不同设施区域乘客走行速度分析[J]. 交通运输系统工程与信息，2011，11（增1）：141-146.

[10] 史建港. 大型活动行人交通特性研究[D]. 北京：北京工业大学，2007年.

[11] 李三兵. 城市轨道交通车站客流特征与服务设施的关系研究[D]. 北京：北京交通大学，2009年.

[12] 李灿.城市轨道交通枢纽乘客流交通特性分析及建模[D]. 北京：北京交通大学，2008年.