基于OC-Seislet变换的海洋涌浪噪声衰减方法
2015-03-11勾福岩
勾福岩,刘 财,刘 洋,王 博,2,冯 晅
1.吉林大学地球探测科学与技术学院,长春 130026 2.石家庄经济学院勘查技术与工程学院,石家庄 050031
基于OC-Seislet变换的海洋涌浪噪声衰减方法
勾福岩1,刘 财1,刘 洋1,王 博1,2,冯 晅1
1.吉林大学地球探测科学与技术学院,长春 130026 2.石家庄经济学院勘查技术与工程学院,石家庄 050031
在海上地震资料采集过程中,涌浪噪声是一种常见的噪声干扰,这类噪声一般表现为低频、强能量、长周期,使用一般的方法很难在去噪的同时达到信号保真的效果。笔者针对该噪声的特征,选取了基于波动方程炮检距连续(offset continuation,OC)算子的OC-Seislet变换方法进行消噪处理;该方法应用OC算子来表征复杂波场,对含噪声数据进行压缩,在变换域通过软阈值处理实现信噪分离,再将结果反变换到数据域,从而达到去除涌浪噪声的目的。通过对模型数据和实际数据的处理,验证了OC-Seislet变换方法能够在去除原始数据中涌浪噪声的同时,最大程度地保护复杂构造下的地震波信息。
炮检距连续算子;OC-Seislet变换;涌浪噪声;软阈值
0 引言
海上拖缆在采集数据时,受海流的干扰,电缆在垂向上起伏抖动,从而使采集到的数据在地震剖面上出现垂直条带状分布的涌浪噪声。涌浪噪声是海洋地震资料中常见的噪声类型,特别是拖缆较浅时,噪声更强烈。涌浪噪声具有高振幅、低频率、窄频带的特点,在地震记录上,整体背景噪声显得特别明显。由于其衰减很慢,所以在单炮记录上噪声的振幅几乎不随时间衰减,使得后期资料处理较为困难。Hassan等[1]应用经验模式分解(EMD)方法直接去除低频涌浪噪声,但是对于振幅和频率变化较大的涌浪噪声,该方法有时容易产生频率混叠。陈见伟[2]采用区域振幅衰减技术压制涌浪噪声,具有很好的相对幅值保持特征,但是对深层噪声密集区域的处理效果有时不是很理想。宋家文等[3]在EM(expectation maximization)算法的基础上,提出了地震道随机重排联合EM算法的涌浪噪声衰减方法,该方法对密集分布的高振幅涌浪噪声压制效果很好,但是有时会损伤振幅较强的有效信号。徐善辉[4]和周伟等[5]将HHT(Hilbert-Huang变换)方法应用到海上资料分析中,可以有效地衰减低频、高振幅的涌浪噪声。牛华伟等[6]应用分频振幅衰减法,通过求取给定频率段不同时窗内地震样点的振幅强度,预测出强能量的涌浪噪声,能够改善地震资料的信噪比。Bekara[7]提出了一种数据驱动的方法来去除涌浪噪声,该方法可以使用相同的参数对不同噪声级的地震道进行处理,有很强的适应性,减少了测试工作量,但是与传统方法相比,该方法去除涌浪噪声的效果没有明显的改善。Hu等[8]针对强能量、低频率的叠前地震资料,提出了傅里叶域低频滤波级联的方法,该方法根据反射信号和噪声之间的不同视波速来实现信噪分离,可以有效地压制涌浪噪声,保护信号。
稀疏变换在科学和工程的去噪问题上有着广泛的应用。在地震数据处理领域,巩向博等[9]提出压制噪声的高分辨率Radon变换法,能有效地压制规则干扰和随机噪声,并且计算效率很高。王德利等[10]应用curvelet稀疏变换阈值迭代法去噪,充分利用了curvelet变换对地震数据表示的稀疏性,将去噪问题转化为基于curvelet稀疏变换的L1范数最优化问题,该方法不仅能够获得较高的信噪比,而且对有效信号的损失较小。李海山等[11]采用形态分量分析(MCA)方法去除地震数据中的随机噪声,在时间和空间上都具有很强的噪声压制能力,并且对有效信息损害较小。刘琼等[12]提出的基于小波域稀疏性的地震数据去噪方法,通过求解一个L1范数最优化问题来估计不含噪的小波系数,从而实现对地震数据的去噪,对于低信噪比的数据去噪效果较好。徐明华等[13]提出的基于压缩感知理论的缺失地震数据重构方法中,应用一种新的自适应阈值迭代算法,可以很好地消除稀疏系数中的随机噪声干扰。这些方法在去除一般噪声时都能够得到较好的效果,但是对于低频强能量的涌浪噪声的压制效果往往不是很理想。
2006年,Fomel[14]开发了一种针对地震数据方向性的数学变换方法----Seislet变换,该方法针对地震数据进行特殊设计,具有高压缩性;但是早期的Seislet变换并不能为地震数据提供最佳的稀疏表示。Liu等[15]在此基础上,根据波动方程的动力学关系,通过结合动力学炮检距连续(offset continuation, OC)算子[16],开发了一种表征复杂地震数据的稀疏变换方法,即OC-Seislet变换。该方法为地震数据提供了最佳的压缩效果,能够有效地解决地震波场的二维噪声压制及波场重建问题。
笔者在已有研究的基础上,将OC-Seislet变换应用到涌浪噪声衰减的问题中,利用最佳化变换基函数压缩含有涌浪噪声地震数据中的有效波场信息,在变换域内选取适当的阈值参数做阈值处理,结果再反变换到数据域,最终实现对地震数据中涌浪噪声的有效压制。
1 理论基础
1.1 Seislet变换
Seislet变换是一种利用地震数据模式特征压缩数据的稀疏变换方法;以小波提升算法[17-18]为基础,与地震数据模式识别相结合,使用不同的模式对地震数据进行预测,能够得到不同类型的Seislet变换。例如,通过平面波分解(plane-wave destruction,PWD)滤波器获取地震同相轴倾角模式[19],沿着地震倾角方向表征地震数据特征,可以得到基本的PWD-Seislet变换的定义[20],其核心基于平面波重构与地震倾角的关系[21]。
提升算法的核心是更新算法和预测算法,通过预测算子得到高频信息,通过更新算子得到低频信息。提升算法中正变换的步骤如下:
1)将数据分解为奇数序列o和偶数序列e。
2)计算奇数序列与偶数序列预测值之间残差r以及数据的近似值c:

(1)
其中:P是预测算子;U是更新算子。
3)近似值c成为新的数据,重复以上步骤得到下一级数的变换系数。
对小波提升方案中离散小波变换的预测算子和更新算子进行修改,以CDF 5/3双正交小波结构为例,我们可以得到PWD-Seislet变换中对应的预测算子P和更新算子U:
(2)
(3)

通过正向Seislet变换,地震数据转变到稀疏域。在稀疏域内有效信号被压缩在很小的动态级数范围内,而噪声却不能被预测和压缩;即有效信号的能量在变换域内主要集中在很少的几个系数中,而噪声的能量却分布于整个变换域内,所以信号对应的变换系数要远大于噪声对应的变换系数。接下来,选取适当的软阈值参数:认为大于该阈值参数的变换系数,主要是由信号引起的,反之则认为是噪声引起的。这样,对变换域内系数做软阈值处理后,再反变换回数据域,就达到了去噪的目的。Seislet变换阈值去噪流程如图1所示。

图1 Seislet变换去噪流程示意图Fig.1 Workflow of seislet transform denoising
PWD-Seislet变换可以提供比经典小波变换更加有效的地震数据压缩能力,但是该变换的倾角受强噪影响较大,精度不高,对于含涌浪噪声的地震数据,难以得到合理的稀疏域。而OC-Seislet变换从地震波动力学角度分析地震数据,不容易受强噪影响,并且海上勘探地下构造往往比较复杂,OC-Seislet变换可以更好地压缩复杂地震波场。所以笔者选取OC-Seislet变换对含涌浪噪声的海上地震数据进行去噪处理。
1.2 OC-Seislet变换
OC-Seislet变换是Seislet变换类的一种方法,其数据模式为炮检距连续下的动力学方程,通过结合炮检距连续算子进行预测运算。同样以CDF 5/3双正交小波为例,我们可以得到OC-Seislet变换的更新算子和预测算子:
(4)
(5)
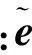
在Fomel[16]的炮检距连续微分理论中,OC偏微分方程有如下形式:
(6)
其中:U(x,h,tn)是地震数据;x、h、tn分别为中心点坐标、炮检距坐标以及NMO(正常时差校正)后的时间轴;n为该时间轴上的采样点。对时间轴做拉伸变换,然后沿拉伸后的时间轴和中心点坐标轴对数据体做二维傅里叶变换,可以对公式(6)进行求解,得到的方程解有以下形式:
(7)

(8)
其中,Γ是伽马函数。
在高频渐进下,方程(6)的解有如下形式:
(9)
其中:
(10)
(11)
则可得到OC算子的形式为
(12)
其中,i是炮检距坐标轴上的采样点。
构建OC算子时,需要对数据作动校正处理。常规的速度分析方法尽管能够在一定程度上抵抗随机噪声的干扰,但对于涌浪噪声的强振幅往往效果较差。Fomel[22]提出一种AB系数相似方法,该方法能够更好地分析强随机噪声(如涌浪噪声)条件下的叠加速度,本次研究使用该方法为OC-Seislet变换提供较为准确的动校正数据。
2 模型测试
为了测试OC-Seislet变换对地震数据中涌浪噪声的压制效果,首先建立一个模型进行验证。笔者选取标准French模型的二维切片(图2),通过克希霍夫正演建立一个时间(t)-共中心点(x)-炮检距域二维叠前数据体(图3),三个剖面分别选取:0.6 s的时间切片(图3a)、0.216 km的共炮检距切片(图3b)以及0.72 km的共中心点切片(图3c)。

图2 标准French模型的二维切片Fig.2 2D slice out of the benchmark French model

图3 时间-共中心点-炮检距域内的二维叠前数据模型Fig.3 2D synthetic prestack data in the t-x-offset domain
图3的地震波同相轴信息十分复杂,在构造拐点处有较强的散射波存在,并且复杂构造使得散射波与反射波同相轴有互相叠加的情况。对图3数据加上强能量的涌浪噪声,结果如图4所示。该噪声平均振幅值是有效信号的5倍,影响相邻连续几道,在地震记录上的形态呈条带状或一串斑点,对地震资料的中深层形成强烈的低频噪声背景。在此复杂波场条件下,很难用简单的去噪方法实现对该类型噪声的压制。
图5是对图4包含涌浪噪声的地震数据应用OC-Seislet正向变换后得到的变换域数据。即对图4数据进行速度分析后做NMO校正,然后对时间轴做拉伸变换,接下来对拉伸的时间轴和中心点坐标轴做二维傅里叶变换,最后在炮检距方向应用OC-Seislet变换,就得到了图5的频率(f)-波数(k)-级数域数据,级数坐标轴对应着图4中的炮检距轴。可以看到,反射波和散射波信息都被压缩在很小的动态级数范围内,而涌浪噪声由于不能被OC算子预测,所以在变换域中,涌浪噪声带来的假象依然遍布在整个变换域。

图4 包含涌浪噪声的叠前数据模型Fig.4 Synthetic prestack data with swell noise

图5 频率-波数-级数域内的OC-Seislet变换系数Fig.5 OC-Seislet coefficients in the f-k-scale domain

a. OC-Seislet变换;b.小波变换。图6 模型数据去除涌浪噪声结果Fig.6 Result after removing swell noise in the synthetic data

a. OC-Seislet变换;b.小波变换。图7 OC-Seislet变换和小波变换去除的噪声Fig.7 Noise removed by OC-Seislet transform and wavelet transform

图8 OC-Seislet变换及小波变换对海上实际数据的处理Fig. 8 Denoising field data by OC-Seislet transform and wavelet transform respectively
随后在变换域内选取适当的阈值参数进行软阈值处理,就能够分离信号和噪声。笔者选取百分位数软阈值方法进行处理,选取参数为1.3%。然后应用反向OC-Seislet变换,就能够重建波场信息,结果如图6a所示。可以观察到,涌浪噪声衰减明显、残留较少,并且在多条散射波同相轴叠加的位置,保幅去噪效果也很理想。为了验证复杂波场中OC-Seislet变换对涌浪噪声的衰减效果,选择小波变换与其进行对比。图6b是小波变换的去噪结果,可以看到,在涌浪噪声比较密集的位置,残留的噪声较严重,并且重建后的散射波同相轴也不清晰。
为了更直观地对比去噪效果,将OC-Seislet变换与小波变换的去噪结果分别与图4的含涌浪噪声数据做差,得到如图7a和图7b所示的差剖面。可以明显地观察到,应用OC-Seislet变换去噪(图7a)后的有效信号损失更小。

a.含涌浪噪声的数据;b OC-Seislet变换去除涌浪噪声结果后;c.小波变换去除涌浪噪声结果后。图9 叠加剖面图Fig. 9 Stacked Sections
3 实际数据测试
为了验证本方法的有效性,我们使用墨西哥湾某区域的海上实际数据进行测试。该数据具有非常复杂的构造,在数据中加入人工涌浪噪声,如图8a所示。针对涌浪噪声低频率、高振幅的特征,采用AB系数相似方法对数据做速度分析,得到的速度谱如图8b所示。
对数据做NMO处理后应用OC-Seislet正向变换,数据转变到图8c的频率-波数-级数域,OC算子将可预测的有效信号压缩到很小的范围内,不可预测的噪声则分散于整个变换域。
接下来,选取3.5%的阈值参数进行百分位数软阈值处理,在变换域将噪声引起的假象消除,再经由OC-Seislet反向变换,将数据转变回时间-共中心点-炮检距域,就得到了去除涌浪噪声后的数据(图8d)。反射波信息清晰,强能量的涌浪噪声得到了有效压制。
为验证OC-Seislet变换对含涌浪噪声的实际数据去噪效果,依旧选取小波变换与其进行对比(图8e)。可以观察到,小波变换对涌浪噪声密集区域的压制能力有限,并且去噪后有效信号能量较弱,构造信息不清晰。图8f和图8g分别为两种变换方法去噪结果的差剖面,明显可以观察到:小波变换去噪结果的差剖面(图8g)中,构造信息较为明显,说明小波变换在去除涌浪噪声的过程中,有效信号能量损失较为严重;而OC-Seislet变换去噪结果的差剖面(图8f)中,有效信号的损失很小,这说明应用OC-Seislet变换去除涌浪噪声,可以达到压制噪声的同时又保护有效信号的目的。
将含涌浪噪声的地震数据以及两种方法去噪后数据的叠加剖面图进行对比,如图9所示。通过对比结果可以看出,OC-Seislet变换对涌浪噪声压制效果明显,同时能够有效保护复杂构造下的有效信息。
4 结语
基于OC-Seislet变换的涌浪噪声阈值衰减方法以波动方程动力学关系为基础,能够准确地表征含涌浪噪声并且有着复杂同相轴关系的地震波场,有效地压缩复杂地震波同相轴,显著地改善地震资料的信噪比。模型试验中,通过对含有涌浪噪声并且存在散射波的复杂波场进行去噪处理,证明了该方法的有效性。将该方法用于实际地震资料中,也获得了理想的去噪效果。该方法的提出,为后续的处理工作提供了高品质的基础资料。
[1] Hassan H H, Peirce J W. Empirical Mode Decomposition (EMD) of Potential Field Data: Airborne Gravity Data as an Example[C]//SEG Technical Program Expanded Abstracts. [S.l.]:SEG, 2005: 704-706.
[2] 陈见伟. 深海地震资料叠前去噪方法研究[J]. 海洋石油, 2009, 28(2): 29-35. Cheng Jianwei. Study on Seismic Data Prestack Noise Attenuation Techniques in Deep Water[J]. Offshore Oil, 2009, 28(2): 29-35.
[3] 宋家文, 陈小宏, 刘国昌. 地震道随机重排联合EM算法衰减高振幅涌浪噪声[C]//中国地球物理学会第二十七届年会论文集. 北京:中国地球物理学会, 2011: 667. Song Jiawen, Chen Xiaohong, Liu Guochang. High-Amplitude Swell Noise Attenuation Using Seismic Trace Reordering and EM Algorithm[C]// 27th Annual Meeting Proceedings of Chinese Geophysical Society. Beijing: Chinese Geophysical Society, 2001: 667.
[4] 徐善辉. 基于Hilbert-Huang变换的地震噪声衰减与薄层预测技术研究[D]. 长春: 吉林大学, 2012. Xu Shanhui. The Study of Seismic Noise Attenuation and Thin-Layer Prediction Technique Based on Hilbert-Huang Transform[D]. Changchun: Jilin University, 2012.
[5] 周伟, 王瑞燕, 周卓月. 希尔伯特-黄变换在海浪资料分析中的应用[J]. 信息技术, 2014, 38(3): 43-46. Zhou Wei, Wang Ruiyan, Zhou Zhuoyue. Hilbert-Huang Transform Analysis of Wave Data[J]. Information Technology, 2014, 38(3): 43-46.
[6] 牛伟华, 吴春红. 海洋地震资料中强能量噪声压制的分频振幅衰减法应用研究[J]. 石油物探, 2013, 52(4): 394-401. Niu Weihua, Wu Chunhong. Application of Frequency-Dependent Amplitude Attenuation Method to Suppress Strong-Energy Noise in Offshore Seismic Data[J]. Geophysical Prospecting for Petroleum, 2013, 52(4): 394-401.
[7] Bekara M. Toward an Automatic Swell Noise Attenuation Process[C]// 76th EAGE Conference and Exhibition.[S.l.]:EAGE, 2014.
[8] Hu C, Lu W. A Hybrid Method for Strong Low-Frequency Noise Suppression in Prestack Seismic Data[J]. Journal of Applied Geophysics, 2014, 108: 78-89.
[9] 巩向博, 韩立国, 王恩利, 等. 压制噪声的高分辨率 Radon 变换法[J]. 吉林大学学报:地球科学版, 2009, 39(1): 152-157. Gong Xiangbo,Han Liguo,Wang Enli,et al.Denoising Via High Resolution Radon Transform[J]. Journal of Jilin University: Earth Science Edition, 2009, 39(1): 152-157.
[10] 王德利, 仝中飞, 唐晨, 等. Curvelet 阈值迭代法地震随机噪声压制[J]. 应用地球物理, 2010, 7(4): 315-324. Wang Deli,Tong Zhongfei,Tang Chen,et al.An Iterative Curvelet Thresholding Algorithm for Seismic Random Noise Attenuation[J]. Applied Geophysics, 2010, 7(4): 315-324.
[11] 李海山, 吴国忱, 印兴耀. 形态分量分析在去除地震资料随机噪声中的应用[J]. 吉林大学学报:地球科学版, 2012, 42(2): 554-561. Li Haishan, Wu Guochen, Yin Xingyao. Application of Morphological Component Analysis to Remove of Random Noise in Seismic Data[J]. Journal of Jilin University: Earth Science Edition, 2012,42(2): 554-561.
[12] 刘琼, 曹思远, 关守军. 基于小波域稀疏性的地震数据去噪[C]//中国地球物理第十九分会场论文集. 北京:中国地球物理学会, 2013: 610. Liu Qiong, Cao Siyuan, Guan Shoujun. Denoising of Seismic Data Based on Sparsity in Wavelet Domain[C]// 19th Session Proceedings of Chinese Geophysical. Beijing: Chinese Geophysical Society, 2013:610.
[13] 徐明华, 李瑞, 路交通, 等. 基于压缩感知理论的缺失地震数据重构方法[J]. 吉林大学学报:地球科学版, 2013,43(1):283-290. Xu Minghua, Li Rui, Lu Jiaotong, et al. Study on the Recovery of Aliasing Seismic Data Based on the Compressive Sensing Theory[J]. Journal of Jilin University: Earth Science Edition, 2013,43(1): 283-290.
[14] Fomel S. Towards the Seislet Transform[C]// SEG Expanded Abstracts of 76th Annual International Meeting. [S.l.]:SEG, 2006:2847-2851.
[15] Liu Y, Fomel S. OC-Seislet: Seislet Transform Construction with Differential Offset Continuation[J]. Geophysics, 2010, 75(6): 235-245.
[16] Fomel S. Theory of Differential Offset Continuation[J]. Geophysics, 2003, 68(2): 718-732.
[17] Sweldens W. Lifting Scheme: A New Philosophy in Biorthogonal Wavelet Constructions[C]// Wavelet Applications in Signal and Image Processing:III. [S.l.]:SPIE, 1995: 68-79.
[18] Sweldens W, Schröder P. Building Your Own Wavelets at Home[C]//Wavelets in Computer Graphics.New Orleans:SIGGRAPH, 1996:15-87.
[19] Fomel S. Applications of Plane-Wave Destruction Filters[J]. Geophysics, 2002, 67(6): 1946-1960.
[20] Fomel S, Liu Y. Seislet Transform and Seislet Frame[J]. Geophysics, 2010, 75(3): 25-38.
[21] Fomel S. Predictive Painting of 3D Seismic Volumes[J]. Geophysics, 2010, 75(4): 25-30.
[22] Fomel S. Velocity Analysis Using AB Semblance[J]. Geophysical Prospecting, 2009, 57(3): 311-321.
Swell Noise Attenuation Methods Based on OC-Seislet Transform
Gou Fuyan1, Liu Cai1, Liu Yang1, Wang Bo1,2, Feng Xuan1
1.CollegeofGeoExplorationScienceandTechnology,JilinUniversity,Changchun130026,China2.ExplorationTechnologyandEngineeringCollege,ShijiazhuangUniversityofEconomics,Shijiazhuang050031,China
In the process of the marine seismic acquisition, swell noise is a kind of common noise, which has low frequency, high energy, and long period. A general approach is difficult to achieve the balance between denoising and signal protection. According to the characteristics of the swell noise, we applied the OC-Seislet transform method based on wave-equation offset-continuation (OC) operator for denoising. The proposed method characterizes the complex seismic wavefield by OC operator, compresses the noise data by optimal transform-basis function, use soft threshold to separate the signals from noise in the transform domain, and then invert transform the interpolated result to the data domain so as to remove the swell noise. After applying the real data to the model, OC-Seislet transform method proves that it can remove the swell noise from the original data; meanwhile, it can protect seismic events even in a structural complex area.
offset continuation operator; OC-Seislet transform; swell noise; soft threshold
10.13278/j.cnki.jjuese.201503305.
2014-09-20
国家自然科学基金项目(41274119,41174080);国家“863”计划项目(2012AA09A20103)
勾福岩(1983--),男,博士研究生,主要从事地震数据处理等工作,E-mail:gouyuxin1010@sina.com
刘洋(1979--),男,教授,博士生导师,主要从事地震数据处理、海洋电磁数据处理和地质-地球物理综合研究等工作,E-mail:yangliu1979@jlu.edu.cn。
10.13278/j.cnki.jjuese.201503305
P631.4
A
勾福岩,刘财,刘洋,等. 基于OC-Seislet变换的海洋涌浪噪声衰减方法.吉林大学学报:地球科学版,2015,45(3):962-970.
Gou Fuyan, Liu Cai, Liu Yang, et al. Swell Noise Attenuation Methods Based on OC-Seislet Transform.Journal of Jilin University:Earth Science Edition,2015,45(3):962-970.doi:10.13278/j.cnki.jjuese.201503305.
