基于暂态电压扰动范围判别的自适应低压减载策略
2015-03-11刘巍李晔张保会雷俊哲
刘巍,李晔,张保会,雷俊哲
(1.国网河南省电力公司电力科学研究院,郑州市 450052;2.西安交通大学电气工程学院,西安市 710049)
基于暂态电压扰动范围判别的自适应低压减载策略
刘巍1,李晔2,张保会2,雷俊哲1
(1.国网河南省电力公司电力科学研究院,郑州市 450052;2.西安交通大学电气工程学院,西安市 710049)
传统低压减载方案仅根据本地电压信息动作,未考虑全网暂态电压响应特征。分析系统暂态电压跌落与扰动范围的关系,并基于负荷节点的电压偏移量提出暂态电压扰动范围判别指标,将电压扰动类型划分为全网暂态电压扰动和局部暂态电压扰动。以该指标的判别结果为基础,综合考虑扰动后系统电压与频率的动态过程,构建基于暂态电压扰动范围判别的自适应低压减载策略,该策略采用2套自适应减载方案分别应对全网暂态电压扰动和局部暂态电压扰动。对IEEE 39节点系统的仿真结果验证了该策略在应对不同失稳场景时的有效性和优越性。
电压稳定性;扰动范围;切负荷;频率动态;自适应控制
0 引 言
电压是电力系统电能质量的重要指标之一[1],电压稳定性、频率稳定性和功角稳定性被视为系统稳定性的三大方面[2-3]。目前,低压减载(undervoltage load shedding,UVLS)已被广泛用于防止电压崩溃事故的发生,但传统低压减载方案仅根据本地电压信息进行动作,一般设置有基本轮和特殊轮,当系统电压低于每轮门槛值后经过一定延时切除固定比例的负荷,由于各继电器间缺少信息交换,传统低压减载方案无法计及全网暂态电压响应情况及电压的时空分布特性,往往造成负荷的欠切或者过切,难以保障电力系统在发生严重故障时的暂态电压稳定性[4-5]。另外,传统低压减载未考虑系统频率响应,与低频减载(underfrequency load shedding,UFLS)相互独立,当电压失稳时,由于负荷有功的急剧下降,导致频率过高,造成发电机跳闸甚至引发大面积停电[6-8]。因此在考虑频率动态响应的基础上,设计一套能够有效应对系统严重扰动的自适应低压减载方案,具有重大的理论和实际意义。
目前,同步相量测量技术被认为是最先进且最精确的同步测量技术,它能够实时地追踪系统频率和电压等状态量的变化情况[9]。同步相量测量单元(phasor measurement unit,PMU)的不断发展,使得充分的信息交换成为可能,为自适应控制策略的实现提供了技术支撑[10-11]。文献[12]讨论了同步相量测量技术对于提高系统监测、保护和控制等方面的作用。文献[13]利用同步相量测量装置实现对电压失稳问题的预测。文献[14]分析了同步相量测量装置在广域测量系统(wide-area measurement system,WAMS)中的作用,提出了利用电压跌落值ΔU和电压稳定判别指标VQS分配切负荷量。文献[15]提出了衡量电压暂态失稳程度的L指标,并基于WAMS构建了自适应切负荷方案。文献[16]综合考虑了系统的频率和电压响应,并且提出利用频率跌落值Δf和电压稳定性判别指标VQS,根据潮流追踪法分别计算负荷的有功切除量和无功切除量。
可以看出,学者们已经对自适应低压减载进行了有益的探索,但是上述方案都需要获得较多的系统响应信息以及网络结构信息,并且往往是在全网进行切负荷操作,缺少对电压时空分布特性和暂态电压扰动范围的考虑。
本文仿真分析了系统暂态电压跌落与扰动范围的关系,并基于负荷节点的电压偏移量提出了暂态电压扰动范围判别指标,通过该指标将电压扰动类型划分为全网暂态电压扰动和局部暂态电压扰动。以该指标的判别结果为基础,本文综合考虑了扰动后系统电压与频率的动态过程,构建了基于暂态电压扰动范围判别的自适应低压减载策略,该策略采用2套自适应减载方案来分别应对全网暂态电压扰动问题和局部暂态电压扰动问题。对IEEE 39 节点系统的仿真结果验证了该策略在应对不同失稳场景时的有效性和优越性。
1 暂态电压扰动范围判别指标
当系统出现扰动时,负荷节点电压下降。负荷节点电压的跌落程度不仅受发电机励磁调节器、系统无功充裕程度、网络的拓扑结构以及负荷的电压特性等因素的影响,还受到故障扰动地点的影响。相同的扰动量出现在系统的不同地点,造成的暂态电压扰动范围及电压跌落程度也有所不同。
图1为IEEE 39节点系统,考虑发电机调压器和调速器,负荷采用70%电动机和30%恒阻抗并联模型[17],电动机考虑转子电磁暂态,在PSASP上进行仿真。图2和图3为相同大小有功缺额分布在不同地点的暂态电压偏移对比图。

图1 IEEE 39节点系统Fig.1 IEEE 39-bus system
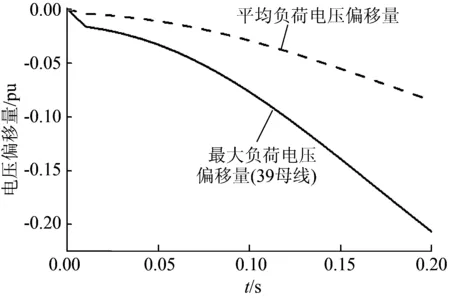
图2 负荷电压偏移量(39母线)Fig.2 Voltage offset of load(39 bus)
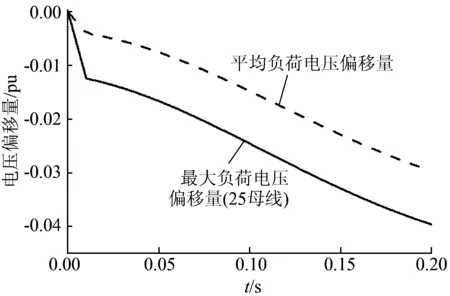
图3 负荷电压偏移量(25母线)Fig.3 Voltage offset of load(25 bus)
图2所设故障为39机脱落有功1 000 MW。系统的最大负荷电压偏移量出现在39负荷母线,其暂态电压在故障后0.2 s已跌落超过-0.2 pu,而此时的系统平均负荷电压偏移量仅为-0.085 pu,最大负荷电压偏移量超过平均负荷电压偏移量的2倍。
图3所设故障为30,32,33和38机分别脱落有功250 MW,总有功缺额也为1 000 MW。系统的最大负荷电压偏移量出现在25负荷母线,其暂态电压在故障后0.2 s内的跌落值为-0.039 pu,此时的系统平均负荷电压偏移量为-0.030 pu,与最大负荷电压偏移量相差不大。
对比图2和3可知,相同有功缺额在系统的分布不同,暂态电压扰动范围也有所不同。有功缺额分布越集中,最大负荷电压偏移量与平均负荷电压量相差倍数越大,暂态电压的扰动范围越集中。
因此,本文通过比较最大负荷电压偏移量与平均负荷电压偏移量,将暂态电压扰动划分为局部暂态电压扰动和全网暂态电压扰动,并采用电压跌落幅值按如下步骤判别暂态电压扰动范围。
(1)计算全网各负荷节点的电压跌落幅值。
通过广域测量系统计算电力系统在故障发生后0.2 s内各负荷节点的电压跌落值:
ΔUj=Uj-Uj0,j=1,2,…,N
(1)
式中:j为负荷节点号;ΔUj为第j个负荷节点的电压跌落值;Uj为故障后0.2 s时第j个负荷节点的电压;Uj0为故障前第j个负荷节点的电压;N为负荷节点总数。
(2)按照电压跌落幅值大小对各负荷节点进行排序,使得:
(2)
注意:对负荷节点排序时,不考虑负荷电压升高即ΔUj为正数的节点。
(3)计算负荷节点的平均电压偏移量ΔUav:
(3)
(4)判别暂态电压扰动范围。
若最大负荷电压偏移量小于平均负荷电压偏移量的2倍即满足式(4),则判断该扰动为全网暂态电压扰动,即
ΔUmax<2ΔUav
(4)
若最大负荷电压偏移量大于或等于平均负荷电压偏移量的2倍即满足式(5),则判断该扰动为局部暂态电压扰动,即
ΔUmax≥2ΔUav
(5)
2 基于暂态电压扰动范围判别的自适应低压减载新策略
2.1 有功缺额获取
系统发生严重扰动出现有功不平衡量时,可通过广域测量系统追踪全网各机组的频率动态变化过程,从而按式(6)根据各机组的频率变化率计算系统的有功缺额大小,即
(6)
式中:i为发电机组号;N0为发电机总数;ΔPi为第i台发电机有功缺额;Ti为第i台发电机的惯性时间常数;Si为第i台发电机额定容量;fn为额定频率50 Hz;dfi/dt为通过广域测量系统获得的第i台发电机在故障后0.2 s时的频率变化率;fc为系统等效惯性中心频率。
2.2 切负荷量分配
当系统发生负荷电压跌落时,先按照暂态电压扰动范围判别指标确定暂态电压扰动的范围,若扰动类型为全网暂态电压扰动,则采用全网切负荷控制方案,若扰动类型为局部暂态电压扰动,则采用局部切负荷控制方案。
(1)全网切负荷方案:在所有负荷节点进行切负荷操作,各负荷节点的切负荷量按照其电压跌落幅值大小根据式(7)和(8)进行分配,即:
(7)
ΔPj=wjΔP,j=1,2,…,N
(8)
式中:wj为第j个切负荷节点的电压偏移量占所有负荷节点电压偏移量总和的比例即切负荷分配比例;ΔPj为第j个切负荷节点的切负荷量;ΔP为由式(6)求得的全网有功缺额。
(2)局部切负荷方案:从电压跌落最严重的负荷节点即|ΔUj|最大的节点开始进行切负荷操作,直到所切除负荷量与有功缺额总量相等,即
(9)
式中M为进行切负荷节点的个数。
具体的方案流程图如图4所示。
3 仿真结果分析
本文仿真分析了在全网电压扰动和局部电压扰动下新策略的低压减载效果,仿真结果验证了新方案相较于传统低压减载方案在应对不同失稳场景时的有效性和优越性。
3.1 失稳场景一:局部电压失稳
0.5 s时IEEE 39节点系统31号机跳闸,同时14-4与11-6这2条线路跳开,通过各机组频率响应可测得系统故障后0.2 s时的有功缺额为520.22 MW。

图4 自适应低压减载方案流程图Fig.4 Adaptive scheme of UVLS
如图5所示,该故障将造成负荷节点电压失稳,并且不同母线的电压跌落速度、电压偏移幅度相差较大。图6为各机组频率响应曲线,由于感应电动机堵转,使得负荷的有功功率急剧下降,导致除39机外的机组频率在跌落约0.1 Hz后又迅速上升至51 Hz。另外,由于出现了功角失稳(39号机组失步),使得频率和电压在失稳过程中发生振荡。
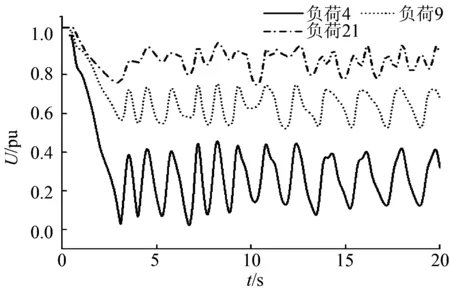
图5 负荷电压响应Fig.5 Voltage responses of loads
图7~9为本文的自适应低压减载方案与传统低压减载方案的效果对比图。传统低压减载方案定义如表1所示,共设5个基本轮和1个特殊轮,总切负荷率可达45%。在此故障扰动下,传统方案将切除1 215.90 MW。而对于本文的自适应低压减载方案,由于故障后0.2 s系统最大负荷电压偏移量为-0.17 pu(31母线),而系统平均负荷电压偏移量为-0.05 pu,满足式(5),因此采用局部切负荷方案:依次切除31母线负荷、7母线负荷以及55.45%的4母线负荷,共520.22 MW。此方案比传统方案少切除695.68 MW。

图6 机组频率响应Fig.6 Frequency responses of generators
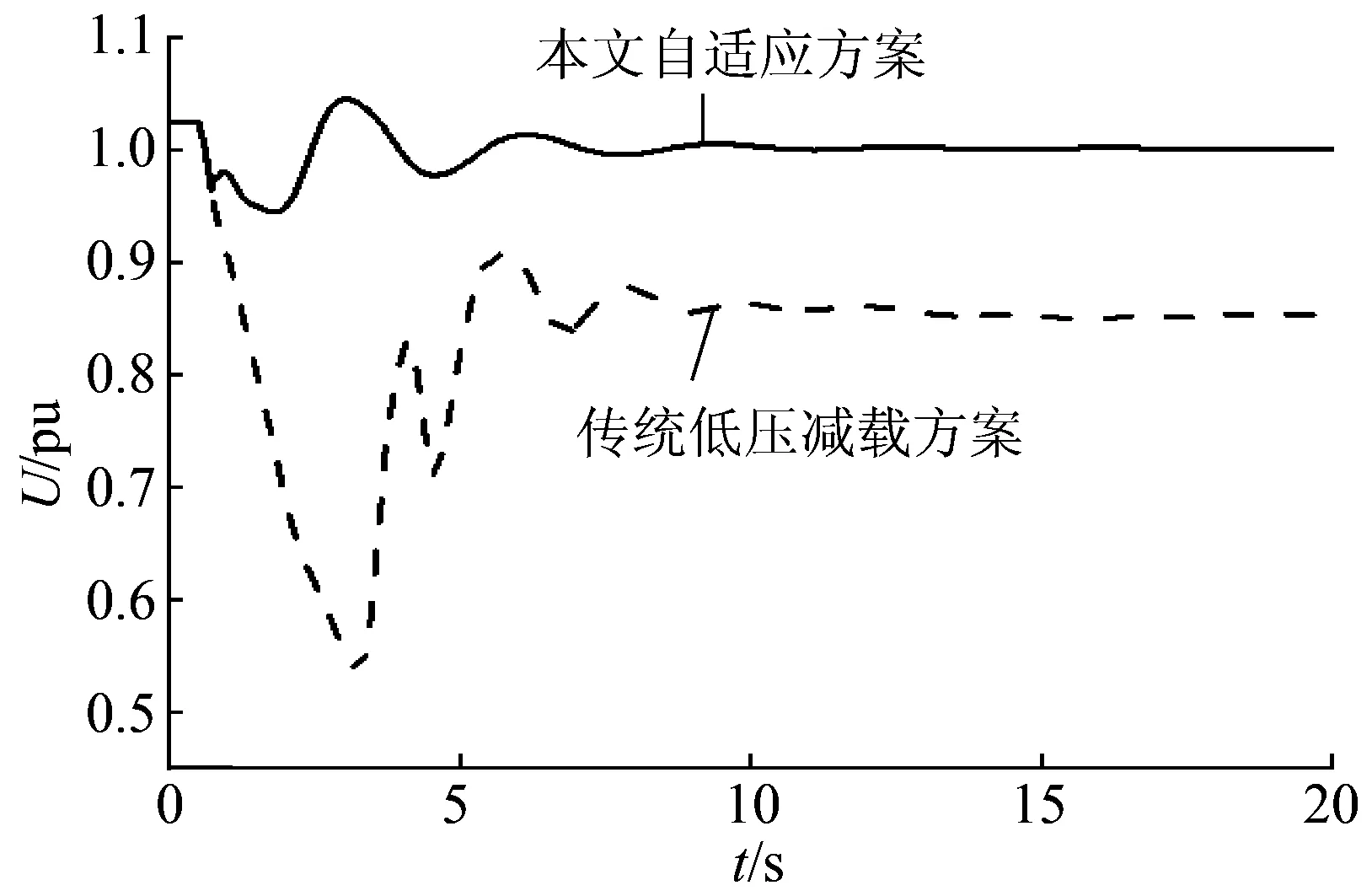
图7 减载后负荷平均电压Fig.7 Average voltage of load after UVLS
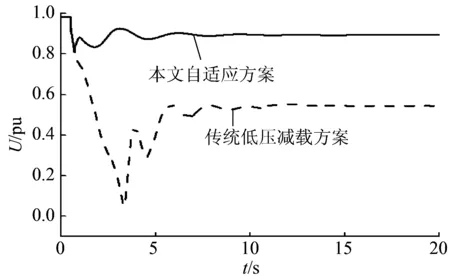
图8 减载后31母线电压Fig.8 Bus-31 voltage after UVLS
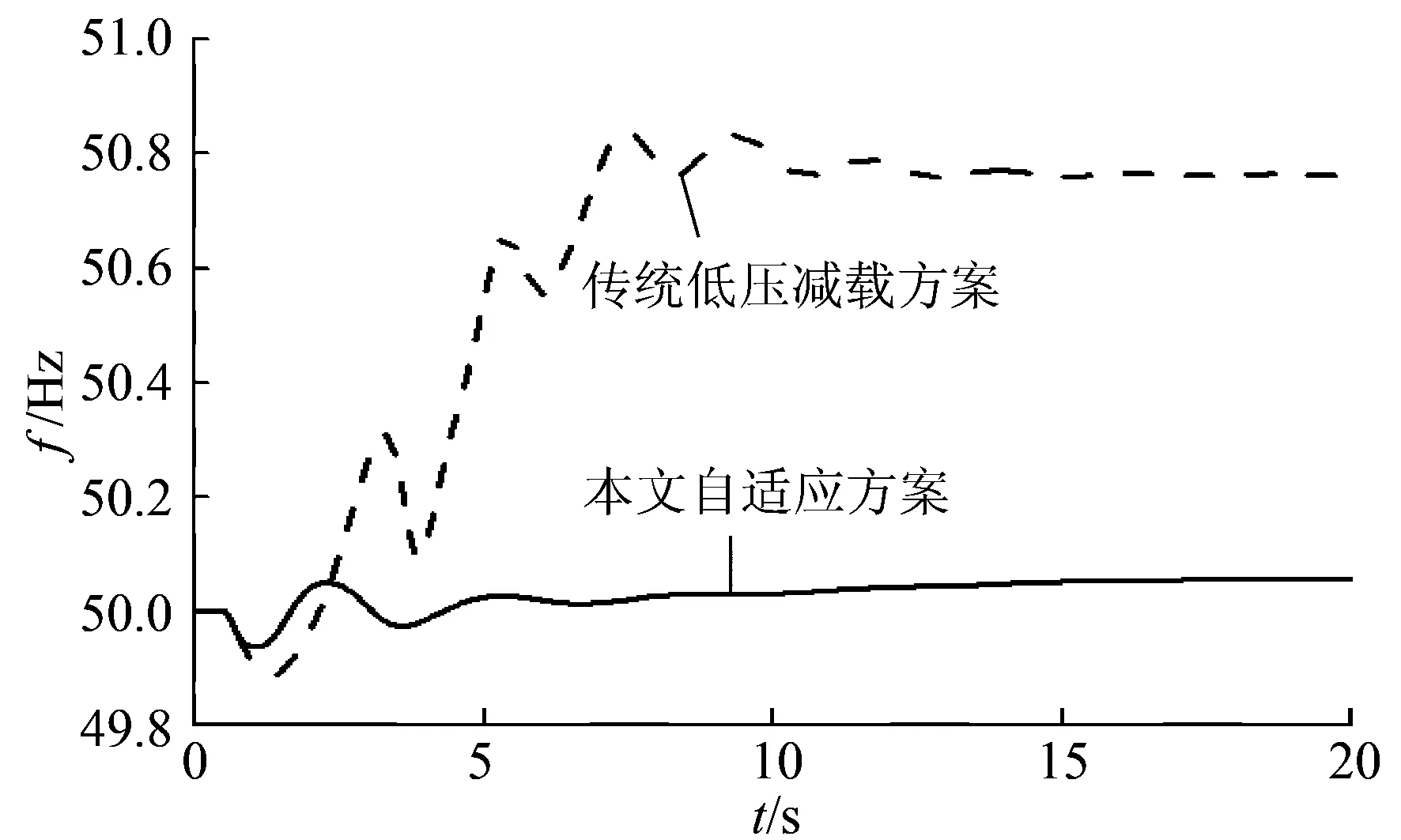
图9 减载后机组惯性中心频率Fig.9 Frequency of inertia center after UVLS
表1 传统低压减载方案
Table 1 Conventional UVLS schemes

从图7可以看出,虽然传统方案切除负荷更多,但是由于各处低压减载装置需要逐轮动作,负荷的切除时间晚,使得负荷电压恢复较慢,恢复后的稳态值过低。由图8可以看出,利用传统方案系统依然发生局部电压失稳,其中31母线电压将低于0.6 pu,且由于电压失稳使得负荷有功功率降低,最终导致频率升至50.8 Hz(如图9所示)。利用本文的自适应低压减载方案,在局部减载后使得系统平均电压迅速恢复至额定值,最低电压(31母线电压)也恢复至接近0.9 pu,并且频率偏差不超过±0.1 Hz,减载效果明显优于传统低压减载方案。
3.2 失稳场景二:全网电压失稳
0.5 s时IEEE 39节点系统30,32和38机组相继跳闸,根据其余机组的频率响应可测得系统故障后0.2 s时的有功缺额为1 730 MW。如图10所示,系统将发生大面积电压失稳,振荡剧烈,并且不同负荷母线的电压跌落速度、电压偏移幅度相差很小。图11为各机组频率响应曲线,39机组与其他机组失步,并且除39机外的其余机组在故障后约0.4 s频率均跌至49.7 Hz以下,而后由于感应电动机堵转,使得机组频率超出51 Hz。
图12为本文的自适应低压减载方案与传统低压减载方案的效果对比图。传统低压减载方案定义如表1所示,在此故障扰动下,传统方案将切除1 978.92 MW。对于本文的自适应减载方案,由于故障后0.2 s系统最大负荷电压偏移量为-0.13 pu(28母线),而系统平均负荷电压偏移量为-0.10 pu,满足式(4),因此采用全网切负荷方案,在所有负荷节点按照电压跌落幅度进行切负荷量的分配,共切除负荷1 730 MW,比传统方案少切除248.92 MW。
从图12可以看出,传统低压减载方案在减载后仍发生大面积电压崩溃,并由于机组的失步出现严重振荡;利用本文的自适应方案进行减载后,负荷平均电压可以在故障后1 s内迅速恢复至额定值以上,且电压在恢复过程中振荡幅度小,在故障后5 s时负荷电压基本达到新的稳定状态。

图10 负荷电压响应Fig.10 Voltage response of loads

图11 机组频率响应Fig.11 Frequency responses of generators

图12 减载后负荷平均电压Fig.12 Average voltage of load after UVLS
4 结 论
相同扰动量出现在系统的不同地点,造成的暂态电压扰动范围有所不同。扰动越集中,系统中不同负荷母线的暂态电压跌落程度相差越大;扰动越分散,不同负荷母线的暂态电压跌落程度相差越小。基于此,本文通过比较最大负荷电压偏移量与系统平均负荷电压偏移量,提出了暂态电压扰动范围判别指标,将暂态电压扰动类型划分为全网暂态电压扰动和局部暂态电压扰动。
以暂态电压扰动范围判别指标的判别结果为基础,本文综合考虑了扰动后系统电压与频率的动态过程,构建了基于暂态电压扰动范围判别的自适应低压减载策略,该策略采用2套自适应减载方案来分别应对全网暂态电压扰动问题和局部暂态电压扰动问题。相较于传统的逐轮次低压减载方案,本方案具有动作迅速、切负荷量小等优点,并且能使系统具有更优的动态恢复过程和稳态恢复指标,能有效地保障电力系统在大扰动后的暂态电压的稳定性,同时也有利于减小扰动过程中系统频率的偏移量。
[1]孙华东,汤涌,马世英.电力系统稳定的定义与分类评述[J].电网技术,2006,30(17):31-35.Sun Huadong,Tang Yong,Ma Shiying.A commentary on definition and classification of power system stability[J].Power System Technology,2006,30(17):31-35.
[2]薛禹胜.时空协调的大停电防御框架:(三)各道防线内部的优化和不同防线之间的协调[J].电力系统自动化,2006,30(3):1-10,106.Xue Yusheng.Space-time cooperative framework for defending blackouts: Part Ⅲ optimization and coordination of defense-lines[J].Automation of Electric Power Systems, 2006, 30(3): 1-10,106.
[3]Sigrist L,Egido I,Rouco L.Frequency stability boundary of small isolated power systems[J].Electric and Electronics Engineers,2010:229-233.
[4]马世英,易俊,孙华东,等.电力系统低压减载配置原则及方案[J].电力系统自动化,2009,33(5):45-49.Ma Shiying,Yi Jun,Sun Huadong, et al.Study on configuration of under-voltage load shedding in power systems[J].Automation of Electric Power Systems,2009,33(5):45-49.
[5]邢国华,乔卫东.低压减载方案研究综述[J].华东电力,2005,33(12):23-26.Xing Guohua, Qiao Weidong.Study of undervoltage load shedding schemes[J].East China Electric Power,2005,33(12):23-26.
[6]薛禹胜,任先成,WU Q H,等.关于低频低压切负荷决策优化协调的的评述[J].电力系统自动化,2009,33(9):100-107.Xue Yusheng,Ren Xiancheng,WU Q H,et al.A review on optimization and coordination of under frequency/voltage load shedding[J].Automation of Electric Power Systems, 2009,33(9):100-107.
[7]陈树勇,朱琳,丁剑,等.风电场并网对孤网高频切机的影响研究[J].电网技术,2012,36(1):58-64.Chen Shuyong, Zhu Lin, Ding Jian, et al.Impact of grid-connected wind farms on high frequency generator tripping in isolated power grid[J].Power System Technology,2012,36(1):58-64.
[8]王一振,马世英,王青,等.电力系统孤网高频问题研究现状和发展趋势[J].电网技术,2012,36(12):165-169.Wang Yizhen, Ma Shiying, Wang Qing, et al.Present status and developing trend of research on over frequency in isolated power grid[J].Power System Technology,2012,36(12):165-169.
[9]Novosel D,Madani V,Bhargava B,et al.Dawn of the grid synchronization:Benefits,practical applications,and deployment strategies for wide area monitoring,protection,and control[J].IEEE Power Energy Magazine,2008,6(1):49-60.
[10]Cai J Y,Huang Zhenyu,Hauer J,et al.Current status and experience of WAMS implementation in North America [C]//Transmission and Distribution Conference and Exhibition,2005:1-7.
[11]Xie Xiaorong,Xin Yaozhong,Xiao Jinyu,et al.WAMS applications in Chinese power systems[J].IEEE Power Energy Magazine,2006,6(1):54-63.
[12]De La Ree Jaime,Centeno V,Thorp J S,et al.Synchronized.Phasor measurement applications in power systems[J].IEEE Transactions on Smart Grid,2010,1(1):20-27.
[13]Glavic M,Van Cutsem T.Wide-area detection of voltage instability from synchronized phasor measurements[J].IEEE Transactions on Power Systems,2009,24(3):1408-1416.
[14]Prasetijo D,Lachs W R,Sutanto D.A new load shedding scheme for limiting underfrequency[J].IEEE Transactions on Power Systems,1994,9(3):1371-1378.
[15]Seethalekshmi K,Singh S N,Srivastava S C.WAMS assisted frequency and voltage stability based adaptive load shedding[J].IEEE Power and Energy Society General Meeting.IEEE,2009:1-8.
[16]Tang Junjie,Liu Junqi,Ferdinanda Ponci,et al.Adaptive load shedding based on combined frequency and voltage stability assessment using synchrophasor measurements[J].IEEE Transactions on Power Systems,2013,28(2):2035-2047.
[17]Aboul-Seoud T,Jatskevich J.Dynamic modeling of induction motor loads for transient voltage stability studies[C]//Electric Power Conference.Canada:IEEE,2008:1-5.
(编辑:张媛媛)
Adaptive Undervoltage Load Shedding Strategy Based on Disturbance Scale Discrimination of Transient Voltage
LIU Wei1, LI Ye2, ZHANG Baohui2, LEI Junzhe1
(1.State Grid Henan Electric Power Research, Zhengzhou 450052, China;2.School of Electrical Engineering, Xi’an Jiaotong University, Xi’an 710049, China)
Conventional undervoltage load shedding(UVLS) scheme only focuses on local voltages without considering the response characteristics of transient voltage in whole gird.This paper analyzed the relationship between transient voltage drops and disturbance scale, proposed discriminant index for the disturbance scale of transient voltages based on the offset of voltage drops, and divided the transient voltage disturbance into two categories: the whole-grid transient voltage disturbance and the partial-region transient voltage disturbance.On the basis of the discriminant index results, an adaptive UVLS strategy based on the disturbance scale discrimination of transient voltages was constructed, with consideration on the dynamic process of voltage and frequency after the disturbance, which could solve the whole-grid transient voltage disturbance and the partial-grid transient voltage disturbance respectively with two adaptive load shedding schemes.Finally, the effectiveness and superiority of this strategy in different instability scenarios were verified by the simulation on the IEEE 39-bus system.
voltage stability; disturbance scale; load shedding; dynamic frequency; adaptive control
TM 712
A
1000-7229(2015)03-0065-06
10.3969/j.issn.1000-7229.2015.03.011
2014-10-14
2014-11-06
刘巍(1977),女,高级工程师,硕士,主要从事电力系统安全稳定控制和电力系统风险管理等方面研究工作;
李晔(1990),男,硕士研究生,本文通讯作者,主要研究方向为电力系统电压稳定性控制;
张保会(1953),男,教授,博士生导师,主要研究方向为电力系统继电保护,安全稳定控制和电力系统通信等;
雷俊哲(1984),男,工程师,硕士,主要从事电力系统安全稳定控制和电力系统风险管理等方面的研究工作。
