基于云模型的输电网规划方案综合决策方法

董美玲，游大海，王刚，陈伟华

(强电磁工程与新技术国家重点实验室(华中科技大学),武汉市430074)



基于云模型的输电网规划方案综合决策方法

董美玲，游大海，王刚，陈伟华

(强电磁工程与新技术国家重点实验室(华中科技大学),武汉市430074)

针对目前输电网规划方案综合决策中存在不确定因素以及确定指标权重方法主观性强的问题，提出了基于组合权重和云模型的输电网规划方案综合决策方法。该方法首先基于层次分析法、序关系法计算的主观权重和熵权法、变异系数法计算的客观权重，利用粒子群优化算法求取各评价指标的组合权重，克服了单一专家赋权或客观赋权的不足。然后采用云模型对各方案进行优劣排序，充分发挥了云模型能反映评价信息的模糊性和随机性的优势。最后结合IEEE Garver-6算例验证了该决策方法的有效性。

输电网规划方案；综合决策；组合权重；云模型；粒子群优化算法

0 引 言

输电网规划是根据电力系统的负荷预测及电源规划对输电系统的主要网架做出发展规划[1]。输电网规划的基本要求是确保输送容量、供电可靠性等，组合电力系统各部分使其整体结构运行效率最高，经济上最合理，并能充分适应系统日后发展的需要。一般将输电网规划问题分为2个阶段：建立优化模型产生待选方案和方案比选综合决策。输电网规划方案综合决策是对待选方案就其安全性、可靠性、经济性、适应性等各项指标进行综合评价，最终决策出综合最优的规划方案。

目前，输电网规划方案的综合决策方法主要是基于专家评判的模糊评价法和层次分析法，这2种方法均受专家知识、经验、偏好的制约，没有充分利用客观数据所提供的信息，主观性和偶然性较强。为解决模糊综合评价中确定指标权重主观性强的问题，文献[2]将熵权法引入模糊综合评价。文献[3]将数据包络法应用于配电网规划方案综合决策，具有一定的应用价值，但不适用于评价指标过多、过于复杂的情况。文献[4]将主成分分析法应用于解决输电网规划方案的综合决策问题，权重的确定完全依赖客观数据特征，减少了评价过程中的主观因素的影响，但是主成分分析法要求有大量样本数据，给实际操作带来困难。文献[5]在输电网规划综合决策中应用了灰色关联分析法，充分利用了客观数据信息。灰色关联分析法能够处理信息不完全明确的灰色系统，对于小样本无规律指标的评价问题准确性较高，但较难处理信息量庞大的评价对象。

本文将组合权重和云模型结合应用于输电网规划方案的综合决策。鉴于主、客观赋权法各自的特点和缺陷，基于熵值法和变异系数法确定的客观权重和层次分析法、序关系法确定的主观权重，利用粒子群优化算法确定各指标的权重系数[6]。而云模型能充分反映评价信息的模糊性和随机性，实现定量和定性之间的相互转换，更客观全面地评价各输电网规划方案，提高综合评价决策结果的可信度。

1 云模型相关概念

基于概率论和模糊数学，我国工程院院士李毅德教授于1995年提出了云的概念[7]，是将某个自然语言值表示的定性概念转化成定量表示的不确定性转换模型。设U是一个用精确数值表示的定量论域，C是U上的定性概念，若给定参数x∈U是定性概念C的一次随机出现，x对C的确定度u(x)∈[0,1]是有稳定倾向的随机数：u:U→[0,1], ∀x∈U,x→u(x)。则x在论域U上的分布称为云，即为云C(x)。每1个[x,u(x)]称为1个云滴。

研究表明，具有普遍适用性的是正态隶属云[8]，正态隶属云可由3个数字特征来刻画：期望值Ex、熵En和超熵He。Ex反映了定性概念的云滴群的重心位置。En体现了定性概念的随机性和模糊性：一方面En是定性概念随机性的度量，反映隶属于这个定性概念的云滴的离散程度；另一方面又体现了模糊概念的亦此亦彼性的裕度，反映了论域空间中可被该概念接受的云滴的取值范围。He是熵的不确定性的度量，即熵的熵，反映了云滴的凝聚度。

利用云的3个数字特征可以构造正态云模型发生器，生成云滴，生成算法如下：

(4)重复步骤(1)～(3)，直至产生足够数量的云滴。

2 基于组合权重和云模型的输电网规划综合决策过程

基于组合权重和云模型的输电网规划综合决策过程具体步骤如下。

(1)建立指标集。根据评价对象建立指标集：U={U1,U2,…,Um}，m为评价指标的个数。

(2)建立描述评价集云模型。根据构建的指标集，建立评价集V={V1,V2,…,Vn}，Vi(i=1,2，…，n)是对指标评语等级的模糊描述。本文采用基于黄金分割率的模型驱动法对云模型评价集进行划分。即在[0,1]之间，划分5个评价等级，各等级的云模型数字特征如表1所示。

表1 评价集云模型数字特征

Table 1 Numerical characteristics of evaluation sets’ cloud model

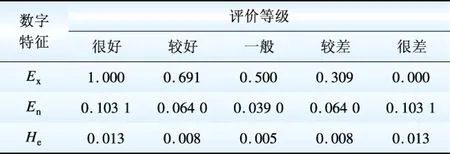
利用上节所述的正态云模型发生器算法，各等级均生成1 000个云滴，最终构成的评价集云模型如图1所示。

图1 评价集云模型Fig.1 Cloud model of evaluation sets

该图显示了各评语等级对应的隶属云，云的几何形状较好地反映了定性概念与其定量转换的不确定性。

(3)指标的无量纲化处理。根据评价指标集采集各待选方案数据，并对其进行无量纲化处理，使得指标数据更加客观有效。评价指标可分为定量指标和定性指标。对于定量指标可分为效益型(越大越好)、成本型(越小越好)和固定型(在某一固定点值附近最好)，分别进行归一化处理，使之成为[0,1]的某个值，且数值越大越好。

效益型指标无量纲化公式：

(1)

成本型指标无量纲化公式：

(2)

固定型指标无量纲化公式：

(3)

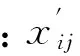
对于定性指标，需要将其自然语言描述转换成数值表示，而云模型可以综合定性概念的随机性和模糊性，用3个数字特征来描述整个云团，实现定性和定量之间的转换。因此可根据多位专家意见，将定性指标转化成云模型表示[9]。具体而言，通过h位专家对定性指标进行语言型评判，在本文中评语等级分为“很好”、“较好”、“一般”、“较差”、“很差”5种。每个评语等级均有1个云模型与之对应，如表1所示。则h个语言型评价值可表示为一个综合云模型：

(4)

En=En1+En2+…+Enh

(5)

式中：Exi(i=1,2,…,h)表示第i个专家认为该指标所属评语等级的云模型期望值；Eni(i=1,2,…,h)表示第i个专家认为该指标所属评语等级的云模型的熵。

由此得到每个定性指标的期望值Ex即可作为该指标的量化值，然后再根据定量指标的无量纲公式对其进行归一化处理。

(4)计算指标的组合权重。层次分析法能够解决多层相关因素构成的复杂系统的决策问题，是一种实用的多目标决策方法[10]。层次分析法根据专家意见，采用1～9标度法比较各元素间的相对重要性，构造相对于上一层元素重要性的判断矩阵，再根据最大特征根法求取各元素的局部权重。层次分析法充分尊重专家经验，所计算出的指标权重具有一定实用价值。

针对层次分析法存在的一致性问题，1992年中国学者郭亚军提出了序关系法[11]。序关系法无需构造判断矩阵，只要对各指标重要性进行排序，并依次比较前后相邻指标的重要度，最终计算得到各指标的权重，并且无需进行一致性校验。

熵权法是一种依据各指标的变异程度大小来确定指标权重的客观赋权法[2,5]。某个指标值变异程度越大，信息熵越小，提供的信息量越多，在综合评价中起的作用也就越大，则该指标的权重也应越大。熵权法数学原理清晰，有效利用了指标数据的客观信息，避免了指标赋权的主观随意性。

变异系数法原理类似于熵权法，其基本理念为某指标的变异系数(标准差)越大，则在综合评价中该指标提供的信息量越大，在综合评价中所起的作用越大，其权重越大[12]。

为了充分利用各种权重求取方法得出的权重信息，本文构建求取组合权重的优化模型，并应用粒子群优化算法进行求解。具体而言，通过引入权重求取方法加权系数θ的概念，将每个指标的组合权重表示成各种权重求取方法求得的结果的加权之和，基于组合权重向量与原有主、客观权重偏差尽量小的思想，建立如下模型：

(6)

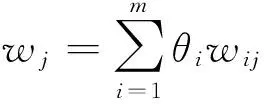
(7)

0≤θi≤1

(8)

(9)

式中：W=(w1,w2,…,wj,…,wn)为组合权重向量；wij为第i种权重求取方法求得的第j个指标的权重；m为权重求取方法数量；n为指标数量；θi为第i种权重求取方法的加权系数。

利用粒子群算法求解时，基于组合权重向量与各种权重求取方法的求取结果偏差之和最小目标，首先求出各种权重求取方法的加权系数θ，进而得到组合权重向量。该方法既充分利用了各种权重求取方法的优点，又避免了人为选择权重求取方法的主观随意性，因此求取的组合权重结果较为客观全面。

(10)

计算出的关联度k是个有稳定倾向的随机数，由此体现了云模型能反映评价信息的模糊性，而不是简单地将指标归属于某一个评语等级，使得评价结果更为科学客观。通过各指标与各评语等级云模型的关联度的计算，可以得到综合评判矩阵Dm×n，其中Dij表示第i个指标属于第j个评语等级云的关联度。

将综合评判矩阵D与综合权重向量W相乘，并归一化后可得到综合评判结果向量B：

B=W×D=[b1,b2,…bn]

(11)

式中bi(i=1,2,…n)表示被评价的规划方案整体属于第i个评语等级的隶属度。

进一步利用加权求和法得出评判结果得分r为

(12)

式中fi表示等级i的得分值，得分值越高表明该规划方案的评价结果越好。本文评判等级1～5对应的分数依次取值为5、4、3、2、1。

通过比较各方案的评判结果得分，可对各方案进行优劣排序，挑选出最优方案。

3 案例分析

选取输电网规划经典算例 IEEE Garver-6 系统[13]中3个备选方案进行算例分析。备选方案依次为“N”安全准则下的最小费用方案(方案1)，“N1”准则下的最小费用方案(方案2)及其次优方案(方案3)，如图2所示，图中实线、虚线分别代表已建线路、新建线路。

基于输电网规划的本质要求，本文建立了包含经济性、可靠性、社会影响性、适应性等方面的综合评价指标体系[14]，如表2所示。表3给出了各定量指标的类型以及相应的无量纲化参数，以及3个方案的定量指标数据。其中，本文认为重载线路为负载率在0.9以上的线路，电量不足期望值只考虑1条线路故障的情况。

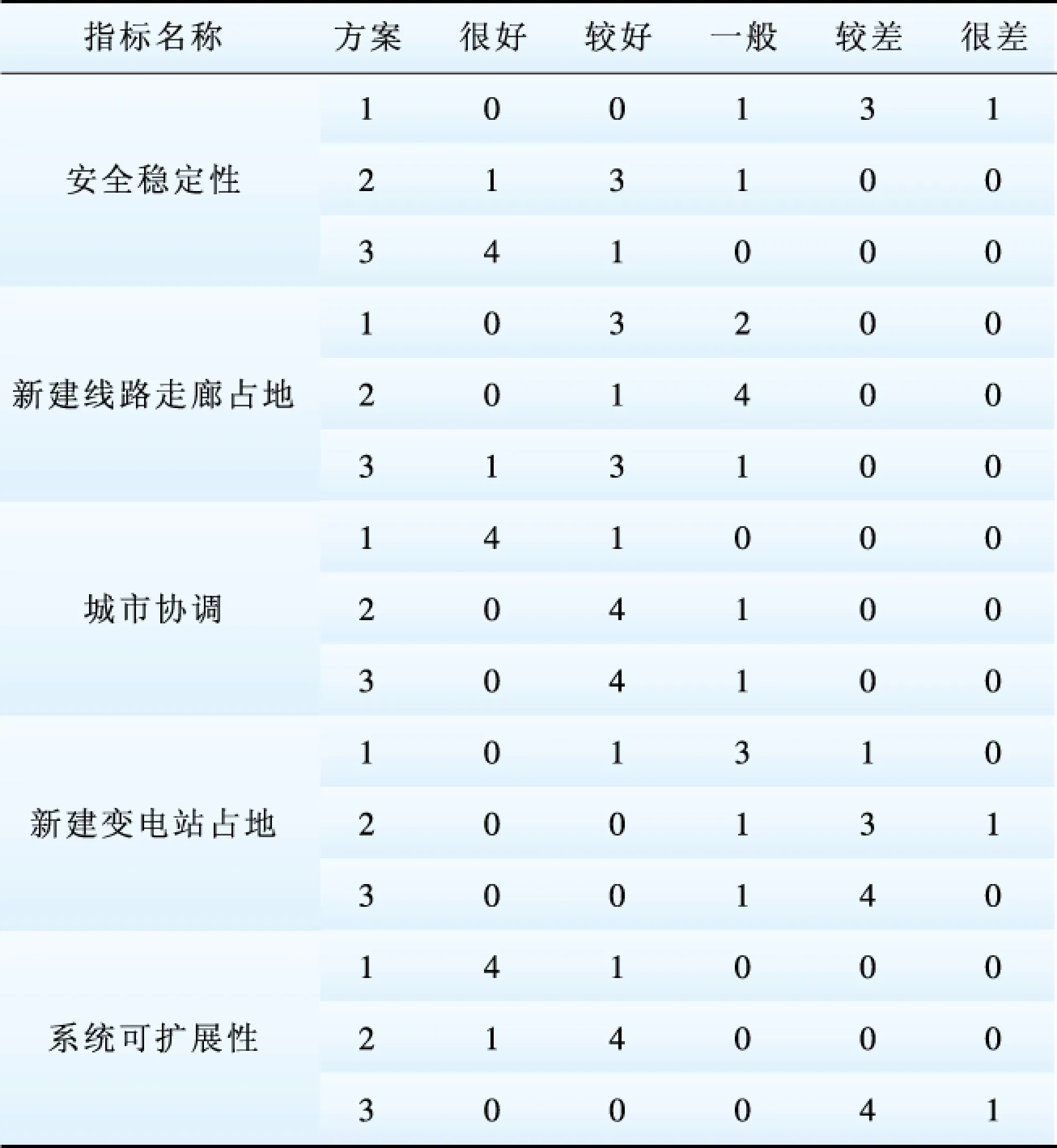
根据上一节给出的各种类型指标的无量纲化公式(1)～(3)对定量指标进行无量纲化处理，得到各定量指标归一化结果，如表4所示。对于定性指标，可根据几位专家意见，归为很好、较好、一般、较差、很差5个等级，再由云模型将定性指标定量化。本文通过5位专家对各方案的定性指标进行评判，统计将各方案的各个指标归为各档的专家人数，如表5所示。

根据式(4)求得3个方案定性指标的量化结果如表6所示。

根据文献[14]构造各评价指标的专家判断矩阵，利用层次分析法计算得到各指标的权重向量：

图2 待选方案结构Fig.2 Alternative scheme structure表2 评价指标集Table 2 Evaluation index set

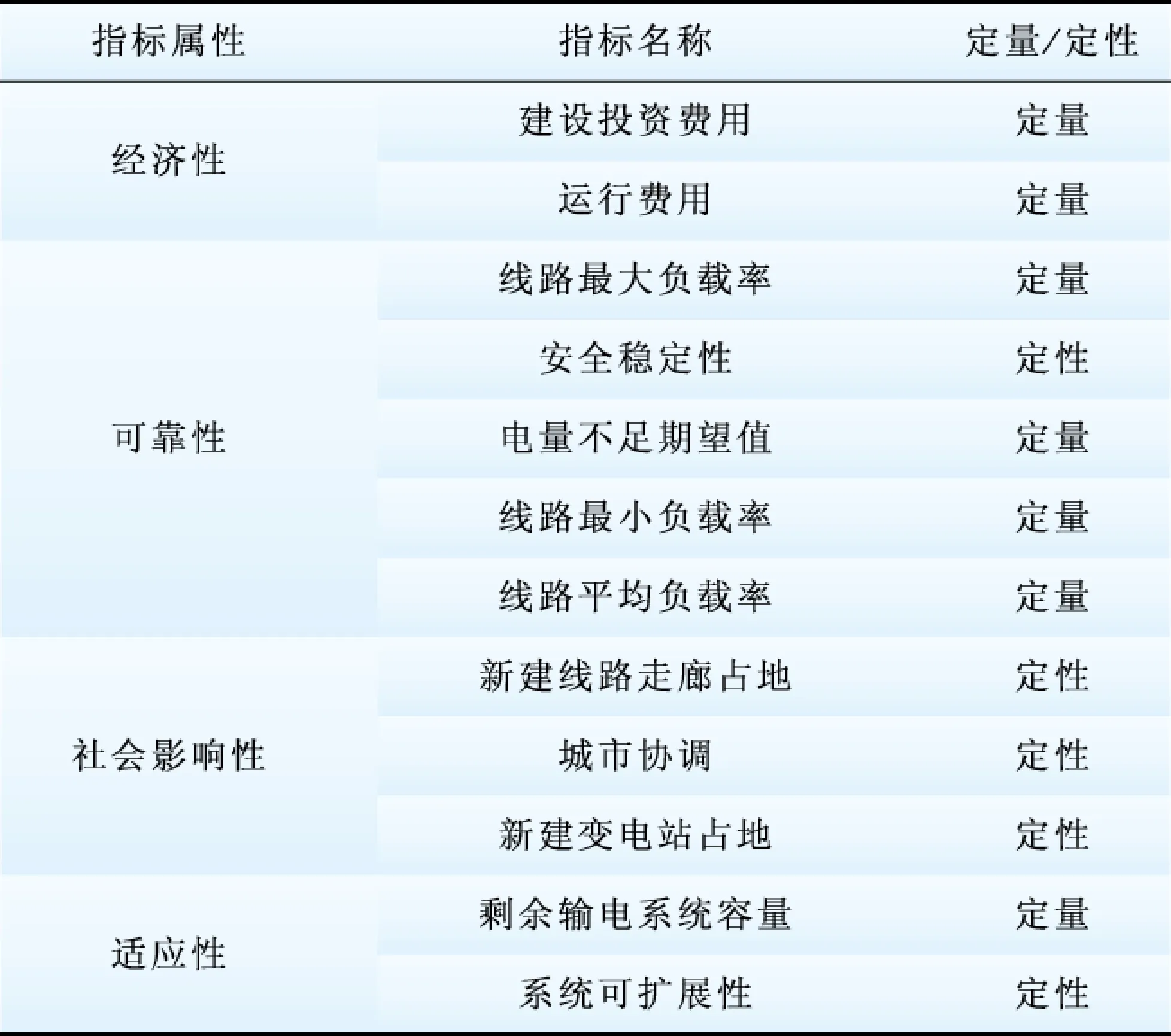
表3 3个方案定量指标数据Table 3 Quantitative index data in three schemes

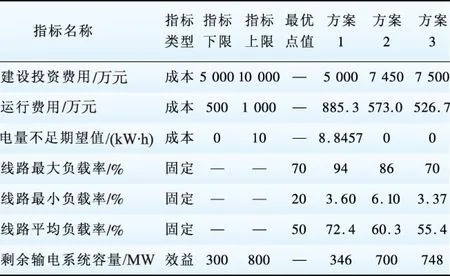
表4 3个方案定量指标归一化结果Table 4 Normalization results of quantitative indices in three schemes

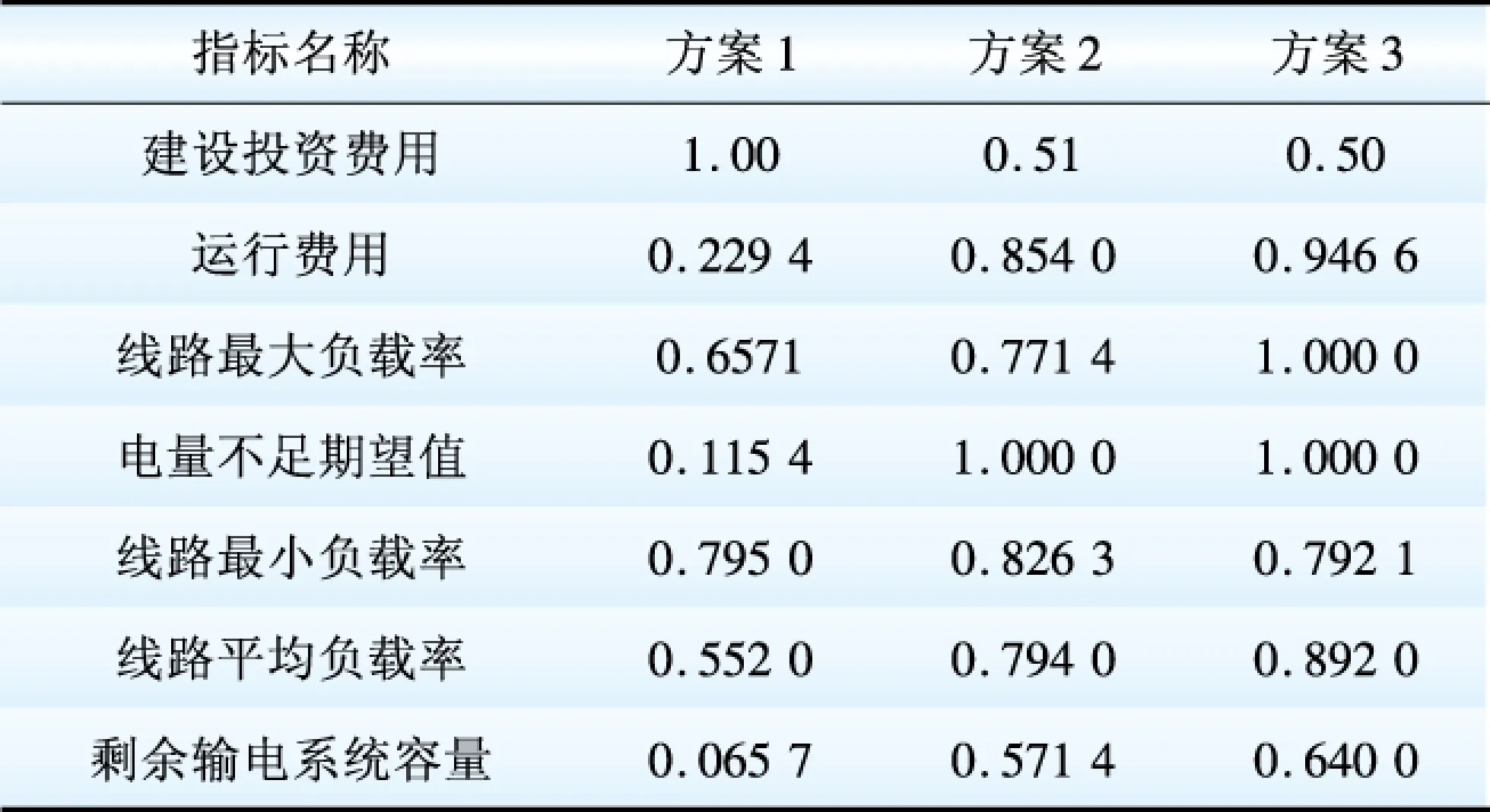
表5 3个方案定性指标专家判断结果Table 5 Expert judgment results of qualitative indices in three schemes

W1= (0.181 3, 0.090 7, 0.083 3, 0.223 9, 0.047 4, 0.042 3, 0.086 2, 0.057 2, 0.010 8, 0.020 2, 0.104 5, 0.052 2)。

表6 3个方案定性指标量化结果

Table 6 Quantitative results of qualitative indices in three schemes

利用序关系法计算得到各指标的权重向量：W2=( 0.144 4, 0.131 3, 0.064 1, 0.083 3, 0.045 8, 0.045 8, 0.064 1, 0.075 7, 0.052 6, 0.063 1, 0.120 3, 0.109 4)。

根据表4和表6各指标的归一化结果，利用熵权法计算得到各指标的权重向量：W3=(0.079 7, 0.086 0, 0.081 2, 0.085 7, 0.086 2, 0.079 8, 0.085 1, 0.084 1, 0.079 7, 0.080 5, 0.086 0, 0.085 8)。

利用变异系数法计算得到各指标的权重向量：W4=( 0.091 6, 0.123 8, 0.046 3, 0.112 6, 0.155 5, 0.005 1, 0.050 4, 0.007 8, 0.021 1, 0.110 9, 0.158 2, 0.116 9)。

根据计算出的4组权重向量由式(5)构造组合权重优化模型，通过粒子群优化算法计算得到各指标的组合权重向量：W=(0.130 5, 0.088 3, 0.088 4, 0.144 2, 0.086 8, 0.054 9, 0.076 0, 0.070 7, 0.045 3, 0.050 4, 0.095 3, 0.069 1)。其中，粒子群求解收敛结果如图3所示，经过几代进化，目标函数值很快收敛到了最小值。随着试验次数增加，可以证实该计算结果真实可信。

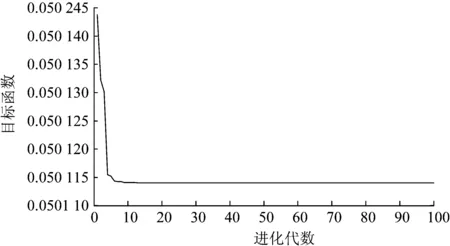
图3 粒子群求解收敛结果Fig.3 Convergence result of PSO

根据本文的12个评价指标的归一化结果和评语的5个等级，由式(6)分别计算3个方案12个评价指标与5种评语等级云模型之间的关联度，得到3个方案的综合评判矩阵D。

基于 各方案的综合评判矩阵D与组合权重向量W，根据式(7)计算得到各方案的综合评判结果向量，如表7所示。

表7 各方案综合评判结果

Table 7 Comprehensive evaluation results vectors of each scheme

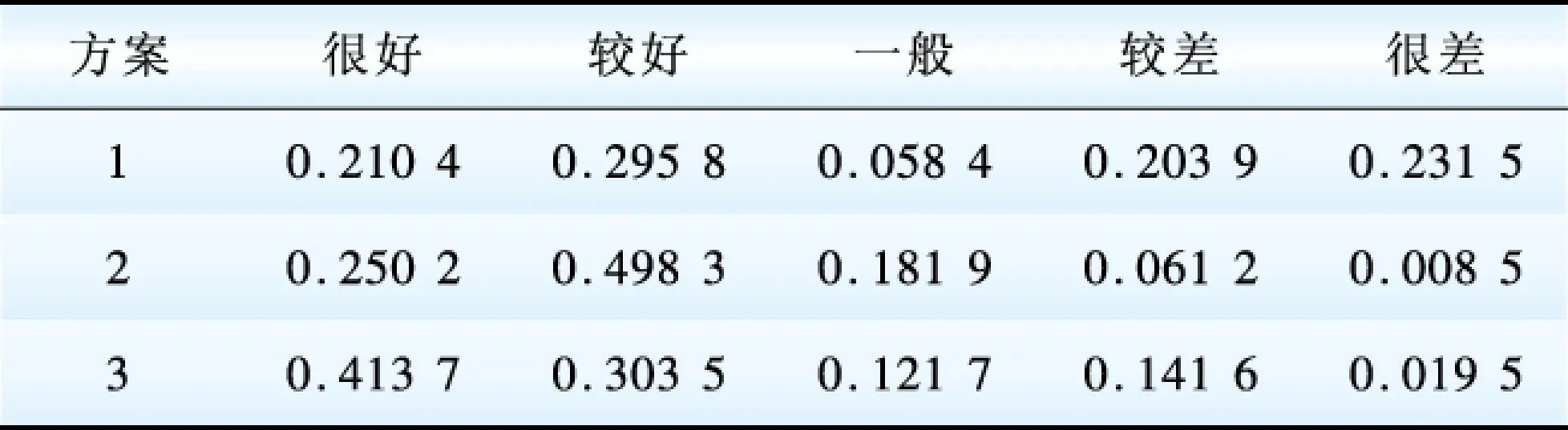
进一步，由式(8)计算得到各方案总评分。方案1为3.049 6；方案2为3.920 5；方案3为 3.950 2。故最终的评价结果：方案3>方案2>方案1，并且方案2与方案3明显优于方案1。与文献[14]的组合权重灰色关联分析、主成分分析法和组合权重Topsis法评价结果比较如表8所示。

表8 仿真结果比较

Table 8 Comparison of simulation results

由表8可知，本文提出的基于组合权重和云模型的评价结果与文献[14]的组合权重灰色关联分析、组合权重主成分分析法和组合权重Topsis法评价结果完全一致。相比之下，本文提出的方法求取的指标权重兼顾了主观赋权与客观赋权的优点，又充分发挥了云模型能反映评价信息的模糊性和随机性的优势，评价过程更为科学全面。

从指标值分析，方案1由于线路负载率较高并且不满足“N-1”安全准则，影响电网的安全稳定运行，因此虽然经济性占优但是评分最低。而方案2和方案3同时满足“N-1”安全准则，方案3的网络充裕度明显优于方案2，可以满足灵活调度以及未来负荷增长的需要，并且考虑到方案2比方案3多1条输电走廊，占地更多。因此从整体考虑，方案3优于方案2。综上所述，可知由基于组合权重和云模型的输电网规划综合决策方法得出的结论合理、可信。

4 结 论

本文将组合权重和云模型相结合应用于输电网规划综合决策中，在层次分析法求取主观权重和熵权法求取客观权重的基础上，利用粒子群优化算法得到评价指标的组合权重，既尊重了专家意见，又充分利用了指标数据信息的客观性；在评价过程中发挥了云模型能充分反映评价信息的模糊性和随机性的优势，提高了综合评价决策结果的科学性和可信度。算例结果表明基于组合权重和云模型的综合评价方法物理意义明晰，易于被规划决策人员掌握，评价结果合理可信，是一种值得推广的方法。

致 谢

本文得到了广东电网规划中心的相关工作人员的大力支持，在此向他(她)们表示衷心的感谢。

[1]程浩忠. 电力系统规划[M]. 北京：中国电力出版社，2008：111-115.

[2]聂宏展，吕盼，乔怡，等. 基于熵权法的输电网规划方案模糊综合评价 [J].电网技术.2009，33(11)：60-64. Nie Hongzhan，Lv Pan，Qiao Yi，et al. Comprehensive decision-making of alternative transmission network planning based on entropy weight method [J].Power System Technology，2009，33(11)：60-64.

[3]刘亚丽. 基于DEAHP方法的输电网规划方案综合评价及决策 [D]. 济南：山东大学，2010. Liu Yali. Comprehensive evaluation and decision-making for tansmission network planning alternatives based on DEAHP method [D]. Shandong University，2010.

[4]聂宏展，聂耸，乔怡，等. 基于主成分分析法的输电网规划方案综合决策[J].电网技术.2010，34(6)：134-138. Nie Hongzhan，Nie Song，Qiao Yi，et al. Comprehensive decision-making of alternative transmission network planning based on principal component analysis [J].Power System Technology，2010，34(6)：134-138.

[5]罗毅，李昱龙. 基于熵权法和灰色关联分析法的输电网规划方案综合决策[J].电网技术. 2013，37(1)：77-81. Luo Yi，Li Yulong. Comprehensive decision-making of alternative transmission network planning based on entropy weight and Grey relational analysis method [J].Power System Technology，2013，37(1)： 77-81.

[6]Li Z H, Lin Y, Chen W H, et al. Fuzzy comprehensive evaluation for transmission grid planning based on combination weight[J]. Power and Energy, 2015: 91.

[7]李德毅，孟海军，史雪梅. 隶属云和隶属云发生器 [J]. 计算机研究与发展， 1995，32(6)：15-20. Li Deyi，Meng Haijun，Shi Xuemei. Membership clouds and membership cloud generators [J]. Computer Research & Development，1995，32(6)：15-20.

[8]李德毅，刘常昱. 论正态云模型的普适性 [J]. 中国工程科学, 2004，6(8)：28-34. Li Deyi，Liu Changyu.Study on the universality of the normal cloud model [J].Engineering Science，2004，6(8)：28-34.

[9]廖良才，范林军，王鹏. 一种基于云理论的组织绩效评估方法 [J]. 系统工程, 2010(1)：99-104. Liao Liangcai，Fan Linjun，Wang Peng. Method of evaluating organizational performance based on cloud theory [J]. Systems Engineering. 2010(1)：99-104.

[10]赵会茹，李娜娜，李天友，等. 基于AHP_云模型配电网故障对象的停电后果评估 [J].华东电力, 2013，41(7)：1456-1460. Zhao Huiru，Li Nana，Li Tianyou，et al. Outage consequence assessment for distribution network failure objects based on AHP cloud model [J]. East China Electric Power, 2013，41(7)：1456-1460.

[11]郭亚军. 综合评价理论、方法及应用 [M]. 北京：科学出版社，2007.

[12]孙凯，鞠晓峰，李煜华. 基于变异系数法的企业孵化器运行绩效评价[J]. 哈尔滨理工大学学报, 2007，(03)： 165-167. Sun Kai，Ju Xiaofeng，Li Yuhua. Performance evaluation of enterprise incubators based on variation coefficient method[J]. Journal of Harbin University of Science and Technology, 2007，(03)：165-167.

[13]Romero R, Monticelli A, Garcia A, et al. Test systems and mathematical models for transmission network expansion planning [J]. IEE Proceedings of Generation Transmission and Distribution. 2002，149(1)：27-36.

[14]李昱龙. 输电网规划方案综合评价方法研究与应用 [D]. 北京： 华北电力大学， 2012. Li Yulong. Application and research on comprehensive assessment modeling method for alternative transmission network planning [D]. North China Electric Power University，2012.

(编辑： 张小飞)

Comprehensive Decision-Making of Transmission Network Planning Schemes Based on Cloud Model

DONG Meiling,YOU Dahai, WANG Gang, CHEN Weihua

(State Key Laboratory of Advanced Electromagnetic Engineering and Technology,Huazhong University of Science and Technology, Wuhan 430074, China)

According to the uncertainty of comprehensive decision-making and the strong subjectivity of index weight determining method in power transmission network planning, a comprehensive decision-making method for transmission network planning schemes was proposed based on the combined weight and cloud model. Firstly, based on the subjective weights calculated by analytic hierarchy process (AHP) and order relation method as well as the objective weights calculated by entropy method and variation coefficient method, the combined weight of each evaluation index was obtained by particle swarm optimization (PSO) algorithm, in order to remedy the insufficiency of experts assigned index weight and objective weight. Then the cloud model was adapted to determine the comprehensive evaluation results of each network planning scheme, which could fully reflect the fuzziness and randomness of index information. Finally, a simulation analysis of IEEE Garver-6 system was given to verify the effectiveness of the proposed decision-making method.

transmission network planning scheme; comprehensive decision-making; combined weight; cloud model; particle swarm optimization algorithm

广东电网公司电网规划研究中心科研项目(030000QQ00120020)。

TM 715

A

1000-7229(2015)10-0154-07

10.3969/j.issn.1000-7229.2015.10.023

2015-07-11

2015-08-28

董美玲(1991)，女，硕士研究生，研究方向为电力系统规划及其综合评价，负荷预测及需求侧管理；

游大海(1957)，男，教授，博士生导师，研究方向为电力系统自动化及电力系统继电保护；

王刚(1990)，男，博士研究生，研究方向为电网规划及其综合评价；

陈伟华(1989)，男，硕士研究生，研究方向为电网规划综合评价，输电网静态稳定，暂态稳定评估等。