考虑暂态稳定约束的最优紧急控制策略

邵常政，丁一，宋永华

(浙江大学电气工程学院，杭州市 310027)



考虑暂态稳定约束的最优紧急控制策略

邵常政，丁一，宋永华

(浙江大学电气工程学院，杭州市 310027)

随着电力市场的深化，用户的可靠性得到重视，为充分体现用户对可靠性的不同要求，将用户的停电成本作为经济性指标，加入优化目标函数作统一优化的紧急控制策略，得到广泛应用。然而，这些决策模型中没有考虑系统的暂态稳定性，这就使得在执行完发电机再调度和切负荷操作后，系统可能无法再次承受故障而不发生暂态失稳。针对这种不足，提出了一种考虑暂态稳定约束的最优紧急控制决策模型，在该模型中加入了表示系统在新的运行点满足暂态稳定的相关约束，因此，发电机再调度以及切负荷等操作完成后，系统仍然能保持暂态稳定性。最后，以IEEE-RBTS的6节点系统和新英格兰39节点系统为算例，对所提出的策略作出具体阐述，并比较该方法与不考虑暂态稳定约束的算法在结果上的差别。

紧急控制；缺电成本；最优模型；电力系统暂态稳定

0 引 言

电力系统的根本任务是以一种经济的方式，为用户持续地供应符合质量要求的电能[1]。稳态时的电力系统往往工作在最优状态，但当系统由于线路或者发电机等元件故障从正常状态过渡到故障状态时，如果发电机的容量不足，则可能需要进行发电机组的再调度或者是切除部分负荷。

适应于传统电力系统体制的切负荷策略已经得到充分发展，这些切负荷策略可以分为2类：(1)基于对系统安全性的考虑[2-4]，这些方法通过潮流等手段分析事故后的系统安全性指标并判断如何切除负荷最能使这些指标恢复到正常水平，以此来指导切负荷操作；(2)基于最优潮流模型[5-6]的策略，这些方法以最小化切负荷量为目标，求解满足网络安全等约束的最优切负荷策略。然而，这2类方法都是从系统的可靠性出发，没有考虑用户对可靠性的不同需求，不符合电力市场情况下用户对可靠性的要求。Goel等提出了一种基于切负荷报价最小的策略，通过不同的切负荷报价，用户对可靠性的不同要求得到了体现[7]。在总结前人工作的基础上， Wang P、 Ding Y等提出了一种基于总成本最小的发电机再调度和切负荷策略，这种方法将用户对可靠性的要求转化为停电成本并和发电成本、备用成本一起构成总的成本函数，并充分考虑了电力市场的运行条件[8]。

通过将用户的切负荷报价或缺电成本加入目标函数中作统一优化，文献[7-8]提出的方法实现了系统最优并充分考虑到了用户对可靠性的需求。然而，在系统进入故障状态，同时发电机再调度、切负荷等操作完成后，系统开始运行在另一个相对稳定的运行点，此时的系统仍然需要满足暂态稳定的要求，这一点文献[7-8]提出的方法不能够完全保证。针对上述不足，本文提出一种考虑故障后系统暂态稳定性的紧急控制策略模型，通过在该模型中加入表示系统暂态稳定性的相关约束保证在新的运行点系统能够承受预想故障而不发生暂态失稳，以此指导发电机再调度和切负荷等操作更能保证系统安全，计算的切负荷结果也更能反映故障的严重程度。

1 数学模型

本文提出的最优紧急控制策略可以构建为一个最优潮流模型，目标函数为系统总的运行成本，包括发电机成本和用户缺电成本。

1.1 目标函数

发生事故时，基于最优潮流的发电机再调度、切负荷策略是一个多目标最优化问题，目标包括降低发电机再调度成本、提高用户可靠性等内容。为了将多目标转化为单目标，需要将用户的可靠性指标转化为经济性指标，即缺电成本。此时目标函数为

(1)

1.2 约束条件

(1)功率平衡约束

(2)

(3)

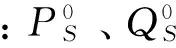
等式(2)、(3)表明在发电机再调度以及切负荷以后，每个节点的输入、输出功率平衡。

(2)发电机出力约束

(4)

(5)

(3)切负荷限制

(6)

(4)电压约束

(7)

(5)线路功率约束

(8)

(6)与暂态稳定性相关的约束

发电机初值方程为

(9)

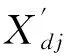
发电机转子运动方程为

(10)

上式是将代表发电机转子运动方程的微分方程差分化的结果。式中：δt(m)、ωt(m)分别为第m个预想故障下某一离散时间点上的发电机转子角度和角速度；ωN发电子额定角速度；Δt为积分步长；Mj和Dj分别为发电机转动惯量和阻尼系数；Pej为发电机的电磁功率。

暂态稳定约束为

(11)

该式表示在任意时刻，各发电机转子偏离惯性中心的角度应在一定范围以内，本文上下限分别取为-100°、100°；惯性中心角度为各发电机转子角度加权平均值，其计算公式为

(12)

式中SG为所有发电机的合集。

本文利用原-对偶内点法进行求解该数学模型，原-对偶内点法是一种求取非线性规划问题的高效算法，能够处理等式约束和不等式约束，并具有良好的收敛性。

2 用户失负荷情况分析

2.1 用户缺电成本

当电力系统由于某一或某些元件故障而从正常状态过渡到事故状态时，如果仅进行发电机再调度无法满足系统平衡的要求，则需要切除部分负荷。缺电成本即可描述为切负荷给用户带来的经济损失，即停电损失。

(1)假设电力系统共有Nc个独立元件，事故状态k下有c个元件故障，状态k的转移率和持续时间分别为

(13)

(14)

图1给出了几种不同负荷类型的停电损失随停电时间变化的曲线[11]。

图1 不同负荷类型用户停电损失曲线Fig.1 Customer power outage cost curves with different loads

2.2 用户失负荷期望

为综合体现某一事故状态的概率以及该状态下用户的失负荷量，本文引入失负荷期望值ELS，相关计算公式如下。

(1)假设电力系统共有Nc个独立元件，事故状态k下有c个元件故障，则状态k的概率为

(15)

式中：Uc为第c个元件故障的概率；Ac则为第c个元件处于正常状态的概率[11]。

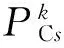
(16)

式中SDi为i节点上所有负荷种类的集合。

3 算例分析

本文选取RBTS6节点系统作为仿真系统，并对部分发电机出力上限进行调整，RBTS6节点系统的单线图及部分数据如图2[12]所示。

图2 RBTS系统单线图Fig.2 Line diagram of RBTS

本文假设线路1发生故障后的状态为状态1，分析该状态下的最优发电机再调度和切负荷策略，并计算各节点的失负荷期望值。同时，将本提出的算法同不考虑暂态稳定约束的方法进行比较，并简单造成差异的原因。

3.1 运行结果

将不考虑暂态稳定约束的情况作为Case1，考虑暂态稳定约束的情况作为Case2，相关数据如下。

(1)发电机再调度结果如表1所示。

(2)切负荷结果如表2所示。

3.2 原因分析

比较Case1和Case2结果的差别，可以看出两者计算结果的区别体现在发电机出力上的不同以及由之引起的各节点切负荷量的不同。造成这种差别的原因为：本文提出算法即Case2，考虑了系统暂态约束，因此部分发电机的出力受到限制，导致系统切负荷量发生变化。

具体地说，在本文采用的算法中，发电机6～11的出力受到限制。图3给出了本文算法中，母线1和母线2上各发电机转子摇摆曲线，观察发电机转子摇摆曲线可以发现，母线2上的6～11发电机转子角度相对惯性中心的角度趋于极限值100o。这说明暂态稳定约束起到了约束发电机转子运动的作用，而如果不加入暂态稳定约束，当预想故障集中的故障发生后，6～11发电机转子相对惯性中心角度将超出极限值，发生暂态失稳，如图4所示。

表1 再调度后的发电机出力

Table 1 Generator output after re-scheduling

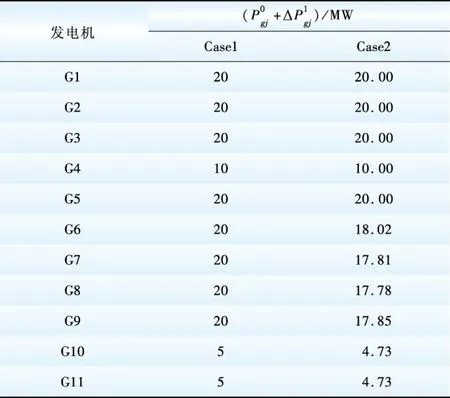
表2 各节点失负荷期望值Table 2 ELS of each node

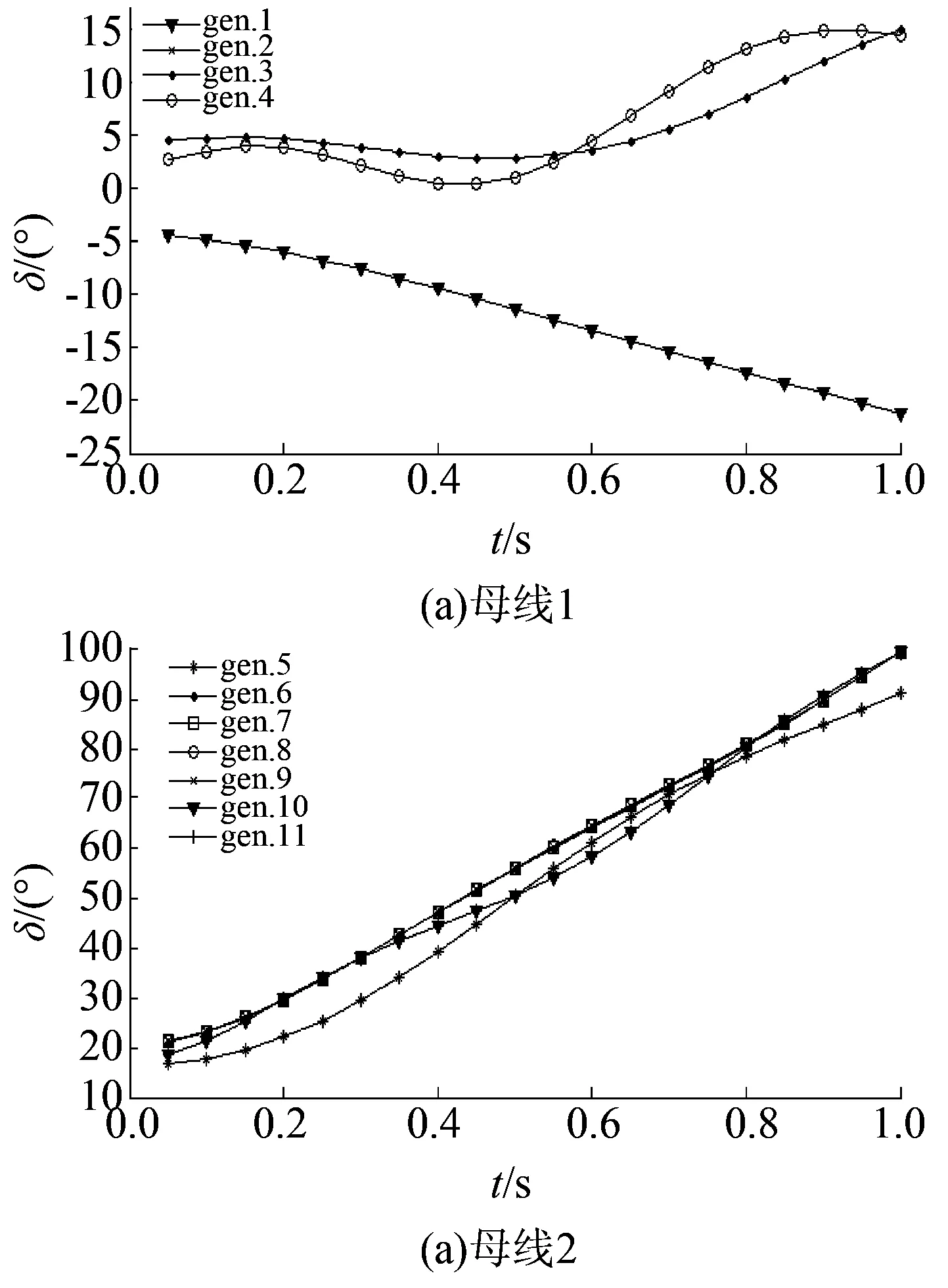
图3 发电机转子运动曲线Fig.3 Motion curves of generator rotors

在线路1发生故障系统进入状态1时，电力系统的运行条件变差，系统再次发生故障的概率也随之增加，为了保证系统安全运行，在发电机再调度和切负荷操作中，有必要考虑系统在状态1下的暂态稳定性。因此，本文在提出的最优切负荷策略中考虑系统暂态稳定约束是有必要的。

图4 6～11发电机转子运动曲线Fig.4 Motion curves of No.6-11 generator rotors

3.3 算例2计算结果

为增强说服力，本文同时对新英格兰39节点数据进行仿真，当线路5发生故障后，考虑暂态稳定约束和不考虑暂态稳定约束的各节点失负荷期望值见图5。

图5 各节点失负荷期望值数据Fig.5 ELS of each node

由图5可以看出，考虑暂态稳定约束的情况下，多数节点失负荷期望值会增加，系统总体失负荷情况也更加严重，计算结果进一步支撑了本文的观点。

4 结 论

当由于元件故障，系统从正常状态转变为事故状态时，为满足系统功率平衡和网络安全约束，有时需要进行切负荷操作。而电力市场的发展要求在进行切负荷操作时充分考虑用户的不同需求，即对于相同的失负荷量，用户的经济损失可能不同。因此，本文提出的切负荷策略将用户的停电成本作为目标函数的一部分构建最优潮流模型并进行求解以获得综合成本最小的切负荷操作。

在系统由于元件故障而转变为事故状态，同时发电机再调度、切负荷等操作完成后，系统开始运行在另一个相对稳定的运行点，此时系统仍然需要能够承受预想故障而不发生暂态失稳，为此本文在最优切负荷模型中加入了表示系统在新的运行点满足暂态稳定的相关约束。

由于考虑了暂态稳定约束，系统的解算规模急剧扩大，针对此类问题，已有文章提出新的高效的算法[13-14]，应用这些方法将极大地提高计算效率，使得本文提出的考虑暂态稳定约束的最优切负荷策略具有现实可行性。

[1]赵渊,周家启,周念成，等.大电力系统可靠性评估的解析计算模型 [J].中国电机工程学报,2006,26(5):19-25. Zhao Yuan, Zhou Jiaqi, Zhou Niancheng, et al. An analytical approach for bulk power systems reliability assessment[J]. Proceedings of the Chinese Society for Electrical Engineering, 2006,26(5):19-25.

[2]李山,江北平,蒋东荣.基于最小负荷裕度计算方法的最优切负荷算法[J].重庆理工大学学报：自然科学，2011,6,25(6):29-32. Li Shan, Jiang Beiping, Jiang Dongrong. Optimal load-shedding algorithm based on minimum load margin calculation approach[J]. Journal of Chongqing University of Technology：Natural Science, 2011,6,25(6):29-32.

[3]李卫星,牟晓明,孙勇.基于解析灵敏度的低压切负荷优化控制方法[J].中国电机工程学报,2013,10,33(28):67-73. Li Weixing, Mou Xiaoming, Sun Yong. An undervoltage load shedding method based on analytical sensitivity[J]. Proceedings of the CSEE, 2013,10,33(28):67-73.

[4]王菲,余贻鑫,刘艳丽.基于安全域的电网最小切负荷计算方法[J].中国电机工程学报,2010,5,30(13):28-33. Wang Fei, Yu Yixing, Liu Yanli.Minimum load-shedding calculation approach based on the security region in the power grid[J]. Proceedings of the CSEE, 2010,5,30(13):28-33.

[5]Billinton R, Khan E. A Security based approach to composite power system reliability evaluation[J]. IEEE Transaction on Power System, 1992, 7(1):65-72.

[6]Meio A C G, Mello J C O, Granville S. The effects of voltage collapse problems in the reliability evaluation of composite systems[J]. IEEE Transaction on Power System, 1997, 12(1):480-488.

[7]Goel L, Aparna V P, Wang P. A framework to implement supply and demand side contingency management in reliability assessment of restructured power systems[J]. IEEE Transaction on Power System, 2007, 22 (1):205-212.

[8]Wang P, Ding Y, Goel L. Reliability assessment of restructured power system using optimal load shedding technique[J]. IET Generation, Transmission & Distribution, 2009, 3(7) :628-640. [9]韦化,阳育德,李啸骢. 多预想故障暂态稳定约束最优潮流[J].中国电机工程学报,2004,24(10):91-96. Wei Hua, Yang Yude, Li Xiaocong. Optimal power flow with multi-contigencies transient stability constrained[J]. Proceedings of the CSEE, 2004,24(10):91-96.

[10]Billinton R, Allan R N. Reliability evaluation of power systems[M]. New York, US: Springer US, 1996:443-475.

[11]Billinton R, Allan R N. Reliability assessment of large electric power systems[M]. Massachusetts,US:Kluwer Academic Publishers, 1988:183-228.

[12]Billinton R, Kumar S, Chowdhury N, et al. A reliability test system for education purposes-basic data[J]. IEEE Transaction on Power System, 1989,4(3):1238:1244.

[13]Tu Xiaoping, Dessaint L A, Kamwa I. Fast approach for transient stability constrained optimal power flow based on dynamic reduction method[J]. IET Generation Transmission & Distribution, 2013, 8(7):1293-1305.

[14]阳育德,韦化,李滨. 求解暂态稳定约束最优潮流模型的递推降阶解耦算法[J]. 中国电机工程学报,2015,35(2):335-343. Yang Yude, Wei Hua, Li Bin. Recursive and decoupling approach for solving transient stability constraints optimal power flow[J]. Proceedings of the CSEE, 2015,35(2):335-343.

宋永华(1964), 男，教授，博士，研究方向为电力市场，电力系统运行。

(编辑：蒋毅恒)

Optimal Emergency Control Strategy Considering Transient Stability Constrains

SHAO Changzheng, DING Yi, SONG Yonghua

(College of Electrical Engineering, Zhejiang University, Hangzhou 310027, China)

With the deepening of the power market, the user’s reliability has been paid much attention. In order to fully reflect the different reliability requirements of users, the emergency control strategies which take the power outage cost of users as economic index in optimization objective function have been widely used. However, these decision models do not consider the transient stability of the system, so the system may be unable to withstand failure again and cause transient instability after the execution of generator re-scheduling and load shedding. In view of this problem, this paper proposed an optimal emergency control strategy with considering transient stability constrains. The relevant constraints were used in this model could indicate that the system satisfied the transient stability at the new operating point. Therefore, the system could still maintain transient stability after the execution of generator re-scheduling and load shedding. Finally, taking IEEE-RBTS 6-nodes system and new-England 39-nodes system as example, the proposed strategy was described in detail, and its result was compared with that of the strategy without considering transient stability constrains.

emergency control; power outage cost; optimal model; transient stability of power system

中国电力科学研究院科技项目(epri4110-150627)。

TM 715

A

1000-7229(2015)10-0118-05

10.3969/j.issn.1000-7229.2015.10.018

2015-07-06

2015-09-11

邵常政(1992)，男，博士生，研究方向为电力市场；

丁一(1978)，男，教授，博士，研究方向为电力市场，电力系统可靠性；