基于改进Logistic模型阶段划分理论的饱和负荷预测

张帆，刘杰锋，李冰，陈纲亮，季节，徐康泰

(国网冀北电力有限公司经济技术研究院，北京市 100045)



基于改进Logistic模型阶段划分理论的饱和负荷预测

张帆，刘杰锋，李冰，陈纲亮，季节，徐康泰

(国网冀北电力有限公司经济技术研究院，北京市 100045)

用电需求的饱和负荷预测可以确定一个地区未来电网发展与用电需求的最终规模，并以其远期电网规划目标指导近期电网建设，可以有效减少电网改造成本，做到有步骤有条理地进行该地区区域电网的改造与建设，对区域规划、区域经济与电网之间的协调发展具有重要意义。该文提出了基于改进Logistic模型的负荷发展历程阶段划分理论，并给出了饱和负荷的新内涵，修正与完善了判定电力饱和负荷的量化指标体系。最后采用改进Logistic模型对案例进行了研究与分析，完成了案例用电饱和规模以及饱和时间点的预测与分析工作，并验证了其可行性。

饱和负荷；阶段划分理论；量化的指标体系；改进Logistic模型

0 引 言

从发达国家的电力发展历史来看，电网的发展由于受到土地、交通、环境、自然资源及政策等因素的制约，会随着社会经济和电力基础设施的建设趋于稳定而最终趋于饱和[1]。在我国由于经济发展存在城乡差异、地域差异，区域经济发展存在很大的不平衡性[2]。一些经济发达地区，经济发展速度开始放缓，电力需求增长速度也开始降低，其电力负荷增长开始呈现出饱和趋势。这些经济发达地区在进行中长期电网规划时需要考虑电网发展的最终规模，也需要考虑电网饱和负荷的规模以及到来的可能时间，从而指导城市电网的建设和改造，饱和负荷的概念应运而生。

目前，对于饱和负荷的研究大多数是针对城市饱和负荷[3]，对于区域级饱和负荷研究较少，而且对饱和负荷的概念也没有明确、统一的定义。

文献[4-5]采用logistic曲线对城市电力饱和负荷进行分析预测。文献[6]结合城市发展规划，分别采用人均用电量法和负荷密度法对天津市中心城区用电需求饱和状况进行了预测。文献[7]对饱和负荷阶段城市的经济、社会特点进行了研究与总结，提出了适用于城市的宏观、微观饱和负荷预测的方法，而且采用闭环校验法检测了其预测结果。文献[8]采用基于人均用电量与人均用电负荷的饱和负荷预测方法对华东某一小城市的全社会用电量与用电负荷的饱和规模与饱和时间进行了预测。文献[9]采用基于影响因素分析的多维度饱和负荷预测方法，建立了以影响因素为自变量、电力或电量需求为因变量的数学模型，该方法可以确定影响因素在其所在点的变动对电力或电量需求带来的冲击或影响，从而可以对影响因素作灵敏度分析，弥补了时间序列法负荷预测的不足，具有比较高的预测精度，也有着一定的创新性，对饱和负荷预测具有一定的指导意义。文献[10-11]介绍了系统动力学建模方法及其在饱和负荷预测中的应用。[12-14]介绍了神经网络模型在中长期负荷预测中的应用。

本文主要对传统的Logistic模型进行改进，使其能够更好地适用于中长期电力负荷预测；提出基于改进Logistic模型的负荷发展历程阶段划分理论，明确判断电力负荷所处的发展阶段；提出饱和负荷发展的新内涵，使其更好地对电力饱和负荷的概念进行阐述；修正与完善判定电力饱和负荷的量化指标体系，使其能够更好地为我国城市、区域电力饱和负荷的判定提供依据。最后采用改进Logistic模型对案例进行研究与分析，明确该案例电力负荷所处的发展阶段，完成其用电饱和规模以及饱和时间点的预测与分析工作，并验证其正确性与可行性。

1 传统Logistic模型

Logistic曲线是一种最常用的“S”型曲线模型。该模型首先源于对生物种群的研究，通过大量的科学观察研究，发现经济、社会、人口以及科技领域中很多事物的成长过程，以及事物成长过程中的某个或某些定量化特性也符合生物成长过程中的曲线规律。传统的Logistic模型是比利时数学家P. Fvehulst于1938年提出的，又被称为自我抑制性方程，该曲线模型的方程如下。

(1)

图1 饱和增长logistic曲线Fig.1 Logistic curve for saturated load

2 改进Logistic模型

通过实际研究表明，传统的Logistic曲线模型收敛性比较差，而且缺少对随机变量影响的考虑，因此往往会影响其拟合与预测精度。所以本文对Logistic曲线模型进行了改进，考虑了随机变量的影响，具体操作是对传统的Logistic数学模型增加了一个随机变量c，该随机变量会随着具体的原始数据的拟合情况而自动改变与调整。另外，如果预测模型可变参数太少，则模型自由度低，拟合效果可能很差；扩展模型可变参数数目，可增加模型自由度，提高参数估计效果和历史数据拟合精度[15]，其改进后的模型为

(2)

其中k>0，a>0，b<0，c为常数，这样的模型其基本形状与性质不变，但可以很好地改善与增加预测的精度与水平。

3 基于改进Logistic模型的负荷阶段划分理论

对改进Logistic曲线数学模型式(2)求一阶导数：

(3)

由于k>0，a>0，b<0，c为常数，从而可以判断该一阶导数恒为正，所以yt为关于t的单调递增函数。

对式(2)求二阶导数可知其导数为

(4)

(5)

对式(2)求三阶导数可得：

(6)

令式(6)为0可知其有2个零点(T1，y1)与(T3，y3)，从而有：

(7)

通过上述分析，得到了3个时间节点，可以按照这些时间点来划分Logistic函数，具体如下：

y(t)求到三阶导时，可得到其时间特征点为T1、T2、T3。结合图2以及改进Logistic函数本身的特点，可以将其发展阶段划分为：0—T1初期增长发展阶段，T1—T2快速增长发展阶段，T2—T3后期快速增长发展阶段，T3—∞对应的这一时间段为饱和增长发展阶段。

当采用改进Logistic函数进行电力发展阶段拟合与划分时，可以分别按全社会用电量与电力负荷2种方式来进行划分与研究，从而可以按照各自的实际发展情况来确定其时间特征点。最后可以用2种方式的时间特征点进行对照研究与分析，一方面可以验证该划分理论的科学性与合理性，另一方面可以对照2种方式的时间特征点确定共同适用的时间特征点，从而有助于分析出最合理的电力发展划分阶段。

图2 Logistic曲线的4阶段划分理论Fig.2 Four stages division theory of Logistic curve

4 电力需求达到饱和的判定指标体系

借鉴研究发达国家和地区的经济社会与电力负荷发展规律和发展历程，本文结合我国国情以及某区域电网用电情况修改完善了电力需求进入饱和阶段的判定条件。

用电量增长率、最大负荷增长率、人均用电量指标是判定一个地区电力负荷是否进入饱和阶段的必要性条件指标。当一个城市或区域经济发展与电力负荷进入饱和时期时，其用电量与年最大负荷持续增长率的绝对值一般情况下将低于2%[16]，但由于个别年份经济异常或者其他突然事件或政策因素导致出离这一范围也应酌情予以考虑；另外，还应满足表1中包括人均用电量、人口变化率、人均GDP、产业结构指标在内的其他一些指标。通过这些指标可判定所研究城市、区域的电力系统负荷是否进入了饱和发展时期。

5 饱和负荷发展的新内涵

以往一些研究资料认为只要电量、负荷的增长率小于2%即可认为是该电量或负荷已经达到了饱和[17-18]，虽然这对饱和负荷预测工作具有一定的指导价值，但这样一个判据与结论也不能揭示饱和负荷的真正内涵，需要进一步综合研究与探讨。接下来将对饱和负荷新的内涵进行研究与探讨。

表1 电力需求进入饱和阶段的判定条件

Table 1 Judging condition of Power demand into saturation stage

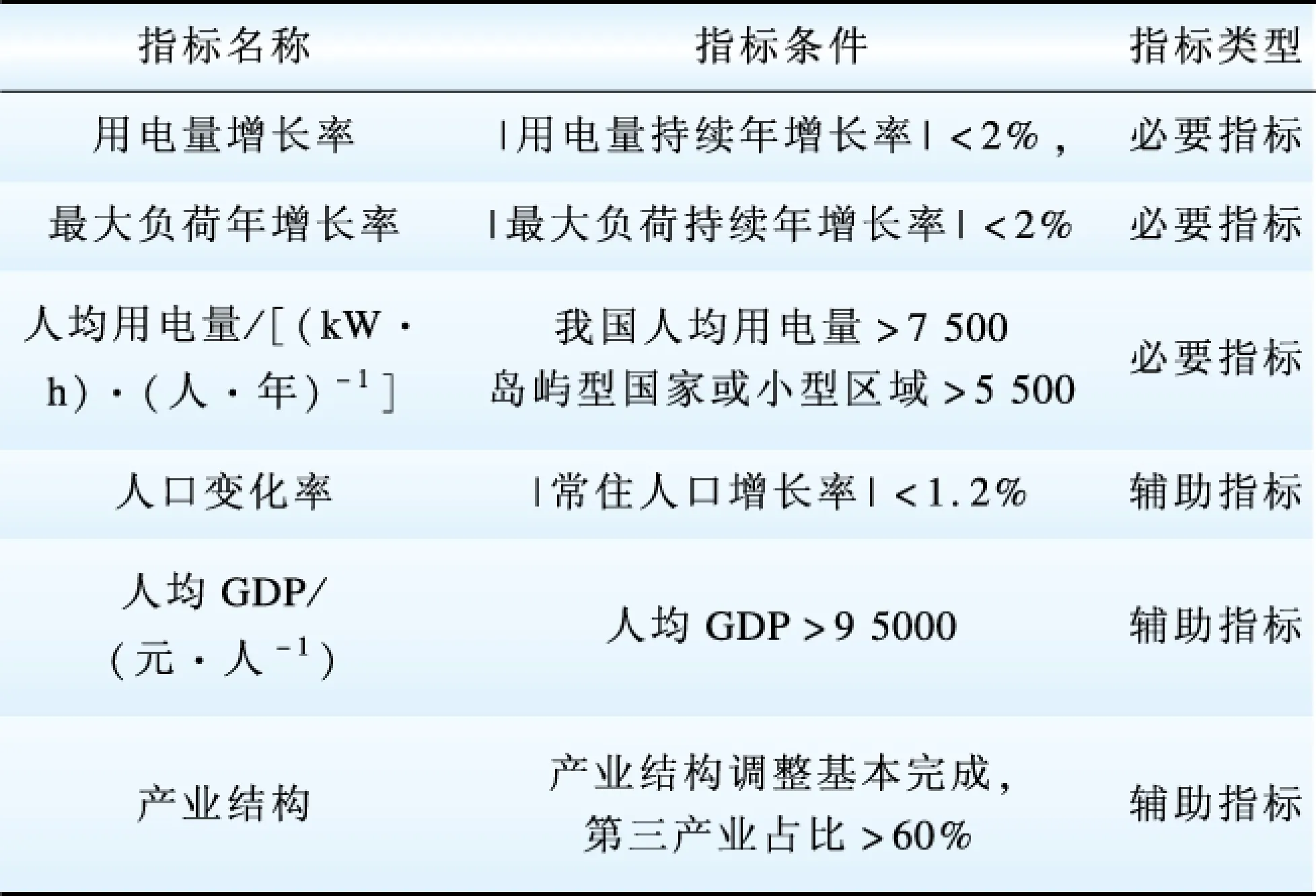
结合本文基于Logistic曲线饱和负荷发展阶段划分理论的研究，并通过对华东区域饱和负荷发展状况的研究，表明当电量或负荷的增长率小于3～4%的时候认为该区域电力工业已经进入饱和发展阶段。但饱和发展阶段并不是真正意义上的饱和阶段，其对应的值也不是真正意义上的饱和值，即便以1.9%的增长速度一直增长10年，其10年后的值将比初期参考值增长了接近20.7%之多，那么这势必给饱和负荷最终规模的评定带来争议，也对饱和负荷最终规模与饱和负荷到达时间预测的准确性带来冲击，从而影响饱和负荷预测的准确程度与意义，也给未来电力规划的准确性与合理性带来影响。真正意义上的饱和值，除了需要符合本文提出的电力需求进入饱和阶段的判定指标体系外，更重要的是数值上不再有大的变化，但可以出现一定的波动裕度与区间，在这样的波动裕度与区间内我们即可认为是真正意义上的饱和值。这便是本文所提出的饱和负荷定义和新的内涵。

6 案例分析

6.1 改进Logistic模型对案例的拟合预测及精度评价

案例所选取的分析数据是某省历史上的全社会用电量与负荷数据，如表2所示。

根据表2所提供的数据，采用改进Logistic曲线模型分别对该省的全社会用电量和用电负荷进行拟合与预测，得到全社会用电量的拟合预测曲线如图3所示，得到用电负荷的拟合预测曲线如图4所示。

用改进Logistic曲线模型分别对该省全社会用电量和用电负荷进行拟合预测，部分数据如表3所示，对其建模精度进行分析与评价。

表2 某省的用电量、负荷数据

Table 2 Electricity consumption and load data of a certain province

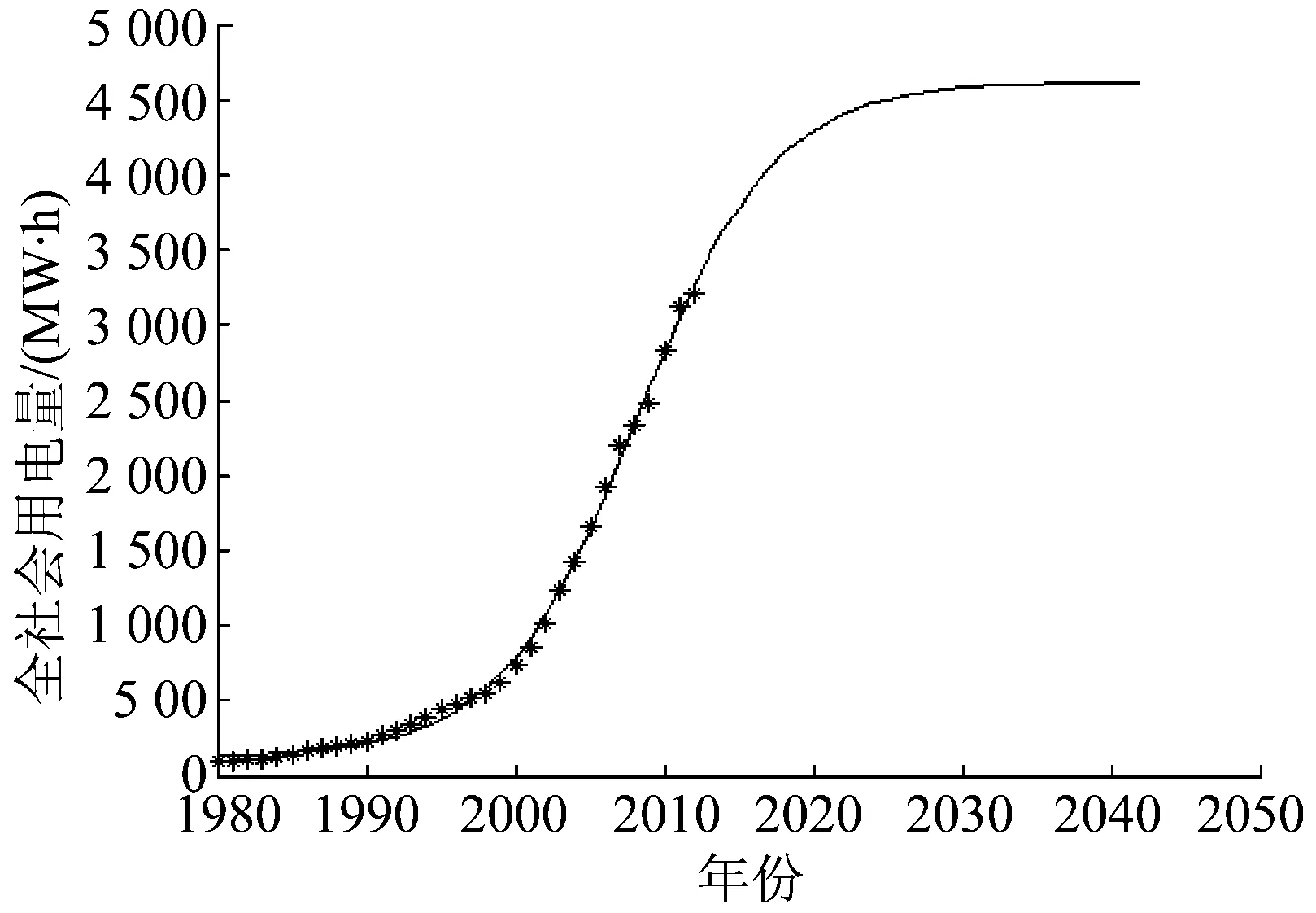
图3 改进Logistic模型对某省用电量预测Fig.3 Electricity demand forecasting of a certain province by improved Logistic model

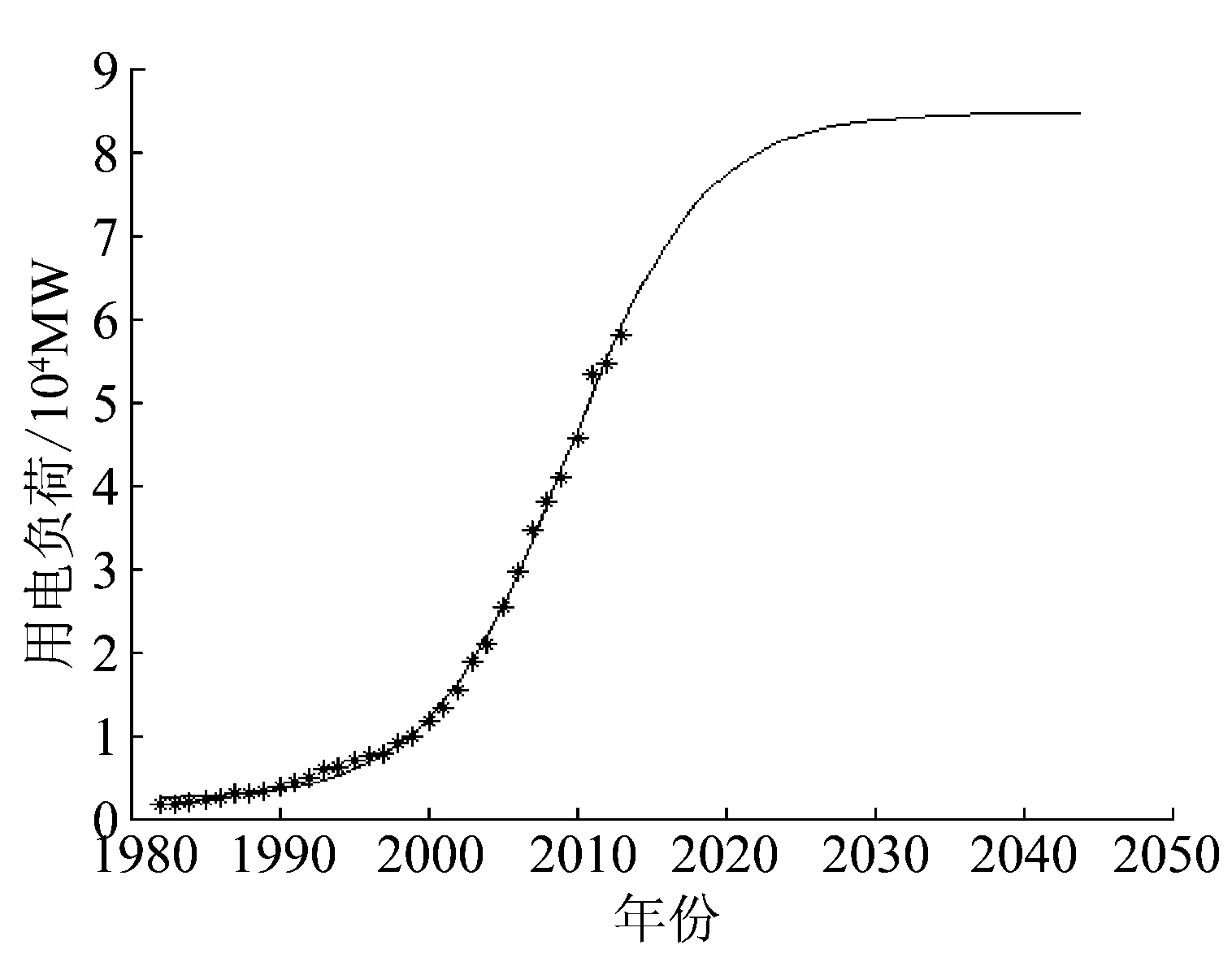
图4 改进Logistic模型对某省用电负荷预测Fig.4 Power load forecasting of a certain province by improved Logistic model表3 改进Logistic模型拟合预测结果Table 3 Fitting and forecasting results of improved Logistic model

(8)

可见改进Logistic模型对该省全社会用电量的预测有着比较高的建模精度。

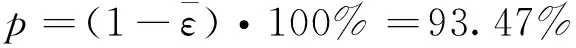
(9)

可见改进Logistic模型对该省年最大负荷的预测也有着比较高的建模精度。

6.2 改进Logistic模型对案例的负荷阶段划分

根据图3改进Logistic模型对全社会用电量的拟合预测结果，基于本文改进Logistic模型的饱和负荷阶段划分理论来进行研究与阶段划分，可以得到T1=2002.03、T2=2008.14、T3=2014.25，可以认为T1为2002年、T2为2008年、T3为2014年，所以可以认为2002年之前该省电力发展处于初始增长阶段、2002年到2008年处于电力快速增长阶段，2008年到2014年增长速度有所减缓，进入后发展阶段，2014年之后该省电力发展步入饱和发展阶段。

同理，根据图4对该省年最大负荷的拟合预测结果，可以得到T1=2003.26、T2=2009.34、T3=2015.43，可以认为T1为2003年、T2为2009年、T3为2015年，所以可以认为2003年之前该省电力发展处于初始增长阶段、2003年到2009年处于电力快速增长阶段，2009年到2015年增长速度有所减缓，进入后发展阶段，2015年之后该省电力发展步入饱和发展阶段。

通过分析用电量和用电负荷可知，两者有着极大的相似性。两者的T1、T2、T3各相差了1年，也就是负荷分析比用电量分析阶段划分对应年份仅仅晚了1年，二者T1与T2、T2与T3之间各相差了6年，这是完全一致的，进而证明了电力负荷Logistic模型阶段划分理论的正确性与有效性。

6.3 改进Logistic模型对案例的饱和负荷预测

选取预测年份2010、2015、2020、2025、2030与2035年，由该省对应年份全社会用电量的数据以及最大负荷的数据如表4所示。结合案例预测具体数据进行分析，该省从2035年开始，其用电量、负荷增长速度就变得很小，从2035年开始其用电量与负荷就基本稳定而不再增长。所以可以认为该省用电量、负荷达到饱和的年份是2035年，其全社会用电量的饱和值为4 604.1亿kW·h，负荷的饱和值为84 380.1 MW，由此可得其最大负荷利用小时数为5 456.3 h，对该省来说是一个合理的值，从而可以佐证二者关系的准确性。最大负荷利用小时数整体也呈现递减趋势，这与对发达国家的研究状况一致。

表4 改进Logistic模型饱和负荷预测结果

Table 4 Saturated load forecasting results of improved Logistic model

7 结 论

(1)对传统Logistic模型进行了改进，增加了模型对随机变量的考虑，从而增加了模型自由度，提高了参数估计效果和历史数据拟合精度使其能够更好地适用于中长期电力负荷预测以及饱和负荷预测。

(2)提出了基于改进Logistic模型的负荷阶段划分理论，通过对Logistic曲线方程3次求导而获得3个关键的时间节点，从而将电力发展划分为4个阶段，即初期增长发展阶段、快速增长发展阶段、后期快速增长发展阶段与饱和增长发展阶段。

(3)对电力需求达到饱和的判定指标体系进行了完善并提出了饱和负荷发展的新内涵，从而使其能更好地为饱和负荷的预测和判定工作服务，对饱和负荷预测工作具有一定的指导意义。

(4)饱和负荷的预测是一项长期而艰巨的工作，只有不断更新用电需求以及社会经济发展的相关数据，并根据获取的最新数据对未来用电需求进行滚动预测与修正，方能得到更加科学、准确、合理的预测结果。

[1]Elders I M, Ault G W, Galloway S. Identification of long-term scenarios of electricity network development [C]// International Conference on Future Power Systems，Amsterdam，2005.

[2]崔凯，李敬如，刘海波，等城市饱和负荷阶段电力规划方法及其在济南电网中的应用[J].电网技术，2007，31(S2):14. Cui Kai, Li Jingru, Zhao Biao, et al.Power planning method in city Saturated load stage and its application to Jinan power grid)[J]. Power System Technology，2007，31(S2)：14.

[3]肖欣，周渝慧，张宁，等.城市电力饱和负荷分析技术及其应用研究综述[J].电力自动化设备，2014，34(6)：146-152. Xiao Xin, Zhou Yuhui, Zhang Ning, et al. Survey of saturated load analysis technology for urban power system and its application[J]. Electric Power Automation Equipment, 2014，34(6)：146-152. [4]Jia Y, Li S, Tan Y, et al.Improved parametric estamation of logistic model for saturated load forecast[C]//Power and Energy Engineering Conference，Shanghai，China，2012.

[5]肖峻，杜柏均，耿芳.城市电力负荷饱和分析方法 [J].电力科学与技术学报，2009，24(4)：54-58. Xiao Jun, Du Bojun, Geng Fang. Analysis method of city saturated load[J]. Proceedings of Power Science and Technology, 2009，24(4)：54-58.

[6]崔凯，张丽娟，李敬如，等.天津市中心城区饱和负荷分析与预测[J].电力技术经济，2008，20(5)：33-36. Cui Kai, Zhang Lijuan, Li Jingru, et al. Analysis and forecast of saturated load for the central city district of Tianjin[J]. Electric Power Technologic Economics, 2008, 20(5): 33-36.

[7]崔凯，李敬如，赵彪，等.城市饱和负荷及其预测方法研究[J].电力技术经济，2008，20(6)：34-38. Cui Kai, Li Jingru, Zhao Biao, et al. Research on city saturated load and its forecast methods[J]. Electric Power Technologic Economics, 2008, 20(6)：34-38.

[8]张建平，刘杰锋，陈屹东，等.基于人均用电量和人均用电负荷的饱和负荷预测[J].华东电力，2014，42(4)：0661-0664. Zhang Jianping，Liu Jiefeng，Chen Yidong， et al. Saturated load forecasting based on per capita electricity consumption and per capita electricity load[J].East China Electric Power，2014，42(4)：0661-0664.

[9]刘杰锋，程浩忠，韩新阳，等.多维度饱和负荷预测方法及其应用[J].电力系统及其自动化学报，2015，27(2)：44-50.

Liu Jiefeng，Cheng Haozhong，Han Xinyang et al. Multi-dimensional saturated load forecasting method and its application [J].Proceedings of the CSU-EPSA，2015，27(2)：44-50.

[10]Maiorano A, Song Y H, Trovato M. Dynamics of non-collusive oligopolistic electricity markets[C]//Power Engineering Society Winter Meeting, IEEE, 2000(2): 838-844. [11]Yang H M，Wang G J，Zhou L X.A study of power market dynamics based on system dynamics modeling[C]//International Conference on Power System Technology，Chongqing，China：IEEE, 2006：1-6.

[12]Abou A A，El-zaftawy A A，Allam S M，et al.Long-term load forecasting and economical operation of wind farms for Egyptian electrical network[J].Electric Power Systems Research，2009，79(7)：1032-1037.

[13]Kandil M S，El-Debeiky S M，Hasanien N E.Long-term load forecasting for fast developing utility using a knowledge-based expert system[J].IEEE Transaction on Power Systems，2002，17(2)：491-496.

[14]Barbounis T G，Theocharis J B，Alexiadis M C，et al.Long-term wind speed and power forecasting using local recurrent neural network models[J].IEEE Transaction on Energy Convertion，2006，21(1)：273-284.

[15]宁波，康重庆，夏清.中长期负荷预测模型的扩展策略[J]. 中国电力, 2000，33(10)：36-38，108. Ning Bo, Kang Chongqing, Xia Qing. The expansion strategy for medium and long term load forecasting model[J]. Electric Power, 2000，33(10)：36-38，108.

[16]Jia Y D，Li S H，Tan Y，et al.Improved parametric estamation of logistic model for saturated load forecast [C]//Power and Energy Engineering Conference，Shanghai：IEEE, 2012：1-4. [17]王伟，房婷婷.人均用电量法在区域饱和负荷预测中的应用研究 [J].电力需求侧管理，2012，20(6)：34-38. Wang Wei，Fang Tingting. The application of per person electricity consumption method in saturation load forecasting[J]. Power Demand Side Management, 2012，20(6)：34-38.

[18]王芳东，林韩，李传栋，等.基于经济曲线饱和态势分析的饱和负荷宏观预测研究 [J].华东电力，2010，38(10)：1486-1491. Wang Fangdong，Lin Han，Li Weidong，et al. Research on saturated load macroscopically forecast based on saturated situation analysis of economy curve[J]. East China Electric Power, 2010，38(10)：1486-1491.

(编辑： 张小飞)

Saturated Load Forecasting Based on Stages Division Theory of Improved Logistic Model

ZHANG Fan，LIU Jiefeng, LI Bing，CHEN Gangliang, JI Jie，XU Kangtai

(State Grid Jibei Eclectic Power Company Limited Economic Research Institute, Beijing 100045, China)

The saturated load forecasting of power demand can determine the ultimate size of a region’s future grid development and power demand, and the forward power grid planning goals can be used to guide recent grid construction, which can effectively reduce the cost of the reconstruction of power grid, contribute to the work of gradual and methodical renovation and construction of the regional power grid, and has great significance for the regional planning, and the coordinated development between regional economy and power grid. This paper presented the stages division theory of load development based on improved Logistic model, proposed a new definition and meaning for saturated load, and amended and improved the quantified index system for judging power saturated load. Finally, the improved Logistic model was applied to study and analyze the case, the prediction and analysis work of the power saturation scale and saturation time point in the case was completed, and its feasibility was validated.

saturated load; stages division theory; quantified index system; improved Logistic model

国家自然科学基金项目(51261130473 )。

TM 714

A

1000-7229(2015)10-0105-06

10.3969/j.issn.1000-7229.2015.10.016

2015-07-12

2015-09-02

张帆(1982)，男，硕士，高级工程师，研究方向为电力系统自动化；

刘杰锋(1988)，男，硕士，研究方向为电力系统经济性评估、电力负荷预测等；

李冰(1980)，男，硕士，高级工程师，研究方向为电力系统自动化；

陈纲亮(1989)，男，硕士，研究方向为GIS绝缘特性、电力系统自动化；

季节(1989)，女，硕士，研究方向为电力系统规划与可靠性；

徐康泰(1990)，男，硕士研究生，研究方向为电力系统自动化。

Project supported by National Science Foundation of China (51261130473).